밴드갭

Band gap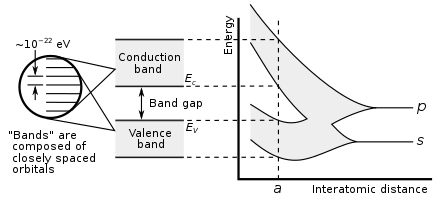
이 기사는 고체 물리학에 관한 것입니다.전자 장치의 전압 제어 회로에 대해서는 밴드갭 전압 참조를 참조하십시오.
이 기사는 반도체에서 발견되는 전자 밴드갭에 대한 것입니다.포토닉 밴드 갭에 대해서는 포토닉 결정을 참조해 주세요.
많은 탄소 원자가 다이아몬드 결정을 형성하기 위해 결합되는 가상 사례에서 전자 밴드 구조가 어떻게 발생하는지 보여줍니다.그래프(오른쪽)는 에너지 수준을 원자 간 간격의 함수로 나타냅니다.원자가 멀리 떨어져 있을 때(그래프의 오른쪽) 각 원자는 같은 에너지를 가진 원자가 원자 궤도 p와 s를 가진다.그러나 원자들이 서로 가까워지면 궤도가 겹치기 시작한다.결정에서 N개의 원자의 궤도 교배를 설명하는 블로흐의 정리 때문에, 같은 에너지의 N개의 원자 궤도는 각각 다른 에너지를 가진 N개의 분자 궤도로 분할된다.N은 매우 큰 수이기 때문에 인접한 궤도는 에너지가 매우 가깝기 때문에 연속적인 에너지 대역으로 간주할 수 있습니다.a는 다이아몬드의 실제 결정에서 원자 간격입니다.그 간격에서 궤도들은 5.5 eV 밴드 간격을 두고 원자가와 전도 밴드라고 불리는 두 개의 밴드를 형성합니다.상온에서 극소수의 전자가 이 넓은 에너지 격차를 극복하고 전도 전자가 되기 위한 열에너지를 가지고 있기 때문에 다이아몬드는 절연체입니다.같은 결정구조를 가진 실리콘을 유사한 방법으로 처리하면 1.1eV의 밴드갭을 훨씬 작게 만들어 실리콘을 반도체로 만든다.

고체 물리학에서, 에너지 갭이라고도 불리는 밴드 갭은 전자 상태가 존재할 수 없는 고체 내의 에너지 범위입니다.고체의 전자 밴드 구조 그래프에서 밴드 갭은 일반적으로 절연체 및 반도체의 원자가 밴드 상단과 전도 밴드 하단의 에너지 차이(전자 볼트)를 나타낸다.원자에 결합된 원자가 전자를 촉진하여 전도 전자가 되는데 필요한 에너지로 결정 격자 내에서 자유롭게 이동하며 전류를 전도하는 전하 운반체 역할을 한다.그것은 화학에서의 HOMO/LUMO 격차와 밀접한 관련이 있다.만약 원자가 밴드가 완전히 꽉 차 있고 전도 밴드가 완전히 비어 있다면, 이용 가능한 상태가 없기 때문에 전자는 고체 내에서 움직일 수 없습니다.전자가 결정 격자 내에서 자유롭지 않으면 순 전하 캐리어 이동성이 없기 때문에 전류가 발생하지 않습니다.그러나 일부 전자가 원자가 대역(대부분 가득)에서 전도 대역(대부분 비어 있음)으로 이동하면 전류가 흐를 수 있습니다(캐리어 생성 및 재조합 참조).따라서 밴드 갭은 고체의 전기 전도율을 결정하는 주요 요소입니다.밴드 갭이 큰 물질은 일반적으로 절연체이며 밴드 갭이 작은 물질은 반도체이며, 반면 도체는 밴드 갭이 매우 작거나 전혀 없다. 왜냐하면 원자가와 전도 밴드가 겹쳐서 연속적인 밴드를 형성하기 때문이다.

반도체 물리학에서

반도체 밴드 구조.

모든 고체는 고유의 에너지 밴드 구조를 가지고 있습니다.밴드 구조의 이러한 변화는 다양한 재료에서 관찰되는 광범위한 전기적 특성에 기인합니다.치수에 따라 밴드 구조와 분광법이 달라질 수 있습니다.1차원, 2차원,[1] 3차원 등 다양한 유형의 치수가 있습니다.

반도체와 절연체에서는 전자가 다수의 에너지 대역에 한정되어 있으며, 전자가 점유할 수 있는 전자 상태가 없기 때문에 다른 영역에서는 금지되어 있습니다.밴드 갭이란 원자가 밴드의 상단과 전도 밴드의 하단의 에너지 차이를 말합니다.전자는 한 띠에서 다른 띠로 점프할 수 있다.단, 원자가대 전자가 전도대역으로 촉진되기 위해서는 이행에 필요한 최소한의 에너지가 필요하다.이 필요한 에너지는 고체 재료의 본질적인 특성입니다.전자는 포논(열) 또는 광자(빛)를 흡수함으로써 전도 대역으로 점프할 수 있는 충분한 에너지를 얻을 수 있다.

반도체는 중간 크기의 0이 아닌 밴드 갭을 가진 물질로, T=0K에서 절연체 역할을 하지만, 융점 이하 온도에서 전도 대역으로 전자의 열 들뜸을 허용합니다.반대로 밴드갭이 큰 소재는 절연체입니다.도체에서는 원자가와 전도대역이 겹칠 수 있으므로 전자상태의 금지영역과의 밴드갭이 없어진다.

고유 반도체의 전도율은 밴드 갭에 따라 크게 좌우됩니다.전도에 사용할 수 있는 전하 캐리어는 밴드 갭에 걸쳐 들뜨기에 충분한 열에너지를 가진 전자와 들뜨면 남는 전자 구멍뿐입니다.

밴드갭 엔지니어링은 GaAlAs, InGaAs, InAlAs 등 특정 반도체 합금의 조성을 제어해 소재의 밴드갭을 제어하거나 변경하는 공정이다.또한 분자선 에피택시 등의 기술로 번갈아 구성되는 층상 재료를 구성할 수도 있습니다.이 방법들은 헤테로 접합 바이폴라 트랜지스터(HBT), 레이저 다이오드 및 태양 전지의 설계에 활용됩니다.

반도체와 절연체의 구별은 관습의 문제이다.하나의 접근법은 반도체를 좁은 밴드 갭을 가진 절연체의 한 종류로 생각하는 것이다.일반적으로 4eV보다 [2]큰 밴드 갭을 갖는 절연체는 반도체로 간주되지 않으며 일반적으로 실제 조건에서 반도체 거동을 보이지 않는다.전자 이동성은 물질의 비공식 분류를 결정하는 역할도 한다.

반도체의 밴드갭 에너지는 온도가 올라갈수록 감소하는 경향이 있다.온도가 상승하면 원자 진동의 진폭이 증가하여 원자간 간격이 커집니다.격자 포논과 자유 전자 및 홀 사이의 상호작용은 또한 밴드 갭에 더 작은 [3]정도로 영향을 미칠 것입니다.밴드 갭 에너지와 온도 사이의 관계는 Varshni의 경험적 표현(Y. P. Varshni의 이름을 딴 것)으로 설명할 수 있다.

{\ T 여기서g E(0), α 및 β는 물질 [4]상수이다.

또한 온도 상승에 따라 격자 진동이 증가하여 전자 산란 효과를 증가시킨다.또한 밴드갭 역치를 넘는 데 필요한 에너지를 가진 캐리어가 많아짐에 따라 반도체 내의 전하 캐리어 수가 증가하므로 온도가 [5]상승함에 따라 반도체 전도율도 증가합니다.

통상적인 반도체 결정에서는 연속적인 에너지 상태에 의해 밴드 갭이 고정된다.양자 닷 결정에서 밴드 갭은 크기에 의존하며 원자가 밴드와 전도 [6]밴드 사이에 에너지 범위를 생성하도록 변경할 수 있다.그것은 양자 구속 효과로도 알려져 있다.

밴드 갭도 압력에 따라 달라집니다.밴드 갭은 재료의 전자 밴드 구조에 따라 직접 또는 간접일 수 있습니다.

앞에서 언급한 바와 같이 치수는 밴드 구조와 분광법이 다르다.1차원인 비금속 고체의 경우 원자가 대역과 전도 대역 사이의 전자적 전이에 따라 달라지는 광학 특성이 있습니다.또한 분광 전이 확률은 최초 궤도 및 최종 궤도 사이이며 [1]적분에 따라 달라진다.θ는i 초기f 궤도, θ는 최종 궤도, θ는f*i 적분, θ는 전기 벡터, u는 쌍극자 [1]모멘트이다.

고체의 2차원 구조는 원자 [1]궤도의 중첩으로 인해 동작한다.가장 단순한 2차원 결정에는 정사각형 [1]격자에 배열된 동일한 원자가 포함되어 있습니다.에너지 분할은 약한 주기적 전위 때문에 1차원 상황에서 Brilouin 구역 가장자리에서 발생하며, 이는 밴드 간 갭을 생성합니다.1차원 상황의 동작은 2차원의 경우 동작의 자유가 추가되기 때문에 발생하지 않는다.또한 2차원 및 3차원 [1]케이스에 대해 강한 주기 전위를 가진 밴드갭을 생성할 수 있다.

직접 및 간접 대역 간격

주요 기사:직접적 및 간접적 대역

소재의 밴드 구조에 근거해, 직접 밴드 갭 또는 간접 밴드 갭이 특징입니다.자유 전자 모델에서 k는 자유 전자의 운동량이며 결정 격자의 주기성을 나타내는 Brilouin 구역 내에서 고유한 값을 가정합니다.재료의 전도대역 중 최저 에너지 상태와 원자가대역의 최고 에너지 상태의 운동량이 같으면 재료는 직접 밴드갭을 가진다.동일하지 않을 경우 재료는 간접적인 밴드 갭을 가지며, 보존을 만족시키기 위해 전자 전이가 운동량 전이를 거쳐야 합니다.이러한 간접적인 "금지된" 전환은 여전히 발생하지만, 매우 낮은 확률과 약한 [7]에너지에서 발생합니다.밴드갭이 직접 있는 재료는 밴드갭보다 에너지가 큰 광자에 의해 원자가 전자를 직접 전도 대역에 들뜨게 할 수 있다.반대로 간접 밴드 갭이 있는 물질의 경우, 광자와 포논은 모두 운동량 변화를 수반하는 원자가 밴드 상단에서 전도 밴드 하단으로의 전환에 관여해야 한다.따라서 다이렉트 밴드갭 재료는 발광 및 흡수 특성이 강하며 태양광 발전(PV), 발광 다이오드(LED) 및 레이저 다이오드에 더 적합한 경향이 있지만 간접 밴드갭 재료는 다른 유리한 특성을 가진 경우 PV 및 LED에 자주 사용됩니다.

발광 다이오드 및 레이저 다이오드

주요 기사:발광 다이오드

LED와 레이저 다이오드는 일반적으로 광자를 발생원 반도체 재료의 밴드 간격에 가깝고 약간 큰 에너지로 방출합니다.따라서 밴드 갭 에너지가 증가함에 따라 LED 또는 레이저 색상은 적외선에서 빨간색으로, 무지개를 통해 보라색, 그리고 [8]UV로 바뀝니다.

광전지

주요 기사:태양전지
쇼클리-퀴저 한계는 반도체 밴드 갭의 함수로서 무농축 태양광 하에서 단일 접합 태양 전지의 최대 효율을 제공한다.밴드 갭이 너무 높으면 대부분의 주간 광자는 흡수될 수 없습니다. 너무 낮으면 대부분의 광자는 밴드 갭을 가로질러 전자를 자극하는 데 필요한 것보다 훨씬 더 많은 에너지를 가지고 나머지는 낭비됩니다.상용 태양 전지에 일반적으로 사용되는 반도체는 실리콘(1.1eV) 또는 CdTe(1.5eV)와 같이 이 곡선의 피크 부근에 밴드 갭이 있습니다.쇼클리-퀴저 한계는 탠덤 태양전지를 만들기 위해 서로 다른 밴드 갭 에너지를 가진 물질을 결합함으로써 실험적으로 초과되었다.

광대역 간격(아래 참조)은 태양전지가 [9]흡수하는 태양 스펙트럼의 부분을 결정합니다.반도체는 밴드갭보다 작은 에너지의 광자를 흡수하지 않으며, 광자에 의해 생성되는 전자-공 쌍의 에너지는 밴드갭 에너지와 같다.발광매체를 이용하여 밴드갭 이상의 에너지를 가진 광자를 태양전지를 [10]포함한 반도체의 밴드갭에 가까운 광자 에너지로 다운컨버전트한다.

밴드 갭 리스트

선택한 일부 재료의 밴드 갭 값은 다음과 같습니다.반도체의 밴드 간격에 대한 포괄적인 목록은 반도체 재료 목록을 참조하십시오.

그룹. 재료. 기호. 302K에서의 밴드갭(eV) 언급
III-V 질화 알루미늄 에이엔 6.0 [11]
IV 다이아몬드 C 5.5 [12]
IV 실리콘 시 1.14 [13]
IV 게르마늄 ge 0.67 [13]
III-V 질화 갈륨 GaN 3.4 [13]
III-V 인화 갈륨 GaP 2.26 [13]
III-V 비화 갈륨 GaAs 1.43 [13]
IV-V 질화 규소 Si3N4 5 [14]
IV-VI 황화납(II) PBS 0.37 [13]
IV-VI 이산화규소 SiO2 9 [15]
산화구리(I) Cu2O 2.1 [16]

광밴드갭과 전자밴드갭

큰 들뜸 결합 에너지를 가진 물질에서, 광자는 들뜸(결합 전자-공 쌍)을 만들기에 겨우 충분한 에너지를 가질 수 있지만, 전자와 홀(서로 전기적으로 끌리는 것)을 분리하기에 충분한 에너지를 가질 수 없다.이 상황에서는 '광대역 간격'과 '전자대역 간격'(또는 '수송 간격')이 구분됩니다.광학 밴드갭은 광자가 흡수되는 역치이며, 전송 간격은 함께 결합되지 않은 전자-공 쌍을 생성하기 위한 역치이다.광밴드갭은 트랜스포트갭보다 낮은 에너지입니다.

실리콘, 비화갈륨 등 거의 모든 무기반도체에서는 전자와 홀(여기에너지가 매우 작음)의 상호작용이 거의 없기 때문에 광밴드갭과 전자밴드갭은 기본적으로 동일하며 이들 간의 구별은 무시된다.그러나 유기 반도체 및 단벽 카본 나노튜브를 포함한 일부 시스템에서는 이러한 차이가 유의할 수 있습니다.

다른 준입자에 대한 밴드 간격

광자학에서 대역 간격 또는 정지 대역은 터널링 효과가 무시될 경우 물질을 통해 광자를 전송할 수 없는 광자 주파수 범위이다.이러한 거동을 나타내는 물질을 포토닉 결정이라고 합니다.초균일성의[17] 개념은 포토닉 결정의 범위를 넘어 포토닉 밴드 갭 소재의 범위를 넓혔다.이 기술을 초대칭 양자역학에서 적용함으로써 결정이나 준결정과 완전히 동등한 밴드 갭을 지원하는 새로운 종류의 광학 무질서 물질이 [18]제안되었다.

비슷한 물리학이 포논 [19]결정의 포논에도 적용된다.

자재

전자제품 토픽 목록

「 」를 참조해 주세요.

레퍼런스

  1. ^ a b c d e f Cox, P.A. (1987). The Electronic Structure and Chemistry of Solids. pp. 102–114.
  2. ^ Babu, V. Suresh (2010). Solid State Devices and Technology, 3rd Edition. Peason.
  3. ^ Ünlü, Hilmi (September 1992). "A thermodynamic model for determining pressure and temperature effects on the bandgap energies and other properties of some semiconductors". Solid-State Electronics. 35 (9): 1343–1352. Bibcode:1992SSEle..35.1343U. doi:10.1016/0038-1101(92)90170-H.
  4. ^ Varshni, Y.P. (January 1967). "Temperature dependence of the energy gap in semiconductors". Physica. 34 (1): 149–154. Bibcode:1967Phy....34..149V. doi:10.1016/0031-8914(67)90062-6.
  5. ^ Cox, P. A. (1987). The electronic structure and chemistry of solids. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-855204-1. OCLC 14213060.
  6. ^ 「Evident Technologies」2009-02-06년 Wayback Machine에 아카이브.Evidenttech.com 를 참조해 주세요.2013-04-03에 취득.
  7. ^ Cox, P. A. (1987). The electronic structure and chemistry of solids. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-855204-1. OCLC 14213060.
  8. ^ Dean, K J (August 1984). "Waves and Fields in Optoelectronics: Prentice-Hall Series in Solid State Physical Electronics". Physics Bulletin. 35 (8): 339. doi:10.1088/0031-9112/35/8/023.
  9. ^ 나노스케일 재료 설계.Nrel.gov 를 참조해 주세요.2013-04-03에 취득.
  10. ^ 나노 결정 발광 태양 변환기, 2004
  11. ^ Feneberg, Martin; Leute, Robert A. R.; Neuschl, Benjamin; Thonke, Klaus; Bickermann, Matthias (16 August 2010). "High-excitation and high-resolution photoluminescence spectra of bulk AlN". Physical Review B. 82 (7): 075208. Bibcode:2010PhRvB..82g5208F. doi:10.1103/PhysRevB.82.075208.
  12. ^ Kittel, Charles. Introduction to Solid State Physics, 7th Edition. Wiley.
  13. ^ a b c d e f Streetman, Ben G.; Sanjay Banerjee (2000). Solid State electronic Devices (5th ed.). New Jersey: Prentice Hall. p. 524. ISBN 0-13-025538-6.
  14. ^ Bauer, J. (1977). "Optical properties, band gap, and surface roughness of Si3N4". Physica status solidi (a). 39 (2): 411–418.
  15. ^ Vella, E.; Messina, F.; Cannas, M.; Boscaino, R. (2011). "Unraveling exciton dynamics in amorphous silicon dioxide: Interpretation of the optical features from 8 to 11 eV". Physical Review B. 83 (17): 174201. Bibcode:2011PhRvB..83q4201V. doi:10.1103/PhysRevB.83.174201.
  16. ^ Baumeister, P.W. (1961). "Optical Absorption of Cuprous Oxide". Physical Review. 121 (2): 359. Bibcode:1961PhRv..121..359B. doi:10.1103/PhysRev.121.359.
  17. ^ Xie, R.; Long, G. G.; Weigand, S. J.; Moss, S. C.; Carvalho, T.; Roorda, S.; Hejna, M.; Torquato, S.; Steinhardt, P. J. (29 July 2013). "Hyperuniformity in amorphous silicon based on the measurement of the infinite-wavelength limit of the structure factor". Proceedings of the National Academy of Sciences. 110 (33): 13250–13254. Bibcode:2013PNAS..11013250X. doi:10.1073/pnas.1220106110. PMC 3746861. PMID 23898166.
  18. ^ Yu, Sunkyu; Piao, Xianji; Hong, Jiho; Park, Namkyoo (16 September 2015). "Bloch-like waves in random-walk potentials based on supersymmetry". Nature Communications. 6 (1): 8269. arXiv:1501.02591. Bibcode:2015NatCo...6E8269Y. doi:10.1038/ncomms9269. PMC 4595658. PMID 26373616.
  19. ^ Eichenfield, Matt; Chan, Jasper; Camacho, Ryan M.; Vahala, Kerry J.; Painter, Oskar (2009). "Optomechanical crystals". Nature. 462 (7269): 78–82. arXiv:0906.1236. Bibcode:2009Natur.462...78E. doi:10.1038/nature08524. ISSN 0028-0836. PMID 19838165. S2CID 4404647.

외부 링크