아핀 리 대수

수학에서 아핀 리 대수학은 무한차원 리 대수학으로 유한차원 단순 리 대수학에서 표준적인 방식으로 구성된다.일반화된 카르탄 행렬이 양의 반확정성이며 코랭크 1을 갖는 Kac-Moody 대수다.순전히 수학적인 관점에서 보면, 그들의 대표이론이 유한차원 반실현 리알헤브라의 대표이론과 마찬가지로 일반 카크-무디 알헤브라의 대표이론보다 훨씬 잘 이해되기 때문에 흥미롭다.빅터 칵이 관찰한 바와 같이, 아핀 리 알헤브라의 표현을 위한 캐릭터 공식은 특정한 결합적 정체성, 즉 맥도날드의 정체성을 내포하고 있다.

아핀 리 알헤브라는 구성된 방식 때문에 끈 이론과 2차원 순응장 이론에서 중요한 역할을 한다: 간단한 리 ${\mathfrak {g}}$ g ${\$ 부터 ${\mathfrak {g}}$ g ${\$ L ${\matfrak{g$ ${\mathfrak {g}}$ ${\$ { $mat$ 에 의해 형성된 루프 대수 L g { $L{\mathfrak {g}}$ {g}을 고려한다. $hfrak{g}}$ - 포인트와이즈 정류자가 있는 원(닫힌 문자열로 표시됨)에서 함수를 ${\mathfrak {g}}$ 계산한다.appine ${\hat {\mathfrak {g}}}$ 대수 g ${\hat {\mathfrak {g}}}$ {\ $displaystyle {\hat$ {\ $mathfrak{$ g}}}}는 루프 대수에서 1개의 치수를 더하고 비삼차적인 방법으로 정류자를 수정하여 얻어지는데 ${\hat {\mathfrak {g}}}$ , 물리학자들은 양자 이상(이 경우 WZW 모델의 이상)을 중심 확장이라고 부른다.More generally, if σ is an automorphism of the simple Lie algebra ${\mathfrak {g}}$ associated to an automorphism of its Dynkin diagram, the twisted loop algebra $L_{\sigma }{\mathfrak {g}}$ consists of ${\mathfrak {g}}$ -valued functions f on the real line비틀린 주기성 조건 $f (x$ + $2π)$ = σ $f (x$ )를 만족한다 $.$ 그들의 중심 확장자는 정확히 뒤틀린 아핀 리 알헤브라스다.끈 이론의 관점은 모듈형 그룹 아래에서 그들의 표현 문자들이 그들 사이에서 변화한다는 사실처럼 아핀 리 알헤브라의 많은 깊은 속성을 이해하는 데 도움이 된다.

단순한 리알헤브라의 아핀 리알헤브라스

정의

${\mathfrak {g}}$ ${\$ 이 ${\mathfrak {g}}$ (가) 유한차원 단순 Lie 대수학인 경우 해당 appine ${\hat {\mathfrak {g}}}$ 대수 g ${\hat {\mathfrak {g}}}$ 은(는) ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$ Lie 대수 g ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$ ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$ ${\mathfrak {g}}\otimes \mathbb {\mathbb {C} } [t,t^{-1}]$ - $]{\displaystyle {g\otimes \maths \mathb$ }의 중심 확장자로 구성된다 ${\hat {\mathfrak {g}}}$ . $b$ 1차원 $중심$ $\mathbb {\mathbb {C} } c.$ 를 가진 ${\$ mathb { $C}$ [ $t,t^{-$ 1}]}, 1차원 중심 C $.$ {\ $displaystyle$ \ $mathb {\mathb {\c}$ c $.}$ 벡터 공간으로서 $\mathbb {\mathbb {C} } c.$ ,

{\widehat {g}={\mathfrak {g}}\mathb {\mathb {C}}}[t,t^{-1}]\oplus \mathb {\c}c,

여기서 $\mathbb {\mathbb {C} } [t,t^{-1}]$ [ $\mathbb {\mathbb {C} } [t,t^{-1}]$ , t $\mathbb {\mathbb {C} } [t,t^{-1}]$ - $\mathbb {\mathbb {C} } [t,t^{-1}]$ $\mathbb {\mathbb {C} } [t,t^{-1}]$ $\mathb {\mathb {C}}$ { $t,t^{-1}}}$ 은(는) 불확정 t에 있는 Laurent 다항식의 복합 벡터 공간이다 $\mathbb {\mathbb {C} } [t,t^{-1}]$ .Lie Bracket은 공식에 의해 정의된다.

[a\otimes t^{n}+\b\otimes t^{m}+\c]=[a,b]\otimes t^{n+m}+\langle n\c}b\angle n\n\n,0}c

for all $a,b\in {\mathfrak {g}},\alpha ,\beta \in \mathbb {\mathbb {C} }$ and $n,m\in \mathbb {Z}$ , where $[a,b]$ is the Lie bracket in the Lie algebra ${\mathfrak {g}}$ and ${\display$ $스타일 \langle \cdot \cdot \rangle$ }은 $\langle\cdot |\cdot\rangle$ $($ 는) ${\mathfrak {g}}.$ ${\displaystyle$ {\ $mathfrak {g}$ 의 Cartan-Killing 양식이다. $}$

유한차원 반실행 리 대수에 해당하는 아핀 리 대수학은 그 단순한 합계에 해당하는 아핀 리 알헤브라의 직접 합이다.정의한 아핀 리 대수학에는 구별되는 파생어가 있다.

\cHB(a\otime t^{m}+\c)=t{d \over dt}(a\otime t^{m}).

해당 아핀 Kac-Moody 대수학은 [d, A] = Δ(A)를 만족하는 추가 발생기 d를 추가하여 반간접 생산물로 정의된다.

Dynkin 다이어그램 구성

각 부속 리 대수학의 Dynkin 도표는 해당 단순 리 대수+상상의 루트의 추가에 해당하는 추가 노드의 그것들로 구성된다.물론 그러한 노드는 어떤 위치에서도 Dynkin 다이어그램에 부착될 수 없지만, 각각의 간단한 Lie 대수에는 Lie 대수 외부 자동화 그룹의 카디널리티와 동일한 다수의 가능한 부착물이 존재한다.특히 이 집단은 항상 정체성 요소를 포함하고 있으며, 이에 상응하는 어핀 리 대수학(Affinine Lie 대수학)을 언스트어핀 리 대수학(unwistered appendine Lie 대수학이라고 부른다.단순 대수학에서 내부 자동화가 아닌 자동화를 인정할 때, 다른 Dynkin 도표를 얻을 수 있으며 이는 뒤틀린 아핀 리알헤브라와 일치한다.

아핀 리알헤브라를 위한 Dynkin 도표

노드가 녹색으로 추가된 확장(부속되지 않은) 연결 Dynkin 다이어그램 세트	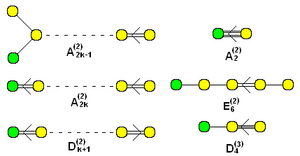"뒤틀린" 부속서식은 (2) 또는 (3) 위첨자로 이름 지어진다. (k는 그래프에서 노드 수입니다.)

중앙 확장자 분류

해당 단순 Lie 대수학의 Dynkin 다이어그램에 추가 노드를 부착하는 것은 다음과 같은 구조에 해당한다.appine Lie 대수학은 항상 해당 간단한 Lie 대수학의 루프 대수학의 중심 확장자로 구성될 수 있다.만약 사람이 대신 반이행 리 대수학으로 시작하기를 원한다면, 반이행 대수학의 단순 요소 수와 동일한 수의 원소를 중심으로 확장할 필요가 있다.물리학에서는 흔히 반이행 대수학 및 아벨리아 $\mathbb {\mathbb {C} } ^{n}$ $\mathbb {\mathbb {C} } ^{n}$ n ${\$ mathb {\ $mathb{C} ^n}}$ 을(를) 대신 고려한다 $\mathbb {\mathbb {C} } ^{n}$ 이 경우 n 아벨리아 발전기를 위한 중심 원소 n개를 더 추가해야 한다.

해당 단순 콤팩트 리 그룹의 루프 그룹의 두 번째 일체형 코호몰로지 정수에 이형성이 있다.단일 발전기에 의한 아핀 리 그룹의 중앙 확장부는 위상학적으로 이 자유 루프 그룹 위에 원 모양의 묶음으로, 진동의 첫 번째 체르누스 등급으로 알려진 2등급에 의해 분류된다.따라서 아핀 리 그룹의 중심연장은 물리학 문헌에서 처음으로 나타난 레벨이라고 하는 단일 파라미터 k로 분류된다.아핀 콤팩트 그룹의 단일 최고 중량 표현은 k가 자연수일 때만 존재한다.보다 일반적으로, 반단순 대수학을 고려한다면, 각 단순 요소에는 중심 전하가 있다.

표현 이론

appine Lie Algebras의 표현 이론은 보통 Verma 모듈을 사용하여 개발된다.반단순 리알헤브라의 경우와 마찬가지로, 이것들은 가장 높은 무게의 모듈로서 얻을 수 있다.유한차원 표현은 없다; 이는 유한차원 Verma 모듈의 null 벡터가 반드시 0인 반면, appine Lie Algebras의 경우는 그렇지 않다.대략적으로 말하면 킬링 폼이 $c,\delta$ , $c,\delta$ ${\displaystyle$ c $,\delta }$ 방향으로 $c,\delta$ 로렌츠어이므로 ( $z$ $(z,{\bar {z}})$ z $){\bar$ { $z}}}$ 은 문자열에서 "라이트콘 좌표"라고 부르기도 $(z,{\bar {z}})$ 한다."방사적으로 주문한" 현재 연산자 제품은 $z=\exp(\tau +i\sigma )$ 세계시트를 따라 시간과 $\tau$ 같은 방향과 $\tau$ $\sigma$ $z=\exp(\tau +i\sigma )$ ${\displaystyle$ z $=\exp$ ( $z=\exp(\tau +i\sigma )$ + $z=\exp(\tau +i\sigma )$ $\tau$ $z=\exp(\tau +i\sigma )$ $){\displaystyle$ z=\exp $(\tau +i\sigma$ $)}}}$ 을 $z=\exp(\tau + i\sigma)$ $\sigma$ (를) 따라 시간적 방향과 ordered ${\displaysty$ \sigmairon \sigmautiform \ $sigma$ \sigmaut)을 취하여 정상으로 주문된 것으로 이해할 수 있다.

웨일 그룹 및 캐릭터

아핀 리 대수학의 웨일 그룹은 제로 모드 대수(루프 대수학을 정의하는 데 사용되는 리 대수)와 코루트 격자(Coroot lattice)의 웨일 그룹의 반직접 생산물로 쓸 수 있다.

아핀 리 알헤브라의 대수적 문자의 웨일 문자 공식은 웨일-카크 문자 공식에 일반화된다.이것들로부터 많은 흥미로운 건설들이 뒤따른다.자코비 세타 함수의 일반화를 구성할 수도 있다.이러한 세타 함수는 모듈형 그룹에서 변한다.반단순 리알헤브라의 일반적인 분모 정체성 또한 일반화된다; 등장인물들은 가장 높은 가중치의 "변형"이나 q-아날로그로 쓰여질 수 있기 때문에, 이것은 많은 새로운 결합 정체성을 디데킨드 에타 함수에 대해 이전에 알려지지 않았던 많은 정체성을 포함한다.이러한 일반화는 랭글랜드 프로그램의 실질적인 예로 볼 수 있다.

적용들

스가와라 건설로 인해 어떤 아핀 리 대수학의 보편적 포락 대수학에는 아발지브라로서 비라소로 대수학(Virasoro 대수학)이 있다.이로써 아핀 리알헤브라는 WZW 모델이나 코제트 모델과 같은 정합적 필드 이론의 대칭 알헤브라의 역할을 할 수 있게 되었다.그 결과 끈 이론에 대한 세계 시트의 설명에도 아핀 리알헤브라가 등장한다.

참조

Di Francesco, P.; Mathieu, P.; Sénéchal, D. (1997), Conformal Field Theory, Springer-Verlag, ISBN 0-387-94785-X
Fuchs, Jurgen (1992), Affine Lie Algebras and Quantum Groups, Cambridge University Press, ISBN 0-521-48412-X
Goddard, Peter; Olive, David (1988), Kac-Moody and Virasoro algebras: A Reprint Volume for Physicists, Advanced Series in Mathematical Physics, vol. 3, World Scientific, ISBN 9971-5-0419-7
Kac, Victor (1990), Infinite dimensional Lie algebras (3 ed.), Cambridge University Press, ISBN 0-521-46693-8
Kohno, Toshitake (1998), Conformal Field Theory and Topology, American Mathematical Society, ISBN 0-8218-2130-X
Pressley, Andrew; Segal, Graeme (1986), Loop groups, Oxford University Press, ISBN 0-19-853535-X

Search