6데미큐브

데미헥세락트 (6데미큐브)
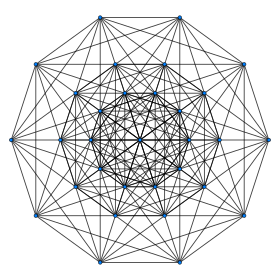페트리 폴리곤 투영
유형	제복6폴리토프
가족	데미하이퍼큐브
슐레플리 기호	{3,3^3,1} = h{4,3⁴} s{2^1,1,1,1,1}
콕시터 도표	= =
콕시터 기호	1₃₁
5시 15분	44	12 {3^1,2,1} 32 {3⁴}
4시 15분	252	60 {3^1,1,1} 192 {3³}
세포	640	160 {3^1,0,1} 480 {3,3}
얼굴	640	{3}
가장자리	240
정점	32
정점수	수정 5-단순
대칭군	D₆, [3^3,1,1] = [1⁺,4,3⁴] [2⁵]⁺
페트리 폴리곤	데카곤
특성.	볼록하게 하다

기하학에서 6데미큐브 또는 데미헥터랙트는 정점이 번갈아 제거된 6-큐브(헥서락트)로 구성된 균일한 6-폴리토프다. 그것은 demihpercube라고 불리는 균일한 폴리토페스로 이루어진 치수 무한의 가족의 일부분이다.

E. L. Elte는 1912년에 그것을 반정형 폴리토프로 확인하였고, 6차원 반정도의 폴리토프에 대해 HM으로₆ 표기하였다.

Coxeter named this polytope as 1₃₁ from its Coxeter diagram, with a ring on one of the 1-length branches, . It can named similarly by a 3-dimensional exponential Schläfli symbol $\left\{3{\begin{array}{l}3,3,3\\3\end{array}}\right\}$ or {3,3^3,1}.

데카르트 좌표, 평행 좌표.

원점에 중심을 둔 데미헥세락트의 정점에 대한 데카르트 좌표는 16진법의 반이다.

(±1,±1,±1,±1,±1,±1)

더하기 기호가 홀수인 채로

구성으로

이 구성 매트릭스는 6-demicube를 나타낸다. 행과 열은 꼭지점, 가장자리, 면, 셀, 4-패스 및 5-패스에 해당한다. 대각선 숫자는 6데미큐브 전체에서 각 원소가 얼마나 많이 발생하는지 알려준다. 비대각 숫자는 열의 요소 중 몇 개가 행의 요소 안에서 또는 열 요소에서 발생하는지 알려준다.^[1]^[2]

대각선 f-벡터 번호는 Wythoff 구조를 통해 도출되며, 한 번에 하나의 거울을 제거하여 서브그룹 주문의 전체 그룹 순서를 나눈다.^[3]

D₆	k-face	f_k	f₀	f₁	f₂	f₃		f₄		f₅		크-피규격	메모들
A을₄	( )	f₀	32	15	60	20	60	15	30	6	6	r{3,3,3}	D₆/A₄ = 32*6!/5! = 32
A₃A₁A₁	{ }	f₁	2	240	8	4	12	6	8	4	2	{}x{3,3}	D₆/AAA₃₁₁ = 32*6!/4!/2/240
A₃A₂	{3}	f₂	3	3	640	1	3	3	3	3	1	{3}v( )	D₆/A₃A₂ = 32*6!/4!/3! = 640
A₃A₁	h{4,3}	f₃	4	6	4	160	*	3	0	3	0	{3}	D₆/A₃A₁ = 32*6!/4!/2 = 160
A₃A₂	{3,3}	f₃	4	6	4	*	480	1	2	2	1	{}v( )	D₆/A₃A₂ = 32*6!/4!/3! = 480
D₄A₁	h{4,3,3}	f₄	8	24	32	8	8	60	*	2	0	{ }	D₆/D₄A₁ = 32*6!/8/4!/2 = 60
A을₄	{3,3,3}	f₄	5	10	10	0	5	*	192	1	1	{ }	D₆/A₄ = 32*6!/5! = 192
D₅	h{4,3,3}	f₅	16	80	160	40	80	10	16	12	*	( )	D₆/D₅ = 32*6!/16/5! = 12
A을₅	{3,3,3,3}	f₅	6	15	20	0	15	0	6	*	32	( )	D₆/A₅ = 32*6!/6! = 32

이미지들

맞춤법 투사
콕시터 평면	B₆
그래프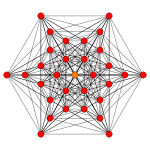
치측 대칭	[12/2]
콕시터 평면	D₆	D₅
그래프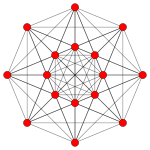
치측 대칭	[10]	[8]
콕시터 평면	D₄	D₃
그래프
치측 대칭	[6]	[4]
콕시터 평면	A을₅	A을₃
그래프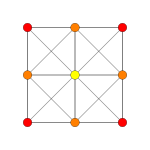
치측 대칭	[6]	[4]

관련 폴리토페스

D₆ 대칭이 있는 47개의 균일한 폴리토프가 있으며, 31개는 B₆ 대칭으로 공유되며, 16개는 고유하다.

6데미큐브, 1은₃₁ 콕시터가 k₃₁ 시리즈로 표현한 균일한 폴리토페의 치수 시리즈 중 3번째다. 다섯 번째 수치는 유클리드 벌집, 셋₃₁, 마지막은 비복합 쌍곡 벌집, 넷이다₃₁. 각 진행성 균일 폴리토프는 정점 모양으로 이전부터 구성된다.

k₃₁ 치수 도형

n	4	5	6	7	8	9
콕시터 무리를 짓다	A₃A₁	A을₅	D₆	E₇	${\tilde {E}}_{7}$ ~ ${\tilde {E}}_{7}$ ${\$ = E₇⁺	${\bar {T}}_{8}$ 8 ${\$ ${\bar {T}}_{8}$ E₇⁺⁺
콕시터 도표를 만들다
대칭	[3^−1,3,1]	[3^0,3,1]	[3^1,3,1]	[3^2,3,1]	[3^3,3,1]	[3^4,3,1]
주문	48	720	23,040	2,903,040	∞
그래프					-	-
이름	−1₃₁	0₃₁	1₃₁	2₃₁	3₃₁	4₃₁

콕시터가 1시리즈로_3k 표현한 균일한 폴리토페스와 허니콤의 치수계열에서도 두 번째다. 네 번째 수치는 유클리드 벌집 1이며₃₃, 마지막은 비복합 쌍곡 벌집 1이다₃₄.

1차원_3k 도형

공간	유한한				유클리드 주	쌍곡선
n	4	5	6	7	8	9
콕시터 무리를 짓다	A₃A₁	A을₅	D₆	E₇	${\tilde {E}}_{7}$ ~ ${\tilde {E}}_{7}$ ${\$ =E₇⁺	${\bar {T}}_{8}$ 8 ${\$ ${\bar {T}}_{8}$ E₇⁺⁺
콕시터 도표를 만들다
대칭	[3^−1,3,1]	[3^0,3,1]	[3^1,3,1]	[3^2,3,1]	[[3^3,3,1]]	[3^4,3,1]
주문	48	720	23,040	2,903,040	∞
그래프					-	-
이름	1_3,-1	1₃₀	1₃₁	1₃₂	1₃₃	1₃₄

꼬치 이코사면체

Coxeter는 12개의 꼭지점의 부분집합을 식별했는데, 이정맥 자체와 대칭은 같지만 각도는 서로 다른 정규 기울기 Icosahedron {3, 5}이다. 그는 이것을 보통 꼬치꼬치 고드름이라고 불렀다.^[4]^[5]

참조

^ Coxeter, 일반 폴리탑, 1.8초 구성
^ Coxeter, 복합 일반 폴리토페스, 페이지 117
^ Klitzing, Richard. "x3o3o *b3o3o3o - hax".
^ Coxeter, H. S. M. The beauty of geometry : twelve essays (Dover ed.). Dover Publications. pp. 450–451. ISBN 9780486409191.
^ Deza, Michael; Shtogrin, Mikhael (2000). "Embedding the graphs of regular tilings and star-honeycombs into the graphs of hypercubes and cubic lattices". Advanced Studies in Pure Mathematics: 77. doi:10.2969/aspm/02710073. Retrieved 4 April 2020.

H.S.M. Coxeter:
- Coxeter, 일반 폴리토페스 (제3판, 1973년), Dover판, ISBN 0-486-61480-8, 페이지 296, 표 I (iii): 일반 폴리토페스, n-dimension(n≥5)의 일반 폴리토페 3개
- H.S.M. Coxeter, 일반 폴리토페스, 제3판, Dover New York, 1973년, 페이지 296, 표 I(iii): 일반 폴리토페스, n-dimension(n≥5)의 일반 폴리토페 3개
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술] Zeit. 46 (1940) 380-407, MR 2,10]
  - (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학] Zeit. 188 (1985) 559-591]
  - (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술] Zeit. 200 (1988) 3-45]
존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장 409장: 헤미큐브: 1_n1)
Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o *b3o3o3o – hax".

외부 링크

Olshevsky, George. "Demihexeract". Glossary for Hyperspace. Archived from the original on 4 February 2007.
다차원 용어집

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A을_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	1₂₂ • 2₂₁
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	1₃₂ • 2₃₁ • 3₂₁
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	1₄₂ • 2₄₁ • 4₂₁
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

[1] Coxeter, 일반 폴리탑, 1.8초 구성

[2] Coxeter, 복합 일반 폴리토페스, 페이지 117

[3] Klitzing, Richard. "x3o3o *b3o3o3o - hax".

[4] Coxeter, H. S. M. The beauty of geometry : twelve essays (Dover ed.). Dover Publications. pp. 450–451. ISBN 9780486409191.

[5] Deza, Michael; Shtogrin, Mikhael (2000). "Embedding the graphs of regular tilings and star-honeycombs into the graphs of hypercubes and cubic lattices". Advanced Studies in Pure Mathematics: 77. doi:10.2969/aspm/02710073. Retrieved 4 April 2020.

[1]

[2]

[3]

[4]

[5]

D6 폴리토페스
h{4,3⁴}	h₂{4,3⁴}	h₃{4,3⁴}	h₄{4,3⁴}	h₅{4,3⁴}	h_2,3{4,3⁴}	h_2,4{4,3⁴}	h_2,5{4,3⁴}
h_3,4{4,3⁴}	h_3,5{4,3⁴}	h_4,5{4,3⁴}	h_2,3,4{4,3⁴}	h_2,3,5{4,3⁴}	h_2,4,5{4,3⁴}	h_3,4,5{4,3⁴}	h_2,3,4,5{4,3⁴}

Search