인공 뉴런

인공뉴런은 신경망인 생물학적 뉴런의 모델로 생각되는 수학적 기능이다.인공 뉴런은 인공 신경망의 ^[1]기본 단위이다.인공 뉴런은 하나 이상의 입력을 받고(신경 수상돌기에서 흥분성 시냅스 후 전위와 억제성 시냅스 후 전위를 나타냄) 출력을 생성하기 위해 그것들을 합산합니다(또는활성화, 축삭을 따라 전달되는 뉴런의 활동 전위를 나타낸다.)보통 각 입력은 개별적으로 가중치가 부여되며, 합계는 활성화 함수 또는 전달^{[clarification needed]} 함수로 알려진 비선형 함수를 통해 전달됩니다.전송 함수는 보통 S자 모양이지만 다른 비선형 함수, 부분 선형 함수 또는 단계 함수의 형태를 취할 수도 있습니다.그것들은 또한 종종 단조롭게 증가하고, 연속적이고, 미분 가능하고, 경계가 있다.많은 작업에서 S자형 및 ReLU와 유사한 활성화 기능을 능가하는 다중 0을 가진 비단조, 무한 및 진동 활성화 기능도 최근에 연구되었다.임계값 기능은 임계값 로직으로 불리는 논리 게이트를 구축하는 데 영감을 주었습니다. 두뇌 프로세싱과 유사한 논리 회로 구축에 적용할 수 있습니다.예를 들어,^[2] 최근 이러한 로직을 개발하기 위해 memristor와 같은 새로운 장치가 광범위하게 사용되고 있습니다.

인공 뉴런 전달 함수는 선형 시스템의 전달 함수와 혼동해서는 안 됩니다.

기본구조

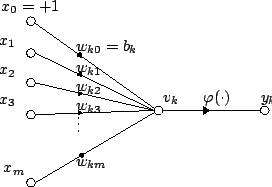
주어진 인공 뉴런 k에 대해 신호 x₀ ~ x와_m 무게_k0 w ~ w를_km 갖는 m + 1 입력이 있다고 가정한다.일반적으로₀ x 입력에는 +1 값이 할당되어 w = b인_k0k 바이어스 입력이 됩니다.이렇게 하면 x에서₁ x까지의_m m개의 실제 입력만 뉴런에 남습니다.

k번째 뉴런의 출력은 다음과 같습니다.

${\displaystyle y_{k}=\varphi \left(\sum _{j=0}^{m}w_{kj}x_{j}\right)}$

$여기$서 ${\\displaystyle \varphi }($phi)는 전송 함수(일반적으로 임계값 함수)입니다.

출력은 생물학적 뉴런의 축삭과 유사하며, 그 값은 시냅스를 통해 다음 층의 입력으로 전파됩니다.또, 출력 벡터의 일부로서 시스템을 빠져나갈 수도 있습니다.

학습 과정 자체가 없습니다.전달함수의 가중치를 계산하고 임계값을 미리 정한다.

종류들

사용된 특정 모델에 따라 반선형 단위, Nv 뉴런, 이진 뉴런, 선형 임계값 함수 또는 McCulloch-Pitts(MCP) 뉴런으로 불릴 수 있습니다.

McCulloch-Pitts 모델과 같은 단순한 인공 뉴런은 ^[3]하나 이상의 신경생리학적 관찰을 반영하기 위한 것이기 때문에 때때로 "카리케쳐 모델"로 묘사된다.

이 섹션은 확장해야 합니다.추가해서 도와주시면 됩니다. (2017년 5월)

생물학적 모델

인공 뉴런은 생물학적 뉴런의 측면을 모방하도록 설계되어 있다.그러나 생물학적 신경망과 인공 신경망 사이에는 상당한 성능 차이가 존재한다.특히 XOR 기능을 학습할 수 있는 진동 활성화 기능을 가진 인간 뇌의 단일 생물학적 뉴런이 발견되었다.^[4]그러나 일반적인 S자형 및 ReLU 유사 활성화 기능을 가진 단일 인공 뉴런은 XOR ^[5]기능을 학습할 수 없습니다.

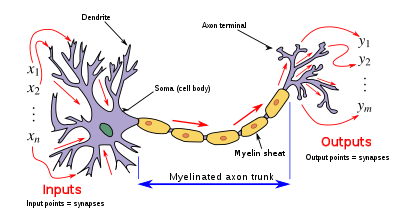
• 수상돌기 – 생물학적 뉴런에서 수상돌기는 입력 벡터 역할을 합니다.이러한 수상돌기는 세포가 많은 수의 인접 뉴런으로부터 신호를 수신할 수 있도록 합니다.위의 수학적 처리와 마찬가지로 각 수상돌기는 수상돌기의 "무게 값"에 의한 "증식"을 수행할 수 있습니다.증식은 시냅스 신경전달물질에 대한 반응으로 덴드라이트에 도입된 신호 화학물질에 대한 시냅스 신경전달물질의 비율을 증가 또는 감소시킴으로써 달성된다.시냅스 신경전달물질의 수신에 응답하여 수상돌기를 따라 신호억제제(즉 반대방향으로 대전된 이온)를 전송함으로써 마이너스 증배효과를 얻을 수 있다.
• 소마 – 생물학적 뉴런에서 소마는 위의 수학적 설명에서 볼 수 있는 합함수 역할을 합니다.덴드라이트로부터 정극 및 음극 신호(각각 들뜸 및 억제)가 소마에 도달하면 세포 체내 용액에 혼합하는 간단한 방법으로 정극 및 음극 이온을 효과적으로 합산하여 첨가한다.
• Axon – Axon은 Soma 내부에서 발생하는 합계 동작으로부터 신호를 받습니다.축삭의 개구부는 기본적으로 소마 내부의 용액의 전위를 샘플링합니다.소마가 특정 전위에 도달하면 축삭은 길이까지 올인 신호 펄스를 전송합니다.이 점에서 축삭은 인공뉴런을 다른 인공뉴런과 연결하는 능력으로 작용한다.

그러나 대부분의 인공 뉴런과 달리 생물학적 뉴런은 분리된 펄스로 발화한다.소마 내부의 전위가 일정한 문턱값에 도달할 때마다 펄스가 축삭을 따라 송신됩니다.이 맥박은 연속값으로 변환할 수 있습니다.축삭이 발사되는 속도(초당 활성화 수 등)는 인접한 셀이 신호 이온을 도입하는 속도로 직접 변환됩니다.생물학적 뉴런이 빠르게 발화할수록, 근처의 뉴런은 더 빨리 전위를 축적합니다(또는 발화한 뉴런에 연결된 수상돌기의 "무게"에 따라 전위를 잃습니다).컴퓨터 과학자와 수학자가 (종종 -1에서 1) 다른 값을 출력할 수 있는 인공 뉴런을 사용하여 생물학적 신경망을 시뮬레이션할 수 있도록 하는 것은 이 변환입니다.

부호화

연구에 따르면 단항 부호화는 새소리 ^[6][7]생성을 담당하는 신경 회로에 사용된다.생물학적 네트워크에서 단항식을 사용하는 것은 아마도 코딩의 고유한 단순성 때문일 것입니다.또 다른 기여 요인은 단항 부호화가 일정 수준의 오류 ^[8]수정을 제공한다는 것입니다.

역사

최초의 인공 뉴런은 워렌 맥컬록과 월터 피트가 1943년에 처음 제안한 임계 논리 단위,^[9] 즉 선형 임계 단위였다.이 모델은 특히 뇌의 ^[10]"신경망"의 계산 모델로서 표적이 되었다.전송 함수로서는 헤비사이드 스텝 함수를 사용하는 것과 동등한 임계값을 사용했습니다.처음에는 이진수 입력과 출력, 가능한 가중치에 대한 몇 가지 제한 및 보다 유연한 임계값이 포함된 단순한 모델만 고려되었다.이러한 디바이스의 네트워크에 의해 부울함수가 실장될 수 있는 것은 처음부터 이미 인식되어 있었기 때문에 AND 및 OR 함수를 실장하여 분리형 또는 접속형 정규형으로 사용할 수 있는 것으로부터 쉽게 알 수 있습니다.또한 연구자들은 뉴런을 통한 피드백을 통해 순환 네트워크가 메모리를 사용하여 동적 시스템을 정의할 수 있다는 것을 곧 깨달았습니다. 그러나 대부분의 연구는 더 작은 난이도로 인해 엄격하게 피드포워드 네트워크에 집중되어 있습니다(그리고 지금도 마찬가지입니다.

선형 역치 함수를 사용한 중요하고 선구적인 인공 신경망은 프랭크 로젠블랫에 의해 개발된 퍼셉트론이었다.이 모델은 이미 뉴런의 보다 유연한 체중 값을 고려했으며 적응 능력이 있는 기계에 사용되었다.역치를 바이어스 항으로 표현하는 것은 1960년 Bernard Widrow에 의해 도입되었다. ADALIN을 참조한다.

1980년대 후반 신경망에 대한 연구가 힘을 되찾으면서 보다 연속적인 형태를 가진 뉴런이 고려되기 시작했다.활성화 함수를 구별할 수 있는 가능성은 체중 조정을 위한 경사 강하 및 기타 최적화 알고리즘을 직접 사용할 수 있게 한다.뉴럴 네트워크는 또한 일반적인 함수 근사 모델로 사용되기 시작했다.역전파라고 불리는 가장 잘 알려진 훈련 알고리즘은 여러 번 재발견되었지만, 그 첫 번째 개발은 폴 ^[11][12]베르보스의 연구로 거슬러 올라간다.

전송 함수의 종류

뉴런의 전달 함수(활성화 함수)는 뉴런을 포함하는 네트워크를 강화하거나 단순화하는 여러 특성을 가지도록 선택된다.결정적으로, 예를 들어, 선형 전송 함수를 사용하는 모든 다층 퍼셉트론은 동등한 단일 계층 네트워크를 가진다.따라서, 다층 네트워크의 이점을 ^{[citation needed]}얻기 위해서는 비선형 함수가 필요하다.

아래에서 u는 모든 경우에 뉴런에 대한 모든 입력의 가중치 합계를 말한다. 즉, n개의 입력에 대해,

${\displaystyle u=\sum _{i=1}^{n}w_{i}x_{i}}$

여기서 w는 시냅스 가중치의 벡터이고 x는 입력의 벡터입니다.

스텝 함수

이 전송 함수의 출력 y는 입력이 지정된 임계값 θ을 충족하는지 여부에 따라 이진수입니다."signal"이 전송됩니다. 즉, 활성화가 임계값을 충족하면 출력이 1로 설정됩니다.

${\displaystyle y=cases}1&{\text{if}}u\theta\0&{\text{if}}u<\theta\end{cases}}}$

이 함수는 퍼셉트론에서 사용되며 다른 많은 모델에 자주 나타납니다.하이퍼플레인으로 입력 공간을 분할합니다.이 기능은 입력의 바이너리 분류를 실행하는 네트워크의 마지막 레이어에서 특히 유용합니다.이는 가중치에 큰 값을 할당함으로써 다른 S자형 함수로부터 근사할 수 있다.

선형 조합

이 경우 출력 단위는 단순히 입력에 바이어스 항을 더한 가중치 합입니다.이러한 다수의 선형 뉴런은 입력 벡터의 선형 변환을 실시한다.이것은 보통 네트워크의 첫 번째 레이어에서 더 유용합니다.고조파 분석과 같은 선형 모델에 기초한 많은 분석 도구가 존재하며, 그것들은 모두 이 선형 뉴런을 가진 신경 네트워크에서 사용될 수 있습니다.바이어스 항을 사용하면 데이터에 아핀 변환을 할 수 있습니다.

참고 항목: 선형 변환, 고조파 분석, 선형 필터, 웨이브릿, 주성분 분석, 독립성분 분석, 디콘볼루션.

S자형

꽤 단순한 비선형 함수인 로지스틱 함수와 같은 Sigmoid 함수도 쉽게 계산되는 도함수를 가지며, 이는 네트워크에서 가중치 업데이트를 계산할 때 중요할 수 있습니다.따라서 네트워크를 보다 쉽게 수학적으로 조작할 수 있게 되어 시뮬레이션의 계산 부하를 최소화해야 하는 초기 컴퓨터 과학자들에게 매력적이었습니다.이전에는 다층 퍼셉트론에서 흔히 볼 수 있었습니다.그러나 최근 연구는 S자형 뉴런이 정류된 선형 뉴런보다 덜 효과적이라는 것을 보여주었다.그 이유는 역전파 알고리즘에 의해 계산된 구배는 활성화가 S자형 뉴런 층을 통해 전파됨에 따라 0을 향해 감소하는 경향이 있으며, S자형 뉴런의 여러 층을 사용하여 신경망을 최적화하는 것이 어렵기 때문이다.

정류기

인공신경망의 맥락에서 정류기는 인수의 양의 부분으로 정의되는 활성화 함수입니다.

${\displaystyle f(x)=x^{+}=\max(0,x),}$

여기서 x는 뉴런에 대한 입력입니다.이것은 램프 기능이라고도 하며 전기 공학 분야의 반파 정류와 유사합니다.이 활성화 함수는 2000년 Hahnloser 등에 의해 강력한 생물학적 동기와 수학적 ^[14]정당성을 가진 Nature 논문에서^[13] 동적 네트워크에 처음 도입되었다.2011년 이전에 널리 사용된 활성화 함수, 즉 로지스틱 Sigmoid(확률 이론에서 영감을 얻은 로지스틱 회귀 참조)와 보다 실용적인^[16] 대응물인 쌍곡선 탄젠트에 비해 더 깊은 네트워크의 ^[15]훈련을 가능하게 하는 것이 2011년에 처음으로 입증되었다.

의사 코드 알고리즘

다음으로 단일 TLU의 단순한 의사 코드 실장을 나타냅니다.부울 입력(true 또는 false)을 받아 활성화 시 단일 부울 출력을 반환합니다.객체 지향 모델이 사용됩니다.여러 가지가 존재하기 때문에 훈련 방법은 정의되어 있지 않습니다.순수하게 기능하는 모델을 사용하는 경우 다음 클래스 TLU는 입력 파라미터 임계값, 가중치 및 부울값을 반환하는 입력을 가진 함수 TLU로 대체됩니다.

클래스 TLU는 다음과 같이 정의된다: 데이터 멤버 임계값: 숫자 데이터 멤버 가중치: 크기 X 함수 멤버 Fire(크기 X의 부란 목록): 부울 정의: 변수 T: 숫자 T ← 0으로 정의된다.1 ~ X의 각 i가 참일 경우 T ← T + 가중치(i) 각 i가 종료되면 끝납니다.f T > threshold를 반환한 후 true를 반환한다.그렇지 않으면 false end를 반환한다.엔드 함수 엔드 클래스의 경우

「 」를 참조해 주세요.

• 결합뉴런
• 연결주의

레퍼런스

추가 정보

외부 링크

• 인간 세포의 기능을 모방하는 인공 [시크]뉴런
• McCulloch-Pitts 뉴런(개요)