곰퍼츠 함수
Gompertz function곰퍼츠 곡선 또는 곰퍼츠 함수는 벤자민 곰퍼츠(1779–1865)의 이름을 딴 시계열 수학 모델의 일종이다. 그것은 특정 기간의 시작과 끝에서 성장이 가장 느린 것으로 묘사되는 S자형 함수다. 함수의 오른쪽 또는 미래 값 점증상은 왼쪽 또는 낮은 값의 점증점보다 곡선에 의해 훨씬 더 점진적으로 접근한다. 이는 두 점근 모두 곡선으로 대칭적으로 접근하는 단순 로지스틱 함수와는 대조적이다. 그것은 일반화된 로지스틱 함수의 특별한 경우다. 이 기능은 원래 인간의 사망률을 설명하기 위해 고안되었지만, 그 이후 생물학에서 적용되도록 수정되었다.
역사
벤자민 곰퍼츠(Benjamin Gompertz, 1779년–1865년)는 런던의 사학자로 사교육을 받은 사람이었다.[1] 그는 1819년에 왕립 협회의 회원으로 선출되었다. 그 기능은 그의 518페이지 하단의 1825년 6월 16일 논문에서 처음 발표되었다.[2] 곰퍼츠 함수는 생명표에서 유의미한 데이터 수집을 단일 함수로 줄였다. 사람이 나이를 먹을수록 사망률이 기하급수적으로 높아진다는 가정에 따른 것이다. 그 결과 곰퍼츠 함수는 특정 연령대에 연령의 함수로 살아가는 개인의 수를 위한 것이다.
1750년대에 프랑스의 수학자 아브라함 드 모이브르(1667–1754)가 사망률의 기능적 모델 구축에 관한 초기 연구가 이루어졌다.[3][4] 그러나 드 모이브르는 사망률이 일정하다고 가정했다. 곰퍼츠의 작품에 대한 연장은 1860년 영국의 악덕사이자 수학자 윌리엄 매튜 메이컴(1826–1891)에 의해 제안되었는데, 그는 곰퍼츠의 기하급수적으로 증가하는 것에 일정한 배경 사망률을 더했다.[5]
공식
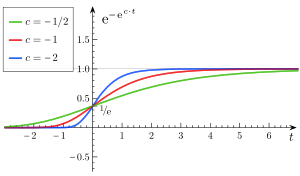
- a는 →- e - - - b- = = ^{
- b x축을 따라 변위를 설정한다(그래프를 왼쪽 또는 오른쪽으로 표시).
- c 증가율 설정(y 스케일링)
- e는 오일러의 번호(e = 2.71828...)
특성.
중간점은 t에 ( t)= / 2 }을를) 풀면 찾을 수 있다.
파생
함수 곡선은 절대 사망률(데케이)이 현재 크기에 따라 기하급수적으로 하락한다는 곰퍼츠 사망률 법칙에서 도출할 수 있다. 수학적으로,
어디에
- = ( ) y( ) 은(는) 성장률이다.
- k는 임의의 상수다.
예제 사용
곰퍼츠 곡선의 사용 예는 다음과 같다.
- 초기에는 비용이 높았던 휴대폰 업테이크(그래서 업테이크 속도가 느렸던 것)가 그 뒤를 이었고, 포화상태에[6] 이르면서 업테이크 속도가 느려진 것이 그 뒤를 이었다.
- 제한된 공간에 있는 인구, 처음에는 출생률이 증가하고 그 다음에는 자원 한계에 도달함에[7] 따라 느려짐
- 종양[8] 성장 모델링
- 금융[9] 및 집계된 하위 국가 대출의 시장 영향을 모델링하는 동적.[10]
- 포식자-선호 관계와 관련하여 맹수 동물에서 개체군 증가를 자세히 설명
- 모집단 내 박테리아 세포 모델링
- 질병 확산 검사
적용들
곰퍼츠 곡선
인구 생물학은 특히 곰퍼츠 함수와 관련이 있다. 이 기능은 특히 특정 유기체 집단의 급속한 성장을 설명하는 동시에 운반 능력이 결정되면 최종 수평 점근증(plateau cell/poption number)도 설명할 수 있는 데 유용하다.
다음과 같이 모델링:
여기서:
- t는 시간이다.
- N은0 세포의 초기 양이다.
- N은I 고원 세포/인구 수이다.
- b는 종양의 초기 성장 속도다.
이러한 고원 세포수의 기능적 고려는 실생활 인구 역학을 정확하게 모방하는데 유용하다. 이 함수는 또한 S자형 함수를 고수하는데, 이는 일반적으로 모집단의 성장을 상세히 기술하는 가장 널리 받아들여지는 관습이다. 게다가 이 기능은 초기 성장률을 이용하는데, 이는 통나무 단계를 거치고 수적으로 빠르게 성장하는 박테리아와 암세포의 개체군에서 흔히 볼 수 있다. 그 인기에도 불구하고, 종양 성장의 함수 초기 속도는 환자에게 존재하는 다양한 미세조직이나 인구 생물학의 경우 다양한 환경적 요인을 고려할 때 예측하기 어렵다. 암 환자의 경우 연령, 식이요법, 민족성, 유전적 전분비, 신진대사, 생활습관, 전이 기원 등의 요인이 종양 성장률을 결정하는 역할을 한다. 운반 능력도 이러한 요인에 따라 변화할 것으로 예상되기 때문에 그러한 현상을 기술하는 것은 어렵다.
대사 곡선
신진대사 기능은 특히 유기체 내의 신진대사 속도에 대한 회계처리와 관련이 있다. 이 기능은 종양 세포를 감시하는 데 적용될 수 있다; 대사율은 역동적이고 매우 유연해서 암의 성장을 자세히 묘사하는데 더 정확하다. 신진대사 곡선은 신체가 조직을 유지하고 만드는 데 제공하는 에너지를 고려한다. 이 에너지는 신진대사로 간주될 수 있으며 세포분열에서 특정한 패턴을 따른다. 에너지 절약은 질량과 개발 시간의 차이와 상관없이 그러한 성장을 모형화하는 데 사용될 수 있다. 모든 세자는 비슷한 성장 패턴을 가지고 있고, 그 결과 이 모델은 종양 발달의 기초인 세포 분열을 고려한다.
- B = 정지 상태에서 에너지 유기체 사용
- NC = 주어진 유기체의 세포 수
- BC= 개별 세포의 대사율
- NBCC= 기존 조직을 유지하는 데 필요한 에너지
- EC= 개별 세포에서 새로운 조직을 만드는 데 필요한 에너지
휴식과 대사율 작업 사이의 차이점은 모델이 성장률을 보다 정확하게 결정할 수 있도록 한다. 휴식의 에너지는 조직을 유지하는 데 사용되는 에너지보다 낮으며, 함께 기존 조직을 유지하는 데 필요한 에너지를 나타낸다. 이 두 가지 요인을 새로운 조직을 만드는 데 필요한 에너지와 함께 사용하면 성장률을 포괄적으로 매핑할 수 있으며, 더욱이 지연 단계를 정확하게 표현할 수 있게 된다.
종양의 성장
1960년대 A.K. Laird는[11] 처음으로 종양의 성장 데이터를 맞추기 위해 곰퍼츠 곡선을 성공적으로 사용했다. 사실 종양은 영양소의 이용가능성이 제한된 밀폐된 공간에서 성장하는 세포군이다. 종양 크기를 X(t)로 나타내면 다음과 같이 곰퍼츠 곡선을 작성하는 것이 유용하다.
여기서:
- X(0)는 시작 관찰 시간에 종양 크기 입니다.
- K는 운반 용량, 즉 사용 가능한 영양소로 도달할 수 있는 최대 크기입니다. 사실 다음과 같다.
X(0)>0에 독립하여 주의할 점은, 치료 등이 없는 경우.. 일반적으로 X(0) < K인 반면, 치료법에서는 X(0) > K일 수 있다.
- α는 세포의 증식 능력과 관련된 상수다.
- 로그는 자연 로그를 가리킨다.
X(t)의 역학은 곰퍼츠 미분방정식에 의해 지배된다는 것을 알 수 있다.
즉, 분해할 때의 형식:
F(X)는 세포 인구의 순간적 증식률로, 세포 인구의 증가에 따른 영양소 경쟁으로 자연이 감소하는 것이 로지스틱 성장률과 유사하다. 그러나 근본적인 차이가 있다: 로지스틱의 경우 소세포 집단의 확산 속도는 유한하다.
곰퍼츠의 경우 확산률은 제한되지 않는다.
Steel과[12] Weldon이 지적한 바와 같이,[13] 세포 인구의 증식률은 궁극적으로 세포분할 시간에 의해 제한된다. 따라서 이는 곰퍼츠 방정식이 작은 종양의 성장을 모형화하는 데 좋지 않다는 증거일 수 있다. 더욱이 최근에는 면역체계와의 상호작용을 포함해 곰퍼츠와 무한 F(0)로 특징지어지는 다른 법칙들이 면역감시의 가능성을 배제한다는 것이 주목되고[14] 있다.
포르날스키 외 연구진의 이론적 연구는 포물선 기능이 더 적절한 초기 단계를 제외하고 암 성장에 대한 곰퍼츠 곡선의 생물물리학적 기초를 보여주었다. 그들은 또한 곰퍼츠 곡선이 광범위한 암 역학 기능 중 가장 전형적인 경우를 묘사하고 있다는 것을 발견했다.
곰퍼츠 성장과 로지스틱 성장
곰퍼츠 미분방정식
일반화된 로지스틱 미분 방정식의 제한 사례
(여기서 > 0 은(는) 양수 이후부터입니다).
또한 일반화된 로지스틱 함수의 그래프에는 다음과 같은 경우 변곡점이 있다.
그리고 곰퍼츠 함수의 그래프에 한 개는
COVID-19 감염 궤적 모델링

리차드 성장 곡선이라고도 불리는 일반화된 로지스틱 함수는 COVID-19 감염 궤적을 모델링하는 데 널리 사용된다.[16] 감염 궤적은 국가, 도시, 주 등과 같은 대상의 누적 감염자 수에 대한 일일 시계열 데이터다. 문헌에는 변형된 재변수가 있다: 자주 사용되는 형태 중 하나는
여기서 , , 3 는 실수이며, 은 양수 실수다. f {\f}의 유연성은 {\\}: (i) 만약 =1 {\ \=1}이면 곡선이 로지스틱 함수로 감소하고, ii 이 0으로 수렴하면 곡선이 곰퍼츠 함수로 수렴되기 때문이다. 역학 모델링에서 },, }}, 는 각각 최종 전염병 크기, 감염률, 지연 단계를 나타낸다. .2) 이) 지정된 경우 검사용 궤적은 오른쪽 패널을 참조하십시오
역학 모델링에서 일반화된 로지스틱 기능과 같은 성장 기능을 사용할 때의 이점 중 하나는 성장 기능을 사용하여 여러 과목(국가, 도시, 주 등)의 감염 궤적을 설명함으로써 다단계 모델 프레임워크로 비교적 쉽게 확장된다는 것이다. 위의 그림을 참조하십시오. 이러한 모델링 프레임워크는 비선형 혼합 효과 모델 또는 계층적 비선형 모델이라고도 한다.
곰프엑스의 성장 법칙
위와 같은 고려사항을 바탕으로 웰던은[13] 곰퍼츠 법칙을 약간 수정하는 곰프-엑스 모델이라 불리는 종양 성장의 수학적 모델을 제안했다. 곰프-Ex 모델에서는 초기에는 자원 경쟁이 없기 때문에 지수법에 따라 세포군이 확장된다고 가정한다. 단, > > 의 경우, 자원 이 가정은 대부분의 시나리오에서 타당하다 그러나 하위 요인 변수를 생성해야 하는 제한 요인의 영향을 받을 수 있다.
성장은 곰퍼츠 법칙을 따른다.
따라서:
X 에 대한 몇 가지 수치 추정치가[13] 있다
- 의 경우 X 9 {\X_{약 10^{
- 약 머린(마우스) 종양의 경우
참고 항목
참조
- ^ Kirkwood, TBL (2015). "Deciphering death: a commentary of Gomperz (1825)'On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies'". Philosophical Transactions of the Royal Society of London B. 370 (1666). doi:10.1098/rstb.2014.0379. PMC 4360127. PMID 25750242.
- ^ Gompertz, Benjamin (1825). "On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies". Philosophical Transactions of the Royal Society of London. 115: 513–585. doi:10.1098/rstl.1825.0026. S2CID 145157003.
- ^ de Moivre, Abraham (1725). Annuities upon Lives …. London, England: Francis Fayram, Benj. Motte, and W. Pearson. 1743년에 제2판이 발행되었고, 1750년에 제3판이 발행되었으며, 1752년에 제4판이 발행되었다.
- ^ Greenwood, M. (1928). "Laws of Mortality from the Biological Point of View". Journal of Hygiene. 28 (3): 267–294. doi:10.1017/S002217240000961X. PMC 2167778. PMID 20475000.
- ^ Makeham, William Matthew (1860). "On the law of mortality and the construction of annuity tables". The Assurance Magazine, and Journal of the Institute of Actuaries. 8 (6): 301–310. doi:10.1017/S204616580000126X.
- ^ Islam T, Fiebig DG, Meade N (2002). "Modelling multinational telecommunications demand with limited data". International Journal of Forecasting. 18 (4): 605–624. doi:10.1016/S0169-2070(02)00073-0.
- ^ Zwietering MH, Jongenburger I, Rombouts FM, van 't Riet K (June 1990). "Modeling of the bacterial growth curve". Applied and Environmental Microbiology. 56 (6): 1875–81. Bibcode:1990ApEnM..56.1875Z. doi:10.1128/AEM.56.6.1875-1881.1990. PMC 184525. PMID 16348228..
- ^ Sottoriva A, Verhoeff JJ, Borovski T, McWeeney SK, Naumov L, Medema JP, et al. (January 2010). "Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity". Cancer Research. 70 (1): 46–56. doi:10.1158/0008-5472.CAN-09-3663. PMID 20048071.
- ^ Caravelli F, Sindoni L, Caccioli F, Ududec C (August 2016). "Optimal growth trajectories with finite carrying capacity". Physical Review E. 94 (2–1): 022315. arXiv:1510.05123. Bibcode:2016PhRvE..94b2315C. doi:10.1103/PhysRevE.94.022315. PMID 27627325. S2CID 35578084..
- ^ Rocha LS, Rocha FS, Souza TT (2017-10-05). "Is the public sector of your country a diffusion borrower? Empirical evidence from Brazil". PLOS ONE. 12 (10): e0185257. arXiv:1604.07782. Bibcode:2017PLoSO..1285257R. doi:10.1371/journal.pone.0185257. PMC 5628819. PMID 28981532.
- ^ Laird AK (September 1964). "Dynamics of Tumor Growth". British Journal of Cancer. 13 (3): 490–502. doi:10.1038/bjc.1964.55. PMC 2071101. PMID 14219541.
- ^ Steel GG (1977). Growth Kinetics of Tumors. Oxford: Clarendon Press. ISBN 0-19-857388-X.
- ^ a b c Wheldon TE (1988). Mathematical Models in Cancer Research. Bristol: Adam Hilger. ISBN 0-85274-291-6.
- ^ d'Onofrio A (2005). "A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences". Physica D. 208 (3–4): 220–235. arXiv:1309.3337. Bibcode:2005PhyD..208..220D. doi:10.1016/j.physd.2005.06.032. S2CID 15031322.
- ^ Fornalski KW, Reszczyńska J, Dobrzyński L, Wysocki P, Janiak MK (2020). "Possible Source of the Gompertz Law of Proliferating Cancer Cells: Mechanistic Modeling of Tumor Growth". Acta Physica Polonica A. 138 (6): 854–862. Bibcode:2020AcPPA.138..854F. doi:10.12693/APhysPolA.138.854.
- ^ Lee, Se Yoon; Lei, Bowen; Mallick, Bani (2020). "Estimation of COVID-19 spread curves integrating global data and borrowing information". PLOS ONE. 15 (7): e0236860. arXiv:2005.00662. Bibcode:2020PLoSO..1536860L. doi:10.1371/journal.pone.0236860. PMC 7390340. PMID 32726361.











 (는) 성장률이다.
(는) 성장률이다.








 (는) 양수 이후부터입니다).
(는) 양수 이후부터입니다). 


![{\displaystyle f(t;\theta _{1},\theta _{2},\theta _{3},\xi )={\frac {\theta _{1}}{[1+\xi \exp(-\theta _{2}\cdot (t-\theta _{3}))]^{1/\xi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29479f9d2bb480d1bf104fc0d84fcbaf00cf99f6)
 실수이며,
실수이며,  양수 실수다.
양수 실수다.  곡선이 로지스틱 함수로 감소하고, ii
곡선이 로지스틱 함수로 감소하고, ii 














