폴리그램(지오메트리)

기하학에서 일반화된 다각형은 폴리그램이라고 할 수 있으며, 특히 그 변수의 수에 의해 이름이 붙여졌다.모든 폴리곤은 폴리그램이지만, 복합 폴리곤이라고 불리는 분리된 가장자리 집합을 포함할 수도 있다.예를 들어 일반 펜타그램인 {5/2}은(는) 5면이고, 일반 육각형인 {6/2} 또는 2{3}은(는) 6면 2개의 삼각형으로 나뉜다.

일반 폴리그램 {p/q}은(는) 일반 항성 폴리곤 집합(gcd(p,q) = 1, q > 1) 또는 일반 폴리곤 화합물 집합(gcd(p,q) > 1)에 있을 수 있다.^[1]

어원

폴리그램 이름은 penta-와 같은 숫자 접두사와 그리스어 접미사 -gram(이 경우 pentram이라는 단어를 생성함)을 결합한다).접두사는 보통 그리스 추기경이지만 다른 접두사를 사용하는 동의어가 존재한다.-gram 접미사는 선을 뜻하는 μαμμῆ(grammos)에서 유래한다.^[2]

일반화된 일반 폴리곤

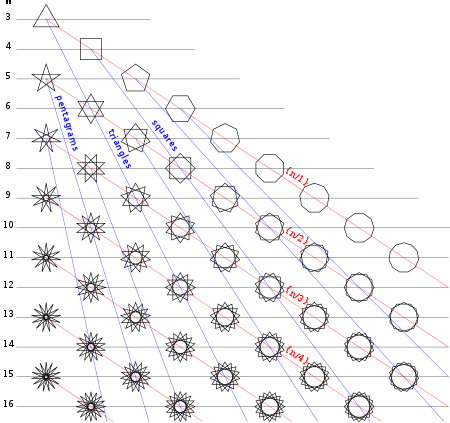
일반 폴리그램은 일반 폴리곤으로서 슐레플리 기호 {p/q}로 표시되며, 여기서 p와 q는 비교적 프라임(인자를 공유하지 않음)과 q q 2로 표시된다.정수 p와 q의 경우, 일정한 간격으로 일정한 간격을 두고 p 포인트의 모든 q번째 점을 연결하여 구성하는 것으로 간주할 수 있다.^[3][1]

{5/2}

{7/2}

{7/3}

{8/3}

{9/2}

{9/4}

{10/3}...

일반 복합 폴리곤

그 밖에 n과 m이 공통인자를 갖는 경우, polygram은 k = gcd(n,m)로 하한 폴리곤, {n/k, m/k}로 해석되며, 회전된 복사본은 복합 폴리곤으로 결합된다.이러한 형상을 일반 복합 다각형이라고 한다.

일부 일반 폴리곤 화합물

삼각형...			제곱...		펜타곤...	펜타그램...
{6/2}=2{3}	{9/3}=3{3}	{12/4}=4{3}	{8/2}=2{4}	{12/3}=3{4}	{10/2}=2{5}	{10/4}=2{5/2}	{15/6}=3{5/2}

참고 항목

• 일반 폴리토페스와 화합물#스타 목록

참조

• 크롬웰, P.; 폴리헤드라, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5. 페이지 175
• 그룬바움, B., G.C.셰퍼드; 틸링 앤 패턴, 뉴욕: W. H. 프리먼 & 코, (1987), ISBN 0-7167-1193-1.
• Grünbaum, B.; 할로우 페이스가 있는 Polyedra, Proc of NATO-ASI on Polytopes... 등 (토론토 1993), Ed T.Bisztriczky 외, Kluwer Academic(1994) 페이지 43–70.
• 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장 404장: 일반 별-폴리토페스 치수 2)
• 현대 순수 기하학에 관한 기초학자인 로버트 라클란.런던: 맥밀런, 1893년, 페이지 83 폴리그램.[1]
• Branko Grünbaum, 폴리곤의 변형, 수학의 가벼운 면: 외젠파워스 기념수학회의 진행과 그 역사