칸막이 함수

수학에서, 그리고 특히 숫자 이론에서, 구분함수는 정수의 구분점과 관련된 산술함수다. 구분 함수라고 할 때, 정수의 구분자 수(1과 숫자 자체를 포함)를 계산한다. 그것은 리만 제타 기능과 아이젠슈타인 모듈형식 시리즈에 관한 관계를 포함한 많은 주목할 만한 정체성에 나타난다. Divisor 함수는 Ramanujan에 의해 연구되었는데, Ramanujan은 여러 가지 중요한 조합과 정체성을 제공했다; 이것들은 Ramanujan의 조항에 따로 다루어져 있다.

관련 함수는 구분함수로서, 명칭이 암시하듯이, 구분함수 위의 합이다.

정의

양수 함수 x(n)의_x 합은 실제 또는 복잡한 수 x에 대해 n의 양수 변수의 x번째 힘의 합으로 정의된다. 다음과 같이 시그마 표기법으로 표현할 수 있다.

${\displaystyle \exma _{x}(n)=\sum _{d\mid n^{x}\,\!}$

여기서 $d{\displaystyle }$ ${\displaystyle \mid n}$ ${\$은 "d dives n"의 속기법이다$$. d(n), ν(n), and(n) 및 τ(n)(독일 테일러 = divisors의 경우)도 σ₀(n) 또는 divisor 수 함수^[1][2](OEIS: A000005)를 나타내는 데 사용된다. x가 1일 때는 시그마 함수 또는 sum of divisors 함수라고 하며 ^[1][3]첨자가 생략되는 경우가 많기 때문에 ((n)은₁ ((n)과 같다(OEIS: A000203).

n의 aliquot s(n)는 적절한 divisor(즉, n 자체를 제외한 divisors, OEIS: A001065), sum(n₁) - n과 같으며, n의 aliquot sum 함수를 반복적으로 적용하여 n의 aliquot sum s(n)을 합한 것이다.

예

예를 들어 σ₀(12)는 12의 구분자 수입니다.

${\displaystyle {\progressed}\ma _{0}(12)&=1^{0}+2^{0}+3^{0}+4^{0}+6^{0}+12^{0}}\\&=1+1+1+1+1+1=6,\end{arged}}}$

σ₁(12)은 모든 구분자의 합계인 반면:

${\displaystyle {\pregated}\ma _{1}(12)&=1^{1}+2^{1}+3^{1}+3^{1}+4^{1}+1}+6^{1}+12^{1}}\\&=1+2+3+4+6+12=28,\end{arged}}}$

적절한 구분자의 고유 합계 s(12)는 다음과 같다.

${\displaystyle {\protected}s(12)&=1^{1}+2^{1}+3^{1}+4^{1}+1}+6^{1}\\&=1+2+3+4+6=16.\end{정렬}}}$

값표

사례 x = 2 ~ 5는 OEIS: A0011157 - OEIS: A001160, x = 6 ~ 24는 OEIS: A013954 - OEIS: A013972에 나열된다.

n	인자화	𝜎0(n)	𝜎1(n)	𝜎2(n)	𝜎3(n)	𝜎4(n)
1	1	1	1	1	1	1
2	2	2	3	5	9	17
3	3	2	4	10	28	82
4	22	3	7	21	73	273
5	5	2	6	26	126	626
6	2×3	4	12	50	252	1394
7	7	2	8	50	344	2402
8	23	4	15	85	585	4369
9	32	3	13	91	757	6643
10	2×5	4	18	130	1134	10642
11	11	2	12	122	1332	14642
12	22×3	6	28	210	2044	22386
13	13	2	14	170	2198	28562
14	2×7	4	24	250	3096	40834
15	3×5	4	24	260	3528	51332
16	24	5	31	341	4681	69905
17	17	2	18	290	4914	83522
18	2×32	6	39	455	6813	112931
19	19	2	20	362	6860	130322
20	22×5	6	42	546	9198	170898
21	3×7	4	32	500	9632	196964
22	2×11	4	36	610	11988	248914
23	23	2	24	530	12168	279842
24	23×3	8	60	850	16380	358258
25	52	3	31	651	15751	391251
26	2×13	4	42	850	19782	485554
27	33	4	40	820	20440	538084
28	22×7	6	56	1050	25112	655746
29	29	2	30	842	24390	707282
30	2×3×5	8	72	1300	31752	872644
31	31	2	32	962	29792	923522
32	25	6	63	1365	37449	1118481
33	3×11	4	48	1220	37296	1200644
34	2×17	4	54	1450	44226	1419874
35	5×7	4	48	1300	43344	1503652
36	22×32	9	91	1911	55261	1813539
37	37	2	38	1370	50654	1874162
38	2×19	4	60	1810	61740	2215474
39	3×13	4	56	1700	61544	2342084
40	23×5	8	90	2210	73710	2734994
41	41	2	42	1682	68922	2825762
42	2×3×7	8	96	2500	86688	3348388
43	43	2	44	1850	79508	3418802
44	22×11	6	84	2562	97236	3997266
45	32×5	6	78	2366	95382	4158518
46	2×23	4	72	2650	109512	4757314
47	47	2	48	2210	103824	4879682
48	24×3	10	124	3410	131068	5732210
49	72	3	57	2451	117993	5767203
50	2×52	6	93	3255	141759	6651267

특성.

주요국의 공식

소수 p의 경우,

${\displaystyle {\regated}\jourma _{0}(p)&=2\\\\\n^{n}\n+1\\ndma _{1}(p)&=p+1\ended}}}}}$

왜냐하면, 정의에 따르면, 소수 인자는 1이고 그 자체이기 때문이다. 또한_n p#이 원류를 나타내는 곳에서는

${\displaystyle \sigma_{0}(p_{n}\#)=2^{n}}}$

n개의 주요 인자는 형성된 각 적절한 구분자에 대해 n개 항에서 이진 선택(${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$ 또는$$ 1)의 순서를 허용하기 때문이다.

분명히, ()> ${\displaystyle n>2$에 1 $<<\sigma _{0}(n$과$,$1 > > ${\displaystyle n>1$},0$<$$displaystyle$ $}$에 대한 1 $<<\sigma _{0$$($$n)>.$

분점 함수는 승수지만 완전히 승수는 아니다.^[why?]

${\displaystyle \gcd(a,b)=1\Longrigharrow \sigma _{x}(ab)=\sigma _{x}(b).}$

이것의 결과는, 우리가 글을 쓴다면

${\displaystyle n=\prod _{i=1}^{r}p_{i}^{a_{i}}}}$

여기서 r = Ω(n)은 n의 구별되는 주요 인자의 수, p는_i ith 주요 인자의 수_i, a는 n이 분할되는 p의_i 최대 힘이다. 그러면 우리는 다음을 가진다.

${\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}\sum _{j=0}^{a_{i}}p_{i}^{jx}=\prod _{i=1}^{r}\left(1+p_{i}^{x}+p_{i}^{2x}+\cdots +p_{i}^{a_{i}x}\right).}$

x ≠ 0인 경우, 이 값은 유용한 공식과 동일하다.

${\displaystyle \x}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{p_{i}+1){p_{x}-1}{p_{i}-1}.}$

x = 0일 때 d(n)은 다음과 같다.

${\displaystyle \prodma _{0}(n)=\prod _{i=1}^{r}(a_{i}+1)}$

This result can be directly deduced from the fact that all divisors of ${\displaystyle n}$ are uniquely determined by the distinct tuples ${\displaystyle (x_{1},x_{2},...,x_{i},...,x_{r})}$ of integers with ${\displaystyle 0\leq x_{i}\leq a_{i}}$ (i.e. ${\displaystyle i_{}}$+ ${\displaystyle 1}$ ${\displaystyle a_{i}+1$} 각 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$에 대한 독립적$$ 선택 항목$.$

예를 들어, n이 24인 경우 두 가지 주요 요인(p는₁ 2이고₂ p는 3)이 있는데, 24가 2³×3의¹ 산물이고, a가₁ 3이고, a가₂ 1이라는 점에 주목한다. ${\displaystyle {따라서\mathrm{}}_{}}$ as$$ 0${\displaystyle {}_{}}$( ${\displaystyle 24}$) ${\displaystyle \sigma _{0}(24)$을 다음과 같이 계산할 수 있다.

${\displaystyle \prod_{0}(24)=\prod_{i}^{2}(a_{i}+1)=(3+1)=4\cdot 2=8.}$

이 공식에 의해 계산된 8개의 구분자는 1, 2, 4, 8, 3, 6, 12, 24이다.

기타 속성 및 ID

오일러는 이 놀라운 재발을 증명했다.^[5][6][7]

${\displaystyle {\begin{aligned}\sigma (n)&=\sigma (n-1)+\sigma (n-2)-\sigma (n-5)-\sigma (n-7)+\sigma (n-12)+\sigma (n-15)+\cdots \\&=\sum _{i\in \mathbb {Z} }(-1)^{i+1}\left(\sigma \left(n-{\frac {1}{2}}\left(3i^{2}-i\right)\right)+\sigma \left(n-{\frac {1}{2}}\left(3i^{2}+i\right)\right)\right)\end{aligned}}}$

where ${\displaystyle \sigma (0)=n}$ if it occurs and ${\displaystyle \sigma (i)=0}$ for ${\displaystyle i\leq 0,}$ ${\displaystyle {\tfrac {1}{2}}\left(3i^{2}-i\right)}$ are the pentagonal numbers. 실제로 오일러는 자신의 펜타곤 수 정리 속에서 정체성의 로그 분화를 통해 이를 증명했다.

For a non-square integer, n, every divisor, d, of n is paired with divisor n/d of n and ${\displaystyle \sigma _{0}(n)}$ is even; for a square integer, one divisor (namely ${\displaystyle {\sqrt {n}}}$) is not paired with a distinct divisor and ${\displaystyle \sigma _{0}(n)}$ is odd. 마찬가지로 숫자 ${\displaystyle \sigma }$ ${\displaystyle {1\mathrm{}}_{}}$( n${\displaystyle }$) ${\displaystyle \sigma _{1}(n)}$은 n이 정사각형인 경우 또는 두 번 정사각형인 경우에만 홀수다$$.^{[citation needed]}

또한 s(n) = σ(n) - n. 여기서 s(n)는 n의 적절한 구분자, 즉 n 자체를 제외한 n의 구분자의 합을 나타낸다. 이 함수는 s(n) = n인 n의 완전한 숫자를 인식하는 데 사용되는 것이다. 만약 s(n) > n이면 n은 풍부한 숫자, s(n) < n이면 n은 부족한 숫자다.

예를 $들어{\displaystyle }$ n = 2${\displaystyle k^{}}$ ${\$power${\displaystyle (n}$ )${\displaystyle }$= 2 ${\displaystyle \cdot }$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle \mathrm{k}{}^{}}$- 1${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle n^{}}$- ${\displaystyle 1}$,${\displaystyle \sigma(n)=2\cdot 2^{k}-1=$2n-1}, s(n) = n - 1의 검정력이면 n은 거의 완벽하다.

예를 들어, p < q를 가진 두 개의 뚜렷한 primes p와 q의 경우,

${\displaystyle n=pq.}$

그러면

${\displaystyle \sigma(n)=(p+1)=n+1+(p+q),}$

${\displaystyle \varphi(n)=(p-1)=n+1-(p+q),}$

, 그리고

${\displaystyle n+1=(\displayma(n)+\varphi(n)/2,}$

${\displaystyle p+q=(\displayma(n)-\varphi(n)/2,}$

여기서 $\phi {\displaystyle }$(${\displaystyle n}$) ${\displaystyle \varphi (n)}$은(는) 오일러의 토털 함수다.

그 다음, 그 뿌리는 다음과 같다.

${\displaystyle (x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\ma (n)-\varphi (n)/2]x+[\ma (n)+\varphi (n)/2-1]=0}$

p와 q를 σ(n)과 φ(n)로만 표현하도록 허용하며, n이나 p+q를 알지도 못하면서 다음과 같이 표현한다.

${\displaystyle p=(n)-\varphi(n)/4-{\sqrt{[\bma(n)-\varphi(n)/4]^{2}-[(n)+\varphi(n)/2-1]},},}$

${\displaystyle q=(n)-\varphi(n)/4+{\sqrt{[\bma(n)-\varphi(n)/4]^{2}-[(n)+\varphi(n)/2-1]}}}.}$

또한 n과 $\sigma {\displaystyle }$(${\displaystyle n}$) ${\$displaystyle$\sigma ($n)} 또는$$ $\phi {\displaystyle }$(${\displaystyle n}$${\displaystyle )}$ ${\displaystyle$ $\$$varphi (n)}($또는 p+q와 $\sigma {\displaystyle )}$ ${\displaystystyle$$\sigma$ ($n$ 또는$$ $\phi {\displaystyle }$($)$를$$알면 p와 $q$를 쉽게 찾을 수 있다.

1984년, 로저 히스 브라운은 평등함을 증명했다.

${\displaystyle \sigma _{0}(n)=\sigma _{0}(n+1)}$

n의 무한대에 대해 참이다(OEIS: A005237 참조).

시리즈 관계

디비저 함수와 관련된 두 개의 디리클레 시리즈는 다음과 같다.

${\displaystyle \sum \{n=1}^{\inflit }{\frac {\n(n)}{n^{s}}}=\제타(s)\jeta(s-a)\competition{\text for}}}\competition s>1,s>a+1,},},},}$

d(n) = σ₀(n)에 대해 다음을 제공한다.

${\displaystyle \sum _{n=1}^{\inflt }{d(n)}{n^{s}}}=\제타 ^{2}(s)\reason{\text{for}}}}}\data ^1,}$

라마누잔의 정체성^[9]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}},}$

란킨-셀버그 콘볼루션의 특별한 경우야

Divisor 함수와 관련된 Lambert 시리즈는 다음과 같다.

${\displaystyle \sum _{n=1}^{\infty }q^{n}\sigma _{a}(n)=\sum _{n=1}^{\infty }\sum _{j=1}^{\infty }n^{a}q^{j\,n}=\sum _{n=1}^{\infty }{\frac {n^{a}q^{n}}{1-q^{n}}}}$

임의 복합 q q 1 및 a의 경우. 이 합계는 아이젠슈타인 시리즈의 푸리에 시리즈와 바이에스트라스 타원함수의 불변수로도 나타난다.

> ${\displaystyle k>0$의 경우 다음과 같이$$ Ramanujan sums $c{\displaystyle {}_{}n}$ ${\displaystyle )}$ m (n ) ${\displaystyle c_{m}(n)}$을(를) 사용하여 명시적인 시리즈 표현이 있다.^[11]

${\displaystyle \k}(n)=\zeta (k+1)n^{k}\sum _{m=1}^{m=1}{n}{m^{k+1}}}.}$

$c{\displaystyle {}_{}}$ ${\displaystyle m{}_{}}$( n$){\displaystyle c_{m}(n)}$의 첫 번째 항을 계산하면$$ "평균값" $\zeta {\displaystyle }$ ${\displaystyle (\mathrm{k}}$+ 1${\displaystyle }$) ${\displaystyle {}^{}}$ ${\displaystyle k^{}}$ ${\$ :

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\left[1+{\frac {(-1)^{n}}{2^{k+1}}}+{\frac {2\cos {\frac {2\pi n}{3}}}{3^{k+1}}}+{\frac {2\cos {\frac {\pi n}{2}}}{4^{k+1}}}+\cdots \right]}$

성장률

리틀오 표기법에서 이분함수는 불평등을 만족시킨다.^[12][13]

${\displaystyle {\mbox{모두 }}}\barespsilon >0,\barepsilon(n)=o(n^{\barespsilon })).}$

좀 더 정확히 말하면, Severin ^[13]Wigert는 다음과 같은 것을 보여주었다.

${\displaystyle \imsup _{n\to \inflt }{\frac {\log d(n)}{\log n/\log n}=\log 2.}$

반면에, 무한히 많은 소수들이 있기 때문에,^[13]

${\displaystyle \liminf _{n\to \infty }d(n)=2.}$

Big-O 표기법에서 피터 구스타프 르주네 디리클레트는 분음함수의 평균 순서가 다음과 같은 불평등을 만족시킨다는 것을 보여주었다.^[14][15]

${\displaystyle {\mbox{{{}x\geq 1,\sum _{n\leq x}d(n)=x\log x+(2\gamma -1)x+O({\sqrt {x}),}$

여기서 $\gamma {\displaystyle }$ ${\displaystyle \gamma}$은(는) 오일러의 감마 상수다. 이 공식에서$$ 바인딩된 $O{\displaystyle }$( ${\displaystyle x}$)$${\$displaystyle O({\sqrt{x}}})$를 개선하는 것을 Dirichlet의 divisor 문제로 알려져 있다.

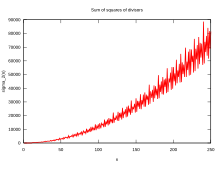
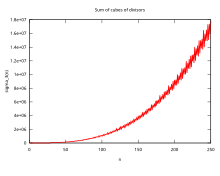
시그마 함수의 동작은 불규칙하다. 시그마 함수의 점증적 성장률은 다음과 같이 표현할 수 있다.

${\displaystyle \limsup _{n\rightarrow \inflit }{\frac {\prow (n)}{n\,\log n}=e^{\log }}}$

여기서 림섭이 한도가 상위에 있다. 이 결과는 1913년(그룬월 1913년)에 발표된 그룬월(Grönwall 1913년)의 정리다. 그의 증거는 머텐스의 세 번째 정리를 사용하는데, 이 정리는 다음과 같다.

${\displaystyle \lim_{n\to \inflat }{\frac {1}{\log n}\prod_{p\leq n}{p-1}{p-1}=e^{\message }}}}}$

여기서 p는 전성기를 의미한다.

1915년, 라마누잔은 리만 가설을 전제로 하여 불평등이 다음과 같이 증명되었다.

( )< n ${\displaystyle \sigma (n)<e^{\gamma }n\log \log n}$ (로빈 부등식)

충분히 큰 n을 보유한다(Ramanujan 1997). 불평등을 위반하는 가장 큰 알려진 가치는 n=5040이다. 1984년 가이 로빈은 리만 가설이 사실일 경우에만 불평등이 n > 5040 모두에 대해 사실임을 증명했다(로빈 1984). 이것이 로빈의 정리인데, 그의 뒤를 이어 불평등이 알려지게 되었다. 로빈은 더 나아가 리만 가설이 거짓이라면 불평등을 위반하는 n의 값이 무한히 많다는 것을 보여주었고, 그러한 n > 5040의 가장 작은 값이 반드시 초복적이어야 한다고 알려져 있다(Akbary & Frigstad 2009). 불평등은 큰 홀수 및 제곱이 없는 정수를 유지하며, 리만 가설은 소수 5번째 힘에 의해 분리될 수 없는 것에 대한 불평등과 동등하다는 것이 밝혀졌다(Choie et al. 2007).

로빈은 또한 불평등이 다음과 같이 무조건적으로 증명했다.

${\displaystyle \e^{\reason }n\log \log n+{0.6483\n}{\log \n}}}$

모든 엔 3 3의 홀드.

이와 관련된 경계는 2002년 제프리 라고리아스에 의해 주어졌는데, 그는 리만 가설이 다음과 같은 진술과 동일하다는 것을 증명했다.

$\displaystyle \sigma(n)<H_{n}+\log(H_{n})e^{H_{n}}}$

모든 자연수 n > 1에 대해, $여기$서 H ${\displaystyle n_{}}$ ${\$는 n번째 조화수(Lagarias 2002)이다.

참고 항목

• 디비저 합계 경련, 디비저 함수와 관련된 몇 가지 정체성
• 오일러의 토털함수 오일러의 피함수
• 리팩터블 넘버
• 칸막이 표
• 유니터리 디비저

메모들

참고문헌

• Akbary, Amir; Friggstad, Zachary (2009), "Superabundant numbers and the Riemann hypothesis" (PDF), American Mathematical Monthly, 116 (3): 273–275, doi:10.4169/193009709X470128, archived from the original (PDF) on 2014-04-11.
• Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
• 바흐, 에릭; 핼릿, 제프리, 알고리즘 번호 이론, 제1권, 1996년 MIT 프레스. ISBN 0-262-02405-5, 섹션 8.8의 234페이지를 참조하십시오.
• Caveney, Geoffrey; Nicolas, Jean-Louis; Sondow, Jonathan (2011), "Robin's theorem, primes, and a new elementary reformulation of the Riemann Hypothesis" (PDF), INTEGERS: The Electronic Journal of Combinatorial Number Theory, 11: A33, arXiv:1110.5078, Bibcode:2011arXiv1110.5078C
• Choie, YoungJu; Lichiardopol, Nicolas; Moree, Pieter; Solé, Patrick (2007), "On Robin's criterion for the Riemann hypothesis", Journal de théorie des nombres de Bordeaux, 19 (2): 357–372, arXiv:math.NT/0604314, doi:10.5802/jtnb.591, ISSN 1246-7405, MR 2394891, S2CID 3207238, Zbl 1163.11059
• Grönwall, Thomas Hakon (1913), "Some asymptotic expressions in the theory of numbers", Transactions of the American Mathematical Society, 14: 113–122, doi:10.1090/S0002-9947-1913-1500940-6
• Hardy, G. H.; Wright, E. M. (2008) [1938], An Introduction to the Theory of Numbers, Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.), Oxford: Oxford University Press, ISBN 978-0-19-921986-5, MR 2445243, Zbl 1159.11001
• Ivić, Aleksandar (1985), The Riemann zeta-function. The theory of the Riemann zeta-function with applications, A Wiley-Interscience Publication, New York etc.: John Wiley & Sons, pp. 385–440, ISBN 0-471-80634-X, Zbl 0556.10026
• Lagarias, Jeffrey C. (2002), "An elementary problem equivalent to the Riemann hypothesis", The American Mathematical Monthly, 109 (6): 534–543, arXiv:math/0008177, doi:10.2307/2695443, ISSN 0002-9890, JSTOR 2695443, MR 1908008, S2CID 15884740
• Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
• Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77081766
• Ramanujan, Srinivasa (1997), "Highly composite numbers, annotated by Jean-Louis Nicolas and Guy Robin", The Ramanujan Journal, 1 (2): 119–153, doi:10.1023/A:1009764017495, ISSN 1382-4090, MR 1606180, S2CID 115619659
• Robin, Guy (1984), "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann", Journal de Mathématiques Pures et Appliquées, Neuvième Série, 63 (2): 187–213, ISSN 0021-7824, MR 0774171
• Williams, Kenneth S. (2011), Number theory in the spirit of Liouville, London Mathematical Society Student Texts, vol. 76, Cambridge: Cambridge University Press, ISBN 978-0-521-17562-3, Zbl 1227.11002

• Weisstein, Eric W. "Divisor Function". MathWorld.
• Weisstein, Eric W. "Robin's Theorem". MathWorld.
• Huard, Ou, Spearman 및 Williams가 작성한 논문의 PDF 기능을 포함하는 특정 콘볼루션 합계의 기초 평가. 기본적(즉, 모듈형 형태 이론에 의존하지 않음) 분할 합계의 증명, 숫자를 삼각형 숫자의 합으로 나타내는 방법의 수에 대한 공식 및 관련 결과를 포함한다.