뫼스바우어 분광법

Mössbauer spectroscopy
Fe의 뫼스바우어 흡수 스펙트럼

뫼스바우어 분광법은 뫼스바우어 효과를 기반으로 한 분광 기법입니다. 루돌프 뫼스바우어가 1958년에 발견한 이 효과는 고체에서 핵 감마선의 거의 반동이 없는 방출과 흡수로 이루어져 있습니다. 그에 따른 핵분광법은 특정 핵의 화학적 환경의 작은 변화에 절묘하게 민감합니다.

일반적으로 세 가지 유형의 핵 상호작용이 관찰될 수 있습니다. 가까운 전자 밀도의 차이로 인한 이성질체 이동(구 문헌의 화학적 이동이라고도 함), 원자 규모 전기장 구배로 인한 4중극 분열, 핵이 아닌 자기장으로 인한 자기 제만 분열. 핵 감마선의 높은 에너지와 극도로 좁은 선폭으로 인해 뫼스바우어 분광법은 에너지11(따라서 주파수) 분해능 측면에서 매우 민감한 기술로 10분의 몇 부분의 변화만 감지할 수 있습니다. 핵자기공명분광법과는 전혀 무관한 방법입니다.

기본원리

주 기사: 뫼스바우어 효과

총알이 발사되었을 때 총이 반동하는 것과 마찬가지로, 운동량 보존을 위해서는 감마선 방출 또는 흡수 중에 반동하는 핵이 필요합니다. 정지한 핵이 감마선을 방출하면 감마선의 에너지는 전이의 자연 에너지보다 약간 적지만 정지한 핵이 감마선을 흡수하려면 감마선의 에너지가 자연 에너지보다 약간 커야 하는데, 두 경우 모두 에너지가 반동하기 위해 손실되기 때문입니다. 이것은 에너지의 이동이 너무 크고 방출 스펙트럼과 흡수 스펙트럼이 크게 겹치지 않기 때문에 자유 핵에서는 핵 공명(동일한 핵에 의한 동일한 감마선의 방출 및 흡수)이 관찰되지 않는다는 것을 의미합니다.

그러나 고체 결정 내의 핵은 결정 격자 내에서 제자리에 묶여 있기 때문에 자유롭게 반동할 수 없습니다. 고체의 핵이 감마선을 방출하거나 흡수할 때, 여전히 일부 에너지는 반동 에너지로 손실될 수 있지만, 이 경우 항상 포논(결정 격자의 양자화된 진동)이라고 불리는 이산 패킷에서 발생합니다. "반동 없는" 이벤트로 알려진 0을 포함하여 모든 수의 포논이 방출될 수 있습니다. 이 경우 운동량 보존은 결정 전체의 운동량에 의해 충족되므로 실질적으로 에너지가 손실되지 않습니다.[1]

Mössbauer는 방출 및 흡수 이벤트의 상당 부분이 반동이 없을 것이라는 것을 발견했으며, 이는 Lamb-Mössbauer 인수를 사용하여 정량화됩니다.[2] 이 사실이 뫼스바우어 분광법을 가능하게 하는 것인데, 하나의 핵에서 방출되는 감마선이 같은 동위원소의 핵을 포함하는 시료에 의해 공명 흡수되고, 이 흡수량을 측정할 수 있다는 것을 의미하기 때문입니다.

뫼스바우어 흡수의 반동 분율은 핵 공명 진동 분광법으로 분석됩니다.

전형적인 방법

가장 일반적인 형태인 뫼스바우어 흡수 분광법은 고체 샘플을 감마선 빔에 노출시키고 검출기는 샘플을 통해 전송되는 빔의 세기를 측정합니다. 감마선을 방출하는 소스의 원자는 샘플의 원자와 동일한 동위원소여야 합니다.

만약 방출하는 핵과 흡수하는 핵이 동일한 화학적 환경에 있다면 핵 전이 에너지는 정확히 같으며 두 물질 모두 정지한 상태에서 공명 흡수가 관찰될 것입니다. 그러나 화학적 환경의 차이로 인해 아래에 설명된 것처럼 원자력 에너지 수준이 몇 가지 다른 방식으로 변화합니다. 이러한 에너지 이동은 매우 작지만(일반적으로 마이크로 전자볼트보다 작음), 일부 방사성 핵종에 대한 감마선의 매우 좁은 스펙트럼 선폭은 작은 에너지 이동을 흡광도의 큰 변화에 대응시킵니다. 두 핵을 공진으로 되돌리기 위해서는 감마선의 에너지를 약간 변경해야 하며 실제로는 항상 도플러 쉬프트를 사용하여 수행됩니다.

뫼스바우어 흡수 분광법 동안 소스는 선형 모터를 사용하여 일정 범위의 속도를 통해 가속되어 도플러 효과를 생성하고 주어진 범위를 통해 감마선 에너지를 스캔합니다. 예를 들어 Fe에 대한 일반적인 속도 범위는 ±11mm/s(1mm/s = 48.075neV)일 수 있습니다.

결과 스펙트럼에서 감마선 강도는 소스 속도의 함수로 표시됩니다. 샘플의 공진 에너지 수준에 해당하는 속도에서 감마선의 일부가 흡수되어 측정된 강도가 떨어지고 그에 따라 스펙트럼이 감소합니다. 딥의 수, 위치 및 강도(피크라고도 함, 전송 강도의 딥은 흡광도의 피크)는 흡수 핵의 화학적 환경에 대한 정보를 제공하고 샘플을 특성화하는 데 사용할 수 있습니다.

적합한 소스 선택

적합한 감마선 소스는 원하는 동위원소로 붕괴하는 방사성 모체로 구성됩니다. 예를 들어, Fe의 근원은 전자 포획에 의해 Fe의 들뜬 상태로 붕괴되는 Co로 구성되어 있으며, 뫼스바우어 효과를 나타내는 일련의 감마선 방출을 통해 바닥 상태로 붕괴됩니다. 방사성 코발트는 종종 로듐의 호일에 준비됩니다.[4] 이상적으로 모 동위원소는 편리한 반감기를 가질 것입니다. 또한 감마선 에너지가 상대적으로 낮아야 합니다. 그렇지 않으면 시스템의 반동 없는 분율이 낮아 신호 대 잡음비가 떨어지고 긴 수집 시간이 필요합니다. 아래의 주기율표는 뫼스바우어 분광법에 적합한 동위원소를 가진 원소들을 나타냅니다. 이 중 Fe는 I, Sn 및 Sb도 빈번하게 연구되고 있지만, 이 기술을 사용하여 연구된 가장 일반적인 원소입니다.

뫼스바우어 활성 원소의 주기율표
H 그
리 있다 B C N O F 네
나 Mg 알 시 P S 클 아르
K 카 스크 티 V Cr Mn 페 코 니 CU Zn 가 게 ~하듯이 세 브르 크르
Rb 스르 Y Zr Nb 모 Tc 루 Rh PD 아그 Cd 인 Sn Sb 테 I Xe
Cs 바 라 Hf 타 W 레 오스 어 Pt 아우 흐그 Tl 피비 비 포 앳 Rn
프르 라 아크 알프 db Sg Bh ㅎ 산 Ds Rg 씨엔 응 플 맥 Lv 츠 오그
쎄 프르 Nd 피엠 스엠 에우 그디 Tb 다이 호 음.정말 Tm 이브 루
그 파 U Np 푸 암 씨엠 Bk cf 에스 에프엠 Md 아니요. Lr
뫼스바우어 활성 원소 감마선 소스 뫼스바우어에게 적합하지 않음

뫼스바우어 스펙트럼 분석

위에서 설명한 바와 같이 뫼스바우어 분광법은 매우 미세한 에너지 분해능을 가지고 있으며 관련 원자의 핵 환경의 미세한 변화까지도 감지할 수 있습니다. 일반적으로 관찰되는 핵 상호작용은 이성질체 이동, 4극 분열, 초미세 자기 분열의 세 가지 유형입니다.[5][6]

이성질체 이동

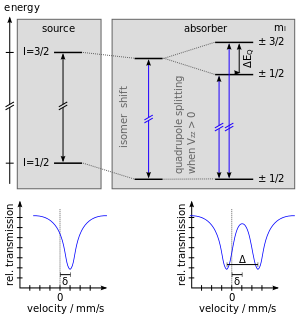
그림 2: 핵에너지 준위와 그에 상응하는 뫼스바우어 스펙트럼의 화학적 이동과 4극 분할

이성질체 이동(δ)(특히 오래된 문헌에서는 화학 이동이라고도 함)은 궤도 내 전자의 전이로 인한 핵의 공명 에너지 이동(그림 2 참조)을 설명하는 상대적인 척도입니다. 전체 스펙트럼은 핵의 전자 전하 밀도에 따라 양 또는 음의 방향으로 이동합니다. 이러한 변화는 0이 아닌 확률 궤도 전자와 궤도를 도는 0이 아닌 부피 핵 사이의 정전기 반응의 변화로 인해 발생합니다.

궤도상의 전자만이 핵에서 발견될 확률이 0이 아닙니다(원자 궤도 참조). 그러나 p, d, f 전자는 스크리닝 효과를 통해 전자 밀도에 영향을 미칠 수 있습니다.

이성질체 이동은 아래의 식을 이용하여 나타낼 수 있는데, 여기서 K는 핵상수이고, R과 R의 차이는 들뜬 상태와 바닥 상태의 유효 핵전하 반경 차이이며, [[ ψ(0)]]과 [[ ψ(0)]]의 차이는 핵 내의 전자 밀도 차이(a = source, b = sample). 여기에 설명된 화학 이성질체 이동은 온도에 따라 변하지 않지만 뫼스바우어 스펙트럼은 2차 도플러 효과로 알려진 상대론적 효과로 인해 온도 민감성을 가집니다. 일반적으로 이 효과의 영향은 작으며 IUPAC 표준은 Isomer Shift를 수정하지 않고 보고할 수 있습니다.[7]

이 방정식의 물리적 의미는 다음과 같은 예를 사용하여 명확히 할 수 있습니다.

  1. Fe 스펙트럼에서 s-전자 밀도의 증가는 유효 핵 전하의 변화가 음이기 때문에 음의 이동을 제공하는 반면(R < R로g 인해), Sn에서 s-전자 밀도의 증가는 전체 핵 전하의 양의 변화로 인해 양의ee 이동을g 제공합니다(R > R로 인해).
  2. 산화된 제2철 이온(Fe3+)은 제1철 이온(Fe2+)보다 이성질체 이동이 더 낮은 이유는 제2철 이온의 핵에서 s-전자 밀도가 d 전자에 의한 더 약한 스크리닝 효과로 인해 더 크기 때문입니다.[8]

이성질체 이동은 산화 상태, 원자가 상태, 전자 차폐 및 전기 음성 그룹의 전자 인출력을 결정하는 데 유용합니다.[5]

사중극 쪼개기

그림 3: 니트로프루시드 나트륨은 4중극 분할을 나타내는 일반적인 참조 물질입니다.

4중극 분할은 핵에너지 수준과 주변 전기장 구배(EFG) 사이의 상호작용을 반영합니다. 비구형 전하 분포를 가진 상태의 핵, 즉 스핀 양자수(I)가 1/2보다 큰 모든 핵은 핵 사중극 모멘트를 가질 수 있습니다. 이 경우 비대칭 전기장(비대칭 전자 전하 분포 또는 리간드 배열에 의해 생성됨)이 핵 에너지 수준을 분할합니다.[5]

Fe 또는 Sn과 같이 I = 3/2의 여기상태를 갖는 동위원소의 경우 여기상태는 m = ±1/2 및 m = ±3/2의 두 가지 기질로 나누어집니다. 여기 상태 전이에 대한 접지는 스펙트럼에서 두 개의 특정 피크로 나타나며 때로는 "더블트"라고 합니다. 4중극 분할은 이 두 피크 사이의 분리로 측정되며 핵에서 전기장의 특성을 반영합니다.

4중극 분할은 산화 상태, 스핀 상태, 부위 대칭 및 리간드 배열을 결정하는 데 사용할 수 있습니다.[5]

그림 4: Mossbauer 스펙트럼과 Fe에서 자기적인 Zeeman 분할을 나타낸 그림.

자기 초미세 분열

자기 초미세 분열은 제만 효과에 의해 설명된 바와 같이 핵과 주변 자기장 사이의 상호작용의 결과입니다. 스핀 I을 가진 핵은 자기장이 존재하면 2I + 1개의 하위 에너지 준위로 분열합니다. 예를 들어 스핀 상태 I = 3/2인 Fe 핵의 첫 번째 여기 상태는 m 값이 +3/2, +1/2, -1/2 및 -3/2인 4개의 비퇴화 하위 상태로 분할됩니다. 등간격 분할은 10eV−7 정도로 초미세하다고 합니다. 자기 쌍극자 전이에 대한 선택 규칙은 여기 상태와 접지 상태 사이의 전이는 m이I 0 또는 1 또는 -1만큼 변화하는 경우에만 발생할 수 있음을 의미합니다. 이렇게 하면 3/2에서 1/2 전환에 대해 6개가 가능합니다.[5]

분열의 정도는 핵에서의 자기장 세기에 비례하며, 결국 핵의 전자 분포("화학적 환경")에 따라 달라집니다. 예를 들어, 시료 호일을 진동원과 광자 검출기 사이에 배치하여(그림 5 참조), 그림 4와 같이 흡수 스펙트럼을 생성하여 분할을 측정할 수 있습니다. 핵 상태의 양자 "g인자"가 알려져 있다면, 자기장은 피크 사이의 간격으로부터 결정될 수 있습니다. 많은 철 화합물을 포함한 강자성 물질에서는 자연 내부 자기장이 상당히 강하고 그 영향이 스펙트럼을 지배합니다.

모든 것의 조합

이성질체 이동, 4중극 분할 및 초미세 분할의 세 가지 Mössbauer 매개변수는 표준에 대한 스펙트럼과 비교하여 특정 화합물을 식별하는 데 종종 사용될 수 있습니다.[9] 경우에 따라, 화합물은 뫼스바우어 활성 원자에 대해 하나 이상의 가능한 위치를 가질 수 있습니다. 예를 들어, 자철석(FeO34)의 결정 구조는 철 원자에 대한 두 개의 서로 다른 부위를 지지합니다. 스펙트럼에는 뫼스바우어 매개변수의 두 세트에 해당하는 각 잠재적 원자 부위에 대한 6개의 집합인 12개의 피크가 있습니다.

이성질체 이동, 4중극 분할, 자기 제만 효과 등의 모든 효과가 여러 번 관찰됩니다. 이러한 경우 이성질체 이동은 모든 선들의 평균에 의해 주어집니다. 4개의 여기된 기질이 모두 동일하게 이동할 때(2개의 기질이 들어 올려지고 나머지 2개는 내려짐) 4중극 분할은 내부 4개의 선에 대한 외부 2개의 선의 이동(모든 내부 4개의 선이 가장 바깥쪽 2개의 선에 반대로 이동함)에 의해 주어집니다. 일반적으로 정확한 값을 위해 적합한 소프트웨어가 사용됩니다.

또한 다양한 피크의 상대적 강도는 샘플 내 화합물의 상대적 농도를 반영하며 반정량적 분석에 사용할 수 있습니다. 또한 강자성 현상은 크기에 의존하기 때문에 경우에 따라 스펙트럼은 물질의 결정체 크기와 결정립 구조에 대한 통찰력을 제공할 수 있습니다.

뫼스바우어 방출 분광법

뫼스바우어 방출 분광법은 방출 요소가 탐침 샘플에 있고 흡수 요소가 기준에 있는 뫼스바우어 분광법의 전문적인 변형입니다. 가장 일반적으로 이 57기법은 Co/Fe 쌍에 적용됩니다. 대표적인 응용 분야는 수소 탈황에 사용되는 비정질 Co-Mo 촉매에서 코발트 사이트의 특성화입니다. 그런 경우 샘플에 Co가 도핑됩니다.[10]

적용들

이 기술의 단점 중에는 제한된 수의 감마선 소스와 핵의 반동을 제거하기 위해 샘플이 고체여야 한다는 요구 사항이 있습니다. 뫼스바우어 분광법은 산화 상태 변화, 특정 원자에 대한 서로 다른 리간드의 영향, 시료의 자기 환경 등 핵의 화학적 환경의 미묘한 변화에 대한 민감성이 독특합니다.

뫼스바우어 분광법은 지질학 분야에서 특히 운석과 달 암석을 포함한 철 함유 표본의 구성을 확인하는 데 유용했습니다. 뫼스바우어 스펙트럼의 현장 데이터 수집은 화성의 철이 풍부한 암석에서도 수행되었습니다.[11][12]

또 다른 응용 분야에서는 Fischer-Tropsch 합성에 사용되는 철 촉매의 상변화를 특성화하기 위해 Mössbauer 분광법을 사용합니다. 처음에는 헤마타이트(FeO23)로 구성되어 있지만 이러한 촉매는 마그네타이트(FeO34)와 여러 철 탄화물의 혼합물로 변환됩니다. 탄화물의 형성은 촉매 활성을 향상시키는 것으로 보이지만 촉매 입자의 기계적 분해 및 마모를 유발할 수 있으며, 이는 반응 생성물로부터 촉매의 최종 분리에 어려움을 초래할 수 있습니다.[13]

뫼스바우어 분광법은 올레핀의 선택적 산화 동안 안티몬(Sb)의 산화 상태의 상대적 농도 변화를 결정하는 데에도 사용되었습니다. 하소 과정에서 안티몬 함유 이산화주석 촉매의 모든 Sb 이온은 +5 산화 상태로 변합니다. 촉매 반응 후 거의 모든 Sb 이온은 +5에서 +3 산화 상태로 되돌아갑니다. 안티몬 핵을 둘러싼 화학적 환경의 상당한 변화는 산화 상태 변화 동안 발생하며, 이는 뫼스바우어 스펙트럼의 이성질체 이동으로 쉽게 모니터링할 수 있습니다.[14]

이 기술은 또한 매우 높은 에너지 분해능 때문에 상대성 이론에 의해 예측된 2차 횡단 도플러 효과를 관찰하는 데 사용되었습니다.[15]

생체무기화학

모스바우어 분광법은 생체 무기 화학, 특히 철 함유 단백질 및 효소 연구에 널리 적용되었습니다. 종종 이 기술은 철의 산화 상태를 결정하는 데 사용됩니다. 철을 포함한 생체 분자의 대표적인 예로는 철-황 단백질, 페리틴 및 사이토크롬을 포함한 헴이 있습니다. 이러한 연구는 종종 관련 모델 단지에 대한 분석으로 보완됩니다.[16][17] 특히 관심 있는 분야는 철 단백질에 의한 산소 활성화에 관여하는 중간체의 특성화입니다.[18]

Fe가 풍부한 생체 분자의 진동 스펙트럼은 핵 공명 진동 분광법(NRVS)을 사용하여 얻을 수 있으며, 여기서 샘플은 뫼스바우어 흡광도 주파수를 중심으로 하는 싱크로트론 생성 X선 범위를 통해 스캔됩니다. 스펙트럼의 스톡스 및 반 스톡스 피크는 저주파 진동에 해당하며 대부분은 600 cm−1 미만이고 일부는 100 cm−1 미만입니다.

뫼스바우어 분광계

그림 5: 투과식 뫼스바우어 분광기의 개략도

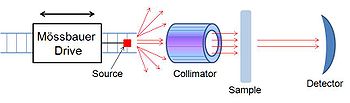
뫼스바우어 분광기는 뫼스바우어 분광법을 수행하는 장치 또는 뫼스바우어 효과를 이용하여 시료에 존재하는 뫼스바우어 핵의 화학적 환경을 결정하는 장치입니다. 도플러 효과를 발생시키기 위해 앞뒤로 움직이는 소스, 평행하지 않은 감마선을 걸러내는 콜리메이터 및 검출기의 세 가지 주요 부분으로 구성됩니다.

미모스 II(MB)라는 이름의 미니어처 뫼스바우어 분광계는 NASA의 화성 탐사 로버 임무에서 두 탐사선에 의해 사용되었습니다.[19]

57페 뫼스바우어 분광법

화학적 이성질체 이동 및 4중극 분할은 일반적으로 기준 물질에 대해 평가됩니다. 예를 들어, 철 화합물에서 뫼스바우어 파라미터는 철박(40 마이크로미터 미만의 두께)을 사용하여 평가되었습니다. 금속 철박에서 나온 6선 스펙트럼의 중심은 -0.1mm/s입니다(Co/Rh 소스의 경우). 다른 철 화합물의 모든 이동은 이 -0.10 mm/s(실온에서)에 대해 계산됩니다. 즉, 이 경우 이성질체 이동은 Co/Rh 공급원에 대해 상대적입니다. 즉, 뫼스바우어 스펙트럼의 중심점은 0입니다. 시프트 값은 0.0mm/s에 대해 보고될 수도 있습니다. 여기서 시프트는 철박에 대해 상대적입니다.

6선 철 스펙트럼에서 바깥쪽 선 거리를 계산하려면:

여기서 c는 빛의 속도, B는 금속 철의 내부 자기장(33T), μ는 핵마그네톤(3.1524512605×10 eV/T), E는 여기 에너지(14.412497(3) keV), g는 접지 상태 핵분열 인자(0.090604/(I), IospinI = 1 ⁄2)와 g는 Fe(-0.15532/(I, 여기서 I = 3 ⁄2)의 여기 상태 분할 계수입니다.

위의 값을 대입하면 V = 10.6258 mm/s를 얻을 수 있습니다.

철박의 다양한 품질을 반영하기 위해 다른 값이 사용되기도 합니다. 모든 경우에 V의 변화는 이성질체 이동에만 영향을 미치고 4중극 분할에는 영향을 미치지 않습니다. 뫼스바우어 분광학의 권위자인 IBAME는 특정 값을 지정하지 않기 때문에 10.60mm/s에서 10.67mm/s 사이의 값을 사용할 수 있습니다. 이러한 이유로 소스의 세부 정보(접힌 스펙트럼의 무게 중심)를 언급하면서 철박이 아닌 사용된 소스에 대한 이성질체 이동 값을 제공하는 것이 좋습니다.

참고 항목

참고문헌

  1. ^ 뫼스바우어 효과(IBME) 및 뫼스바우어 효과 데이터 센터(MEDC)의 응용에 관한 국제 위원회(International Board on Applications on the Applications of Mössbauer Effect), 뫼스바우어 효과 웹사이트 2010년 6월 3일 접속.
  2. ^ a b Gütlich, J. M.; 뫼스바우어 효과의 원리와 뫼스바우어 분광법의 기본 개념 2011-11-29를 웨이백 기계에 보관함.
  3. ^ 뫼스바우어 분광학 그룹, 왕립화학회(RSC) 웹사이트, 뫼스바우어 분광학 소개 1부 2010년 6월 3일 접속
  4. ^ Longworth, G; Window, B (1 June 1971). "The preparation of narrow-line Mössbauer sources of 57Co in metallic matrices". Journal of Physics D. 4 (6): 835–839. Bibcode:1971JPhD....4..835L. doi:10.1088/0022-3727/4/6/316. ISSN 0022-3727. S2CID 122392089. Wikidata Q56601097.
  5. ^ a b c d e 뫼스바우어 분광학 그룹, 왕립 화학 협회(RSC) 웹사이트, 뫼스바우어 분광학 소개 2부 2010년 6월 3일 접속.
  6. ^ P. Gütlich, J. M. Grenech, F. J. Berry; Mössbauer Spectroscopy: A Powerful Tool in Scientific Research Archive 2011-11-29, 2010년 6월 3일 Wayback Machine Access.
  7. ^ 뫼스바우어 효과(IBME) 및 뫼스바우어 효과 데이터 센터(MEDC)의 응용에 관한 국제 위원회, 뫼스바우어 효과 웹사이트 2017년 12월 20일 접속
  8. ^ Walker, L.; Wertheim, G.; Jaccarino, V. (1961). "Interpretation of the Fe57 Isomer Shift". Physical Review Letters. 6 (3): 98. Bibcode:1961PhRvL...6...98W. doi:10.1103/PhysRevLett.6.98.
  9. ^ 뫼스바우어 효과 데이터 센터.
  10. ^ Nagy, D. L. (1994). "Trends in Mössbauer emission spectroscopy of 57Co/57Fe". Hyperfine Interactions. 83 (1): 1–19. Bibcode:1994HyInt..83....1N. doi:10.1007/BF02074255. S2CID 95685404.
  11. ^ Klingelhöfer, G. (November 2004). "Mössbauer In Situ Studies of the Surface of Mars". Hyperfine Interactions. 158 (1–4): 117–124. Bibcode:2004HyInt.158..117K. doi:10.1007/S10751-005-9019-1. ISSN 0304-3843. S2CID 97528576. Wikidata Q29042404.
  12. ^ Schröder, Christian (2015). "Mössbauer spectroscopy in astrobiology". Spectroscopy Europe. 27 (2): 10. Retrieved 2018-01-08.
  13. ^ Sarkar, A.; et al. (2007). "Fischer–Tropsch Synthesis: Characterization Rb Promoted Iron Catalyst". Catalysis Letters. 121 (1–2): 1–11. doi:10.1007/s10562-007-9288-1. S2CID 94596943.
  14. ^ Burger, K.; Nemes-Vetéssy, Zs.; Vértes, A.; Afanasov, M. I. (April 1986). "Mössbauer spectroscopic study of the oxidation state of antimony in antimony sulfides of different composition". Journal of Chemical Crystallography. 16 (2): 295–299. doi:10.1007/BF01161115. ISSN 1074-1542. S2CID 95821984. Wikidata Q30054185.
  15. ^ Chen, Y.-L.; Yang, D.-P. (2007). "Recoilless Fraction and Second-Order Doppler Effect". Mössbauer Effect in Lattice Dynamics. John Wiley & Sons. doi:10.1002/9783527611423.ch5. ISBN 978-3-527-61142-3.
  16. ^ Martinho, Marlène; Münck, Eckard (2010). "57Fe Mössbauer Spectroscopy in Chemistry and Biology". Physical Inorganic Chemistry. pp. 39–67. doi:10.1002/9780470602539.ch2. ISBN 9780470602539.
  17. ^ Schuenemann, V.; Paulsen, H. (2007-12-10). "Moessbauer spectroscopy". In Scott, Robert A.; Lukehart, Charles M. (eds.). Applications of Physical Methods to Inorganic and Bioinorganic Chemistry. ISBN 978-0-470-03217-6.
  18. ^ Costas, Miquel; Mehn, Mark P.; Jensen, Michael P.; Que, Lawrence (1 February 2004). "Dioxygen activation at mononuclear nonheme iron active sites: enzymes, models, and intermediates". Chemical Reviews. 104 (2): 939–986. doi:10.1021/CR020628N. ISSN 0009-2665. PMID 14871146. S2CID 33300052. Wikidata Q35660894.
  19. ^ Klingelhöfer, G.; et al. (2002). "The miniaturized Mössbauer spectrometer MIMOS II for extraterrestrial and outdoor terrestrial applications: A status report". Hyperfine Interactions. 144 (1–4): 371–379. Bibcode:2002HyInt.144..371K. doi:10.1023/A:1025444209059. S2CID 94640811.
  20. ^ 뫼스바우어 효과 데이터 센터 20.08.2013

외부 링크