분자 진동

분자진동은 분자의 질량중심이 변하지 않도록 분자의 원자가 서로 상대적인 주기적인 운동이다.일반적인 진동 주파수는 10Hz 미만에서¹³ 약¹⁴ 10Hz까지이며, 약 300~3000cm의⁻¹ 파장과 약 30~3µm의 파장에 해당합니다.

는 이원자 분자 A−B 들어, sec−1의 진동 주파수 ν x12π k({\displaystyle \nu){1\over{2\pi}}{\sqrt{k\over \mu}}}, dyne/cm 또는 erg/cm2과 μ에서, k는 힘의 상수는 환산 질량 1μ에 의해 주어진다=1mA+1mB{\displaystyle{\frac{1}{\mu}}={\frac{1}{m_{A $}}+{\frac$ { $1}{m_{$ B ${\frac {1}{\mu }}={\frac {1}{m_{A}}}+{\frac {1}{m_{B}}}$ cm 단위의⁻¹ 진동파수는 ${\tilde {\nu }}\;={1 \over {2\pi c}}{\sqrt {k \over \mu }},$ ~ $=$ ${\tilde {\nu }}\;={1 \over {2\pi c}}{\sqrt {k \over \mu }},$ ${\tilde {\nu }}\;={1 \over {2\pi c}}{\sqrt {k \over \mu }},$ ${\tilde {\nu }}\;={1 \over {2\pi c}}{\sqrt {k \over \mu }},$ ${\displaystyle {tilde {2\pi$ c $}}{\displayrt {k \over \mu$ }}}입니다 ${\tilde {\nu }}\;={1 \over {2\pi c}}{\sqrt {k \over \mu }},$ .여기서 c는 cm/sec 단위의 광속입니다.

다원자 분자의 진동은 서로 독립적인 정상 모드로 설명되지만, 각 정상 모드는 분자의 다른 부분의 동시 진동을 포함합니다.일반적으로 N개의 원자를 가진 비선형 분자는 3N~6개의 정상적인 진동 모드를 가지지만, 선형 분자는 분자축에 대한 회전을 관찰할 ^[1]수 없기 때문에 3N~5개의 모드를 가진다.이원자 분자는 하나의 정상적인 진동 형태를 가지고 있는데, 왜냐하면 그것은 단일 결합을 늘리거나 압축할 수 있기 때문이다.

분자진동은 분자가 δE=hθ(h는 플랑크 상수)의 관계에 따라 진동 주파수 δE에 대응하는 에너지 δE를 흡수할 때 들뜨게 된다.이러한 에너지의 양자 중 하나가 지면 상태에서 분자에 흡수될 때 기본 진동이 발생한다.여러 퀀텀이 흡수되면 첫 번째 이상의 음색이 들뜨게 됩니다.

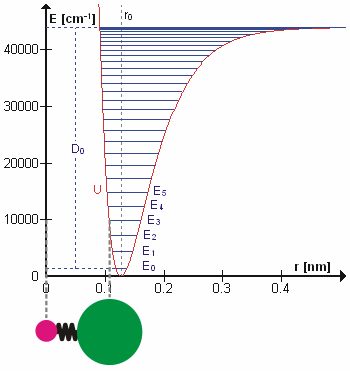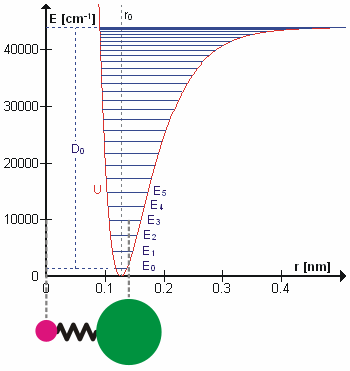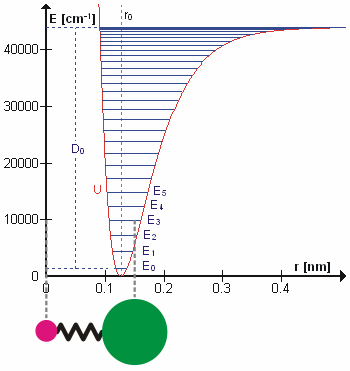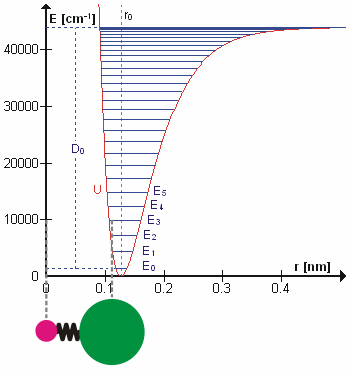
제1의 근사치에서는 통상진동에서의 운동은 일종의 단순한 고조파 운동이라고 할 수 있다.이 근사치에서 진동 에너지는 원자 변위에 관한 2차 함수(포물선)이며, 첫 번째 오버톤은 기본 주파수의 2배를 가진다.실제로는 진동은 부조화이며 첫 번째 오버톤은 기본의 두 배보다 약간 낮은 주파수를 가집니다.높은 음색의 들뜸은 점차적으로 더 적은 추가 에너지를 포함하며, 분자의 잠재적 에너지는 모스 전위 또는 더 정확하게 모스/장거리 전위에 가깝기 때문에 결국 분자의 해리로 이어집니다.

분자의 진동 상태는 다양한 방법으로 조사될 수 있다.가장 직접적인 방법은 적외선 분광법을 사용하는 것이다. 진동 전이에는 일반적으로 스펙트럼의 적외선 영역에 해당하는 양의 에너지가 필요하기 때문이다.일반적으로 가시광선을 사용하는 라만 분광법을 사용하여 진동 주파수를 직접 측정할 수도 있습니다.두 기술은 상호 보완적이며, 둘 사이의 비교는 중심대칭 분자에 대한 상호 배제 규칙의 경우와 같은 유용한 구조 정보를 제공할 수 있다.

진동 들뜸은 자외선이 보이는 영역의 전자 들뜸과 함께 발생할 수 있습니다.결합된 들뜸은 진동자 천이(vibronic transition)로 알려져 전자 천이, 특히 기체 상태의 분자에 진동 미세 구조를 제공합니다.

진동과 회전을 동시에 들뜨게 하면 진동 회전 스펙트럼이 생긴다.

진동 모드 수

N개의 원자를 $가진$ 분자는 N개의 모든 $핵$ 의 위치가 총 3N좌표에 의존하기 때문에 번역, 회전, 진동을 포함한 3N자유도를 갖는다.변환은 3개의 데카르트 좌표로 위치를 설명할 수 있는 질량 중심 이동에 해당합니다.

비선형 분자는 서로 수직인 3개의 축 중 하나를 회전시킬 수 있으며, 따라서 3개의 회전 자유도를 가진다.선형 분자의 경우, 분자 축에 대한 회전은 원자핵의 움직임을 포함하지 않기 때문에 원자 ^[2]^[3]좌표를 바꿀 수 있는 2개의 회전 자유도만 있습니다.

선형 분자의 회전이 공간에서의 분자축의 방향을 변화시킨다는 것도 같은 주장으로 위도와 경도에 대응하는 2개의 좌표로 설명할 수 있다.비선형 분자의 경우 한 축의 방향이 이들 2개의 좌표로 설명되며, 이 축 주위의 분자의 방향은 제3의 회전 ^[4]좌표를 제공한다.

따라서 진동 모드의 수는 3N에서 변환 및 회전 자유도를 뺀 값 또는 선형 분자의 경우 3N–5, 비선형 ^[2]^[3]^[4]분자의 경우 3N–6이다.

진동 좌표

정상적인 진동의 좌표는 분자 내 원자의 위치변화의 조합이다.진동이 들뜨면 좌표가 진동수인 주파수 $θ$ 에 따라 정현적으로 변화합니다.

내부 좌표

내부 좌표는 평면 분자 에틸렌과 관련하여 다음과 같은 유형이다.

스트레칭: C–H 또는 C–C와 같은 결합 길이의 변화
굽힘 : 메틸렌기 내 HCH 각도와 같이 두 결합 사이의 각도의 변화
흔들림: 메틸렌 그룹과 분자의 나머지 부분과 같은 원자 그룹 사이의 각도 변화.
흔들림: 메틸렌기와 같은 원자 그룹의 평면과 분자의 나머지 부분을 통과하는 평면 사이의 각도의 변화.
비틀림: 두 개의 원자 그룹 사이의 각도의 변화, 예를 들어 두 개의 메틸렌 그룹 간의 각도의 변화.
면외: C-H 결합 중 하나와 에틸렌 분자의 나머지 원자에 의해 정의된 평면 사이의 각도 변화.또 다른 예는 붕소 원자가 3개의 불소 원자의 평면을 드나들 때 BF입니다₃.

흔들림, 흔들림, 흔들림 또는 비틀림 등은 관련된 그룹 내의 결합 길이를 변경하지 않는다.각도가 그래요.흔들림은 군 내 원자가 같은 평면에 있다는 점에서 흔들림과 구별된다.

에틸렌에는 12개의 내부 좌표가 있습니다: 4개의 C–H 스트레칭, 1개의 C–C 스트레칭, 2개의 H–C–H 벤딩, 2CH₂ 흔들림, 2CH₂ 흔들림, 1개의 비틀림.각 탄소 원자의 각도가 동시에 증가할 수 없기 때문에 H-C-C 각도는 내부 좌표와 H-C-H 각도로 사용할 수 없습니다.

이러한 좌표는 일반 모드에 해당하지 않습니다(#정상 좌표 참조).즉, 특정 주파수나 진동 천이에는 대응하지 않습니다.

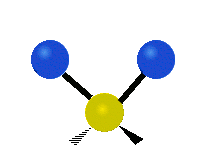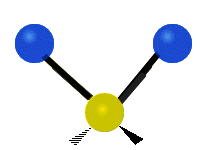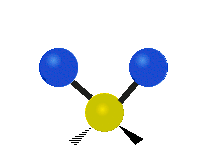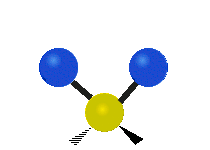
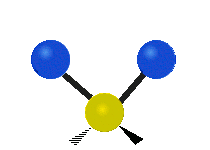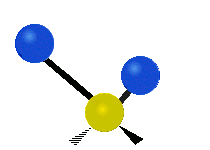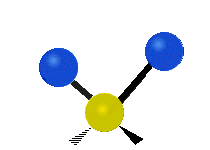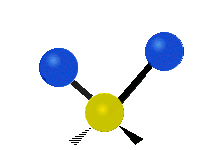
설명을 위한 분자 내 메틸렌기(–CH₂–)의 진동

유기 화합물에서 흔히 볼 수 있는 CH 그룹₂ 내에서는 두 개의 저질량 수소가 여섯 가지 다른 방식으로 진동할 수 있으며, 이는 세 쌍의 모드로 분류될 수 있습니다: 1. 대칭 및 비대칭 스트레칭, 2. 가위질, 3. 흔들림, 3. 흔들림 및 비틀림.다음은 다음과 같습니다.

대칭 스트레칭	비대칭 스트레칭	가위질(굽힘)

흔들리다	흔들리다	비틀림

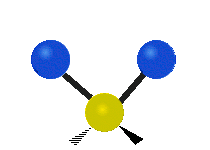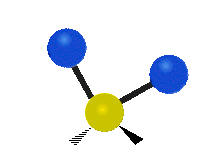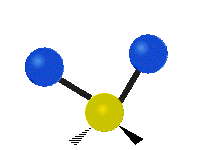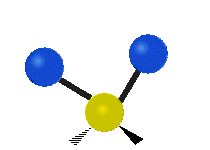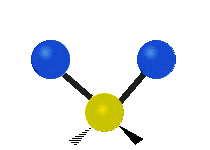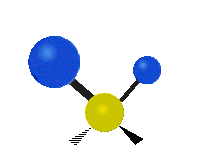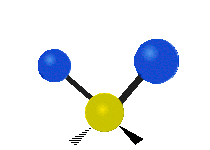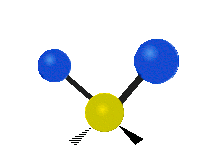(이 그림들은 분자의 전체적인 움직임의 균형을 맞추기 위해 반드시 나타나지만, 가벼운 H 원자의 움직임보다 훨씬 작은 C 원자의 "재코일"을 나타내지 않는다.)

대칭 적응 좌표

대칭 적응 좌표는 일련의 내부 ^[5]좌표에 투영 연산자를 적용하여 생성할 수 있습니다.투영 연산자는 분자 점 그룹의 문자 표의 도움을 받아 구성됩니다.예를 들어, 에텐 분자의 4개의 (비정규화) C-H 스트레칭 좌표는 다음과 같이 주어진다.

Q_{s1}=q_{1}+q_{2}+q_{3}+q_{4}}\!

Q_{s2}=q_{1}+q_{2}-q_{3}-q_{4}\!

Q_{s3}=q_{1}-q_{2}+q_{3}-q_{4}\!

Q_{s4}=q_{1}-q_{2}-q_{3}+q_{4}}\!

$q_{1}-q_{4}$ 서 $q_{1}-q_{4}$ $q_{1}-q_{4}$ - $q_{1}-q_{4}$ 4({ $displaystyle q_{1}-q_{4})$ 는 $q_{{1}}-q_{{4}}$ 4개의 C-H 결합 각각을 늘리기 위한 내부 좌표입니다.

대부분의 작은 분자에 대한 대칭 적응 좌표의 그림은 ^[6]나카모토에서 찾을 수 있다.

정상 좌표

Q로 표시된 정상 좌표는 정상적인 진동 모드와 관련하여 평형 위치에서 떨어진 원자의 위치를 나타냅니다.각 정상 모드에는 하나의 정상 좌표가 할당되므로 정상 좌표는 항상 해당 정상 모드를 따라 진행되는 "진행"을 참조합니다.형식적으로 정규 모드는 영속적인 결정식을 풀어서 결정되며, 그 후 정규 좌표는 (정규 모드에 걸쳐) 데카르트 좌표에 대한 합계로 표현될 수 있다.정상 모드는 분자 진동을 지배하는 매트릭스를 대각선으로 하여 각 정상 모드가 독립적인 분자 진동이 되도록 합니다.만약 분자가 대칭을 가지고 있다면, 정규 모드는 그것의 점군 아래에서 환원 불가능한 표현을 "변환"한다.정규 모드는 그룹 이론을 적용하고 축소할 수 없는 표현을 데카르트 좌표에 투영함으로써 결정됩니다.예를 들어 이 처리를 CO에₂ 적용하면 C=O 스트레칭은 독립적이지 않고 O=C=O 대칭 스트레칭과 O=C=O 비대칭 스트레칭이 있음을 알 수 있다.

대칭 스트레칭: 2개의 C–O 스트레칭 좌표의 합계. 2개의 C–O 결합 길이가 같은 양으로 변화하고 탄소 원자는 정지합니다.Q = q₁ + q₂
비대칭 스트레칭: 2개의 C-O 스트레칭 좌표의 차이입니다.한쪽은 C-O 결합 길이가 증가하고 다른 한쪽은 감소합니다.Q = q₁ - q₂

두 개 이상의 정규 좌표가 분자 점군의 동일한 축소 불가능한 표현에 속할 경우(즉, 동일한 대칭을 가진다), "혼합"이 존재하며 조합의 계수를 선험적으로 결정할 수 없다.예를 들어, 선형 분자 시안화 수소, HCN에서, 두 개의 스트레칭 진동은

주로 약간의 C–N 스트레칭을 수반하는 C–H 스트레칭; Q₁ = q₁ + a q₂ (a < 1)
주로 약간의 C–H 스트레칭을 수반하는 C–N 스트레칭. Q₂ = b₁ q₂ + q (b < < 1)

계수 a와 b는 Wilson GF ^[7]방법을 사용하여 완전 정규 좌표 분석을 수행하여 구합니다.

뉴턴 역학

에너지 레벨₃ E.D₀.에서 진동하는 비조화 발진기로서의 HCl 분자는 여기서 해리 에너지, rbond₀ 길이, U 위치 에너지입니다.에너지는 파도로 표현된다.염화수소 분자는 곡선상의 결합 길이 변화를 보여주기 위해 좌표계에 부착됩니다.

아마도 놀랍게도, 분자 진동은 뉴턴 역학을 이용하여 정확한 진동 주파수를 계산해 낼 수 있다.기본적인 가정은 각 진동이 스프링에 해당하는 것처럼 취급할 수 있다는 것입니다.고조파 근사에서 스프링은 후크의 법칙을 따릅니다. 즉, 스프링을 연장하는 데 필요한 힘은 연장에 비례합니다.비례 상수는 힘 상수 k로 알려져 있습니다.비조화 진동자는 다른 곳에서 ^[8]고려됩니다.

\mathrm {F} =-kQ\!

뉴턴의 운동 제2법칙에 따르면 이 힘은 감소된 질량, μ 곱하기 가속도와 같습니다.

\displaystyle \mathrm {F} =\mu {frac {d^{2}Q}{dt^{2}}}

이것은 하나의 힘이고 같은 힘이기 때문에 일반 미분 방정식이 따릅니다.

{\displaystyle\mu{d^{2}Q}{dt^{2}}+kQ=0}

이 단순한 고조파 운동 방정식의 해답은

\displaystyle Q(t)=A\cos(2\pi \nu t);\nu ={1 \over {2\pi }}{\displayrt {k \over \mu }}.\!}

A는 진동 좌표 Q의 최대 진폭입니다.환원 질량 μ를 정의하는 것이 남는다.일반적으로, 이원자 분자 AB의 감소된 질량은 원자 질량_A m과_B m의 관점에서 다음과 같이 표현된다.

({displaystyle {\frac {1}{\mu }}=squalfrac {1}{m_{A}}+{\frac {1}{m_{B}}}).}

감소된 질량을 사용하면 분자의 질량 중심이 진동의 영향을 받지 않습니다.고조파 근사에서 분자의 위치 에너지는 법선 좌표의 2차 함수이다.따라서 힘-상수는 위치 에너지의 2차 도함수와 같다.

k=frac {\partial Q^{2}}

두 개 이상의 정상 진동이 동일한 대칭을 가질 경우 완전한 정상 좌표 분석을 수행해야 합니다(GF 방법 참조).진동주파수 θ는_i 행렬곱 GF의 고유값 θ에서_i 구한다.G는 원자의 질량과 ^[7]분자의 기하학적 구조에서 도출된 숫자의 행렬이다.F는 힘 상수 값에서 도출된 행렬이다.고유값 결정에 대한 자세한 내용은 ^[9]에서 확인할 수 있습니다.

양자역학

고조파 근사에서 전위 에너지는 정규 좌표의 2차 함수입니다.슈뢰딩거 파동 방정식을 풀면, 각 정상 좌표에 대한 에너지 상태는 다음과 같이 주어진다.

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

n

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

(

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

+

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

)

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

(

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

+

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

2

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

)

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

2

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

m ( \

display style

E _ { n }

= h

\

left

(

n

+ {

1

\

over

2 } \

right

) \

nu =

h \ left

（

n + { 2

over

2

E_{n}=h\left(n+{1 \over 2}\right)\nu =h\left(n+{1 \over 2}\right){1 \over {2\pi }}{\sqrt {k \over m}}\!

\ right

}

), m!

여기서 n은 0, 1, 2의 값을 취할 수 있는 양자수입니다.여러 종류의 분자 에너지가 연구되고 여러 개의 양자수가 사용되는 분자 분광학에서, 이 진동 양자수는 종종 ^[10]^[11]v로 지정된다.

따라서 n(또는 v)이 1만큼 변화했을 때의 에너지 차이는 플랑크 상수와 고전 역학을 사용하여 도출된 진동 주파수의 곱인 h $h\nu$ {\(\ $displaystyle$ h $\nu$ 와 같다.광자의 흡수에 의한 레벨 n에서 레벨 n+1로의 이행의 경우, 광자의 주파수는 (조화 진동자 근사에서) 고전적인 진동 주파수 $\nu$ (\ $displaystyle \nu)$ 와 같다.

특정 선택 규칙을 공식화할 수 있는 첫 번째 5개 파동 함수의 그래프는 양자 조화 진동자를 참조하십시오.예를 들어, 고조파 발진기 전환은 양자수 n이 1만큼 변화할 때만 허용됩니다.

\displaystyle \Delta n=\pm 1

그러나 이는 비조화 진동자에는 적용되지 않으며, 진동은 비조화이기 때문에 오버톤을 관찰할 수 있습니다.부조화의 또 다른 결과는 상태 n=2와 n=1 사이의 전환이 지면 상태와 첫 번째 들뜬 상태 사이의 전환보다 약간 적은 에너지를 갖는다는 것이다.이러한 전환은 핫 밴드를 발생시킨다.비조화 발진기의 진동 레벨을 설명하기 위해 던햄 확장을 사용합니다.

강도

적외선 스펙트럼에서 흡수 대역의 세기는 정규 ^[12]좌표에 대한 분자 쌍극자 모멘트의 도함수에 비례한다.마찬가지로, 라만 대역의 세기는 정규 좌표에 대한 편광률의 도함수에 의존합니다.또한 사용되는 레이저 파장의 4제곱에 의존합니다.

「」를 참조해 주세요.

레퍼런스

^ Landau, L. D.; Lifshitz, E. M. (1976). Mechanics (3rd ed.). Pergamon Press. ISBN 0-08-021022-8.
^ ^a ^b Hollas, J. M. (1996). Modern Spectroscopy (3rd ed.). John Wiley. p. 77. ISBN 0471965227.
^ ^a ^b Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of Molecular Spectroscopy (4th ed.). McGraw Hill. p. 71. ISBN 0-07-707976-0.
^ ^a ^b Atkins, P. W.; Paula, J. de (2006). Physical Chemistry (8th ed.). New York: W. H. Freeman. p. 460. ISBN 0716787598.
^ Cotton, F. A. (1971). Chemical Applications of Group Theory (2nd ed.). New York: Wiley. ISBN 0471175706.
^ Nakamoto, K. (1997). Infrared and Raman spectra of inorganic and coordination compounds, Part A (5th ed.). New York: Wiley. ISBN 0471163945.
^ ^a ^b Wilson, E. B.; Decius, J. C.; Cross, P. C. (1995) [1955]. Molecular Vibrations. New York: Dover. ISBN 048663941X.
^ Califano, S. (1976). Vibrational States. New York: Wiley. ISBN 0471129968.
^ Gans, P. (1971). Vibrating Molecules. New York: Chapman and Hall. ISBN 0412102900.
^ Hollas, J. M. (1996). Modern Spectroscopy (3rd ed.). John Wiley. p. 21. ISBN 0471965227.
^ Atkins, P. W.; Paula, J. de (2006). Physical Chemistry (8th ed.). New York: W. H. Freeman. pp. 291 and 453. ISBN 0716787598.
^ Steele, D. (1971). Theory of vibrational spectroscopy. Philadelphia: W. B. Saunders. ISBN 0721685803.

추가 정보

Sherwood, P. M. A. (1972). Vibrational Spectroscopy of Solids. Cambridge University Press. ISBN 0521084822.

외부 링크

[1] Landau, L. D.; Lifshitz, E. M. (1976). Mechanics (3rd ed.). Pergamon Press. ISBN 0-08-021022-8.

[Hollas77-2] Hollas, J. M. (1996). Modern Spectroscopy (3rd ed.). John Wiley. p. 77. ISBN 0471965227.

[Banwell-3] Banwell, Colin N.; McCash, Elaine M. (1994). Fundamentals of Molecular Spectroscopy (4th ed.). McGraw Hill. p. 71. ISBN 0-07-707976-0.

[Atk460-4] Atkins, P. W.; Paula, J. de (2006). Physical Chemistry (8th ed.). New York: W. H. Freeman. p. 460. ISBN 0716787598.

[Cotton-5] Cotton, F. A. (1971). Chemical Applications of Group Theory (2nd ed.). New York: Wiley. ISBN 0471175706.

[Nakamoto-6] Nakamoto, K. (1997). Infrared and Raman spectra of inorganic and coordination compounds, Part A (5th ed.). New York: Wiley. ISBN 0471163945.

[WilsonDeciusCross-7] Wilson, E. B.; Decius, J. C.; Cross, P. C. (1995) [1955]. Molecular Vibrations. New York: Dover. ISBN 048663941X.

[Califano-8] Califano, S. (1976). Vibrational States. New York: Wiley. ISBN 0471129968.

[Gans-9] Gans, P. (1971). Vibrating Molecules. New York: Chapman and Hall. ISBN 0412102900.

[10] Hollas, J. M. (1996). Modern Spectroscopy (3rd ed.). John Wiley. p. 21. ISBN 0471965227.

[11] Atkins, P. W.; Paula, J. de (2006). Physical Chemistry (8th ed.). New York: W. H. Freeman. pp. 291 and 453. ISBN 0716787598.

[Steele-12] Steele, D. (1971). Theory of vibrational spectroscopy. Philadelphia: W. B. Saunders. ISBN 0721685803.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

v t 분광학
진동	FT-IR 라만 공명 라만 회전 회전 진동 진동 진동원형 이색성 핵공명진동분광학
UV-Vis-NIR	자외선-가시 가능 형광 바이브로닉 근적외선 REMPI(Resonance Enhanced Multiphoton Ionization) 라만 광학 활성 분광법 라만 분광학 레이저에 의해 유도되다
X-ray 및 광전자	에너지 분산형 X선 분광법 광전자 아토믹 배출. X선 광전자 분광법 EXAFS
핵자	감마 뫼스바우어
라디오웨이브	NMR 테라헤르츠 ESR/EPR 강자성 공명
다른이들	음향 공명 분광법 오거 분광법 천체 분광학 캐비티 링다운 분광법 원형 이색성 분광법 코히런트 반스토크스 라만 분광법 냉증기 원자 형광 분광법 변환전자 뫼스바우어 분광법 상관분광학 심층 과도 분광법 이중 편파 간섭계 전자현상분광학 EPR 분광법 힘분광학 푸리에 변환 분광법 글로 방전 광학 발광 분광법 하드론 분광법 초분광 이미징 비탄성 전자 터널링 분광법 비탄성 중성자 산란 레이저에 의한 파괴 분광법 뫼스바우어 분광법 중성자 스핀 에코 광음향 분광법 광방출 분광법 광열 분광법 펌프-프로브 분광법 포화 분광학 주사 터널링 분광법 분광 광도 측정 시간 분해 분광법 타임 스트레치 열적외선 분광법 비디오 분광법 선형 분자의 진동 분광법
카테고리 공통

Search

분자 진동

네임스페이스

더

목차

진동 모드 수