양자 스핀 액체

Quantum spin liquid

응집 물질 물리학에서 양자 스핀 액체는 특정 자성 물질에서 양자 스핀을 상호 작용시킴으로써 형성될 수 있는 물질의 상이다.양자 스핀 액체(QSL)는 일반적으로 장거리 양자 얽힘, 부분화된 들뜸 및 일반 자기 [1]순서가 없는 것이 특징이다.

양자 스핀 액체 상태는 1973년 물리학자 필 앤더슨이 가장 가까운 이웃과 반강자적으로 상호작용하는 삼각 격자상의 스핀 시스템의 기저 상태로 처음 제안했습니다. 즉, 이웃 스핀이 반대 [2]방향으로 정렬되도록 합니다.1987년 앤더슨이 무질서한 [3][4]스핀-액체 상태의 관점에서 고온 초전도 현상을 설명하는 이론을 제안했을 때 양자 스핀 액체는 더욱 관심을 불러일으켰다.

기본 속성

자력 저하로 인해 발생하는 스핀 액체의 예

가장 간단한 종류의 자기상은 파라자넷으로, 각각의 개별 스핀은 이상적인 기체의 원자처럼 나머지 스핀과 독립적으로 작용합니다.이 고도로 무질서한 단계는 고온에서 자석의 일반적인 상태이며, 열적 변동이 지배적입니다.냉각 시 스핀은 종종 강자석(또는 반강자석) 단계로 진입합니다.이 단계에서는 스핀 간의 상호 작용으로 인해 스핀이 도메인, 스트라이프 또는 체커보드와 같은 대규모 패턴으로 정렬됩니다.이러한 장거리 패턴은 "자기 질서"라고 불리며, 많은 [5]고체로 형성된 규칙적인 결정 구조와 유사합니다.

양자 스핀 액체는 이러한 전형적인 행동에 대한 극적인 대안을 제공합니다.이 상태에 대한 직관적인 설명은 강자성 스핀 상태와 비교하여 [6]무질서 스핀의 "액체"로, 결정 얼음에 비해 액체 상태의 물이 무질서 상태인 것과 매우 유사하다.그러나 다른 무질서 상태와는 달리, 양자 스핀 액체 상태는 무질서를 매우 낮은 [7]온도로 보존합니다.양자 스핀 액체의 보다 현대적인 특성에는 위상 순서,[8] 장거리 양자 얽힘 특성 [1]및 임의 [9]들뜸이 포함됩니다.

예

몇몇 물리적 모델은 양자 스핀 액체로 설명할 수 있는 무질서한 지면 상태를 가지고 있습니다.

좌절된 자기 모멘트

당황한 이징은 삼각형을 돌린다.

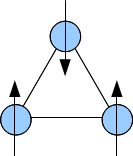
국소 스핀은 동시에 모든 것을 만족시킬 수 없는 경쟁적인 교환 상호작용이 있을 경우 좌절되어 시스템의 접지 상태가 크게 퇴화됩니다.반강자적으로 상호작용하는 아이싱 스핀의 삼각형(스핀의 가능한 방향은 "위" 또는 "아래"뿐이라는 의미)은 좌절의 간단한 예입니다.그라운드 상태에서는 스핀 중 2개는 반평행이 될 수 있지만 3번째 스핀은 반평행이 될 수 없다.이로 인해 접지 상태에서 스핀의 가능한 방향(이 경우 6개)이 증가하여 변동을 개선하여 자기 순서를 억제할 수 있습니다.

공명 원자가 결합(RVB)

주요 기사:공명 원자가 결합 이론
원자가 결합이 단단해결합은 특정 패턴을 형성하며 얽힌 스핀 쌍으로 구성됩니다.

자기 모멘트가 없는 접지 상태를 구축하기 위해 반강자성 상호작용에 의해 2개의 전자 스핀이 스핀 0 싱글트를 형성하는 원자가 결합 상태를 사용할 수 있습니다.시스템의 모든 스핀이 이와 같이 결합되어 있으면 시스템 전체의 상태도 스핀 0을 가지며 비자성입니다.결합을 형성하는 두 스핀은 다른 스핀과 얽히지 않으면서 최대한 얽혀 있습니다.모든 스핀이 특정 국소 정적 결합에 분포하는 경우, 이를 원자가 결합 고체(VBS)라고 합니다.

VBS와 스핀 액체를 구별하는 두 가지가 있습니다.우선 일정한 순서로 결합을 배열함으로써 격자대칭이 깨지는 것이 일반적이지만 스핀액에는 해당되지 않는다.둘째, 이 지상 상태는 장기적인 얽힘이 없다.이를 달성하기 위해서는 원자가 결합의 양자역학적 변동이 허용되어야 하며, 이로 인해 스핀의 많은 다른 분할이 원자가 결합으로 중첩되는 지면 상태가 된다.분할이 균등하게 분포되어 있는 경우(양자 진폭이 동일), 특정 분할("가 결합 액체")에 대한 선호는 없습니다.이러한 종류의 지상 상태 파동 함수는 1973년 P. W. Anderson에 의해[2] 스핀 액체의 지상 상태로 제안되었으며 공명 원자가 결합(RVB) 상태라고 불립니다.이러한 상태는 고온 초전도체 [4]물리학에서 중요한 역할을 하도록 제안되었기 때문에 이론적으로 큰 관심을 끌고 있습니다.

  • One possible short-range pairing of spins in a RVB state.

    RVB 상태에서 스핀의 단거리 페어링이 가능합니다.

  • Long-range pairing of spins.

    스핀의 장거리 페어링.

들뜸

스피논이 액체 속에서 움직인다.

원자가 결합은 가장 가까운 이웃에 의해서만 형성될 필요는 없으며, 그 분포는 재료에 따라 다를 수 있다.원자가 결합의 기여도가 큰 지면 상태는 원자가 결합을 분해하기 쉽기 때문에 낮은 에너지 스핀 들뜸을 가진다.브레이크 시, 그들은 두 개의 자유 회전을 형성한다.다른 들뜸은 원자가 결합을 재정렬시켜 단거리 결합에서도 낮은 에너지 들뜸을 일으킨다.스핀 액체에 대한 매우 특별한 점은 그들이 이국적인 들뜸을 지원한다는 것이다. 즉, 소수 양자수를 가진 들뜸을 의미한다.대표적인 예는 전하 중성이며 S S를 전달하는 스피논의 들뜸입니다. 스핀 액체의 경우 스핀 하나가 원자가 결합에서 쌍을 이루지 않으면 스피논이 생성됩니다.그것은 낮은 에너지 비용으로 근처의 원자가 채권을 재배치함으로써 이동할 수 있다.

(안정적인) RVB 상태 실현

RVB 그림을[10] 사용한 사각 격자의 RVB 상태에 대한 첫 번째 논의에서는 서로 다른 하위 격자를 연결하는 가장 가까운 인접 결합만 고려한다.생성된 RVB 상태는 모든 근접 인접 결합 구성의 동일한 진폭 중첩입니다.이러한 RVB 상태에는 스핀 등을 구속할 수 있는 비상 U () {U (1} 게이지 필드가 포함되어 있는 것으로 생각됩니다.따라서 정사각형 격자의 등진폭 가장 가까운 RVB 상태는 불안정하며 양자 스핀 위상에 해당하지 않습니다.두 안정적인 위상 사이의 임계 위상 전이 지점을 나타낼 수 있습니다.안정적이고 분리된 스피논을 포함하는 RVB 상태의 버전은 키랄 스핀 상태입니다.[11][12]나중에 스핀온이 분리된 안정적인 RVB 상태의 또 다른 버전인 Z2 스핀 액체가 제안되며, 이는[14] 가장 단순한 위상 순서인 Z2 위상 순서를 실현한다.키랄 스핀 상태와 Z2 스핀 액체 상태 모두 동일한 서브 래티스를 연결하는 긴 RVB 결합을 가집니다.키랄 스핀 상태에서는 서로 다른 결합 구성이 복잡한 진폭을 가질 수 있지만, Z2 스핀 액체 상태에서는 서로 다른 결합 구성이 실제 진폭만 가질 수 있습니다.삼각형 격자의 RVB 상태에서도 Z2 스핀 [15]액체가 실현됩니다.이 경우 다른 결합 구성은 실제 진폭만 가집니다.토릭 코드 모델은 스핀 회전 대칭을 명백히 깨뜨리고 정확하게 [16]용해되는 Z2 스핀 액체(및 Z2 위상 순서)의 또 다른 구현입니다.

실험용 시그니처와 프로브

물질을 스핀 액체로 식별하는 단일 실험 특성이 없기 때문에 스핀 액체를 특징짓는 다른 특성에 대한 정보를 얻기 위해 여러 가지 실험을 수행해야 합니다.[17]

자화율

고온의 고전적인 파라자넷 단계에서는 퀴리에 의해 자화율이 주어진다.바이스의 법칙

이 방정식에 실험 데이터를 적합시키면 현상학적 퀴리가 결정된다.Weiss 온도, C { \_ { } 。두 번째 인T c { T{ c} χ T의 비분석적 특징에서 알 수 있듯이 재료의 자기 순서가 발생하기 시작하는 T c { T _ { c } } the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the

전형적인 antiferromagnet에서 두 온도와)f 주세요. 이상적인 양자 스핀 액체 어떤 온도(Tc)0){\displaystyle(T_{c}=0)}에 큰 .[18]→ ∞{\displaystyle f\to\infty}는diverging 좌절 매개 변수 f을 것이다 자기 질서를 구연하지 않을 것 1{\displaystyle f=1}일치해야 한다. valu e f> { f > }은 가능한 스핀액상을 나타냅니다.격자 구조가 다른 일부 불만 재료와 퀴리-아래 [7]표에 Weiss 온도를 나타냅니다.모두 스핀 액체 후보입니다.

재료. 격자
γ-(BEDT-TTF2)2Cu(CN)3 이방성 삼각 -375
ZnCu3(OH)6Cl2(허버트미사이트) 카고메 -241
BaCuVO328(OH)(2베지니라이트) 카고메
Na4Ir3O8 하이퍼카고메 -650
PbCuTe2O6 하이퍼카고메 -22 [19]
Cu-(1,3-벤젠디카르본산염) 카고메 -33 [20]
Rb2Cu3SnF12 카고메 [21]
1T-TaaS2 삼각형의

다른.

자기 순서가 없다는 가장 직접적인 증거 중 하나는 NMR 또는 μSR 실험입니다.국부 자기장이 존재하는 경우 핵 스핀 또는 뮤온 스핀에 영향을 미쳐 측정할 수 있습니다.γ-(BEDT-TTF)2Cu2(CN)3에 대한 1H-NMR 측정 결과, 이 화합물 내 인접 스핀 간 결합 상수 J250250K보다[23] 4배 작은 32mK까지 자기 순서가 나타나지 않았다.자세한 조사 내용은 다음과 같습니다.

  • 특정 열 측정은 이론 모델과 비교할 수 있는 상태의 낮은 에너지 밀도에 대한 정보를 제공한다.
  • 열수송 측정은 들뜸이 국소적인지 아니면 순회적인지를 판별할 수 있습니다.
  • 중성자 산란은 들뜸과 상관(예: 스피논)의 성질에 대한 정보를 제공한다.
  • 반사율 측정을 통해 스피논이 발견될 수 있으며, 스피논은 비상 게이지장을 통해 전자기장에 결합되어 멱함수법칙의 광전도성을 [24]발생시킵니다.
Herbertsmithite, 지표 상태가 QSL 성질을 가진 것으로 판명된 광물

후보 자료

RVB 타입

삼각격자상의 스핀-1/2 반강자석인 클로로업레이트 CsCuCl의24 중성자 산란 측정 결과 확산 산란이 나타났다.이는 2D RVB [25]상태에서 발생하는 스피논에 기인했다.이후 이론 연구는 모든 실험 결과가 개별 [26]체인에 국한된 1D 스피논의 결과라고 주장하면서 이 그림에 도전장을 내밀었다.

그 후 2003년 [22]카노다 그룹의 유기 Mott 절연체(γ-(BEDT-TTF)2Cu2(CN))3에서 관찰되었다.스피논 페르미 표면을 가진 갭리스 스핀액(일명 균일한 RVB 상태)[2]에 해당할 수 있습니다.이 유기 양자 스핀 액체 화합물의 특이 위상도는 처음에 뮤온 스핀 [27]분광법을 사용하여 철저히 매핑되었다.

허버트미사이트

Herbertsmithite는 QSL 후보 [18]재료 중 가장 광범위하게 연구되고 있는 것 중 하나입니다.화학조성3 ZnCu(6OH2)Cl과 마름모꼴 결정구조를 가진 광물입니다.특히 이 구조 내의 구리 이온은 카고메 격자의 2차원 층을 형성한다.또한 산소 결합에 대한 초극변화로 인해 단일 층 내에서 1/ 스타일 /) 구리 스핀 간에 강한 반강자성 상호작용이 발생하지만 층 간 결합은 무시할 [18]수 있습니다.따라서 양자 스핀 [28][29]액체의 시제품 이론적인 예인 카고메 격자에서 반강자성 스핀 1/2 하이젠베르크 모델을 실현하는 것이 좋다.

합성 다결정 허버트미사이트 분말은 2005년에 처음 보고되었으며, 초기 자기 감수성 연구에서는 [30]2K까지 자기 질서의 징후는 보이지 않았다.후속 연구에서, 자기 질서의 부재는 50mK까지 확인되었고, 비탄성 중성자 산란 측정에서 낮은 에너지 스핀 들뜸의 광범위한 스펙트럼이 드러났으며, 저온 비열 측정에는 멱함수 법칙이 적용되었다.이를 통해 1/ S2스핀온 [31]들뜸이 있는 스핀 액체 상태에 대한 설득력 있는 증거가 제시되었습니다.O NMR과 [32]동적 자기 구조 [33]인자의 중성자 스펙트럼 분석을 포함한 광범위한 추가 실험을 통해 [34]2010년 현재 정확한 특성이 불분명하지만, 허버트미스타이트의 공극 없는 스핀 액체 물질로서의 식별이 강화되었다.

2011년에는 [35]대형(밀리미터 크기)의 허버트미사이트 단결정체가 성장하여 특징지어졌습니다.이를 통해 가능한 스핀 액체 특성을 보다 정확하게 측정할 수 있었습니다.특히 운동량 분해 비탄성 중성자 산란 실험은 광범위한 들뜸의 연속체를 보여주었다.이것은 틈이 없는 분수화된 스피논의 [36]증거로 해석되었다.후속 실험(O NMR과 고해상도, 저에너지 중성자 산란을 사용)은 이 그림을 다듬었고 실제로 0.07-0.09meV의 [37][38]작은 스피논 들뜸 갭이 있다는 것을 확인했다.

일부 측정치는 양자 임계 [39][40]행동을 암시했다.이 물질의 자기 응답은 벌크 AC 자화율과 낮은 에너지 동적 자화율 모두에서 스케일링 관계를 나타내며, 저온 열 용량은 [41][42]자기장에 크게 의존합니다.이 스케일링은 특정 양자 반강자석, 중연성 금속 및 2차원 He에서 양자 임계점에 [43]근접한 신호로 나타납니다.

2020년 허버트미사이트의 단결정 나노입자(~10nm)를 가스차 전기결정화를 이용해 상온에서 합성한 결과 스핀액성분이 이처럼 작은 [44]치수로 지속되고 있음을 알 수 있었다.

그림 1: 범례와 같이 서로 다른 자기장에서 YbRhSi의22 전자비열 C/T의 T의존성.B=8 Tesla에서 (C/T)max와max T의 값이 표시됩니다.최대(C/T)max는 자기장 B가 증가함에 따라 감소하지만max, T는 더 높은 T로 전환되어 B=18 Tesla에서 14K에 도달합니다.C/T~δ~M*을 관찰하면 그림 2와 같은 ZnCu3(OH)6Cl의2 SCQSL이 YbRhSi의22 중 페르미온과 같은 거동을 보인다는 결론을 내릴 수 있다.
그림 2: ZnCu3([41]OH)6Cl의2 다른 자기장에서의 자화율θ의 T의존성.B=7 Tesla에서 θ와maxmax T의 값이 표시된다.B=0에서의 T의존성(-2/3) T는 실선 곡선으로 표현된다.최대 δ(Tmax)는 자기장 B가 커짐에 따라 감소하는 반면max, T(B)는 B=14 Tesla에서 15K에 도달하는 더 높은 T로 전환됩니다.그림 1의 YbRhSi의 비열은22 θ~C/T~M*과 같은 성질을 보인다는 결론을 내렸다.따라서 ZnCu3(OH)6Cl의2 SCQSL은 YbRhSi의22 [46]무거운 페르미온으로 동작한다.

U(1)-디락 스핀액을 [47]실현할 수 있다.

키타예프 스핀 액체

2015년 8월 2차원 물질에서 양자 스핀 액체의 또 다른 증거가 관찰되었다.캠브리지 대학의 물리학자들과 독일 드레스덴에 있는 막스 플랑크 복합계 물리학 연구소의 연구진은, 마요라나 페르미온으로 알려진 이 분수 입자들의 첫 번째 신호를 그라와 유사한 구조의 2차원 물질로 측정했다.그들의 실험 결과는 키타예프 벌집 [48]모형으로 알려진 양자 스핀 액체에 대한 주요 이론 모델 중 하나와 성공적으로 일치했다.[49]

강상관 양자 스핀액

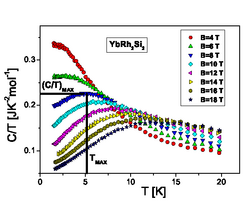
강상관 양자 스핀 액체(SCQSL)는 가능한 양자 스핀 액체(QSL)[7]의 구체적인 실현입니다.이는 중페르미온 금속의 특성을 가진 새로운 유형의 강상관 전기 절연체(SCI)를 나타냅니다.단, 전하의 흐름에 저항합니다.[46] [50] 저온 T에서 이 유형의 절연체의 비열은 T에 비례하며3, 열 용량이 T에 비례하는n 기존 절연체의 경우 n=3이 아닌 n이 1보다 작거나 같다.자기장 B가 SCI에 적용될 때 비열은 기존의 절연체와 달리 B에 강하게 의존합니다.SCI 후보는 몇 가지 있지만 그중에서 가장 유망한 것은 화학구조 ZnCu3(OH)6Cl을2 가진 광물인 허버트미사이트다.[50]

카고메형

CaCrO는10728 1K 미만에서도 장거리 질서가 발달하지 않고 간극 없는 들뜸의 스펙트럼이 확산된 카고메 2층 자석이다.

토릭 코드 타입

12월 2021년에는 원환체의 코드 형식의 양자 스핀 액체의 최초의 직접적인 측정이 두 팀:하나를 탐험하면서 땅 주와 양자 processor[53]과 다른 원자의 루비 격자 광 핀셋으로 양자 simu에에 수록된 이론적 blueprint[54]을 실행으로anyonic excitations이 성취했다 reported,[51][52]다.lator.[55]

특정 특성: 위상 페르미온 응축 양자 위상 전이

중 페르미온(HF) 금속과 2차원 헬륨-3에 대해 수집된 실험 사실은 준입자 유효 질량 M*이 매우 크거나 심지어 분산된다는 것을 보여준다.위상 페르미온 응축 양자상 전이(FCQ)PT)는 준입자를 보존하고 페르미 수준에서 평평한 에너지 띠를 형성합니다.FCQ의 등장PT는 유효질량 M*[43]의 무제한 성장과 직접 관련이 있으며 FCQPT 부근에서 M*은 온도 T, 수밀도 x, 자기장 B 및 압력 P 등의 기타 외부 파라미터에 의존하기 시작합니다.FCQ에서 유효 질량이 거의 일정하다는 가정에 기초한 란다우 패러다임과는 대조적으로PT 이론은 새로운 준입자의 유효 질량은 T, x, B 등에 크게 의존한다.따라서 FCQ를 기반으로 한 확장 준입자 패러다임에 동의/설명하기 위해PT를 도입해야 합니다.여기서 요점은 잘 정의된 준입자가 강하게 상관된 페르미 시스템의 열역학, 완화, 스케일링 및 수송 특성을 결정하며 M*은 T, x, B, P 등의 함수가 된다는 것이다.매우 다른 강한 상관관계가 있는 페르미 시스템에 대해 수집된 데이터는 보편적인 스케일링 동작을 보여줍니다; 다시 말해, 강한 상관관계가 있는 페르미온을 가진 다른 물질들은 예상외로 균일하게 판명되었습니다, 따라서 HF 금속, 준결정, 양자 스핀 액체, 2차원 헬륨-3, 그리고 com으로 구성된 물질의 새로운 상태를 형성합니다.고온의 [39][43]초전도성을 나타내는 파운드.

적용들

양자 스핀 액체 상태를 지원하는 재료는 데이터 저장 및 메모리에 응용될 수 있습니다.[56] 특히 스핀 액체 상태에 [57]의한 위상 양자 연산을 실현할 수 있다.양자 스핀 액체의 발전도 고온 초전도 [58]이해에 도움이 될 수 있다.

레퍼런스

  1. ^ a b Savary, L.; Balents, L. (2017). "Quantum spin liquids: a review". Reports on Progress in Physics. 80 (1): 016502. arXiv:1601.03742. Bibcode:2017RPPh...80a6502S. doi:10.1088/0034-4885/80/1/016502. PMID 27823986. S2CID 22285828.
  2. ^ a b c P. W. Anderson (1973). "Resonating valence bonds: A new kind of insulator?". Materials Research Bulletin. 8 (2): 153–160. doi:10.1016/0025-5408(73)90167-0.
  3. ^ Trafton, Anne (March 28, 2011). "A new spin on superconductivity?". MIT News. Retrieved 24 December 2012.
  4. ^ a b P. W. Anderson (1987). "The resonating valence bond state in La2CuO4 and superconductivity". Science. 235 (4793): 1196–1198. Bibcode:1987Sci...235.1196A. doi:10.1126/science.235.4793.1196. PMID 17818979. S2CID 28146486.
  5. ^ Chaikin, Paul M; Lubensky, Tom C (1995). Principles of Condensed-Matter Physics. Cambridge university press. ISBN 9780521432245.
  6. ^ Wilkins, Alasdair (August 15, 2011). "A Strange New Quantum State of Matter: Spin Liquids". io9. Retrieved 23 December 2012.
  7. ^ a b c Leon Balents (2010). "Spin liquids in frustrated magnets". Nature. 464 (7286): 199–208. Bibcode:2010Natur.464..199B. doi:10.1038/nature08917. PMID 20220838. S2CID 4408289.
  8. ^ Wolchover, Natalie (2018-01-03). "Physicists Aim to Classify All Possible Phases of Matter". Quanta Magazine. Retrieved 2019-05-05.
  9. ^ Wilczek, Frank (2017-02-28). "Inside the Knotty World of 'Anyon' Particles". Quanta Magazine. Retrieved 2019-05-05.
  10. ^ Kivelson, Steven A.; Rokhsar, Daniel S.; Sethna, James P. (1987). "Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity". Physical Review B. 35 (16): 8865–8868. Bibcode:1987PhRvB..35.8865K. doi:10.1103/physrevb.35.8865. PMID 9941277.
  11. ^ Kalmeyer, V.; Laughlin, R. B. (1987). "Equivalence of the resonating-valence-bond and fractional quantum Hall states". Physical Review Letters. 59 (18): 2095–2098. Bibcode:1987PhRvL..59.2095K. doi:10.1103/physrevlett.59.2095. PMID 10035416.
  12. ^ Wen, Xiao-Gang; Wilczek, F.; Zee, A. (1989). "Chiral Spin States and Superconductivity". Physical Review B. 39 (16): 11413–11423. Bibcode:1989PhRvB..3911413W. CiteSeerX 10.1.1.676.519. doi:10.1103/physrevb.39.11413. PMID 9947970.
  13. ^ Read, N.; Sachdev, Subir (1991). "Large-N expansion for frustrated quantum antiferromagnets". Physical Review Letters. 66 (13): 1773–1776. Bibcode:1991PhRvL..66.1773R. doi:10.1103/physrevlett.66.1773. PMID 10043303.
  14. ^ Wen, Xiao-Gang (1991). "Mean Field Theory of Spin Liquid States with Finite Energy Gaps". Physical Review B. 44 (6): 2664–2672. Bibcode:1991PhRvB..44.2664W. doi:10.1103/physrevb.44.2664. PMID 9999836.
  15. ^ Moessner, R.; Sondhi, S. L. (2002). "Resonating Valence Bond Liquid Physics on the Triangular Lattice". Progress of Theoretical Physics Supplement. 145: 37–42. arXiv:cond-mat/0205029. Bibcode:2002PThPS.145...37M. doi:10.1143/PTPS.145.37. S2CID 119370249.
  16. ^ Kitaev, A.Yu.; Balents, Leon (2003). "Fault-tolerant quantum computation by anyons". Annals of Physics. 303 (1): 2–30. arXiv:quant-ph/9707021. Bibcode:2003AnPhy.303....2K. doi:10.1016/S0003-4916(02)00018-0. S2CID 119087885.
  17. ^ Knolle, Johannes; Moessner, Roderich (2019). "A field guide to spin liquids". Annual Review of Condensed Matter Physics. 10: 451–472. arXiv:1804.02037. Bibcode:2019ARCMP..10..451K. doi:10.1146/annurev-conmatphys-031218-013401. S2CID 85529148.
  18. ^ a b c Norman, M.R. (2016). "Herbertsmithite and the Search for the Quantum Spin Liquid". Reviews of Modern Physics. 88 (4): 041002. arXiv:1710.02991. doi:10.1103/RevModPhys.88.041002. S2CID 118727125.
  19. ^ Phys. 개정판 116, 107203 (2016)
  20. ^ Nytko, Emily A.; Helton, Joel S.; Müller, Peter; Nocera, Daniel G. (2008). "A Structurally Perfect S = 1/2 Metal−Organic Hybrid Kagome Antiferromagnet". Journal of the American Chemical Society. 130 (10): 2922–2923. doi:10.1021/ja709991u. PMID 18275194.
  21. ^ Matan, K.; Ono, T.; Fukumoto, Y.; Sato, T. J.; et al. (2010). "Pinwheel valence-bond solid and triplet excitations in the two-dimensional deformed kagome lattice". Nature Physics. 6 (11): 865–869. arXiv:1007.3625. Bibcode:2010NatPh...6..865M. doi:10.1038/nphys1761. S2CID 118664640.
  22. ^ a b Y. Shimizu; K. Miyagawa; K. Kanoda; M. Maesato; et al. (2003). "Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice". Physical Review Letters. 91 (10): 107001. arXiv:cond-mat/0307483. Bibcode:2003PhRvL..91j7001S. doi:10.1103/PhysRevLett.91.107001. PMID 14525498. S2CID 4652670.
  23. ^ 문헌에서 J 값은 일반적으로 에너지 대신 온도 단위( B { J로 표시됩니다.
  24. ^ T. Ng & P. A. Lee (2007). "Power-Law Conductivity inside the Mott Gap: Application to κ-(BEDT-TTF)2Cu2(CN)3". Physical Review Letters. 99 (15): 156402. arXiv:0706.0050. Bibcode:2007PhRvL..99o6402N. doi:10.1103/PhysRevLett.99.156402. PMID 17995193. S2CID 45188091.
  25. ^ Coldea, R.; Tennant, D.A.; Tsvelik, A.M.; Tylczynski, Z. (12 Feb 2001). "Experimental realization of a 2D fractional quantum spin liquid". Physical Review Letters. 86 (7): 1335–1338. arXiv:cond-mat/0007172. Bibcode:2001PhRvL..86.1335C. doi:10.1103/PhysRevLett.86.1335. PMID 11178077. S2CID 39524266. 프리프린트는 2000년에 업로드 된 것에 주의해 주세요.
  26. ^ Kohno, Masanori; Starkh, Oleg A; Balents, Leon (2007). "Spinons and triplons in spatially anisotropic frustrated antiferromagnets". Nature Physics. 3 (11): 790. arXiv:0706.2012. Bibcode:2007NatPh...3..790K. doi:10.1038/nphys749. S2CID 28004603.
  27. ^ Pratt, F. L.; Baker, P. J.; Blundell, S. J.; Lancaster, T.; et al. (2011). "Magnetic and non-magnetic phases of a quantum spin liquid". Nature. 471 (7340): 612–616. Bibcode:2011Natur.471..612P. doi:10.1038/nature09910. PMID 21455176. S2CID 4430673.
  28. ^ Elser, Veit (1989). "Nuclear antiferromagnetism in a registered 3He solid". Physical Review Letters. 62 (20): 2405–2408. Bibcode:1989PhRvL..62.2405E. doi:10.1103/PhysRevLett.62.2405. PMID 10039977.
  29. ^ Yan, Simeng and Huse, David A and White, Steven R (2011). "Spin-liquid ground state of the S=1/2 kagome Heisenberg antiferromagnet". Science. 332 (6034): 1173–1176. arXiv:1011.6114. Bibcode:2011Sci...332.1173Y. doi:10.1126/science.1201080. PMID 21527676. S2CID 34864628.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
  30. ^ Shores, Matthew P; Nytko, Emily A; Bartlett, Bart M; Nocera, Daniel G (2005). "A Structurally Perfect S=1/2 Kagome Antigerromagnet". Journal of the American Chemical Society. 127 (39): 13462–13463. doi:10.1021/ja053891p. PMID 16190686.
  31. ^ Helton, J. S.; et al. (2007). "Spin Dynamics of the Spin-1/2 Kagome Lattice Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters. 98 (10): 107204. arXiv:cond-mat/0610539. Bibcode:2007PhRvL..98j7204H. doi:10.1103/PhysRevLett.98.107204. PMID 17358563. S2CID 23174611.
  32. ^ Olariu, A; et al. (2008). "17O NMR Study of the Intrinsic Magnetic Susceptibility and Spin Dynamics of the Quantum Kagome Antiferromagnet ZnCu3(OH)6Cl2". Physical Review Letters. 100 (9): 087202. arXiv:0711.2459. Bibcode:2008PhRvL.100h7202O. doi:10.1103/PhysRevLett.100.087202. PMID 18352658. S2CID 2682652.
  33. ^ de Vries, M. A.; Stewart, J. R.; Deen, P. P.; Piatek, J. O.; Nilsen, G. J.; Ronnow, H. M.; Harrison, A. (2009). "Scale-free antiferromagnetic fluctuations in the S=1/2 kagome antiferromagnet herbertsmithite". Physical Review Letters. 103 (23): 237201. arXiv:0902.3194. Bibcode:2009PhRvL.103w7201D. doi:10.1103/PhysRevLett.103.237201. ISSN 0031-9007. PMID 20366167. S2CID 2540295.
  34. ^ Mendels, Philippe; Bert, Fabrice (2010). "Quantum kagome antiferromagnet: ZnCu3(OH)6Cl2". Journal of the Physical Society of Japan. 79 (1): 011001. arXiv:1001.0801. Bibcode:2010JPSJ...79a1001M. doi:10.1143/JPSJ.79.011001. S2CID 118545779.
  35. ^ Han, TH and Helton, JS and Chu, S and Prodi, Andrea and Singh, DK and Mazzoli, Claudio and M{\"u}ller, P and Nocera, DG and Lee, Young S (2011). "Synthesis and characterization of single crystals of the spin-1/2 kagome-lattice antiferromagnets Znx Cu4-x(OH)6Cl2" (PDF). Physical Review B. 83 (10): 100402. doi:10.1103/PhysRevB.83.100402.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
  36. ^ Han, Tian-Heng and Helton, Joel S and Chu, Shaoyan and Nocera, Daniel G and Rodriguez-Rivera, Jose A and Broholm, Collin and Lee, Young S (2012). "Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet". Nature. 492 (7429): 406–410. arXiv:1307.5047. Bibcode:2012Natur.492..406H. doi:10.1038/nature11659. PMID 23257883. S2CID 4344923.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
  37. ^ Fu, Mingxuan; Imai, Takashi; Lee, Young S (2015). "Evidence for a gapped spin-liquid ground state in a kagome Heisenberg antiferromagnet". Science. 350 (6261): 655–658. arXiv:1511.02174. Bibcode:2015Sci...350..655F. doi:10.1126/science.aab2120. PMID 26542565. S2CID 22287797.
  38. ^ Han, Tian-Heng and Norman, MR and Wen, J-J and Rodriguez-Rivera, Jose A and Helton, Joel S and Broholm, Collin and Lee, Young S (2016). "Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite". Physical Review B. 94 (6): 060409. arXiv:1512.06807. Bibcode:2016PhRvB..94f0409H. doi:10.1103/PhysRevB.94.060409. S2CID 115149342.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
  39. ^ a b c Amusia, M.; Popov, K.; Shaginyan, V.; Stephanovich, V. (2014). Theory of Heavy-Fermion Compounds - Theory of Strongly Correlated Fermi-Systems. Springer Series in Solid-State Sciences. Vol. 182. Springer. doi:10.1007/978-3-319-10825-4. ISBN 978-3-319-10825-4.
  40. ^ Wen, Jinsheng; Yu, Shun-Li; Li, Shiyan; Yu, Weiqiang; Li, Jian-Xin (12 September 2019). "Experimental identification of quantum spin liquids". NPJ Quantum Materials. 4 (1): 12. arXiv:1904.04435. Bibcode:2019npjQM...4...12W. doi:10.1038/s41535-019-0151-6. ISSN 2397-4648. S2CID 104292206.
  41. ^ a b Helton, J. S.; et al. (1472). "Dynamic Scaling in the Susceptibility of the Spin-1/2 Kagome Lattice Antiferromagnet Herbertsmithite". Physical Review Letters. 104 (14): 147201. arXiv:1002.1091. Bibcode:2010PhRvL.104n7201H. doi:10.1103/PhysRevLett.104.147201. PMID 20481955. S2CID 10718733.
  42. ^ de Vries, M. A.; et al. (2008). "The magnetic ground state of an experimental S=1/2 kagomé antiferromagnet". Physical Review Letters. 100 (15): 157205. arXiv:0705.0654. Bibcode:2008PhRvL.100o7205D. doi:10.1103/PhysRevLett.100.157205. PMID 18518149.
  43. ^ a b c Shaginyan, V. R.; Amusia, M. Ya.; Msezane, A. Z.; Popov, K. G. (2010). "Scaling Behavior of Heavy Fermion Metals". Physics Reports. 492 (2–3): 31. arXiv:1006.2658. Bibcode:2010PhR...492...31S. CiteSeerX 10.1.1.749.3376. doi:10.1016/j.physrep.2010.03.001. S2CID 119235769.
  44. ^ Pozo, Guillermo; de la Presa, Patricia; Prato, Rafael; Morales, Irene; Marin, Pilar; Fransaer, Jan; Dominguez-Benetton, Xochitl (2020). "Spin transition nanoparticles made electrochemically". Nanoscale. 12 (9): 5412–5421. doi:10.1039/C9NR09884D. PMID 32080699.
  45. ^ Gegenwart, P.; et al. (2006). "High-field phase diagram of the heavy-fermion metal YbRh2Si2". New Journal of Physics. 8 (9): 171. Bibcode:2006NJPh....8..171G. doi:10.1088/1367-2630/8/9/171.
  46. ^ a b Shaginyan, V. R.; Msezane, A.; Popov, K. (2011). "Thermodynamic Properties of Kagome Lattice in ZnCu3(OH)6Cl2 Herbertsmithite". Physical Review B. 84 (6): 060401. arXiv:1103.2353. Bibcode:2011PhRvB..84f0401S. doi:10.1103/PhysRevB.84.060401. S2CID 118651738.
  47. ^ 잉란, 마이클 에르멜, 패트릭 ALee, Xiao-Gang Wen, (2006), "가고메 격자의 Spin-1/2 Heisenberg 모델의 파동함수 투영 연구", 。
  48. ^ "New state of matter detected in a two-dimensional material". Retrieved 5 April 2016.
  49. ^ Banerjee, A.; Bridges, C. A.; Yan, J.-Q.; Aczel, A. A.; Li, L.; Stone, M. B.; Granroth, G. E.; Lumsden, M. D.; Yiu, Y.; Knolle, J.; Bhattacharjee, S.; Kovrizhin, D. L.; Moessner, R.; Tennant, D. A.; Mandrus, D. G.; Nagler, S. E. (2016). "Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet". Nature Materials. 15 (7): 733–740. arXiv:1504.08037. Bibcode:2016NatMa..15..733B. doi:10.1038/nmat4604. PMID 27043779. S2CID 3406627.
  50. ^ a b Shaginyan, V. R.; et al. (2012). "Identification of Strongly Correlated Spin Liquid in Herbertsmithite". EPL. 97 (5): 56001. arXiv:1111.0179. Bibcode:2012EL.....9756001S. doi:10.1209/0295-5075/97/56001. S2CID 119288349.
  51. ^ Wood, Charlie (2021-12-02). "Realizing topologically ordered states on a quantum processor". Science. 374 (6572): 1237–1241. arXiv:2104.01180. Bibcode:2021Sci...374.1237S. doi:10.1126/science.abi8378. PMID 34855491. S2CID 233025160. Retrieved 2021-12-04.{{cite journal}}: CS1 maint :url-status (링크)
  52. ^ Wood, Charlie (2021-12-02). "Quantum Simulators Create a Totally New Phase of Matter". Quanta Magazine. Retrieved 2022-03-11.
  53. ^ Satzinger, K. J.; Liu, Y.-J; Smith, A.; Knapp, C.; Newman, M.; Jones, C.; Chen, Z.; Quintana, C.; Mi, X.; Dunsworth, A.; Gidney, C. (2021-12-03). "Realizing topologically ordered states on a quantum processor". Science. 374 (6572): 1237–1241. arXiv:2104.01180. Bibcode:2021Sci...374.1237S. doi:10.1126/science.abi8378. PMID 34855491. S2CID 233025160.
  54. ^ Verresen, Ruben; Lukin, Mikhail D.; Vishwanath, Ashvin (2021-07-08). "Prediction of Toric Code Topological Order from Rydberg Blockade". Physical Review X. 11 (3): 031005. arXiv:2011.12310. Bibcode:2021PhRvX..11c1005V. doi:10.1103/PhysRevX.11.031005. S2CID 227162637.
  55. ^ Semeghini, G.; Levine, H.; Keesling, A.; Ebadi, S.; Wang, T. T.; Bluvstein, D.; Verresen, R.; Pichler, H.; Kalinowski, M.; Samajdar, R.; Omran, A. (2021-12-03). "Probing topological spin liquids on a programmable quantum simulator". Science. 374 (6572): 1242–1247. arXiv:2104.04119. Bibcode:2021Sci...374.1242S. doi:10.1126/science.abi8794. PMID 34855494. S2CID 233204440.
  56. ^ Aguilar, Mario (December 20, 2012). "This Weird Crystal Demonstrates a New Magnetic Behavior That Works Like Magic". Gizmodo. Retrieved 24 December 2012.
  57. ^ Fendley, Paul. "Topological Quantum Computation from non-abelian anyons" (PDF). University of Virginia. Archived from the original (PDF) on 2013-07-28. Retrieved 24 December 2012.
  58. ^ Chandler, David (December 20, 2012). "New kind of magnetism discovered: Experiments demonstrate 'quantum spin liquid'". Phys.org. Retrieved 24 December 2012.