오일러 특성

수학에서, 그리고 더 구체적으로 대수 위상과 다면 결합체에서 오일러 특성(또는 오일러 숫자, 또는 오일러-핀카레 특성)은 위상학적 불변성으로, 위상 공간의 형태나 구조를 구부리는 방법에 관계없이 설명하는 숫자다. 일반적으로 $\chi {\displaystyle }$ ${\displaystyle \chi}($그리스어 소문자 chi)로 표시된다.

오일러 특성은 원래 다면체에 대해 정의되었으며 플라토닉 고형물의 분류를 포함한 그에 대한 다양한 이론들을 증명하는데 사용되었다. 그것은 1537년 프란체스코 마우로리코가 출판하지 않은 원고에서 플라토닉 고형분에 대해 언급되었다.^[1] 개념명이 붙여진 레온하르트 오일러는 보다 일반적으로 볼록한 다면체용으로 도입했지만 불변체라는 것을 엄격하게 입증하지는 못했다. 현대 수학에서 오일러 특성은 호몰로지, 더 추상적으로 호몰로지 대수학에서 발생한다.

폴리헤드라

오일러 특성 $\chi {\displaystyle }$ ${\displaystyle \chi}$은 다면체의 표면에 대해 공식에 따라 분류적으로 정의되었다$$.

$\displaystyle \chi =V-E+F}$

여기서 V, E, F는 각각 주어진 다면체의 정점(코너), 가장자리 및 면의 수입니다. 모든 볼록 다면체의 표면은 오일러 특성을 가지고 있다.

$V-E+F=2 디스플레이 스타일 V-E+F=2).}$

1758년 레온하르트 오일러가 말한 이 방정식은 오일러의 다면체 공식으로 알려져 있다.^[2][3] 구의 오일러 특성(즉, = = 2)에 해당하며 구면 다면체에도 동일하게 적용한다. 모든 플라토닉 다면체의 공식은 아래와 같다.

이름	이미지	정점 V	가장자리 E	얼굴 F	오일러 특성: V − E + F
사면체		4	6	4	2
육면체 또는 정육면체		8	12	6	2
팔면체		6	12	8	2
도데카헤드론		20	30	12	2
이코사헤드론		12	30	20	2

비콘벡스 다면체의 표면은 다양한 오일러 특성을 가질 수 있다.

이름	이미지	정점 V	가장자리 E	얼굴 F	오일러 특성: V − E + F
테트라헤미헥사헤드론		6	12	7	1
옥타헤미오크타헤드론		12	24	12	0
큐보헤미오크타헤드론		12	24	10	−2
소절개도면체		12	30	12	−6
그레이트 스틸 도데카헤드론		20	30	12	2

일반 폴리헤드라의 경우, 아서 케일리는 밀도 D, 정점 수치 밀도_v d, 얼굴 ${\displaystyle {밀도}_{}}$ d f$${\$displaystyle d_{$f} :$$을러 공식의 변형된 형태를 도출했다.

${\displaystyle d_{v}V-E+d_{f}}F=2D.}$

이 버전은 볼록한 폴리헤드라(밀도가 모두 1인 곳)와 비콘벡스 케플러-푸인소트 폴리헤드라 모두를 보유한다.

투사성 다면체는 모두 실제 투사면과 같이 오일러 특성 1을 가지고 있는 반면, 토로이드성 다면체의 표면은 모두 오일러 특성 0을 가지고 있다.

평면 그래프

오일러 특성은 다면 표면과 ${\displaystyle \mathrm{동일}}$한 $V{\displaystyle }$- ${\displaystyle E}$+ F ${\displaystyle V-E+F}$ 공식으로$$ 연결된 평면 그래프에 대해 정의할 수 있으며, 여기서 F는 외부 표면을 포함한 그래프에서 면의 수입니다.

모든 평면 연결 그래프 G의 오일러 특성은 2이다. 이는 나무를 베이스 케이스로 시작해 G가 결정한 얼굴 수를 유도하면 쉽게 증명된다. For trees, ${\displaystyle E=V-1}$ and ${\displaystyle F=1}$. If G has C components (disconnected graphs), the same argument by induction on F shows that ${\displaystyle V-E+F-C=1}$. One of the few graph theory papers of Cauchy also proves this result.

입체 투영을 통해 평면은 2-sphere에 매핑되며, 이는 연결된 그래프가 오일러 특성 2를 갖는 구의 폴리곤 분해에 매핑된다. 이 관점은 아래에 제시된 오일러의 공식에 대한 코치의 증거에 내포되어 있다.

오일러의 공식 증명

오일러의 공식에는 많은 증거가 있다. 하나는 1811년 카우치(Cauchy)가 준 것으로 다음과 같다. 그것은 모든 볼록한 다면체에 적용되며, 보다 일반적으로 경계선이 구와 동일하고 얼굴이 원반과 동일한 다면체에 적용된다.

다면 표면의 한 면을 제거한다. 누락된 면의 가장자리를 서로 멀리 당겨서 나머지 부분을 모두 점과 곡선의 평면 그래프로 변형시켜 입방체의 특수 사례에 대한 세 개의 그래프 중 첫 번째 그래프에서 도해한 바와 같이, 누락된 면의 둘레가 외부로 배치되도록 한다. (다면체 표면이 처음에 구에 동형체라는 가정은 이것을 가능하게 한다.) 이러한 변형 이후, 보통 얼굴들은 일반적으로 더 이상 규칙적이지 않다. 정점과 가장자리 수는 그대로 유지되었으나 면수는 1로 줄어들었다. 따라서 다면체에 대한 오일러의 공식을 증명하면 이 변형된 평면 객체에 대해 V - E + F =1을 증명하는 것으로 감소한다.

세 면 이상의 면이 있는 경우 대각선, 즉 아직 연결되지 않은 두 꼭지점을 연결하는 면 사이로 곡선을 그린다. 이것은 하나의 가장자리와 하나의 면을 추가하며 정점의 수를 변경하지 않기 때문에 V - E + F의 양을 변경하지 않는다(모든 면이 디스크라는 가정은 요르단 곡선 정리를 통해 이 연산이 면 수를 1씩 증가시킨다는 것을 보여주기 위해 여기에 필요하다). 모든 면이 삼각형이 될 때까지 이 방법으로 가장자리를 계속 추가하십시오.

외부 경계가 항상 단순한 사이클이라는 불변성을 유지하면서 다음 두 가지 변환 중 하나를 반복적으로 적용하십시오.

1. 두 번째 그래프에 표시된 것처럼 외부와 인접한 하나의 가장자리만 있는 삼각형을 제거하십시오. 이것은 가장자리와 면의 수를 각각 하나씩 감소시키고 정점의 수를 변경하지 않기 때문에 V - E + F를 보존한다.
2. 세 번째 그래프에 표시된 것처럼 네트워크 외부가 공유하는 두 모서리가 있는 삼각형을 제거하십시오. 각 삼각형 제거는 정점, 두 개의 가장자리 및 한 면을 제거하므로 V - E + F를 보존한다.

이러한 변환은 결국 평면 그래프를 하나의 삼각형으로 감소시킨다.(단순 주기 불변량 없이 삼각형을 제거하면 나머지 삼각형이 분리되어 인수의 나머지가 무효화될 수 있다. 유효한 제거 명령은 포격의 기본적인 예)

이 시점에서 단독 삼각형은 V = 3, E = 3, F = 1을 가지므로 V - E + F = 1을 가진다. 위의 두 변환 단계가 각각 이 양을 보존하였으므로, 변형된 평면 객체에 대해 V - E + F = 1을 보여줌으로써 다면체에 대해 V - E + F = 2를 보여주었다. 이것이 정리를 증명한다.

추가 증거는 데이비드 엡스타인의 오일러 공식 20개 증명서를 참조하십시오.^[4] 임레 라카토스의 프루프 및 리퍼테이션에서 그 결함과 한계를 포함한 복수의 프루프가 예시로 사용된다.^[5]

위상학적 정의

위에서 논의한 다면 표면은 현대어로 2차원 유한 CW 복합체다. (삼각형 면만 사용할 경우 2차원 유한 단순화 콤플렉스) 일반적으로 유한 CW 복합체의 경우 오일러 특성은 교대로 정의할 수 있다.

${\displaystyle \chi =k_{0}-k_{1}+k_{2}-k_{3}+\cdots ,}$

여기서 k는_n 복합체에서 차원 n의 셀 수를 나타낸다.

마찬가지로, 단순 복합체의 경우 오일러 특성은 교대 합과 같다.

${\displaystyle \chi =k_{0}-k_{1}+k_{2}-k_{3}+\cdots ,}$

여기서 k는_n 단지 내 n-148x의 수를 나타낸다.

베티 번호 대안

보다 일반적으로는, 어떤 위상학적 공간에 대해서도, 우리는 n번째 베티 숫자_n b를 n번째 단수적 호몰로지 그룹의 등급으로 정의할 수 있다. 오일러 특성은 교대 합으로 정의할 수 있다.

${\displaystyle \chi =b_{0}-b_{1}+b_{2}-b_{3}+\cdots .}$

베티 숫자가 모두 유한하고 특정 지수 n을 넘어 0이면₀ 이 수량이 잘 정의된다. 단순화 단지의 경우, 이는 이전 단락과 동일한 정의는 아니지만, 호몰로지 계산을 통해 두 정의가 $\chi {\displaystyle }$ ${\displaystyle \chi$에 대해 동일한 값을 제공할 것이라는 것을 알 수 있다.

특성.

오일러 특성은 위상학적 공간에서 많은 기본적인 조작과 관련하여 다음과 같이 잘 동작한다.

호모토피 불협화음

호몰로지(homology)는 위상학적 불변성이며, 더욱이 호모토피 불변성은 다음과 같다. 호모토피와 동등한 두 개의 위상학적 공간은 이형동성 동질학 그룹을 가지고 있다. 이어 오일러 특성도 호모토피 불변제라고 한다.

예를 들어, 모든 계약 가능한 공간(즉, 한 점에 해당하는 하나의 호모토피)은 사소한 호몰로지(homotology)를 가지고 있는데, 이는 0번째 베티 번호는 1이고 나머지 호모토피는 0이라는 것을 의미한다. 따라서 오일러의 특징은 1이다. 이 사례에는 유클리드 공간 ${\displaystyle {}^{}}$ ${\$과(와) 모든$$ 유클리드 공간의 고체 단위 공(-1차원 간격, 2차원 디스크, 3차원 공 등)이 포함된다.

또 다른 예로, 어떤 볼록한 다면체는 3차원 공과 동형이기 때문에 표면은 2차원 구체와 동형(헨스 호모토피 등가)으로 오일러 특성 2를 가지고 있다. 이것은 볼록 폴리에드라가 오일러 특성 2를 가지는 이유를 설명한다.

포함-제외원칙

M과 N이 두 개의 위상학적 공간인 경우, 호몰로지(homology)는 이음매 결합 하에서 첨가되기 때문에 이음매 결합의 오일러 특성은 오일러 특성의 합이다.

$\displaystyle \chi(M\sqcup N)=\chi(M)+\chi(N)}$

보다 일반적으로, M과 N이 더 큰 공간 X의 하위 공간이라면, 이들의 결합과 교차점 또한 그렇다. 일부의 경우 오일러 특성은 포함-제외 원칙의 한 버전을 준수한다.

$\displaystyle \chi(M\cup N)=\chi(M)+\chi(N)-\chi(M\cap N)=\chi.}$

이는 다음과 같은 경우에 해당된다.

• 만약 M과 N이 흥분하는 부부라면 특히 노조 내부의 M과 N의 내부가 여전히 노조를 뒤덮고 있다면 말이다.^[6]
• X가 국소적으로 콤팩트한 공간이고 컴팩트한 지지대로 오일러 특성을 사용하는 경우 M이나 N에 대한 가정은 필요 없다.
• X가 층층이 균일한 층층 공간인 경우, M과 N이 층층 조합인 경우 포함-배제 원칙이 유지된다. 이것은 특히 M과 N이 복잡한 대수적 변종의 하위 변수인 경우에 적용된다.^[7]

일반적으로 포함-제외 원칙은 거짓이다. X를 실제 라인으로, M은 1점으로, N은 M의 보완으로 구성되는 서브셋을 취함으로써 counterexample이 주어진다.

연결합계

연결된 두 개의 닫힌 n-manifolds $M{\displaystyle }$, ${\displaystyle N}$ ${\displaystyle M,$${\displaystyle N}$$}$의 경우 연결된 sum 작업을 통해$$ 새 연결된 매니폴드 $M{\displaystyle \mathrm{}}$# N ${\displaystyle M\#N}$을(를) 얻을 수 있다. 오일러 특성은 공식에 의해 연관된다.

$\displaystyle \chi(M\#N)=\chi(M)+\chi(N)-\chi(S^{n}).}$

상품 속성

또한, 제품 공간 M × N의 오일러 특성은

$\displaystyle \chi(M\time N)=\chi(M)\cdot \chi(N).}$

이러한 덧셈과 곱셈 속성도 세트의 카디널리티에 의해 향유된다. 이러한 방식으로 오일러 특성은 카디널리티의 일반화로 볼 수 있다. [1]을 참조하십시오.

덮개 공간

마찬가지로 K-시트 피복 $공간{\displaystyle \stackrel{}{}}$ M${\displaystyle }$~ →${\displaystyle M}$ , ${\displaystyle${\$tilde{M}\to$ M$}$의 경우

${\displaystyle \chi({\tilde{M})=k\cdot \chi(M).}$

보다 일반적으로 래미티드 커버 공간의 경우, 커버의 오일러 특성은 래미션 포인트에 대한 보정 계수를 사용하여 위에서부터 계산할 수 있으며, 이는 리만–을 산출한다.허위츠 공식.

진동 특성

제품 속성은 특정 조건의 섬유에 대해 훨씬 더 일반적으로 유지된다.

$p{\displaystyle }$: ${\displaystyle E}$→ ${\displaystyle B}$ ${\displaystyle p\colon E\to B}$이(가) 베이스 B 경로가 연결된 F섬유로 진동이 되고$$, 진동이 필드 K에 걸쳐 방향을 잡을 수 있는 경우, 필드 K에 계수가 있는 오일러 특성은 다음과 같은 제품 특성을 만족시킨다.^[9]

$\displaystyle \chi(E)=\chi(F)\cdot \chi(B).}$

여기에는 제품 공간과 덮개 공간이 특수 사례로 포함되며, 진동 동질학에 대한 Serre 스펙트럼 시퀀스로 증명될 수 있다.

For fiber bundles, this can also be understood in terms of a transfer map ${\displaystyle \tau \colon H_{*}(B)\to H_{*}(E)}$ – note that this is a lifting and goes "the wrong way" – whose composition with the projection map ${\displaystyle p_{*}\colon H_{*}(E)\to H$$_{*}(B)}$은(^[10]는) 섬유의 오일러 클래스에 의한 곱이다.

$\displaystyle p_{*}\circu \tau =\chi(F)\cdot 1.}$

예

표면

오일러 특성은 표면의 폴리곤화(즉, CW 복합체로서의 설명)를 찾아 위의 정의를 사용하여 일반 표면에 대해 쉽게 계산할 수 있다.

이름	이미지	χ
간격		01
원		00
디스크		01
구		02
토러스 (제품 두 개의 원)		00
더블 토러스		−2
트리플 토러스		−4
리얼 프로젝티브 평면을 이루다		01
뫼비우스 스트립		00
클라인 병		00
두 개의 구 (연결되지 않음) (해체조합 두 개의 구 중에서)		2 + 2 = 4
삼구 (연결되지 않음) (해체조합 세 개의 구 중에서)		2 + 2 + 2 = 6
$[\displaystylen]$ 구들$$ (연결되지 않음) (n 구체의 공동 결합 )	. . .	2 + … + 2 = 2n

축구공

각 꼭지점에서 세 개의 조각이 만나는 오각형과 육각형의 조각을 꿰매 축구공을 만드는 것이 일반적이다(예: 아디다스 텔스타 참조). P 펜타곤과 H 육각형을 사용할 경우 F = P + H 면, V = (5 P + 6 H) / 3 정점, E = (5 P + 6 H) / 2 엣지가 있다. 오일러 특성은 다음과 같다.

${\displaystyle V-E+F={\frac {5P+6H}{3}-{\frac {5P+6H}{2}}+P+H={\frac {P}{6}}.}$

구는 오일러 특성 2를 가지고 있기 때문에, 그 P = 12를 따른다. 즉, 이런 식으로 만들어진 축구공은 항상 12개의 펜타곤을 가지고 있다. 원칙적으로 육각의 수는 제약이 없다. 이 결과는 풀레네와 골드버그 폴리헤드라에 적용된다.

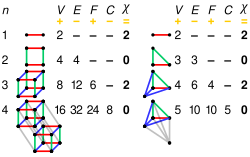
임의 치수

일반 다면체의 4차원 유사점 6개의 오일러 특성

정규 4칸짜리	V (k0)	E (k1)	F (k2)	C (k3)	${\displaystyle \chi }$ ${\displaystyle \chi}$ $$= V - E + F − C
5세포	5	10	10	5	0
8셀	16	32	24	8	0
16 셀	8	24	32	16	0
24셀	24	96	96	24	0
120 셀	600	1200	720	120	0
600셀	120	720	1200	600	0

n차원 구에는 다음과 같은 단수 동음이의 집단들이 있다.

${\displaystyle H_{k}(S^{n})={\begin{case}\mathb {Z} &k=0,n\\\{0\}>{\text{otherwise,}}}}}}}}}}$

따라서 치수 0과 n에 베티 번호 1이 있으며, 다른 모든 베티 번호는 0이다. 오일러 특성은 1 + (-1) ⁿ- 즉, 0 또는 2이다.

n차원 실제 투영 공간은 n-sphere의 반투명 지도에 의한 몫이다. 따라서 오일러 특성은 0 또는 1의 해당 구체의 정확히 절반이다.

n차원 토러스(torus)는 n개의 원들의 생산 공간이다. 오일러 특성은 제품 특성에 의해 0이다. 보다 일반적으로 콤팩트한 Lie 그룹을 포함하여 모든 콤팩트한 병렬처리 가능한 다지관은 오일러 특성 0을 가진다.^[11]

닫힌 홀수차원 다지관의 오일러 특성도 0이다.^[12] 오리엔테이션 가능한 예에 대한 사례는 푸앵카레 이중성의 상각이다. 이 특성은 층층이 모두 홀수 치수를 갖는 모든 컴팩트한 층층 공간에 더 일반적으로 적용된다. 또한 2:1 방향성 이중 커버를 통해 닫힌 홀수차원 비방향성 다지관에도 적용된다.

다른 불변제와의 관계

밀폐된 방향성 표면의 오일러 특성은 속 g(표면의 연결된 총분해에서 토리의 수; 직관적으로 "핸들"의 수)에서 다음과 같이 계산할 수 있다.

$\displaystyle \chi =2-2g.}$

밀폐된 비방향성 표면의 오일러 특성은 비방향성 속 k(표면의 연결된 총분해에서 실제 투영면의 수)에서 다음과 같이 계산할 수 있다.

$\displaystyle \chi =2-k.}$

닫힌 매끄러운 다지관의 경우 오일러 특성은 오일러 번호, 즉 다지관의 기본 등급에서 평가된 접선다발의 오일러 등급과 일치한다. 오일러 클래스는 벡터 번들의 다른 모든 특성 클래스와 관련된다.

폐쇄형 리만 다지관의 경우 곡률을 통합하여 오일러 특성을 찾을 수도 있다. 2차원 사례의 경우 가우스-보넷 정리, 일반 사례의 경우 일반화된 가우스-보넷 정리를 참조한다.

가우스-보넷 정리의 이산형 아날로그는 데카르트의 정리로서, 전체 원형으로 측정한 다면체의 "총결함"이 다면체의 오일러 특성; 결점(지오메트리)을 참조한다.

하드와이거의 정리는 오일러 특성을 "도 0의 동종"인 R의ⁿ 콤팩트 볼록 세트의 유한 조합에 정의된 고유(스칼라 곱셈까지) 변환불변, 정밀하게 첨가, 불필요한 음의 집합함수로 특징짓는다.

일반화

모든 결합 세포 복합체에 대해, 이 교대 합이 유한할 경우, 오일러 특성을 0셀 수, 1셀 수, 2셀 수 등을 뺀 값으로 정의한다. 특히 유한 집합의 오일러 특성은 단순히 카디널리티일 뿐이고, 그래프의 오일러 특성은 정점수에서 가장자리 수를 뺀 것이다.^[13]

보다 일반적으로는 어떤 체인단지의 오일러 특성을 이 모든 등급이 유한하다고 가정할 때 체인단지의 호몰로지 집단의 등급의 교대 합이라고 정의할 수 있다.^[14]

대수 기하학에 사용되는 오일러 특성의 버전은 다음과 같다. 적절한 체계 X에 대한$$ 일관성 있는 sheaf $F{\displaystyle \mathcal{}}$ ${\$에 대해서는 오일러 특성을 다음과 같이 정의한다.

${\displaystyle \chi({\mathcal{F}}}=\sum _{i}(1)^{i}h^{i}(X, {\mathcal {F}),}$

여기서 h ${\displaystyle i^{}}$(${\displaystyle X\mathcal{}}$, F${\displaystyle }$) ${\displaystyle h^{i}(X,{\mathcal {F})$는 $F{\displaystyle \mathcal{}}$ ${\$의 i-thheaf 코호몰로지 그룹의 치수$.$ 이 경우 치수는 모두 Grotendieck의 정밀도 정리에 의해 유한하다. 체인 콤플렉스의 오일러 특성의 한 예로서, 체인 콤플렉스는 Acyclic sheave에 의한$$ $F{\displaystyle \mathcal{}}$ ${\$의 유한 분해능이다.

다지관의 오일러 특성의 또 다른 일반화는 오비폴드에서 온다(오비폴드의 오일러 특성 참조). 모든 다지관에는 정수 오일러 특성이 있지만, 오비폴드에는 소수 오일러 특성이 있을 수 있다. 예를 들어, 눈물방울 오비폴드는 오일러 특성 1 + 1/p를 가지고 있는데, 여기서 p는 원뿔 각 2π / p에 해당하는 소수다.

경계 유한양성의 감소된 호몰로지 오일러 특성의 개념은 조합학에서 중요한 또 다른 일반화다. 포셋이 가장 작고 가장 큰 요소를 가진 경우 포셋은 "경계"가 된다. 포셋을 0과 1이라고 부른다. 그러한 포지셋의 오일러 특성은 정수 μ(0,1)로 정의되며, 여기서 μ는 해당 포지셋의 발생 대수에서 뫼비우스 함수다.

이는 위에서 언급한 그래프, 오비폴드 및 포셋의 오일러 특성과 호환되는 개념인 특정 유한 범주에 대한 Q-값 오일러 특성을 정의함으로써 더욱 일반화될 수 있다. 이 설정에서 유한군 또는 모노이드 G의 오일러 특성은 1/ G이고, 유한군 G의 오일러 특성은 1_i/ G의 합으로, 여기서 그룹오이드의 연결된 각 구성 요소에 대해 하나의 대표군 G를_i 선택했다.^[15]

참고 항목

• 오일러 미적분학
• 오일러급
• 레온하르트 오일러의 이름을 딴 주제 목록
• 균일한 다면체 목록

참조

메모들

참고 문헌 목록

• Richeson, David S.; 오일러의 보석: 다면체 공식과 위상의 탄생. 프린스턴 대학 출판부 2008.

추가 읽기

• Flegg, H. Graham; 도버 2001, 페이지 40.

외부 링크

• Weisstein, Eric W. "Euler characteristic". MathWorld.
• Weisstein, Eric W. "Polyhedral formula". MathWorld.
• Matveev, S.V. (2001) [1994], "Euler characteristic", Encyclopedia of Mathematics, EMS Press
• 구형 기하를 사용한 오일러의 공식 증명 애니메이션 버전.