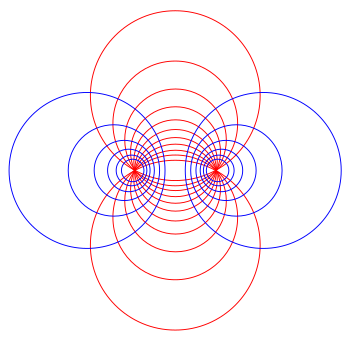
2차원 양극 좌표계를 두 포커스를 분리하는 축에 대해 회전하여 얻은 토로이드 좌표 그림. 초점은 수직 z축으로부터 1 거리에 위치한다. $xy$-plane 위에 놓여 있는 적색 구체의 부분은 30 = 30° 이소수면이고, 파란색 torus는 τ = 0.5 이소수면이며, 노란색 반평면은 φ = 60° 이소수면이다. 녹색 반평면은 x-z 검은색 점은 빨간색, 파란색 및 노란색 이소서페이스의 교차점, 대략적으로 카르테시안 좌표(0.996, -1.725, 1.911)에 위치한다. 토로이드 좌표 는 3차원 직교 좌표계 로, 2차원 양극 좌표계 를 그것의 두 초점을 분리하는 축을 중심으로 회전시킴으로써 생긴다. 따라서 양극 좌표 에 있는두 개 F displaystyle F_{ F F_{2}} x y {\displaystyle xy} 있는 {\displaystyle a} z {\displaystyle z} 초점 링은 참조 원이라고도 한다.
정의 토로이드 좌표의 가장 일반적인 {\ displaystyle (\sigma ,\tau ,\phi )} .
x = a 징징거리다 τ 코쉬 τ − cas σ cas ϕ {\displaystyle x=a\\\\frac {\sinh \tau }{\cosh \tau -\coses \coses \pi }} y = a 징징거리다 τ 코쉬 τ − cas σ 죄를 짓다 ϕ {\displaystyle y=a\\\\frac {\sinh \tau }{\cosh \tau -\coses \cosh \phi }}} z = a 죄를 짓다 σ 코쉬 τ − cas σ {\displaystyle z=a\\\\frac {\sin \sin \sigma }{\cosh \tau -\coses \cosma }}} s i g n σ s i g z {\displaystyle \mathrm sign}(\ })(\mathrm }=\mathrm {sign}(z}) 점 P displaystyle P} σ {\displaystyle \sigma } 1 P 2 {\ displaystyle F_{1} PF_{2 and {\displaystyle \tau} d 1 {\ displaystyle d_{1 d 2 {\ displaystyle d_{2 자연 로그 와 같다.
τ = ln d 1 d 2 . {\displaystyle \tau =\ln {\frac {d_{1}:{d_{2}}. } 좌표 범위는 - π σ ≤ displaystyle \pi <\sigma \leq \pi 0 0 {\displaystyle \tau \geq 0}, 0 ≤ 2 \. {\displaystyleq \pi i
좌표면 이 2차원 양극 좌표계 를 수직 축에 대해 회전시키면 위의 3차원 토로이드 좌표계가 생성된다. 수직축에 있는 원은 붉은 구가 되고, 수평축에 있는 원은 청색 토루스가 된다. 상수 σ {\displaystyle \sigma}
( x 2 + y 2 ) + ( z − a 요람을 달다 σ ) 2 = a 2 죄를 짓다 2 σ {\displaystyle \left(x^{2}+y^{2}\2}\right)+\좌(z-a\a\ma \sigma \right)^{2}={\frac{a^{2}}{\sin ^{2}\ma}}}}}}} 모든 것이 초점 고리를 통과하지만 동심원이 아니다. 상수 τ {\displaystyle \tau }
z 2 + ( x 2 + y 2 − a 나무늘보 τ ) 2 = a 2 징징거리다 2 τ {\displaystyle z^{2}+\left\sqrt {x^{2}+y^{2}}-a-\cot \tau \right)^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}}}}}} 초점 링을 둘러싸고 있는. 상수 σ {\displaystyle \sigma } 중심 {\displaystyle z} 상수 {\displaystyle \tau 토리 y {\displaysty xy}
역변환 ( σ τ ϕ {\displaystyle (\sigma ,\tau ,\phi )} x , y, z )에서 계산할 수 있다. 방위각 ϕ {\displaystyle \pi }
햇볕에 그을리다 ϕ = y x {\displaystyle \tan \phi ={\frac {y}{x}}}} P 지점의ρ {\displaystyle \rho }
ρ 2 = x 2 + y 2 = ( a 징징거리다 τ 코쉬 τ − cas σ ) 2 {\displaystyle \rho ^{2}=x^{2}+y^{2}=\왼쪽(a{\frac {\\sinh \tau }{\cosh \tau -}{\cos \cos \}{2}}: and {\displaystyle \phi }
d 1 2 = ( ρ + a ) 2 + z 2 {\displaystyle d_{1}^{2}=(\rho +a)^{2}+z^{2 }} d 2 2 = ( ρ − a ) 2 + z 2 {\displaystyle d_{2}^{2}^{2}=(\rho -a)^{2}+z^{2 }} 점 P 의 좌표 σ과 τ의 기하학적 해석. 일정한 방위각 ϕ {\displaystyle \phi } , 양극 좌표 와 동등하다. 각도 σ {\displaystyle \sigma } P 의 두 포커에 의해 형성되는τ {\displaystyle \tau } 상수 σ {\displaystyle \sigma } 와 display displaystyle } 좌표 τ {\displaystyle \tau } 자연 로그 와 같다
τ = ln d 1 d 2 {\displaystyle \tau =\ln {\frac {d_{1}:{d_{2}}: 반면 whereas {\ displaystyle \sigma} 코사인 법칙 에 따라 결정될 수 있는 포커스에 대한 광선 사이의 각도와 같다
cas σ = d 1 2 + d 2 2 − 4 a 2 2 d 1 d 2 . {\displaystyle \cos \sigma ={\frac {d_{1}^{2}+d_{2} }^{2}-4a^{2}}:{2d_{1}d_{2}}. } 아니면 그 간판을 포함해서
σ = s i g n ( z ) 아르코스 r 2 − a 2 ( r 2 − a 2 ) 2 + 4 a 2 z 2 {\displaystyle \mathrm {sign}(z)\arccos {\r^{2}-a^{2}}:{\sqrt{(r^{2}-a^{2})^{2}+4a^{2}}:} 여기서 r ρ 2 z 2 {\ displaystyle r={\sqrt {\rho^{2}+z^{2 }}}}
원통형 좌표와 토로이드 좌표 사이의 변환은 다음과 같이 복잡한 표기법으로 표현할 수 있다.
z + i ρ = i a 나무늘보 τ + i σ 2 , {\displaystyle z+i\rho \ =ia\cots {\frac {\tau +i\i\ma}{2}},} τ + i σ = ln z + i ( ρ + a ) z − i ( ρ − a ) . {\displaystyle \tau +i\i\ma \=\ln {\frac {z+i(\rho +a)}{z-i(\rho -a)}}. } 척도계수 토로이드 좌표 coordinates {\displaystyle \sigma } 와) display tau }
h σ = h τ = a 코쉬 τ − cas σ {\displaystyle h_{\buma }=h_{\\tau }={\frac {a}{\cosh \tau -\coses \ma}}}} 방위 척도 계수가 동일한 반면
h ϕ = a 징징거리다 τ 코쉬 τ − cas σ {\displaystyle h_{\phi }={\frac {a\sinh \tau }{\cosh \tau -\coses \ma}}}} 따라서 최소 볼륨 요소는 동일하다.
d V = a 3 징징거리다 τ ( 코쉬 τ − cas σ ) 3 d σ d τ d ϕ {\dplaystyle dV={\frac {a^{3}\sinh \tau \}{\\\cos \sigma \right)^{3}}\,d\tau \,d\tau \,d\pi }} 차등 연산자 라플라시아인은 에 의해 주어진다.
∇ 2 Φ = ( 코쉬 τ − cas σ ) 3 a 2 징징거리다 τ [ 징징거리다 τ ∂ ∂ σ ( 1 코쉬 τ − cas σ ∂ Φ ∂ σ ) + ∂ ∂ τ ( 징징거리다 τ 코쉬 τ − cas σ ∂ Φ ∂ τ ) + 1 징징거리다 τ ( 코쉬 τ − cas σ ) ∂ 2 Φ ∂ ϕ 2 ] {\displaystyle {\begin{aligned}\nabla ^{2}\Phi ={\frac {\left(\cosh \tau -\cos \sigma \right)^{3}}{a^{2}\sinh \tau }}&\left[\sinh \tau {\frac {\partial }{\partial \sigma }}\left({\frac {1}{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \sigma }}\right)\right. \\[8pt]&{}\nowled +\왼쪽. {\frac {\partial }{\partial \tau }}\left({\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \tau }}\right)+{\frac {1}{\sinh \tau \left(\cosh \tau -\cos \sigma \right)}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}\right]\end{aligned}}}
For a vector field n → ( τ , σ , ϕ ) = n τ ( τ , σ , ϕ ) e ^ τ + n σ ( τ , σ , ϕ ) e ^ σ + n ϕ ( τ , σ , ϕ ) e ^ ϕ {\displaystyle {\vec {n}}(\tau ,\sigma ,\phi )=n_{\tau }(\tau ,\sigma ,\phi ){\hat {e}}_{\tau }+n_{\sigma }(\tau ,\sigma ,\phi ){\hat {e}}_{\sigma }+n_{\phi }(\tau ,\sigma ,\phi ){\ hat {e}_{\phi }},
Δ n → ( τ , σ , ϕ ) = ∇ ( ∇ ⋅ n → ) − ∇ × ( ∇ × n → ) {\displaystyle \delta {n}(\tau ,\sigma ,\phi )=\nabla(\nabla \cdot {\\vec{n}}}-\nabla \times{\n})} = 1 a 2 e → τ { n τ ( − 징징거리다 4 τ + ( 코쉬 τ − cas σ ) 2 징징거리다 2 τ ) + n σ ( − 징징거리다 τ 죄를 짓다 σ ) + ∂ n τ ∂ τ ( ( 코쉬 τ − cas σ ) ( 1 − 코쉬 τ cas σ ) 징징거리다 τ ) + … {\displaystyle ={\frac {1}{a^{2}}}{\vec {e}}_{\tau }\left\{n_{\tau }\left(-{\frac {\sinh ^{4}\tau +(\cosh \tau -\cos \sigma )^{2}}{\sinh ^{2}\tau }}\right)+n_{\sigma }(-\sinh \tau \sin \sigma )+{\frac {\partial n_{\tau }}{\partial \tau }}\left({\frac {(\cosh \tau -\cos \sigma )(1-\cosh \tau \cos \sigma )}{\sinh \tau }}\right)+\ldots \right. }
+ ∂ n τ ∂ σ ( − ( 코쉬 τ − cas σ ) 죄를 짓다 σ ) + ∂ n σ ∂ σ ( 2 ( 코쉬 τ − cas σ ) 징징거리다 τ ) + ∂ n σ ∂ τ ( − 2 ( 코쉬 τ − cas σ ) 죄를 짓다 σ ) + … 왼쪽. +{\frac {\partial n_{\tau }}{\partial \sigma }}(-(\cosh \tau -\cos \sigma )\sin \sigma )+{\frac {\partial n_{\sigma }}{\partial \sigma }}(2(\cosh \tau -\cos \sigma )\sinh \tau )+{\frac {\partial n_{\sigma }}{\partial \tau }}(-2(\cosh \tau -\cos \sigma )\sin \sigma )+\ldots \right. }
+ ∂ n ϕ ∂ ϕ ( − 2 ( 코쉬 τ − cas σ ) ( 1 − 코쉬 τ cas σ ) 징징거리다 2 τ ) + ∂ 2 n τ ∂ τ 2 ( 코쉬 τ − cas σ ) 2 + ∂ 2 n τ ∂ σ 2 ( − ( 코쉬 τ − cas σ ) 2 ) + … 왼쪽. +{\frac {\partial n_{\phi }}{\partial \phi }}\left({\frac {-2(\cosh \tau -\cos \sigma )(1-\cosh \tau \cos \sigma )}{\sinh ^{2}\tau }}\right)+{\frac {\partial ^{2}n_{\tau }}{{\partial \tau }^{2}}}(\cosh \tau -\cos \sigma )^{2}+{\frac {\partial ^{2}n_{\tau }}{{\partial \sigma }^{2}}}(-(\cosh \tau -\cos \sigma )^{2})+\ldots \right. }
+ ∂ 2 n τ ∂ ϕ 2 ( 코쉬 τ − cas σ ) 2 징징거리다 2 τ } 왼쪽. +{\frac{\frac}{2}n_{\tau }}{{{\n1}n_{\pi }^{2}}:{\frac {(\cosh \tau -\cos \cos \fla )^{2}}:{\sinh ^{2}\}}\오른쪽\}}}}}}}}}}}}}}}}}}}}}}}}}}
+ 1 a 2 e → σ { n τ ( − ( 코쉬 2 τ + 1 − 2 코쉬 τ cas σ ) 죄를 짓다 σ 징징거리다 τ ) + n σ ( − 징징거리다 2 τ − 2 죄를 짓다 2 σ ) + … {\displaystyle +{\frac {1}{a^{2}}}{\vec {e}}_{\sigma }\left\{n_{\tau }\left(-{\frac {(\cosh ^{2}\tau +1-2\cosh \tau \cos \sigma )\sin \sigma }{\sinh \tau }}\right)+n_{\sigma }\left(-\sinh ^{2}\tau -2\sin ^{2}\sigma \right)+\ldots \right. }
+ ∂ n τ ∂ τ ( 2 죄를 짓다 σ ( 코쉬 τ − cas σ ) ) + ∂ n τ ∂ σ ( − 2 징징거리다 τ ( 코쉬 τ − cas σ ) ) + … 왼쪽. +{\frac {\partial n_{\tau }}{\partial \tau }}(2\sin \sigma (\cosh \tau -\cos \sigma ))+{\frac {\partial n_{\tau }}{\partial \sigma }}\left(-2\sinh \tau (\cosh \tau -\cos \sigma )\right)+\ldots \right. }
+ ∂ n σ ∂ τ ( ( 코쉬 τ − cas σ ) ( 1 − 코쉬 τ cas σ ) 징징거리다 τ ) + ∂ n σ ∂ σ ( − ( 코쉬 τ − cas σ ) 죄를 짓다 σ ) + … 왼쪽. +{\frac {\partial n_{\sigma }}{\partial \tau }}\left({\frac {(\cosh \tau -\cos \sigma )(1-\cosh \tau \cos \sigma )}{\sinh \tau }}\right)+{\frac {\partial n_{\sigma }}{\partial \sigma }}(-(\cosh \tau -\cos \sigma )\sin \sigma )+\ldots \right. }
+ ∂ n ϕ ∂ ϕ ( 2 ( 코쉬 τ − cas σ ) 죄를 짓다 σ 징징거리다 τ ) + ∂ 2 n σ ∂ τ 2 ( 코쉬 τ − cas σ ) 2 + ∂ 2 n σ ∂ σ 2 ( 코쉬 τ − cas σ ) 2 + … 왼쪽. +{\frac {\partial n_{\phi }}{\partial \phi }}\left(2{\frac {(\cosh \tau -\cos \sigma )\sin \sigma }{\sinh \tau }}\right)+{\frac {\partial ^{2}n_{\sigma }}{{\partial \tau }^{2}}}(\cosh \tau -\cos \sigma )^{2}+{\frac {\partial ^{2}n_{\sigma }}{{\partial \sigma }^{2}}}(\cosh \tau -\cos \sigma )^{2}+\ldots \right. }
+ ∂ 2 n σ ∂ ϕ 2 ( ( 코쉬 τ − cas σ ) 2 징징거리다 2 τ ) } 왼쪽. +{\frac {\frac }{2}n_{\\properties \phi }^{2}}:\left \frac {(\cosh \tau -\cos \pos \frac )^{2}}:{\sinh ^{2}\}}}\오른쪽\}}}}}}}}}}}}}}}}}}}}
+ 1 a 2 e → ϕ { n ϕ ( − ( 코쉬 τ − cas σ ) 2 징징거리다 2 τ ) + ∂ n τ ∂ ϕ ( 2 ( 코쉬 τ − cas σ ) ( 1 − 코쉬 τ cas σ ) 징징거리다 2 τ ) + … {\displaystyle +{\frac {1}{a^{2}}}{\vec {e}}_{\phi }\left\{n_{\phi }\left(-{\frac {(\cosh \tau -\cos \sigma )^{2}}{\sinh ^{2}\tau }}\right)+{\frac {\partial n_{\tau }}{\partial \phi }}\left({\frac {2(\cosh \tau -\cos \sigma )(1-\cosh \tau \cos \sigma )}{\sinh ^{2}\tau }}\right)+\ldots \right. }
+ ∂ n σ ∂ ϕ ( − 2 ( 코쉬 τ − cas σ ) 죄를 짓다 σ 징징거리다 τ ) + ∂ n ϕ ∂ τ ( ( 코쉬 τ − cas σ ) ( 1 − 코쉬 τ cas σ ) 징징거리다 τ ) + … 왼쪽. +{\frac {\partial n_{\sigma }}{\partial \phi }}\left(-{\frac {2(\cosh \tau -\cos \sigma )\sin \sigma }{\sinh \tau }}\right)+{\frac {\partial n_{\phi }}{\partial \tau }}\left({\frac {(\cosh \tau -\cos \sigma )(1-\cosh \tau \cos \sigma )}{\sinh \tau }}\right)+\ldots \right. }
+ ∂ n ϕ ∂ σ ( − ( 코쉬 τ − cas σ ) 죄를 짓다 σ ) + ∂ 2 n ϕ ∂ τ 2 ( 코쉬 τ − cas σ ) 2 + … 왼쪽. +{\frac {\partial n_{\phi }}{\partial \sigma }}(-(\cosh \tau -\cos \sigma )\sin \sigma )+{\frac {\partial ^{2}n_{\phi }}{{\partial \tau }^{2}}}(\cosh \tau -\cos \sigma )^{2}+\ldots \right. }
+ ∂ 2 n ϕ ∂ σ 2 ( 코쉬 τ − cas σ ) 2 + ∂ 2 n ϕ ∂ ϕ 2 ( ( 코쉬 τ − cas σ ) 2 징징거리다 2 τ ) } 왼쪽. +{\frac {\partial ^{2}n_{\phi }}{{\partial \sigma }^{2}}}(\cosh \tau -\cos \sigma )^{2}+{\frac {\partial ^{2}n_{\phi }}{{\partial \phi }^{2}}}\left({\frac {(\cosh \tau -\cos \sigma )^{2}}{\sinh ^{2}\tau }}\right)\right\}}
Other differential operators such as ∇ ⋅ F {\displaystyle \nabla \cdot \mathbf {F} } ∇ × F {\displaystyle \nabla \times \mathbf {F} } ( σ , τ , ϕ ) {\displaystyle (\sigma ,\tau ,\phi )} orthogonal coordinates .
토로이드 고조파 표준분리 3변수 라플라스 방정식
∇ 2 Φ = 0 {\displaystyle \nabla ^{2}\Phi =0} 변수의 분리 를 통해 용액을 승인한다. 대체하기
Φ = U 코쉬 τ − cas σ {\displaystyle \Phi =U{\sqrt {\cosh \tau -\coses \sigma}} 그런 다음 분리 가능한 방정식을 구한다. 변수의 분리 에 의해 얻어지는 특정한 해결책은 다음과 같다.
Φ = 코쉬 τ − cas σ S ν ( σ ) T μ ν ( τ ) V μ ( ϕ ) {\displaystyle \Phi ={\sqrt {\cosh \tau -\coses \sigma }\,\,S_{\nu }(\sigma ) T_{\mu \nu }(\tau )V_{\mu }(\phi )} 여기서 각 함수는 다음과 같은 선형 조합이다.
S ν ( σ ) = e i ν σ a n d e − i ν σ {\displaystyle S_{\nu }}(\sigma )=e^{i\nu \sigma \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,},\^{-i\nu\nu \sigma}}}}}}} T μ ν ( τ ) = P ν − 1 / 2 μ ( 코쉬 τ ) a n d Q ν − 1 / 2 μ ( 코쉬 τ ) {\displaystyle T_{\mu \nu \}(\tau )=P_{\nu -1/2}^{\mu }}^{\cosh \tau )\\}(\cosh \tau )\}(\coshtau }). V μ ( ϕ ) = e i μ ϕ a n d e − i μ ϕ {\displaystyle V_{\mu }}(\phi )=e^{i\mu \pi \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\^{-i\mu \pi }}}}}} 여기서 P와 Q는 제1종과 제2종의 레전드르 함수와 연관 된다. 이 레전드르 함수는 흔히 토로이드 고조파라고 불린다.
토로이드 고조파들은 많은 흥미로운 성질을 가지고 있다. 변수 치환 cosh > 1 displaysty =\cosh \tau 순서 μ = {\displaystyle \mu 0}, ν {\displaysty \nu =0}
Q − 1 2 ( z ) = 2 1 + z K ( 2 1 + z ) {\displaystyle Q_{-{\frac {1}{1}:{1}2}}(z)={\sqrt {\prac {2}{1+z}}}K\왼쪽({\sqrt {\2}{1+z}}\오른쪽)}} 그리고
P − 1 2 ( z ) = 2 π 2 1 + z K ( z − 1 z + 1 ) {\displaystyle P_{-{\frac {1}{1}:{2}}(z)={\frac {2}{\pi }{{\pi }}{\sqrt {2}{1+z}}}K\{\sqrt {\z-1}}\오른쪽)} 여기 [\displaystyle \,\! K } {\displaystyle \,\! E} 제1종 과 제2종 의 완전한 타원형 통합 이다. 예를 들어, 완전한 타원형 통합의 관점에서, 관련 레전드르 함수에 대한 반복 관계를 사용하여 나머지 토로이드 고조파를 얻을 수 있다.
토로이드 좌표의 고전적 적용은 부분 미분 방정식 (예: 토로이드 좌표가 변수의 분리 를 허용하는 라플라스 방정식 또는 토로이드 좌표가 변수의 분리를 허용하지 않는 헬름홀츠 방정식 )을 해결하는 데 있다. 대표적인 예가 전도성 토러스(torus)의 전위 와 전기장 또는 변질된 경우 전류 링(Hulme 1982년)이다.
대체 분리 또는 다른 대체가 이루어질 수 있다(Andrews 2006).
Φ = U ρ {\displaystyle \Phi ={\frac {U}{\sqrt{\rho}}}}}}} 어디에
ρ = x 2 + y 2 = a 징징거리다 τ 코쉬 τ − cas σ . {\displaystyle \rho ={\sqrt {x^{2}+y^{2} }}}}={\frac {a\sinh \tau }{\cosh \tau -\coses \cosma }}}. } 다시 분리 가능한 방정식을 구한다. 변수 의 분리에 의해 얻어진 특정 해결책은 다음과 같다.
Φ = a ρ S ν ( σ ) T μ ν ( τ ) V μ ( ϕ ) {\displaystyle \Phi ={\frac {a}{\\sqrt{\rho }}\,\,S_{\nu }(\sigma ) T_{\mu \nu }(\tau )V_{\mu }(\phi )} 여기서 각 함수는 다음과 같은 선형 조합이다.
S ν ( σ ) = e i ν σ a n d e − i ν σ {\displaystyle S_{\nu }}(\sigma )=e^{i\nu \sigma \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,},\^{-i\nu\nu \sigma}}}}}}} T μ ν ( τ ) = P μ − 1 / 2 ν ( 나무늘보 τ ) a n d Q μ − 1 / 2 ν ( 나무늘보 τ ) {\displaystyle T_{\mu \nu}(\tau )=P_{\\mu -1/2}^{\nu}^{\cot \tau )\\\\(\cot \tau )\nu {and}\,\,\,\,\,\. V μ ( ϕ ) = e i μ ϕ a n d e − i μ ϕ . {\displaystyle V_{\mu }(\phi )=e^{i\mu \phi \}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,},},} T 함수에 토로이드 고조파(toroidal harmonics)가 다시 사용되지만 인수는 cosh τ displaystyle \coh \tau } cot τ displaystyle \mu \nu } 이 방법은 충전된 링, 무한 반쪽 평면 또는 두 개의 평행 평면과 θ {\displaystyle \theta } 논쟁 쌍곡선 코사인 과대곡선 코사인과 논쟁 쌍곡선 코사인과 관련된 정체성은 위플 공식 을 참조한다.
참조 참고 문헌 목록 Morse P M, Feshbach H (1953). Methods of Theoretical Physics, Part I . New York: McGraw–Hill. p. 666. Korn G A, Korn T M (1961). Mathematical Handbook for Scientists and Engineers . New York: McGraw-Hill. p. 182. LCCN 59014456 . Margenau H, Murphy G M (1956). The Mathematics of Physics and Chemistry 190 –192. LCCN 55010911 . Moon P H, Spencer D E (1988). "Toroidal Coordinates (η , θ , ψ )". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (2nd ed., 3rd revised printing ed.). New York: Springer Verlag. pp. 112–115 (Section IV, E4Ry). ISBN 978-0-387-02732-6 외부 링크 





































![{\begin{aligned}\nabla ^{2}\Phi ={\frac {\left(\cosh \tau -\cos \sigma \right)^{{3}}}{a^{{2}}\sinh \tau }}&\left[\sinh \tau {\frac {\partial }{\partial \sigma }}\left({\frac {1}{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \sigma }}\right)\right.\\[8pt]&{}\quad +\left.{\frac {\partial }{\partial \tau }}\left({\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}{\frac {\partial \Phi }{\partial \tau }}\right)+{\frac {1}{\sinh \tau \left(\cosh \tau -\cos \sigma \right)}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}\right]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e074c8d486891935bf6a90052141f76617b6f440)




































 아니라
아니라



