유사도(기하학)

유클리드 기하학에서, 두 물체는 같은 모양을 갖거나, 한 물체는 다른 물체의 거울 상과 같은 모양을 갖으면 유사하다.보다 정확하게는, 다른 한쪽에서 균일한 스케일링(확대 또는 축소)을 실시해, 번역, 회전, 반사를 추가할 수 있습니다.즉, 한 객체의 크기를 다른 객체와 정확히 일치하도록 조정, 위치 변경 및 반영할 수 있습니다.두 개체가 유사한 경우, 각각은 다른 개체의 특정 균일한 스케일링 결과와 일치합니다.

번역.

회전

반사

스케일링

예를 들어, 모든 원은 서로 비슷하고, 모든 정사각형은 서로 비슷하며, 모든 정삼각형은 서로 비슷합니다.반면, 타원형이 모두 비슷한 것은 아니며, 직사각형도 모두 비슷한 것은 아니며, 이등변 삼각형이 모두 비슷한 것은 아니다.

삼각형의 두 각도가 다른 삼각형의 두 각도의 측도와 같으면 삼각형이 비슷합니다.유사한 폴리곤의 대응변은 비례하고, 유사한 폴리곤의 대응각은 동일한 척도를 가진다.

두 개의 합동 모양은 척도 계수가 1인 유사합니다.하지만, 몇몇 학교 교과서는 삼각형이 ^{[citation needed]}유사한 것으로 인정되려면 크기가 달라야 한다고 주장함으로써 유사한 삼각형의 정의에서 합동 삼각형을 특별히 제외한다.

유사한 삼각형

두 삼각형인 △ and와 △AbBcC,는 해당 각도의 측정값이 동일한 경우에만 유사합니다. 이는 해당 변의 길이가 ^[1]비례하는 경우에만 유사함을 의미합니다.합동각(등각삼각형)을 가진 두 개의 삼각형이 유사하다는 것을, 즉 대응하는 변이 비례한다는 것을 증명할 수 있다.이를 AAA 유사성 ^[2]정리라고 합니다."AAA"는 니모닉이며, 3개의 A 각각은 "각도"를 나타냅니다.이 정리 때문에, 몇몇 저자들은 대응하는 세 개의 각도가 ^[3]일치하도록 요구하기 위해 유사한 삼각형의 정의를 단순화한다.

두 삼각형이 비슷해지려면 각각 필요하고 충분한 몇 가지 기준이 있습니다.

• 유클리드 기하학에서 두 쌍의 ^[4]합각은 모두 ^[5]합각임을 의미한다.

「BAC」가 「B」A」C와 같고, 「ABC」가 「A」B」C와 같다면, 「ACB」가 「A」C」B와 같으며, 삼각형이 같은 것을 의미한다.

• 해당하는 모든 변은 ^[6]비례합니다.

.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-out.넣다 .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}AB′B′)BC′C′)AC′C′.이것은 하나의 삼각형(또는 그것의 거울상)이 다른 삼각형의 확대라고 말하는 것과 같다.

• 두 변의 쌍은 비례하며, 이들 변 사이에 포함되는 각도는 ^[7]일치합니다.

AB/AbB′ = BC/B′C and, ABC는 AbBcC in와 같다.

이를 SAS 유사성 ^[8]기준이라고 합니다."SAS"는 니모닉입니다. 두 개의 S 각각은 "변"을 나타내고 A는 두 개의 변 사이의 "각도"를 나타냅니다.

상징적으로 두 삼각형의 유사성과 차이점을 적습니다△ABC 및 △A'B'C'는 다음과 같습니다.^[9]

$(\displaystyle ABC\sim A'B'C')$

$(\displaystyle ABC\nsim A'B'C')$

유클리드 ^[10]기하학의 유사한 삼각형에 관한 몇 가지 기본적인 결과가 있다.

• 어떤 두 개의 정삼각형도 비슷하다.
• 세 번째 삼각형과 유사한 두 개의 삼각형은 서로 유사합니다(삼각형의 유사성의 전이성).
• 유사한 삼각형의 대응하는 고도는 대응하는 변과 같은 비율을 가진다.
• 두 개의 직각 삼각형은 빗변과 다른 한 변의 길이가 같은 ^[11]비율인 경우 유사합니다.이 경우 동일한 측정값의 예각을 가진 직각 삼각형이나 다리(측면)의 길이가 동일한 비율인 것과 같은 몇 가지 동등한 조건이 있습니다.

삼각형 △CJB 및 선분 DE가 주어지면 눈금자와 나침반을 사용하여 △CJB ~ △DEF가 되는 점 F를 찾을 수 있습니다.이 조건을 만족시키는 점 F가 존재한다는 진술은 월리스의 가정이며^[12] 논리적으로 유클리드의 평행 ^[13]가정과 동등하다.쌍곡기하학(월리스의 가설이 거짓인 경우)에서 유사한 삼각형은 합동입니다.

George David Birkhoff에 의해 주어진 유클리드 기하학의 공리 처리(Birkhoff의 공리 참조)에서, 위에 주어진 SAS 유사성 기준은 유클리드 평행 공리와 힐베르트 ^[8]공리의 극적인 단축을 가능하게 한 SAS 공리를 대체하기 위해 사용되었다.

유사한 삼각형은 유클리드 기하학에서 (좌표를 사용하지 않고) 많은 합성 증명의 기초를 제공한다.이러한 방식으로 증명될 수 있는 기본적인 결과로는 각도 이등분선 정리, 기하 평균 정리, 체바 정리, 메넬라오스 정리, 피타고라스 정리 등이 있다.유사한 삼각형은 직각 삼각 삼각 ^[14]삼각법의 기초를 제공합니다.

기타 유사한 폴리곤

유사성의 개념은 세 개 이상의 변을 가진 다각형으로 확장됩니다.유사한 두 개의 폴리곤이 주어졌을 때, 동일한 시퀀스로 찍은 해당 변(한 폴리곤은 시계방향, 다른 폴리곤은 시계반대방향일지라도)은 비례하고 동일한 시퀀스로 찍은 해당 각도는 측정에서 동일하다.그러나 대응하는 변의 비례성만으로는 삼각형을 넘는 다각형에 대한 유사성을 입증하기에 충분하지 않다(그렇지 않으면 모든 마름모꼴이 유사할 수 있다).마찬가지로, 시퀀스에서 모든 각도의 동일성은 유사성을 보장하기에 충분하지 않습니다(그렇지 않으면 모든 직사각형은 유사합니다).폴리곤의 유사성에 대한 충분한 조건은 대응하는 변과 대각선이 비례한다는 것입니다.

지정된 n에 대해 모든 일반 n-gon은 유사합니다.

유사 곡선

여러 유형의 곡선에는 해당 유형의 모든 예가 서로 유사하다는 특성이 있습니다.여기에는 다음이 포함됩니다.

• 행(임의의 2행은 짝수)
• 선분
• 서클
• 포물선^[15]
• 특정^[16] 이심률의 쌍곡선
• 특정 편심^[16] 타원
• 용병
• 여러 기저값에 대한 로그 함수 그래프
• 서로 다른 기저에 대한 지수 함수 그래프
• 로그 나선형은 자기 유사합니다.

유클리드 공간에서

유클리드 공간의 유사성(유사성 변환 또는 유사성이라고도 함)은 모든 거리에 동일한 양의 실수 r을 곱하는 공간으로부터 그 자신으로의 바이젝션 f이다, 그래서 우리는 임의의 두 점 x와 y에 대해

${\displaystyle d(f(x),f(y)}=r,d(x,y),}$

여기서 "d(x,y)"는 x에서 ^[17]y까지의 유클리드 거리이다.스칼라 r에는 유사도 비율, 신장 계수 및 유사도 계수를 포함한 많은 이름이 있습니다.r = 1일 때 유사성을 등각도(등각 변환)라고 합니다.2개의 세트가 유사성이 있는 다른 세트의 이미지일 경우 유사하다고 불립니다.

지도 f : θⁿ → δ로서ⁿ 비율 r의 유사성은 다음과 같다.

${\displaystyle f(x)=rAx+t,}$

여기서 A o_n O(Ω)는 n × n 직교 행렬이고 t ∈ ℝⁿ ℝ는 변환 벡터이다.

유사성은 평면, 선, 수직도, 평행도, 중간점, 거리와 ^[18]선분 사이의 부등식을 보존한다.유사성은 각도를 보존하지만 반드시 방향을 보존하는 것은 아니며, 직접 유사체는 방향을 보존하고 반대 유사체는 ^[19]이를 변경한다.

유클리드 공간의 유사성은 유사성 그룹 ^[20]S라고 불리는 구성의 작용 하에 그룹을 형성한다.직접 유사체는 S의 정규 부분군을 형성하고 등각체의 유클리드 군 E(n)도 정규 ^[21]부분군을 형성한다.유사도 그룹 S 자체는 아핀 그룹의 부분군이므로 모든 유사도는 아핀 변환입니다.

유클리드 평면을 복소 평면,^[22] 즉 실재 위에 있는 2차원 공간으로 볼 수 있다.2D 유사도 변환은 복잡한 산술의 관점에서 표현될 수 있으며 f(z) = az + b(직접 유사도) 및 f(z) = az + b(직접 유사도)로 표현된다. 여기서 a와 b는 복소수, a ≤ 0이다.a = 1일 때 이러한 유사성은 등각선입니다.

면적비 및 용적비

유사한 도형의 영역 간 비율은 해당 도형의 해당 길이 비율의 제곱과 같다(예를 들어, 정사각형의 변이나 원의 반지름에 3을 곱하면 해당 면적에 9를 곱한다(즉, 3의 제곱).유사한 삼각형의 고도는 대응하는 변과 같은 비율입니다.삼각형이 길이 b의 변과 길이 h의 변으로 그려진 고도를 갖는 경우, 길이가 kb인 해당 변을 가진 유사한 삼각형은 길이 kh의 변으로 그려진 고도를 갖게 된다.첫 번째 삼각형의 면적은 A = 1/2µ이고, 유사한 삼각형의 면적은 A = 1/2(kb)(kh) = kA가² 될 것이다.유사한 삼각형으로 분해할 수 있는 유사한 그림에도 동일한 방식으로 관련된 영역이 있습니다.그 관계는 수정할 수 없는 수치에도 적용된다.

유사한 도형의 부피 간의 비율은 해당 도형의 해당 길이 비율의 세제곱과 같다(예를 들어, 입방체의 모서리 또는 구체의 반지름에 3을 곱하면 부피에는 27을 곱한다). 즉, 3개의 입방체를 곱한다.

갈릴레오의 정사각형-입방체 법칙은 비슷한 고체들을 다룬다.고체 간의 유사성(대응변 비율)의 비율이 k일 경우, 고체 표면적의 비율은 k인² 반면 부피의 비율은³ k가 된다.

중심과의 유사성

유사성에 불변점이 딱 하나 있는 경우, 즉 유사성이 변하지 않는 점을 유사성의 "중심"이라고 합니다.

왼쪽의 제목 아래 첫 번째 이미지에서 하나 또는 다른 유사성으로 인해 정다각형은 각각 이전 다각형 한쪽에 있는 동심원으로 축소됩니다.이 회전 감소가 반복되므로 초기 폴리곤은 일반 폴리곤의 나락으로 확장됩니다.유사성의 중심은 연속된 폴리곤의 공통 중심입니다.빨간색 세그먼트는 유사도 하에서 초기 폴리곤의 정점을 해당 이미지에 결합하고, 이어서 빨간색 세그먼트가 정점의 다음 이미지로 이동하는 등 나선형을 형성한다.사실 이 첫 번째 이미지에서 세 가지 이상의 직접적인 유사점을 볼 수 있습니다. 왜냐하면 모든 정다각형은 어떤 직접적인 유사점에서는 불변하기 때문입니다. 보다 정확하게는 다각형 중심을 회전시키는 특정한 회전, 그리고 직접적 유사점의 구성 또한 직접적인 유사점입니다.$예$를 들어, ${\displaystyle \text{음}}$의 비율$,$ \$displaystyle${text{$ratio}}-k,\}$의 동치 하에 있는 초기 정규 오각형 이미지를 볼 수 있습니다. 이 오각형은 ±180° 각도의 유사성과 k$.\displaystyle {text{$ratio$}}$$k$와 ${\displaystyle 같은}$ 양의 ${\displaystyle \text{비율}}$입니다.$}$

오른쪽 제목 아래 두 번째 이미지는 회전과 동질성으로 분해된 유사성을 보여줍니다.유사도와 회전의 각도는 +135도 모듈로 360도로 동일합니다.유사성과 호모테티의 ${\displaystyle \text{비율}}$은 ${\displaystyle \frac{\mathrm{}}{}}$$displaystyle$$\text{of }}, {\frac {sqrt$ {$2}},$ ${\text$ {$ratio }}},$ {\$sqrt {2}},$ $${\sqrt {2}}, {\}의 제곱근)과 ${\displaystyle 같습니다}$.S점은 회전, 균질성 및 유사성의 세 가지 변환의 공통 중심입니다.${\displaystyle \text{예}}$를 들어 점 W는 회전 중인 F의 이미지이고, 점 T는 호모테티 아래의 W의 이미지입니다${\displaystyle .}$ 보다 간략하게는 T = H (W ) = H (${\displaystyle F}$ ) =$$D (F ) = D ( F ) 、 D ( F ) $style R$ ;$(\displaystyle\text{"}D,\text{\text}) "Direct"$$와 같이 표시됩니다.$$}},},}$

삼각형 EFA를 삼각형 ATB로 변환하는 이 직접적인 유사성은 여러 가지 방법으로 동일한 중심 S의 회전과 동질성으로 분해될 수 있다.$예$를 들어 D ${\displaystyle =}$ ${\displaystyle R\; h}$ H ${\displaystyle =}$ ${\displaystyle H\; r}$R , \$displaystyle$ D , = , $R$, \ $circ$, H , = , $H$, \ $circ$ " , R ,$$} 마지막$$ 분해는 이미지에만 표시됩니다.$D$$({displaystyle$$$D})를$$ $얻기{\displaystyle }$ 위해 $({$의 회전과${\displaystyle \frac{}{}}$비율 $.$ ({$displaystyle${\$text {of$ ratio $}}},{\frac {-{\sqrt {2}}}}}}$의 균질성을 ${\displaystyle 원하는}$ 순서로 구성할 수도 있습니다.$}$

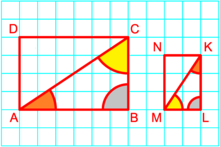
"${\displaystyle M\text{"}}$이 "$"$과 같은 "${\displaystyle M}$$"{$displaystyle$}{\text{}},$ "$거울$$"{\displaystyle }$과 같은 "$I$${\displaystyle \text{"}}$와 "$Indirect"$와 같은 $"{\text{}$와 같이 $"{\displaystyle }$M$\$ M$"$이 M에 대한 반사일 $경우{\displaystyle }$, "WC"와 같은 "I"는 $Indisplaystyle\text{"$와 같습니다$.$$I\;}$는$$D와 ${\displaystyle 같은}$ 세그먼트($BF)$를 ${\displaystyle \text{세그먼트}}$($CT)$로 변환하지만 점 E는 B로, 점 A는 A 자체로 변환하는 간접적인 유사성입니다.정사각형 ACBT는 ${\displaystyle 비율\mathrm{}}$1/${\displaystyle 2}$의${\displaystyle \text{유사도 I}}$의 ABEF 이미지입니다$.$ {\$displaystyle$ I, {\$text{ 비율 }}\;1,/{\sqrt {2}}.$$\;}$ 점 A는 이 유사성의 중심입니다. 왜냐하면 점 K 아래에 불변하는 점 K는 ${\displaystyle \mathrm{AK}}$ $=$ ${\displaystyle K}$/ ${\displaystyle 2\sqrt{\mathrm{}}}$,${\$ AK,=, $AK/{\sqrt {2}},\;}$를 $충족$하기 때문입니다. 그렇지 않으면 ${\displaystyle AK\mathrm{}}$${\displaystyle =}$ $0,$ {\$displaystyle$ {$t {}},K,$0,\}이$$($가{\displaystyle }$ 입력)인 ${\displaystyle \text{경우}}$에만 가능합니다.

${\displaystyle 직사각형}$ ${\displaystyle A}$ ${\displaystyle E}$ $,$ \$displaystyle\text{from$ square$}}}, ABEF,\}$에서 직접 $유사성$의 중심$$${\displaystyle \text{S}}$를 구축하는 방법 선 [SE]를 선 [SA]로 변환하는 +135° 회전의 중심 S를 찾는 방법이것은 내접각 문제와 방향성에 대한 질문입니다.${\displaystyle \theta \mathrm{}\stackrel{}{P}}$ E ${\displaystyle \to }$ , ${\displaystyle P\stackrel{}{}}$ ${\displaystyle \stackrel{}{A}}$ ${\displaystyle \to }$ + ${\displaystyle {135}^{}}$ ${\displaystyle \circ {}^{}}$ { $displaystyle$ P , { \ $text$ { } \ ; { \ angle \ ; { \ $overrightarrow { PA$ } } ,$=$ , + , $135$^ { \ $circ$ $}$ } {\ {\ {\ {\ {\ {\ （ \ ${\displaystyle \stackrel{}{\mathrm{displaystyle}}}$ P , { \ text { \ $text$ { \ } } } } } } } ） ） ） {\ {\ {\ ） {\ {\ {\ {\ {\ EA$}}\;}$는 E와 A를 연결하는 두 개의 반지름이${\displaystyle 2^{}}$의 ${\displaystyle 중심각\mathrm{}}$(180µ${\displaystyle {}^{}}$- ${\displaystyle {\mathrm{135\mu }}^{}}$ $=$ × ${\displaystyle {\mathrm{45\mu }}^{}={}^{}}$ $.$ (\$displaystyle {text${ $of }}\; 2$, ($180^{,\$displaystyle },-135$^{,\class$},\,\,\class$})의 중심$을 형성합니다$.$중앙 F의 사각 ABEF 안쪽에 있습니다.마찬가지로 점 S는 정사각형 BCAT 내의 중심 T의 원의 파란색 1/4의 부재이다.그래서 S점이 이 두 원의 교차점입니다.

일반 메트릭 공간

일반적인 미터법 공간 (X, d)에서, 정확한 유사성은 미터법 공간 X에서 모든 거리에 f의 수축 계수라고 불리는 동일한 양의 스칼라 r을 곱하는 함수 f이다. 그래서 우리는 임의의 두 점 x와 y에 대해

${\displaystyle d(x),f(y)=rd(x,y),}$

예를 들어 유사성이 약한 버전은 f가 bi-Lipschitz 함수이고 스칼라 값이 제한됩니다.

$\displaystyle \lim {d(f(x), f(y)}}, {d(x,y)}=r}$

이 약한 버전은 메트릭이 위상적으로 자체 유사한 집합에서 효과적인 저항일 때 적용됩니다.

미터법 공간의 자기 유사 부분 집합(X, d)은 K가 X의_s 고유한 콤팩트 부분 집합인 수축 계수 0 ≤ r < 1을 갖는 유한한 유사체 {f_s }_s∈S가 존재하는 집합이다.

두 개의 직유체 z'=0.1[(4+i)z+4] 및 z'=0.1[(4+7i)z*+5-2i]로 구성된 자체 유사 집합

$\displaystyle \bigcup _{s\in S}f_{s}(K)=K.,}$

이러한 자기유사 집합은 다음 공식에 의해 주어진 차원 D와 자기유사 측도^D μ를 가진다.

$\displaystyle \sum _{s\in S}(r_{s})^{D}=1,}$

이것은 종종 (항상 그렇지는 않지만) 세트의 하우스도르프 치수 및 패킹 치수와 동일하다.f_s(K) 사이의 중첩이 "작음"인 경우, 다음과 같은 간단한 측정 공식이 있습니다.

$\displaystyle \mu ^{D}(f_{s_{1})\circ f_{s_{2}}\cdots \cdots f_{n}(K)=(r_{s_{1}}\cdot r_{s_{n}})^{D},}.$

토폴로지

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2018년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

토폴로지에서는 거리 대신 유사성을 정의함으로써 메트릭 공간을 구성할 수 있습니다.유사성은 두 점이 가까울 때 값이 더 커지도록 하는 함수입니다(거리와는 반대로, 점이 가까울수록 거리가 작습니다).

유사성의 정의는 원하는 특성에 따라 저자마다 다를 수 있습니다.기본 공통 속성은 다음과 같습니다.

1. 정의:

   $\displaystyle \forall (a,b), S(a,b)\geq 0}$

2. 한 요소의 유사성 자체(자동 유사성):

   $\displaystyle S(a,b)\leq S(a,a)\leq {and}\quad \forall(a,b), S(a,b)=S(a,a)\왼쪽 화살표 a=b}$

반사율(${\displaystyle a}$( ${\displaystyle \text{a}}$, b${\displaystyle }$) ${\displaystyle S}$( ${\displaystyle a}$ ,${\displaystyle }$b ) $=$ S (${\displaystyle b}$ ,$a$ , a$$)\ $displaystyle \forall$ ( a , $b$)\ $S$ $( a$ , b $)\}$또는 finiteness ( ( , ) $$b , $a$,b $display$style s ($all$ ) a , b )상한값은 종종 1로 설정된다(유사성의 확률론적 해석 가능성 생성).

여기서 사용되는 토폴로지적인 의미에서 유사성은 일종의 척도라는 점에 유의하십시오.이 용도는 이 기사의 in유클리드 공간 및 in일반 미터법 공간 섹션의 유사도 변환과 동일하지 않다.

자기유사성

자기유사성은 패턴이 그 자체와 거의 유사하지 않다는 것을 의미합니다ⁱ. 예를 들어 {…, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 12, …} 형식의 숫자 집합은 i가 모든 정수에 걸쳐ⁱ 있는 경우입니다.이 집합을 로그 척도로 표시하면 1차원 변환 대칭이 됩니다. 이 숫자 중 하나의 대수에 2의 대수를 더하거나 빼면 다른 숫자의 대수가 생성됩니다.주어진 숫자의 집합 자체에서 이는 숫자를 2로 곱하거나 나누는 유사성 변환에 해당합니다.

심리학

이 섹션은 확장해야 합니다.여기에 추가하시면 도움이 됩니다. (2021년 7월)

기하학적 유사성의 개념에 대한 직관은 이미 ^[23]그들의 그림에서 볼 수 있듯이 인간의 아이들에게서 나타난다.

「 」를 참조해 주세요.

• 일치(기하학)
• 해밍 거리(문자열 또는 시퀀스 유사성)
• 헬머트 변환
• 반전 기하학
• 자카드 지수
• 비례성
• 기본비례성 정리
• 의미적 유사성
• 유사성 검색
• 유사성(철학)
• 수치 분류법의 유사성 공간
• 호모에이드(동심원, 유사한 타원체 껍질)
• 삼각형의 해

메모들

레퍼런스

• Henderson, David W.; Taimiņa, Daina (2005). Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.). Pearson Prentice-Hall. ISBN 978-0-13-143748-7.
• Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. ISBN 0-7167-0456-0.
• Pedoe, Dan (1988) [1970]. Geometry/A Comprehensive Course. Dover. ISBN 0-486-65812-0.
• Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries. Addison-Wesley. ISBN 978-0-201-87450-1.
• Smart, James R. (1998). Modern Geometries (5th ed.). Brooks/Cole. ISBN 0-534-35188-3.
• Stahl, Saul (2003). Geometry/From Euclid to Knots. Prentice-Hall. ISBN 978-0-13-032927-1.
• Venema, Gerard A. (2006). Foundations of Geometry. Pearson Prentice-Hall. ISBN 978-0-13-143700-5.
• Yale, Paul B. (1968). Geometry and Symmetry. Holden-Day.

추가 정보

• Cederberg, Judith N. (2001) [1989]. "Chapter 3.12: Similarity Transformations". A Course in Modern Geometries. Springer. pp. 183–189. ISBN 0-387-98972-2.
• 콕서터, H. S. M. (1969) [1961]"55 유클리드 평면의 유사성." 페이지 67-76."77 유클리드 공간의 등각과 유사성." 페이지 96~104.지오메트리 소개John Wiley & Sons.
• Ewald, Günter (1971). Geometry: An Introduction. Wadsworth Publishing. pp. 106, 181.
• Martin, George E. (1982). "Chapter 13: Similarities in the Plane". Transformation Geometry: An Introduction to Symmetry. Springer. pp. 136–146. ISBN 0-387-90636-3.

외부 링크

• 유사한 삼각형의 애니메이션 데모