멀티그리드법

수치해석에서는 다변량법(MG법)은 분산의 계층구조를 이용한 미분방정식을 풀기 위한 알고리즘이다. 그것들은 다중화 방법이라고 불리는 기법의 한 종류인데, 복수의 행동 척도를 나타내는 문제에서 매우 유용하다. 예를 들어, 많은 기본적인 이완 방법은 단파장과 장파장 구성요소에 대해 서로 다른 수렴 속도를 보이며, 다중 파장에 대한 푸리에 분석 접근법에서와 같이 이러한 서로 다른 척도를 다르게 취급할 것을 제안한다.^[1] MG 방법은 전제조건뿐만 아니라 해결사로서도 사용될 수 있다.

멀티그리드(multigrid)의 주요 개념은 거친 문제를 해결함으로써 달성한 미세 그리드 용액 근사치의 글로벌 보정에 의해 기본 반복법(단파장 오차를 일반적으로 감소시키는 이완법으로 알려져 있다)의 수렴을 가속화하는 것이다. 거친 문제는 해결 비용이 저렴하지만 장파장 오류와 단파장 오류가 있다는 점에서 미세 그리드 문제와 유사하다. 그것은 또한 이완과 여전히 더 강력한 그리드에 호소하는 것의 결합으로 해결될 수 있다. 이 재귀적 과정은 그리드에 도달할 때까지 반복된다. 그리드는 직접 해결 비용이 미세 그리드의 1회 이완 스위프 비용에 비해 무시할 수 있다. 이 다중 지시 주기는 일반적으로 미세한 그리드 메쉬 크기와는 무관하게 1보다 훨씬 낮은 고정된 양만큼 모든 오류 구성요소를 감소시킨다. 멀티그리드의 일반적인 적용은 2차원 이상의 타원 부분 미분방정식의 수치해법에 있다.^[2]

멀티그리드 방법은 일반적인 디크리트 기법과 조합하여 적용할 수 있다. 예를 들어 유한요소법은 다변량법으로서 다시 작성될 수 있다.^[3] 이러한 경우, 멀티그리드 방법은 오늘날 알려진 가장 빠른 솔루션 기법에 속한다. 다른 방법과는 달리, 임의의 영역과 경계 조건을 처리할 수 있다는 점에서 다변적 방법이 일반적이다. 그들은 방정식의 분리 가능성이나 방정식의 다른 특수 속성에 의존하지 않는다. 그것들은 또한 라메 탄성 방정식이나 Navier-Stokes 방정식과 같이 방정식의 더 복잡한 비대칭 및 비선형 시스템에 널리 사용되어 왔다.^[4]

알고리즘.

빠른 O(n) 수렴을 위한 반복 멀티그리드 알고리즘의 시각화.

멀티그리드 알고리즘에는 여러 가지 변형이 있지만, 공통적인 특징은 디크리트화(그리드)의 계층화를 고려한다는 것이다. 중요한 단계는 다음과 같다.^[5][6]

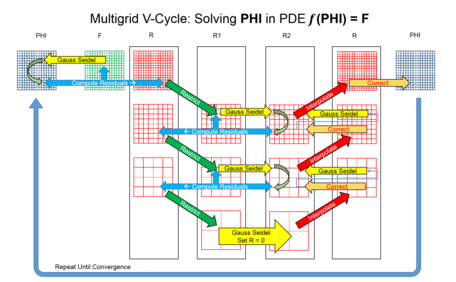
• 평활 – 예를 들어 Gauss-Seel 방법을 몇 번 반복 사용하는 등 고주파 오류를 줄인다.
• 잔차 계산 – 스무딩 작업 후 계산 잔차 오류
• 제한 – 잔여 오차를 코어저 그리드로 다운샘플링
• 보간 또는 연장 – 광학 그리드에서 계산된 보정을 보다 미세한 그리드로 보간.
• 보정 – 연장된 코어 그리드 용액을 더 미세한 그리드에 추가

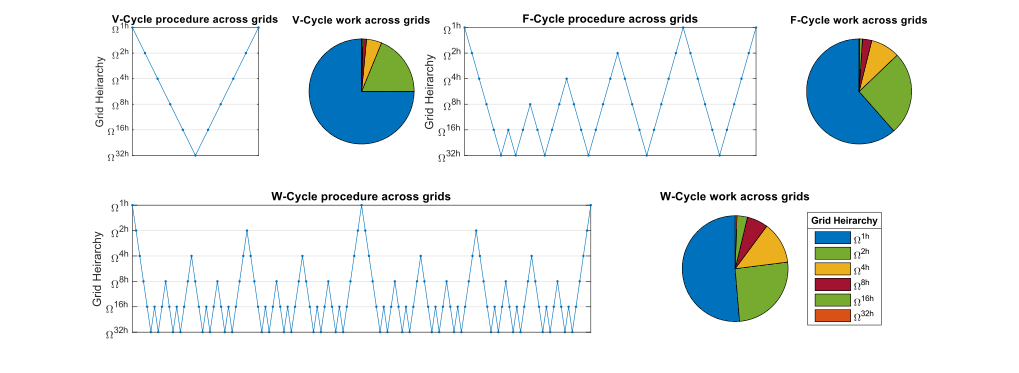
단일 반복을 해결하는 속도와 해당 반복과의 정합화 속도 사이에는 여러 가지 절충이 있는 다중 반복 방법의 선택이 있다. 3가지 주요 유형은 V-Cycle, F-Cycle, W-Cycle이다. 이산형 2D 문제의 경우, F-Cycle은 V-Cycle 반복보다 계산에 83% 더 많은 시간이 걸리는 반면 W-Cycle 반복은 125% 더 많이 걸린다. 문제가 3D 도메인에 설정된 경우, F-Cycle 반복과 W-Cycle 반복이 오버헤드를 무시하는 V-Cycle 반복보다 각각 64%와 75%의 시간이 더 소요된다. 일반적으로 W-Cycle은 F-Cycle과 유사한 융합을 생성한다. 단, Péclet 수치가 높은 대류-확산 문제의 경우, W-Cycle은 F-Cycle에 비해 반복당 수렴율에서 우위를 보일 수 있다. 스무딩 오퍼레이터의 선택은 크릴로프 아공간 방법을 포함하고 있어 매우 다양하며, 전제될 수 있다.

모든 기하학적 다중 주기 반복은 그리드의 계층 구조에서 수행되므로 재귀법을 사용하여 코드화할 수 있다. 함수는 크기가 작은(코어저) 매개변수로 자신을 호출하므로, 가장 큰 격자는 재귀가 정지하는 곳이다. 시스템 상태 번호가 높은 경우, 보정 절차는 연장된 코어저 그리드 용액의 일부만 더 미세한 그리드에 추가되도록 수정된다.

function phi = V_Cycle(phi,f,h)  % Recursive V-Cycle Multigrid for solving the Poisson equation (\nabla^2 phi = f) on a uniform grid of spacing h  % Pre-Smoothing  phi = smoothing(phi,f,h);  % Compute Residual Errors  r = residual(phi,f,h);  % Restriction  rhs = restriction(r);  eps = zeros(size(rhs));  % stop recursion at smallest grid size, other가장 작은_grid_size_is_accieveed eps = 스무딩(eps,rhs,2*h), 다른 eps = V_Cycle(eps,rhs,2*h), % 연장 및 보정 phi = phi + 연장(eps), %-Smooting ph = 스무딩 종료(phi,f,h), 

function phi = F_Cycle(phi,f,h)  % Recursive F-cycle multigrid for solving the Poisson equation (\nabla^2 phi = f) on a uniform grid of spacing h  % Pre-smoothing  phi = smoothing(phi,f,h);  % Compute Residual Errors  r = residual(phi,f,h);  % Restriction  rhs = restriction(r);  eps = zeros(size(rhs));  % stop recursion at smallest grid size, otherwise continue recursion  if smallest_grid_size_is_achieved  eps = smoothing(eps,rhs,2*h);  else  eps = F_Cycle(eps,rhs,2*h);  end  % Prolongation and Correction  phi = phi + prolongation(eps);  % Re-smoothing  phi = smoothing(phi,f,h);  % Compute residual errors  r = residual(phi,f,h);  % Restriction  rhs = restriction(r);  % stop recursion at smal격자 크기를 제외하고 가장 작은_grid_size_is_accieved eps = 평활(eps,rhs,2*h), 다른 eps = V_Cycle(eps,rhs,2*h), 종료 % 연장 및 보정 phi = phi + 연장(eps), %-smooth 후 평활(ph,f,f), 

function phi = W_cycle(phi,f,h)  % Recursive W-cycle multigrid for solving the Poisson equation (\nabla^2 phi = f) on a uniform grid of spacing h  % Pre-smoothing  phi = smoothing(phi,f,h);  % Compute Residual Errors  r = residual(phi,f,h);  % Restriction  rhs = restriction(r);  eps = zeros(size(rhs));  % stop recursion at smallest grid size, otherwise continue recursion  if smallest_grid_size_is_achieved  eps = smoothing(eps,rhs,2*h);  else  eps = W_cycle(eps,rhs,2*h);  end  % Prolongation and correction  phi = phi + prolongation(eps);  % Re-smoothing  phi = smoothing(phi,f,h);  % Compute residual errors  r = residual(phi,f,h);  % Restriction  rhs = restriction(r);  % stop recursion at smal격자 크기를 제외하고 가장 작은_grid_size_is_accieveed eps = 평활(eps,rhs,2*h), 다른 eps = W_cycle(eps,rhs,2*h), % 연장 및 보정 phi = phi + 연장(eps), % 후 평활(phi,f,h); 

계산원가^{[citation needed]}

2차원 문제 설정을 가정하면, 계산은 다양한 멀티그리드 사이클에 대해 그리드 계층 구조에서 다르게 이동한다.

이 접근방식은 종종 사용되는 이산형 노드 수에 따라 선형적으로 확장되는 다른 방법들에 비해 이점이 있다. 즉, 미지의 수에 비례하는 다수의 운용에서 주어진 정확도로 이러한 문제를 해결할 수 있다.

주어진 그리드 포인트 밀도 ${\displaystyle {Ni}_{}}$ ${\$를 가진$$ $그리드{\displaystyle }$ i ${\displaystyle i}$에 대해 (주어진 정확도로) 대략적으로 해결할 수 있는 미분 방정식을 가지고 있다고 가정하고$,$ 또한 $주어진{\displaystyle {}_{}}$ 노력으로 그리드 $N{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$${\displaystyle {}_{}i}$$}$에 대한 솔루션을 얻을 수 있다고$$ 가정한다.${\displaystyle {KN}_{}}$ i {\$displaystyle{\displaystyle }$ $W_{i}=\rho KN_{i}}$은(는) 용액에서 나온$$ 용액 i${\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle$ i$+1$ 여기서 = + 1/ i< ${\displaystyle \rho =N_{i+1}/{i}<1}$는 "근접" 그리드의 격자점 비율이며 그리드 계층 구조 전체에 걸쳐 일정하다고 가정되며 K ${\displaystyle$ K$}$은 $하나$의 격자점에 대한 결과 계산 노력을 일정하게 모델링하는 일부$$ 상수이다.

그런 $다음{\displaystyle }$ 그리드 k ${\displaystyle k}$에서 솔루션을 얻기 위한 노력에 대해 다음과 같은 반복 관계를 얻는다$.$

${\displaystyle W_{k}=W_{k+1}+\rho KN_{k}}$

다른 평활 연산자와 비교한 다중값 사이클의 수렴 비율 예제

그리고 특히, 우리는 가장 훌륭한 그리드 N ${\$}를 찾는다$$.

${\displaystyle W_{1}=W_{2}+\rho KN_{1}.$

이 두 식을 조합하면(${\displaystyle {그리고}_{}}$ N k${\displaystyle {}_{}}$= ${\displaystyle {\rho }^{}}$ ${\displaystyle {}^{}{}_{}}$ -${\displaystyle {}^{}}$1 N ${\displaystyle {1\mathrm{}}_{}}$ ${\$}:{1}:{1}:{1}:{1$\}\}).$

${\displaystyle W_{1}=KN_{1}\sum _{p=0}^{n}\rho ^{p}}}}$

기하학적 시리즈를 사용하여 유한 $n{\displaystyle }$ ${\displaystyle n}$을(를) 찾는다$.$

${\displaystyle W_{1}<KN_{1}{\frac {1}{1-\rho }}$

즉, $O{\displaystyle }$( ${\displaystyle N}$ )${\displaystyle O(N)}$시간$$ 내에 솔루션을 얻을 수 있다. $O{\displaystyle }$( ${\displaystyle N}$) ${\displaystyle O(N)}$ $즉$, O (N)에 대한 한 가지 예외가 있음을 언급해야 한다. 1D 문제에 사용된 W 사이클 멀티그리드: $O{\displaystyle }$( $displaystyle O(Nlog(N)})}$의 복잡성을 야기할 수 있다$.$^{[citation needed]}

멀티그리드 전제 조건화

의도적으로 공차가 감소된 멀티그리드 방법을 외부 반복 해결사의 효율적인 전제조건으로 사용할 수 있다(예:^[7] 용액은 $O{\displaystyle }$( ${\displaystyle N}$) ${\displaystyle O(N)}$회$$, 멀티그리드 방법을 해결사로 사용하는 경우에도 얻을 수 있다. 일반적으로 하이프레와 같은 반복당 하나의 사이클을 갖는 선형 시스템에서도 멀티그리드 전제 조건이 실제로 사용된다. 그것의 주요 장점은 순수하게 다층적인 해결사 대비, 예를 들어 고유치 문제와 같은 비선형적인 문제에서 특히 명확하다.

원래 방정식이나 고유값 문제의 행렬이 대칭 양정확률(SPD)인 경우, 전제조건도 일반적으로 SPD로 구성되므로 표준 결합구배법(CG) 반복법을 계속 사용할 수 있다. 이와 같이 부과된 SPD 제약조건은 전제조건의 건설을 복잡하게 만들 수 있다. 예를 들어 사전 및 사후 스모킹이 조정되어야 한다. 단, SPD 선형 시스템에 대한 전제 조건의 가파른 내리막과 유연한 CG 방법, 대칭 고유값 문제에 대한 LOBPCG는 SPD가 아닌 경우 모두 견고한 것으로 나타난다^[8].

브램블-파시아크-수 전제조건

원래 수의에 박사 학위를 받고 thesis[9]고 나중에 Bramble-Pasciak-Xu,[10]의 BPX-preconditioner은 두명의 주요multigrid 접근법은 과학과 공학에서 모델 설명해의 분할에서 비롯된다 대규모 대수 시스템을 해결하는 것으로(V-cycle과 같은 다른 고전multigrid 알고리즘)출판된다. 부분 미분 방정식 서브공간 보정 프레임워크에서 볼 때,^[11] BPX 전제조건은 병렬 서브공간 보정 방법이며, 고전적인 V 사이클은 연속 서브공간 보정 방법이다. BPX-프리컨테이너는 원래 고전적인 V 사이클 멀티그리드 방식보다 더 병렬적이고 일부 애플리케이션에서는 더 강력한 것으로 알려져 있다. 이 방법은 1990년부터 연구자들과 실무자들이 널리 사용해 왔다.

일반화 다중화 방법

다단계 방법은 여러 가지 방법으로 일반화할 수 있다. 포물선 부분 미분방정식의 타임스텝용액에 자연적으로 적용하거나, 시간 의존적인 부분 미분방정식에 직접 적용할 수 있다.^[12] 쌍곡선 부분 미분 방정식의 다단계 기법에 대한 연구가 진행 중이다.^[13] 멀티그리드 방법은 적분 방정식이나 통계 물리학의 문제에도 적용될 수 있다.^[14]

또 다른 멀티플렉스 방법은 웨이블렛을 기반으로 한다. 이러한 파장 방법은 다중 방식과 결합할 수 있다.^[15][16] 예를 들어, 웨이블렛의 한 가지 용도는 다단계 방법의 관점에서 유한 요소 접근방식을 재조정하는 것이다.^[17]

적응형 멀티그리드(adaptive multigrid)는 적응형 메시 정교함을 보여주는데, 즉 계산이 진행됨에 따라 계산 자체에 의존하는 방식으로 그리드를 조정한다.^[18] 이 아이디어는 그리드가 필요한 솔루션의 영역에서만 그리드의 해상도를 증가시키는 것이다.

대수 멀티그리드(AMG)

다단계 방법의 실질적으로 중요한 확장에는 다단계 계층 구조를 위해 부분적인 미분 방정식이나 기하학적 문제 배경이 사용되지 않는 기법이 포함된다.^[19] 그러한 대수적 다변량 방법(AMG)은 시스템 매트릭스에서 직접 연산자의 계층구조를 구성한다. 고전적인 AMG에서, 계층의 수준은 기하학적 해석 없이 단순히 미지의 하위 집합일 뿐이다. (더 일반적으로, 거친 격자 미지의 경우 미지의 미세한 격자의 특정한 선형 결합일 수 있다.) 따라서 AMG 방법은 희박한 행렬의 특정 계층을 위한 블랙박스 해결기가 된다. AMG는 기하급수적인 멀티그리드(multigrid)를 적용하기 너무 어려운 경우에 주로 유리하다고 여겨지지만,^[20] 단순히 진정한 멀티그리드 구현에 필요한 코딩을 피한다는 이유만으로 자주 사용된다. 고전 AMG가 먼저 개발되었지만, 관련 대수적 방법은 평활집계(SA)라고 알려져 있다.

진차오 쉬와 루드밀 지카타노프의 개요 논문에서는^[21] "알제브라틱 멀티그리드" 방법을 추상적인 관점에서 이해한다. 그들은 통일된 프레임워크를 개발했고 기존의 대수적 다단계 방법은 일관성 있게 도출될 수 있다. 준최적 공간뿐만 아니라 최적의 거친 공간을 구성하는 방법에 대한 추상적 이론이 도출되었다. 또한, 그들은 적절한 가정 하에서 추상적인 2-수준 AMG 방법이 선형 시스템의 크기, 계수 변동 및 음이소트로피와 관련하여 균일하게 수렴된다는 것을 증명하였다. 이들의 추상적 프레임워크는 고전 AMG, 에너지 최소화 AMG, 미수축 및 평활 집적 AMG, 스펙트럼 AMGe 등 대부분의 기존 AMG 방법을 망라하고 있다.

시간 방법의 다중값

또한 초기 가치 문제의 해결을 위해 여러 가지 방법이 채택되었다.^[22] 여기서 특히 관심 있는 것은 병렬 시간 다중 지시법이다:[23] 고전적인 Runge-Kutta 또는 선형 다중 단계 방법과 대조적으로 그것들은 시간적 방향에서 동시성을 제공할 수 있다. 잘 알려진 파라알 병렬인 시간 통합 방식도 시간 내에 2단계 다중값으로 재구성할 수 있다.

거의 특이한 문제에 대한 멀티그리드

거의 특이한 문제들이 많은 중요한 물리적 및 엔지니어링 애플리케이션에서 발생한다. 단순하지만 거의 특이한 문제의 중요한 예는 거의 압축할 수 없는 재료에 대한 선형 탄성의 변위 공식에서 찾을 수 있다. 일반적으로, 거의 단수에 ${\displaystyle \mathrm{가까운}}$ 시스템을 해결하기 위한 주요 문제는 $A{\displaystyle }$+ + ${\displaystyle M}$ ${\displaystyle A+\varepsilon M}$이(가) 제공하는 거의 단수 연산자를 양의 매개 변수 $parameter{\displaystyle }$ ${\displaystyle \varepsilon }$에 대해$$ 강하게 다루기 위해 요약된다$.$ 여기서 $A{\displaystyle }$ ${\displaystystyleder}$은 대칭 반피니트 연산자다.e null 공간인 반면 $M{\displaystyle }$ ${\displaystyle M}$은(는) 대칭 양정확정 연산자임. 그러한 거의 특이한 문제들에 대해 강력하고 빠른 멀티그리드 방법을 설계하려는 많은 작품들이 있었다. 일반적인 지침 하나의 설계 원리로서(예, 그물코 크기와 푸아송 비와 같이 거의 유일한 연산자에 나타나는 물리적 파라미터들)매개 변수를multigrid 메서드에 적용하는 독립적인 융합률을 달성할 제공되고 있어 그런 거의 단수 즉, 각 그리드에서, 우주 분해가 smo 기반 systems,[24].oth거의 단수 연산자의 단수 부분의 null 공간이 로컬 null 공간의 합, null 공간의 교차점 및 공간 분해로 인한 로컬 공간의 합에 포함되도록 ing을 적용해야 한다.

메모들

참조

• G. P. 아스트라찬스프(1971), 타원 그물 문제를 해결하는 반복적인 방법. USSR Comp. 수학. 수학. 체육관 111, 171–182.
• N. S. Bakhvalov(1966)는 타원 연산자에 대한 자연적 제약조건이 있는 이완법의 정합성에 대하여. USSR Comp. 수학. 수학. 체육관 6, 101–13
• Achi Brandt(1977년 4월), "경계-가치 문제에 대한 다단계 적응 솔루션", 연산 수학, 31: 333–90.
• 윌리엄 L. 브릭스, 반 엠든 헨슨, 스티브 F. McCormick(2000), A Multigrid Tutorial(2차 개정), 공업 및 응용 수학 협회, ISBN 0-89871-462-1.
• R. P. Fedorenko (1961년), 타원차 방정식을 풀기 위한 이완법. USSR Compute. 수학. 수학. 체육 1, 1092페이지.
• R. P. Fedorenko(1964년), 하나의 반복적인 과정의 융합 속도. USSR Compute. 수학. 수학. 체육 4, 227쪽
• Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 20.6. Multigrid Methods for Boundary Value Problems". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.

외부 링크

• 다중값, 다중값, 다중값, 집계, 결함 수정 및 도메인 분해 방법의 저장소
• 멀티그리드 자습서
• 대수적 다중 문자 자습서
• AMG 프레젠테이션 링크