저크(물리학)

얼간이
얼간이
	저크를 포함한 위치의 시간적 변이
공통 기호	j, j, ȷ→
SI 기준 단위	m/s3
치수	L T−3

물리학에서 저크나 저크는 물체의 가속도가 시간에 따라 변하는 속도를 말한다. 벡터 수량(규모와 방향을 모두 가지고 있음)이다. 저크는 가장 일반적으로 기호 $j$ 로 표시되며 m/s³(SI 단위) 또는 초당 표준 강도(g₀/s)로 표현된다.

표현.

벡터로서 저크 $j$ 는 가속도의 첫 번째 파생상품, 속도의 두 번째 파생상품 및 위치의 세 번째 파생상품으로 표현될 수 있다.

\mathbf {j} (t)={\frac {\mathrm {d} \mathbf {a} (t)}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf {v} (t)}{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} (t)}{\mathrm {d} t^{3}}}

어디에

a

가속도

v

는 속도다.

r

is position

t

는 시간이다.

폼의 3차 미분 방정식

J\left({\overset {...)}{x},{\ddot{x},{\dot{x},x\right)=0

때때로 얼크 방정식이라고 불린다. 보통 1차 비선형 미분방정식 3개의 등가 시스템으로 변환할 때, 저크 방정식은 혼돈된 행동을 보이는 용액의 최소 설정이다. 이 조건은 저크 시스템에 수학적 흥미를 유발한다. 따라서 4차 파생상품 이상을 포함하는 시스템을 하이퍼저크 시스템이라고 부른다.^[1]

생리적 효과와 인간의 인식

인체의 위치는 적대적 근육의 힘의 균형을 유지함으로써 조절된다. 체중을 지탱하는 것과 같은 주어진 힘의 균형을 유지하는 데 있어서, 중앙 후 회향은 원하는 평형을 달성하기 위한 제어 루프를 설정한다. 힘이 너무 빨리 변하면 근육이 충분히 빠르게 이완되거나 긴장하지 못하고 어느 한 방향으로 오버슈팅해 일시적으로 조절력을 상실하게 된다. 힘의 변화에 반응하기 위한 반응 시간은 생리적 한계와 뇌의 주의 수준에 따라 달라진다: 예상되는 변화는 갑작스러운 부하 감소나 증가보다 더 빨리 안정될 것이다.

차량 탑승자가 신체 움직임에 대한 통제력을 상실하고 부상을 당하지 않도록 근육 장력을 조절하고 제한된 스트레스 변화에도 적응하는 데 시간이 필요하기 때문에 최대 힘(가속)과 최대 저크 양쪽에 대한 노출을 제한할 필요가 있다. 급격한 가속도의 변화는 채찍질 같은 부상을 초래할 수 있다.^[2] 또한 과도한 저크는 부상을 야기하지 않는 수준에서도 불편한 승차감을 유발할 수 있다. 엔지니어들은 엘리베이터, 전차 및 기타 운송 수단에서 "재키 운동"을 최소화하기 위해 상당한 설계 노력을 기울인다.

예를 들어, 차를 탈 때 가속 및 저크 효과를 고려하십시오.

숙련되고 숙련된 운전자들은 부드럽게 가속할 수 있지만 초보자들은 종종 덜컹거리는 승차감을 제공한다. 발로 작동하는 클러치가 장착된 자동차에서 기어를 바꿀 때 엔진 출력에 의해 가속력이 제한되지만, 경험이 부족한 운전자는 클러치 위로 간헐적으로 힘이 닫히기 때문에 심한 저크 현상을 일으킬 수 있다.
고성능 스포츠카를 타고 좌석으로 밀려드는 느낌은 가속도 때문이다. 차가 정지 상태에서 출발할 때 가속도가 급격히 높아지면서 포지티브 저크(positive juff)가 커진다. 발사 후 자동차의 속도에 따라 공기저항의 힘이 증가하여 가속도가 점차 감소하고 승객을 좌석으로 누르는 힘이 감소함에 따라 작고 지속적인 저크(negative juck)가 있다. 차량이 최고 속도에 도달하면 가속도가 0에 도달하여 일정하게 유지되며, 그 후에는 운전자가 감속하거나 방향을 변경할 때까지 저크가 발생하지 않는다.
갑자기 제동하거나 충돌하는 동안 제동할 때, 근육 장력이 제동 시작 또는 충돌 후 신속하게 신체에 대한 제어력을 회복하기 때문에 승객들은 나머지 제동 과정 동안보다 더 큰 초기 가속도로 앞으로 채찍질한다. 시체와 충돌 시험 인체모형에는 능동적인 근육 조절 기능이 없기 때문에 이러한 효과는 차량 시험에서 모형화되지 않는다.

힘, 가속 및 저크

일정한 질량 $m$ 의 경우 가속도 $a$ 는 뉴턴의 두 번째 운동 법칙에 따라 힘 $F$ 에 정비례한다.

{\mathbf {F}=m\cdot {\mathbf {a}

강체 신체의 고전적 역학에서 가속의 파생물과 관련된 힘은 없지만 물리적 시스템은 저크에 의한 진동과 변형을 경험한다. NASA는 허블우주망원경을 설계하면서 저크와 저스트 모두에 제한을 두었다.^[3]

아브라함-로렌츠 힘은 가속 충전된 입자 방출 방사선에 대한 반동력이다. 이 힘은 입자의 당김과 전하의 제곱에 비례한다. 휠러-파인만 흡수기 이론은 보다 발전된 이론으로, 상대적 환경과 양자적 환경에 적용되며, 자기 에너지에 대한 회계처리가 가능하다.

이상화된 설정에서

가속의 불연속은 변형, 양자역학 효과 및 기타 원인에 의해 실제 환경에서는 발생하지 않는다. 단, 가속도의 점프-불연속성 및 그에 따라 한없는 저크는 조각처럼 매끄러운 전체 연속 경로를 따라 움직이는 이상적인 점 질량과 같은 이상적인 환경에서 실현 가능하다. 점프-지속성은 경로가 매끄럽지 않은 지점에서 발생한다. 이러한 이상화된 설정에서 추론해 보면 실제 상황에서 얼간이 효과를 정성적으로 기술, 설명 및 예측할 수 있다.

가속도의 점프-지속성은 점프 높이로 스케일링된 저크 단위의 Dirac 델타 함수를 사용하여 모델링할 수 있다. Dirac 델타에 걸쳐 시간에 따른 저크 통합은 점프-지속성을 산출한다.

예를 들어, $반지름$ r의 호를 따라 직선으로 접선되는 경로를 고려하십시오. 전체 길은 연속적이고, 조각은 매끄럽다. 점 입자가 이 경로를 따라 일정한 속도로 이동하므로 접선 가속도가 0이라고 가정해 보십시오. 그 구심 가속도.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .d에 의해 주어집니다.En{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}v2/r은 아크와 안쪽으로는 것이 일반적이다. 입자가 조각들의 연결을 통과할 때, $v 2 / r$ 에 의해 주어진 가속도에서 점프-지속성을 경험하고, 점프-지속성에 맞춰 Dirac 델타에 의해 모델링될 수 있는 저크를 경험한다.

불연속 가속도의 보다 가시적인 예를 위해 마찰과 함께 이상적인 표면에서 질량이 진동하는 이상적인 스프링-매스 시스템을 고려한다. 질량에 가해지는 힘은 스프링 힘과 운동 마찰력의 벡터 합과 같다. 속도가 부호(최대 및 최소 변위)를 변경할 때 질량에 가해지는 힘의 크기가 마찰력의 2배만큼 변화하는데, 이는 스프링력이 연속적이고 마찰력이 속도에 따라 방향을 역전시키기 때문이다. 가속도 점프는 질량을 질량으로 나눈 힘과 같다. 즉, 질량이 최소 또는 최대 변위를 통과할 때마다 질량은 불연속 가속을 경험하고, 저크는 질량이 멈출 때까지 디락 델타를 포함한다. 정적 마찰력은 잔류 스프링력에 적응하여 순하중 0과 속도 0으로 평형을 이룬다.

제동 및 감속 자동차의 예를 들어보자. 브레이크 패드는 휠의 디스크(또는 드럼)에 운동 마찰력과 지속적인 제동 토크를 발생시킨다. 회전 속도는 일정한 각도 감속과 함께 선형적으로 0으로 감소한다. 마찰력, 토크, 자동차 감속은 갑자기 0에 도달하는데, 이는 물리적인 저크에서 디락 델타가 있음을 나타낸다. Dirac 델타는 실제 환경에 의해 평활화되며, 그 누적 효과는 생리학적으로 인지된 멍청이들의 감쇠와 유사하다. 이 예는 타이어 슬라이딩, 서스펜션 디핑, 모든 이상적으로 견고한 메커니즘의 실제 변형 등의 영향을 무시한다.

첫 번째 예와 유사하게, 상당한 얼간이의 또 다른 예는 끝에 입자가 있는 밧줄을 자르는 것이다. 입자가 0이 아닌 구심 가속도의 원형 경로에서 진동한다고 가정하십시오. 밧줄이 끊어지면 입자의 경로가 일직선으로 갑자기 바뀌고, 안쪽으로 향하는 힘이 갑자기 0으로 바뀐다. 레이저에 의해 절단된 단분자 섬유를 상상해 보십시오. 이 입자는 매우 짧은 절단 시간 때문에 매우 높은 수의 저크 현상을 경험할 수 있을 겁니다.

교대로

작동 중인 4위치 외부 제네바 드라이브를 보여주는 애니메이션

각도, 각도 속도, 각도 가속도 및 각도 저크에 대한 1회전 이상의 타이밍 다이어그램

관성 기준 프레임에서 고정 축을 중심으로 회전하는 강체 본체를 고려한다. 시간의 함수로서 각도 위치가 $θ (t$ )인 경우, 각도 속도, 가속도 및 저크는 다음과 같이 표현할 수 있다 $.$

각도 속도, $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ( t $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ) $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ = $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ t $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ) $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ = $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ( $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ) $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ ${\$ }}(t $)={\frac {\mathrm$ { $d} \d}}}}}$ 는 $\omega (t)={\dot {\theta }}(t)={\frac {\mathrm {d} \theta (t)}{\mathrm {d} t}}$ $θ (t$ )의 시간 파생물이다 $.$
각도 가속도, $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ ) = $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ ( $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ ) $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ = $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ ( t $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ ) t ${\$ 은 $\alpha (t)={\dot {\omega }}(t)={\frac {\mathrm {d} \omega (t)}{\mathrm {d} t}}$ $t)$ 의 시간 파생이다 $.$
각저크, $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ( t $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ) $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ = $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ( $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ) $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ = $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ( $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ) $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ = $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ . $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ . . $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ . ( $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ ) ${\dot \jeta (t)={\dot {\omega }}}(t)={\ddot {\$ dote $}}(t)={\overset {...$ $}{\teta }}}}$ 은 $\zeta (t)={\dot {\alpha }}(t)={\ddot {\omega }}(t)={\overset {...}{\theta }}(t)$ 는) $α (t$ )의 시간 파생물이다 $.$

각도 가속은 몸에 작용하는 토크를 말하며, 순간적인 회전 축에 대한 몸의 관성 모멘트로 나눈다. 토크의 변화로 인해 각저크가 발생한다.

회전 강체 차체의 일반적인 경우는 하나의 축방향 벡터, 각도 속도 $Ω (t)$ 및 하나의 극방향 벡터, 선형 $속도$ v $(t$ )를 포함하는 키네마틱 나사 이론을 사용하여 모델링할 수 있다 $.$ 여기서 각 가속도는 다음과 같이 정의된다.

{\boldsymbol {\alpha }}(t)={\frac {\mathrm {d} t}{\mathrm {d} t}{\boldsymbol {\}(t)={\dot {\boldsymbol {\}}}(t)}}}

그리고 각진 멍청이들은 다음에 의해 주어진다.

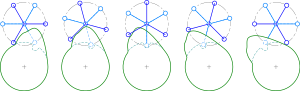
{\boldsymbol {\zeta }}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {\alpha }}(t)={\dot {\boldsymbol {\alpha }}}(t)={\ddot {\boldsymbol {\Omega }}}(t)

예를 들어, 제네바 드라이브를 고려해 보십시오. 제네바 드라이브는 구동 휠(애니메이션의 빨간색 휠)을 연속적으로 회전시켜 구동 휠(애니메이션의 파란색 휠)을 간헐적으로 회전시키는 데 사용되는 장치입니다. 구동 휠의 한 사이클 동안 구동 휠의 각도 위치 $θ$ 90도 변화한 다음 일정하게 유지된다. 구동 휠 포크(주행 핀의 슬롯)의 유한 두께 때문에 이 장치는 각도 가속도 $α$ 에 불연속성을 발생시키고 구동 휠에 무한 각 저크 $ζ$ 을 발생시킨다.

저크는 제네바 드라이브가 영화 프로젝터나 캠과 같은 애플리케이션에서 사용되는 것을 막지 않는다. 영화 프로젝터의 경우 필름은 프레임별로 진척되지만 프로젝터 작동은 소음이 적고 필름 부하(필름 몇 그램의 작은 부분만 구동)와 중간 속도(2.4m/s), 마찰이 적어 신뢰성이 높다.

듀얼 캠 드라이브

혁명당 6분의1

1회전당3분의 1

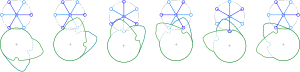
캠 구동 시스템의 경우 듀얼 캠을 사용하면 단일 캠의 저크 현상을 피할 수 있지만 듀얼 캠은 부피가 더 크고 비용이 더 많이 든다. 듀얼 카메라 시스템은 한 차축에 캠 2개가 달려 있어 두 번째 차축을 회전 단위로 이동시킨다. 그림은 구동축의 1회전당 1/6회 및 1/3회전의 스텝 구동력을 보여준다. 스텝드 휠의 두 암이 항상 이중 캠과 접촉하기 때문에 방사상 간극이 없다. 일반적으로 결합 접점은 단일 추종자와 관련된 저크(그리고 마모 및 소음)를 피하기 위해 사용될 수 있다(예: 슬롯을 따라 미끄러지는 단일 추종자 및 슬롯의 한 쪽에서 다른 쪽으로 접촉점을 변경하는 것은 각각 한 쪽을 따라 미끄러지는 두 팔로워를 사용함으로써 피할 수 있다).

탄성 변형 물질에서

압축파 패턴

평면파

원통대칭

탄성 변형 가능한 질량은 가해진 힘(또는 가속도)에 따라 변형되며, 변형은 그 강성과 힘의 크기 함수다. 힘의 변화가 느리면 저크는 작으며, 가속도의 변화에 비해 변형의 전파를 순간적으로 간주한다. 일그러진 몸은 마치 퀘이시스트 체계에 있는 것처럼 작용하며, 변화력(비제로 저크)만이 기계적 파(또는 충전된 입자에 대한 전자파)의 전파를 일으킬 수 있으므로, 0이 아닌 저크에서 높은 저크까지의 경우 충격파와 몸체를 통한 전파를 고려해야 한다.

변형의 전파는 "압축파 패턴"에 탄성 변형 물질을 통한 압축 평면 파형으로 나타나 있다. 또한 각도 저크의 경우 변형파가 원형 패턴으로 전파되어 전단 응력과 다른 진동 모드를 유발하는 변형파가 표시된다. 경계를 따라 파동을 반사하면 건설적인 간섭 패턴(그림화되지 않음)이 발생하여 재료의 한계를 초과할 수 있는 응력이 발생한다. 변형파는 특히 공명의 경우 진동을 일으켜 소음, 마모, 기능 상실로 이어질 수 있다.

대형톱이 있는 폴

"매시브 탑이 있는 폴"이라는 자막에는 탄성 폴과 매시브 탑이 연결된 블록이 표시된다. 블록이 가속하면 폴이 휘고, 가속이 멈추면 폴이 뻣뻣한 상태로 팽이가 진동(감쇠)한다. 어떤 사람은 작은 진동이 충격파에 의해 강화되기 전에 감쇠되기 때문에 더 큰 (주기적) 저크(buck)가 더 큰 진폭을 자극할 수 있다고 주장할 수 있다. 또한 충격파의 큰 파동 성분은 더 높은 주파수와 푸리에 계수를 가지기 때문에 더 큰 저크가 공명 모드를 흥분시킬 확률을 높일 수 있다고 주장할 수 있다.

사인파 가속도 종단

흥분된 응력파와 진동의 진폭을 줄이기 위해 운동을 형성하고 가능한 평평한 경사면에서 가속을 연속적으로 만들어 저크를 제한할 수 있다. 추상 모델의 한계로 인해 진동을 줄이는 알고리즘에는 Jounce와 같은 상위 파생 모델이 포함되거나 가속과 저크 모두에 대해 연속적인 방식을 제안한다. 저크 제한에 대한 개념 중 하나는 가속과 감속을 0의 가속으로 정현상 형상으로 만드는 것이다(그림 캡션 "Sinusoidal Acceleration Profile" 참조). 속도를 정속도로 정현상 형상으로 한다. 그러나 저크는 가속도가 0 단계로 들어가고 나가는 지점에서 불연속성을 유지한다.

도로와 선로의 기하학적 디자인

선로전환곡선은 저크(buck) 전환은 파란색 직선과 녹색 원호 사이에 빨간색으로 표시된다.

도로와 선로는 곡률 변화에 의해 야기되는 혹을 제한하도록 설계되었다. 철도에서 설계자는 0.35m/s를³ 설계 목표로, 0.5m/s를³ 최대치로 사용한다.^{[citation needed]} 트랙 전환 곡선은 직선에서 곡선으로 전환할 때 저크(저크)를 제한하거나 그 반대의 경우도 제한한다. 호를 따라 일정한 속도 운동에서 저크는 접선 방향에서 0이고 내측 정상 방향에서 0이 아니라는 점을 상기한다. 전환 곡선은 곡면성을 점진적으로 증가시키고 결과적으로 구심 가속도를 증가시킨다.

이론적으로 최적의 전환 곡선인 오일러 나선은 구심 가속도를 선형적으로 증가시키고 일정한 저크 현상을 초래한다(그림 참조). 실제 애플리케이션에서 트랙의 평면은 곡선 구간을 따라 경사(칸트)된다. 경사는 수직 가속을 유발하며, 이는 트랙과 제방의 마모를 위한 설계 고려사항이다. 비너 커브(Viennes Curve)는 이러한 마모를 최소화하기 위해 설계된 특허 곡선이다.^[4]^[5]

롤러코스터는^[2] 또한 선로 전환을 통해 저크를 제한하도록 설계되었다. 루프에 진입할 때 가속도 값은 약 4g(40m/s²)에 이를 수 있으며, 이 높은 가속도 환경에서의 승마는 트랙 전환을 통해서만 가능하다. 그림 8s와 같은 S자형 곡선도 원활한 놀이기구를 위해 트랙 전환을 사용한다.

인모션 컨트롤

모션 제어에서 설계 초점은 한 고정 위치에서 다른 고정 위치(점 대 점 운동)로 시스템을 이동할 필요성과 함께 직선 직선 운동에 집중한다. 저크 관점에서 설계 문제는 수직 저크다. 선형 운동이 회전하지 않기 때문에 접선 가속에서 저크는 사실상 0이다.

동작 제어 애플리케이션에는 승객용 엘리베이터와 가공 도구가 포함된다. 수직 저크 제한은 엘리베이터 탑승 편의를 위해 필수적인 것으로 간주된다.^[6] ISO 18738은^[7] 저크, 가속, 진동 및 소음과 관련하여 엘리베이터 승차 품질에 대한 측정 방법을 명시하지만, 표준은 허용 가능하거나 허용할 수 없는 승차 품질에 대한 수준을 명시한다. 대부분의^[8] 승객들은 2m/s의³ 수직 저크, 6m/s의³ 저크에 대해 허용 가능한 것으로 평가한다고 보고되었다. 병원의 경우 0.7m/s가³ 권장된다.

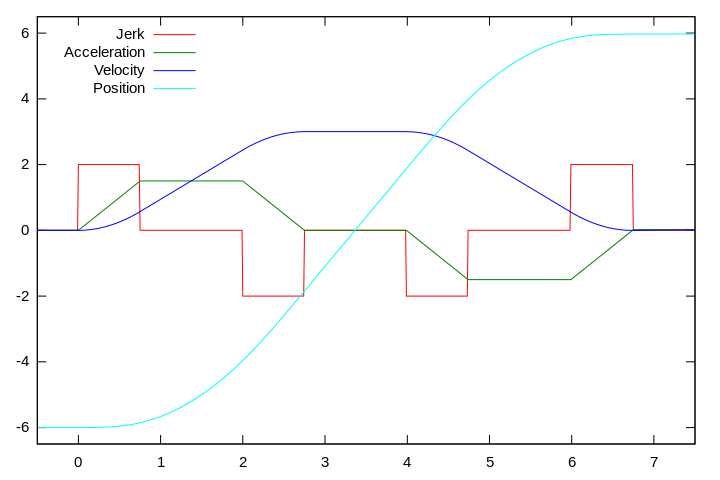
동작 제어를 위한 일차 설계 목표는 속도, 가속도 또는 저크 한계를 초과하지 않고 전환 시간을 최소화하는 것이다. 속도에서 2차 경사로 및 디램핑 단계가 있는 3차 모션 컨트롤 프로필을 고려하십시오(그림 참조).

이 운동 프로파일은 다음과 같은 7개의 세그먼트로 구성된다.

가속 증가 - 양의 저크 한계치, 양의 가속 한계치까지 가속도의 선형 증가, 속도 2차 증가
가속도 상한 - 저크 0, 속도 선형 증가
가속도 하향 - 저크 한계치 음수, 가속도 선형 감소, (음수) 2차 속도 증가, 원하는 속도 제한에 근접
속도 제한 - 저크 없음, 가속 없음
감속 증가 — 저크 음의 한계치, 가속도의 선형 감소, (음) 속도 2차 감소
감속 한계 하한 - 저크 0, 속도 선형 감소
감속 감소 - 양의 저크 한계치, 0으로 가속도의 선형 증가, 속도 2차 감소, 0속도와 0 가속도에서 원하는 위치에 접근

세그먼트 4의 시간(정속)은 두 위치 사이의 거리에 따라 달라진다. 만일 이 거리가 너무 작아서 세그먼트 4를 생략해도 충분하지 않을 경우, 세그먼트 2와 6(정수 가속도)는 동일하게 감소할 수 있으며, 등속 제한에 도달하지 못할 수 있다. 이 수정으로 교차 거리가 충분히 줄어들지 않으면 세그먼트 1, 3, 5, 7이 동일한 양만큼 단축될 수 있으며, 일정한 가속 한계에 도달하지 못할 수 있다.

주어진 전환 시간^[9] 동안 저크 사각형을 최소화하는 것과 같은 다른 동작 프로파일 전략과 위에서 설명한 것처럼 사인파 모양의 가속 프로필이 사용된다. 운동 프로필은 기계, 사람 이동 장치, 체인 호이스트, 자동차, 로봇 공학 등 특정 용도에 맞게 조정된다.

제조에 있어서

저크는 제조 공정에서 중요한 고려사항이다. 절삭 공구의 가속도가 급격하게 변화하면 공구 마모가 조기에 발생하여 균일하지 않은 절단을 초래할 수 있으며, 결과적으로 현대적인 모션 컨트롤러에는 저크 제한 기능이 포함된다. 기계 공학에서 저크는 속도 및 가속도와 더불어 캠 프로파일 개발에서 고려된다. 왜냐하면 역학적 함의와 수다없이 캠 프로파일을 따라갈 수 있는 작동 신체의 능력 때문이다.^[10] 저크는 진동이 우려될 때 종종 고려된다. 저크(buckmeter)를 측정하는 장치를 "저크미터"라고 한다.

추가파생상품

추가 시간 파생상품은 스냅 또는 점스트(4차 파생상품), 크랙클(5차 파생상품), 팝(6차 파생상품)으로 명명되었다.^[11]^[12] 그러나 4개보다 높은 순위의 시간적 파생상품은 거의 나타나지 않는다.^[13]

스냅, 크래클, 팝이라는 용어는 광고 마스코트 스냅, 크래클, 팝에서 영감을 얻었다.^[12]

참고 항목

참조

^ Chlouverakis, Konstantinos E.; Sprott, J. C. (2006). "Chaotic hyperjerk systems" (PDF). Chaos, Solitons & Fractals. 28 (3): 739–746. Bibcode:2006CSF....28..739C. doi:10.1016/j.chaos.2005.08.019.
^ Jump up to: ^a ^b "How Things Work: Roller Coasters - The Tartan Online". Thetartan.org. 2007-04-16. Retrieved 2013-09-15.
^ "Third derivative of position". math.ucr.edu. Retrieved 2019-09-08.
^ https://depatisnet.dpma.de/DepatisNet/depatisnet?window=1&space=menu&content=treffer&action=pdf&docid=AT000000412975B
^ "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-13. Retrieved 2014-08-17.CS1 maint: 제목으로 보관된 복사본(링크)
^ "Archived copy" (PDF). Archived from the original (PDF) on 2014-08-26. Retrieved 2014-08-22.CS1 maint: 제목으로 보관된 복사본(링크)
^ ISO 18738-1:2012. "Measurement of ride quality -- Part 1: Lifts (elevators)". International Organization for Standardization. Retrieved 31 December 2014.
^ Howkins, Roger E. "Elevator Ride Quality - The Human Ride Experience". VFZ-Verlag für Zielgruppeninformationen GmbH & Co. KG. Archived from the original on 14 March 2015. Retrieved 31 December 2014.
^ Hogan, Neville (1984). "An organizing principle for a class of voluntary movements". J. Neurosci. 4 (11): 2745–2754. doi:10.1523/JNEUROSCI.04-11-02745.1984. PMC 6564718. PMID 6502203.
^ Blair, G, "캠 만들기" 레이스 엔진 기술 10, 2005년 9~10월
^ Thompson, Peter M. (March 2011). "Snap, Crackle, and Pop" (PDF). Proc of AIAA Southern California Aerospace Systems and Technology Conference. p. 1. Archived from the original (PDF) on 2017-03-04. Retrieved 29 February 2020. The common names for the first three derivatives are velocity, acceleration, and jerk. The not so common names for the next three derivatives are snap, crackle, and pop.
^ Jump up to: ^a ^b Visser, Matt (31 March 2004). "Jerk, snap and the cosmological equation of state". Classical and Quantum Gravity. 21 (11): 2603–2616. arXiv:gr-qc/0309109. Bibcode:2004CQGra..21.2603V. doi:10.1088/0264-9381/21/11/006. ISSN 0264-9381. S2CID 10468158. Snap [the fourth time derivative] is also sometimes called jounce. The fifth and sixth time derivatives are sometimes somewhat facetiously referred to as crackle and pop.
^ Gragert, Stephanie; Gibbs, Philip (November 1998). "What is the term used for the third derivative of position?". Usenet Physics and Relativity FAQ. Math Dept., University of California, Riverside. Retrieved 2015-10-24.

Sprott JC (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5.
Sprott JC (1997). "Some simple chaotic jerk functions" (PDF). Am J Phys. 65 (6): 537–43. Bibcode:1997AmJPh..65..537S. doi:10.1119/1.18585. Archived from the original (PDF) on 2010-06-13. Retrieved 2009-09-28.
Blair G (2005). "Making the Cam" (PDF). Race Engine Technology (10). Retrieved 2009-09-29.

외부 링크

세 번째 파생상품에 사용되는 용어는 무엇인가? 유센트 물리학 FAQ의 얼간이에 대한 설명
운동 제어 프로필의 수학
엘리베이터-라이드-품질
엘리베이터 제조업체 브로셔
비에너 쿠르브 특허
(독일어로) 비에너 쿠르브 설명

[1] Chlouverakis, Konstantinos E.; Sprott, J. C. (2006). "Chaotic hyperjerk systems" (PDF). Chaos, Solitons & Fractals. 28 (3): 739–746. Bibcode:2006CSF....28..739C. doi:10.1016/j.chaos.2005.08.019.

[thetartan2007-2] Jump up to: ^a ^b "How Things Work: Roller Coasters - The Tartan Online". Thetartan.org. 2007-04-16. Retrieved 2013-09-15.

[3] "Third derivative of position". math.ucr.edu. Retrieved 2019-09-08.

[4] ttps://depatisnet.dpma.de/DepatisNet/depatisnet?window=1&space=menu&content=treffer&action=pdf&docid=AT000000412975B

[5] "Archived copy" (PDF). Archived from the original (PDF) on 2016-03-13. Retrieved 2014-08-17.CS1 maint: 제목으로 보관된 복사본(링크)

[6] "Archived copy" (PDF). Archived from the original (PDF) on 2014-08-26. Retrieved 2014-08-22.CS1 maint: 제목으로 보관된 복사본(링크)

[7] ISO 18738-1:2012. "Measurement of ride quality -- Part 1: Lifts (elevators)". International Organization for Standardization. Retrieved 31 December 2014.

[8] Howkins, Roger E. "Elevator Ride Quality - The Human Ride Experience". VFZ-Verlag für Zielgruppeninformationen GmbH & Co. KG. Archived from the original on 14 March 2015. Retrieved 31 December 2014.

[9] Hogan, Neville (1984). "An organizing principle for a class of voluntary movements". J. Neurosci. 4 (11): 2745–2754. doi:10.1523/JNEUROSCI.04-11-02745.1984. PMC 6564718. PMID 6502203.

[10] Blair, G, "캠 만들기" 레이스 엔진 기술 10, 2005년 9~10월

[11] Thompson, Peter M. (March 2011). "Snap, Crackle, and Pop" (PDF). Proc of AIAA Southern California Aerospace Systems and Technology Conference. p. 1. Archived from the original (PDF) on 2017-03-04. Retrieved 29 February 2020. The common names for the first three derivatives are velocity, acceleration, and jerk. The not so common names for the next three derivatives are snap, crackle, and pop.

[Visser2004-12] Jump up to: ^a ^b Visser, Matt (31 March 2004). "Jerk, snap and the cosmological equation of state". Classical and Quantum Gravity. 21 (11): 2603–2616. arXiv:gr-qc/0309109. Bibcode:2004CQGra..21.2603V. doi:10.1088/0264-9381/21/11/006. ISSN 0264-9381. S2CID 10468158. Snap [the fourth time derivative] is also sometimes called jounce. The fifth and sixth time derivatives are sometimes somewhat facetiously referred to as crackle and pop.

[PhysicsFAQ-13] Gragert, Stephanie; Gibbs, Philip (November 1998). "What is the term used for the third derivative of position?". Usenet Physics and Relativity FAQ. Math Dept., University of California, Riverside. Retrieved 2015-10-24.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Search