부분군
Subgroup이 글은 검증을 위해 인용구가 추가로 필요하다. 그룹– · · · · (2009년 6월)(이 |
수학의 한 분야인 집단 이론에서, 2진법 ∗에 따라 그룹 G가 주어지는 경우, G의 부분집합 H도 연산 ∗에 따라 그룹을 형성하면 G의 부분집합 H라고 부른다. 보다 정확히 말하면, ∗에서 H × H로 제한되는 것이 H에 대한 집단 운영이라면 H는 G의 서브그룹이다. 이것은 보통 H ≤ G로 표시되며, "H는 G의 부분군"으로 읽힌다.
모든 그룹의 사소한 하위 그룹은 ID 요소만으로 구성된 하위 그룹 {e}이다.
그룹 G의 적절한 부분군은 G의 적절한 부분군 H(즉, H ( G)이다. 이것은 일반적으로 H < G로 합리적으로 표현되며, "H는 G의 적절한 하위집단"으로 읽힌다. 일부 저자는 또한 사소한 그룹이 적절하지 않다고 제외한다(즉, H ≠ {e}).[1][2]
H가 G의 부분군이라면 G를 H의 오버그룹이라고 부르기도 한다.
동일한 정의는 G가 임의의 세미그룹일 때 더 일반적으로 적용되지만, 이 글은 그룹의 하위그룹만을 다룰 것이다. 그룹 G는 순서가 정해진 쌍(G, ∗)에 의해 표시되기도 하는데, 대개 G가 복수 대수학이나 다른 구조물을 운반할 때 연산 emphasize을 강조하기 위해서입니다.
부분군의 기본 특성
- 그룹 G의 부분집합 H는 제품 및 반전 아래에 비어 있지 않고 닫힌 경우에만 G의 부분집합이다. (폐쇄조건은 a와 b가 H에 있을 때마다 ab과 a도−1 H에 있다는 것을 의미한다. 이 두 조건은 하나의 동등한 조건으로 결합될 수 있다: a와 b가 H에 있을 때마다 ab도−1 H에 있다.) H가 유한한 경우 H가 제품 아래에서 닫히는 경우에만 H가 부분군이다. (이 경우, H의 모든 원소는 H의 유한 순환 부분군을 생성하며, a의 역은 a = a이고−1n−1, 여기서 n은 a의 순서다.)
- 위의 조건은 동형상이라는 관점에서 진술할 수 있다. 즉, H가 G의 부분집합이고 H에서 G까지의 포함 동형상(즉, i(a) = a)가 있는 경우에만 H가 그룹 G의 부분군이다.
- 부분군의 아이덴티티는 집단의 아이덴티티: G가 아이덴티티 e를G 가진 집단이고 H가 아이덴티티 e를H 가진 G의H 아이덴티티라면 e = eG.
- 부분군에서 원소의 역행은 그룹 내 원소의 역행이다: 만약 H가 그룹 G의 부분군이고, a와 b가 ab = eH, 그리고 ab = ba = e와G 같은 H의 요소라면.
- 부분군 A와 B의 교차점은 다시 부분군이다.[3] 부분군 A와 B의 조합은 예를 들어 2와 3은 2Z와 3Z의 조합이지만 합계는 5가 아니기 때문에 A와 B 중 하나가 다른 하나를 포함하는 경우에만 부분군이다. 다른 예로는 평면 내 x축과 y축의 결합(추가 연산 포함)을 들 수 있다. 이러한 각 개체는 부분군이지만 그 결합은 아니다. 이것은 또한 두 부분군의 예로서, 교차점이 정확히 정체성이다.
- S가 G의 부분 집합인 경우 S를 포함하는 최소 부분군이 존재하며, 이는 S를 포함하는 모든 부분군의 교차점을 취함으로써 찾을 수 있다. 이는 ⟨S⟩에 의해 표시되며 S에 의해 생성된 부분군이라고 한다. G의 원소는 S의 원소와 그 반대로의 유한한 산물인 경우에만 sS⟩에 있다.
- 그룹 G의 모든 원소는 주기적인 부분군 ⟨a⟩을 생성한다. 만약 ⟨a⟩이 어떤 양의 정수 n에 대해 Z/nZ에 이형성이라면, n은 an = e, n을 a의 순서라고 부르는 가장 작은 양의 정수다. 만약 ⟨a⟩이 Z에 이형이라면, a는 무한한 질서를 가지고 있다고 한다.
- 주어진 그룹의 하위 그룹은 하위 그룹의 격자라 불리는 포함 하에서 완전한 격자를 형성한다. (여기서 최소치가 통상적으로 정해진 이론적 교차로인 반면, 하위집단의 집합적 이론적 결합은 집합적 이론적 결합 그 자체가 아니라 하위집단의 이론적 결합에 의해 생성된 부분군이다.) e가 G의 ID인 경우, 사소한 그룹 {e}이(가) G의 최소 하위 그룹인 반면, 최대 하위 그룹은 G 그룹 그 자체인 것이다.
코제트와 라그랑주의 정리
부분군 H와 일부 a를 G로 지정하면 왼쪽 코셋 aH = {ah : h in H}을(를) 정의한다. a는 변위가 불가능하기 때문에 φ(h) = ah가 주는 지도 φ : H → aH는 편향이다. 또한, G의 모든 요소는 정확히 하나의 H의 왼쪽 코셋에 포함되어 있다. 왼쪽 코세트는 a1 ~ a2 if 및1−12 aa가 H에 있는 경우에만 동등성 관계에 해당하는 동등성 등급이다. H의 왼쪽 코세트의 수는 G에서 H의 지수라 불리며 [G : H]로 표시된다.
라그랑주의 정리에는 유한군 G와 부분군 H에 대해
여기서 G와 H는 각각 G와 H의 순서를 나타낸다. 특히 G의 모든 부분군 순서(및 G의 모든 요소의 순서)는 G의 구분자여야 한다.[4][5]
우측 코세트는 다음과 유사하게 정의된다. Ha = {ha : h in H}. 또한 적절한 동등성 관계에 대한 동등성 등급이며 그 수는 [G : H]와 같다.
aH = 모든 a in G에 대해 Ha이면 H는 정상 부분군이라고 한다. 지수 2의 모든 부분군은 정상이다: 왼쪽 코세트와 오른쪽 코세트는 단순히 부분군과 그것의 보완물이다. 보다 일반적으로, p가 유한 그룹 G의 순서를 나누는 최저 프라임이라면, 지수 p의 모든 부분군(있는 경우)은 정상이다.
예제: Z 부분군8
G를 원소가 있는 순환 그룹8 Z로 한다.
그리고 그 그룹 운영은 8번 추가 모듈로 8번. 그것의 Cayley 테이블은
| + | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
| 4 | 4 | 0 | 6 | 2 | 5 | 1 | 7 | 3 |
| 2 | 2 | 6 | 4 | 0 | 3 | 7 | 5 | 1 |
| 6 | 6 | 2 | 0 | 4 | 7 | 3 | 1 | 5 |
| 1 | 1 | 5 | 3 | 7 | 2 | 6 | 4 | 0 |
| 5 | 5 | 1 | 7 | 3 | 6 | 2 | 0 | 4 |
| 3 | 3 | 7 | 5 | 1 | 4 | 0 | 6 | 2 |
| 7 | 7 | 3 | 1 | 5 | 0 | 4 | 2 | 6 |
이 그룹에는 ■ J = {0, 4} 및 ■ H = {0, 4, 2, 6}의 두 개의 비경쟁 하위 그룹이 있으며, 여기서 J도 H의 하위 그룹이다. Cayley 테이블 for H는 Cayley 테이블의 왼쪽 상단 사분면이고, Cayley 테이블은 Cayley 테이블의 왼쪽 상단 사분면이다. G 그룹은 순환적이고, 그 하위 그룹도 순환적이다. 일반적으로 순환집단의 하위집합도 순환집합이다.
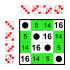
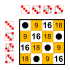
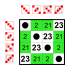
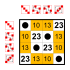
예제: S의4 부분군(4개 원소의 대칭 그룹)
모든 그룹은 주 대각선 상에 중립 요소만큼 많은 작은 하위 그룹을 가지고 있다.
사소한 그룹과2 두 가지 요소 그룹 Z. 이러한 작은 부분군은 다음 목록에 포함되지 않는다.
12원소
8원소
6원소
4원소
 순환군4 Z |
3요소
 순환군3 Z |
기타 예
- 짝수 정수는 정수의 가법 그룹의 부분군이다. 짝수 두 개를 더하면 짝수를 얻게 된다.
- 링 에서 인 것은 R 의 첨가제 그룹의 하위 그룹이다
- 벡터 공간의 선형 하위 공간은 벡터 추가 그룹의 하위 공간이다.
- 을(를) 아벨 그룹으로 한다. 기간이 한 A 의 요소가 의 토션 하위 그룹이라고 불리는 의 하위 그룹을 형성한다
참고 항목
메모들
참조
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
- Hungerford, Thomas (1974), Algebra (1st ed.), Springer-Verlag, ISBN 9780387905181.
- Artin, Michael (2011), Algebra (2nd ed.), Prentice Hall, ISBN 9780132413770.
- Dummit, David S.; Foote, Richard M. (2004). Abstract algebra (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264.





![{\displaystyle [G:H]={|G| \over |H|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)