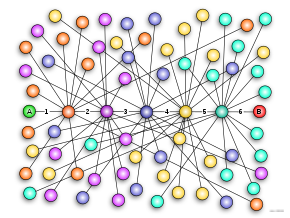소규모 실험

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '소규모 실험'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2008년 3월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

이 작은 세계의 실험은 스탠리 밀그램과 다른 연구원들이 미국 ^[1]사람들의 소셜 네트워크에 대한 평균 경로 길이를 조사하는 몇 가지 실험으로 구성되었다.이 연구는 인간 사회가 짧은 경로 길이로 특징지어지는 작은 세계형 네트워크임을 시사했다는 점에서 획기적인 것이었다.밀그램은 이 용어를 직접 사용하지 않았지만, 실험은 종종 "6단계 분리"라는 문구와 관련이 있다.

작은 세계 문제의 역사적 맥락

1909년 노벨상 ^{[2][failed verification]}수상 연설에서 밝힌 굴리엘모 마르코니의 20세기 초 라디오 작업에 기초한 추측은 헝가리 작가 프리예스 카린시가 기껏해야 5명을 ^[4]통해 연결될 수 없는 다른 사람을 찾기 위한 도전을 쓰도록 자극했을 수도 있다^[3].이것은 아마도 6단계 분리 개념과 작은 세계 문제에 대한 해답을 찾는 것에 대한 최초의 언급일 것이다.

수학자 만프레드 코첸과 정치학자 이티엘 드 솔라 풀은 밀그램이 그들의 연구를 위해 방문했던 1950년대 초 파리 대학에서 일하면서 수학 원고 "연락과 영향"을 썼다.그들의 미공개 원고는 1978년 출판되기 전까지 20년 이상 학계 사이에서 유통되었다.그것은 공식적으로 소셜 네트워크의 역학을 설명하고, 이러한 역학의 수학적 결과(연결성 정도를 포함)를 탐구했다.이 원고는 네트워크에 대한 많은 중요한 의문을 남겼으며, 그 중 하나는 실제 소셜 네트워크에서의 분리 수였다.

밀그램은 파리에서 돌아오면서 도전을 시작했고, 1967년 5월(차터) 인기 잡지 '심리학 투데이'에 실린 '작은 세상 문제'에 실린 실험으로 이어졌고, 2년 뒤 더 엄격한 버전의 논문이 소시오메트리에 실렸다.Psychology Today 기사는 많은 조형 작업이 잊혀진 지 한참 지난 오늘날 잘 알려진 실험에 대해 엄청난 관심을 불러일으켰다.

밀그램의 실험은 세계가 점점 더 상호 연결되고 있다는 생각에 많은 독립적인 스레드들이 모여들던 시대에 고안되었다.Michael Gurevich는 Pool의 MIT 박사학위 논문에서 소셜 네트워크 구조에 대한 경험적 연구를 수행했다.통계 도시 설계에 관여한 오스트리아 수학자 만프레드 코헨은 수학 원고인 Contacts and Influences에서 이러한 경험적 결과를 추론하여, 사회 구조가 없는 미국인 크기의 인구에서, "어떤 두 개인도 다른 방법으로 서로 접촉할 수 있다는 것은 실질적으로 확실하다.두 명의 중개인을 만나다[사회적으로] 구조화된 집단에서는 가능성이 낮지만 여전히 가능성이 있어 보인다.그리고 아마도 전 세계 인구에게는 한 명의 가교자만 ^{[citation needed]}더 필요할 것입니다.그들은 이어서 구레비치의 데이터를 기반으로 몬테카를로 시뮬레이션을 구성했는데, 구레비치는 사회 구조를 모델링하기 위해 약한 지인 연계가 모두 필요하다는 것을 인식했다.1973년의 느린 컴퓨터에서 실행되는 시뮬레이션은 제한적이었지만, 여전히 밀그램의 발견을 암시하는 값인 보다 현실적인 3도 분리가 미국 인구 전체에 존재한다는 것을 예측할 수 있었다.

밀그램은 구레비치가 1967년 하버드 대학에서 시작한 고도로 알려진 일련의 실험을 수행했을 때 지인 네트워크 실험을 다시 방문했다.밀그램의 가장 유명한 작품 중 하나는 복종과 권위에 대한 연구로, 밀그램 ^[5]실험으로 널리 알려져 있다.밀그램은 풀과 코첸과의 초기 연관성은 인간들 간의 상호 연결성 증가에 대한 그의 관심의 원천으로 생각되었다.구레비치의 인터뷰는 그의 작은 세계 실험의 기초가 되었다.

밀그램은 작은 세계의 문제를 해결할 수 있는 실험을 개발하려고 했다.이는 1920년대 작가 프리예스 카린시가 부다페스트에서 개인이 6단계의 사회적 접촉에 의해 분리된다는 널리 퍼진 믿음을 기록하면서 밝힌 것과 같은 현상이다.이 관찰은, 차례로, 그 기간 동안 동유럽 도시 설계에 매우 영향을 미쳤던 통계학자들의 인구통계학적 작업에 느슨하게 기초했다.폴란드에서 태어나 동유럽을 광범위하게 여행한 수학자 Benoit Mandelbrot는 통계의 경험 법칙을 알고 있었으며, 1950년대 초 파리 대학의 Pool, Kochen 및 Milgram의 동료이기도 했다(코첸은 만델브로트를 고등연구소와 나중에 IBM에 데려왔다).이 연구자 그룹은 소셜 네트워크의 상호 연결성과 "소셜 자본"에 매료되었습니다.

밀그램의 연구 결과는 미국 사람들이 지구적 연계에 대해 추측하지 않고 평균적으로 대략 세 개의 우정 연계에 의해 연결되어 있는 것처럼 보인다는 것을 보여주었습니다; 그는 실제로 "분리의 6도"라는 문구를 사용하지 않았습니다.Psychology Today 기사가 실험을 널리 알린 이후, 밀그램, 코첸, 카린시는 모두 "6도"의 개념의 기원으로 잘못 여겨져 왔다. "6도 분리"라는 문구의 가장 유력한 인기인은 "6도"의 가치를 마르코니에게 돌렸다.

실험

밀그램의 실험은 무작위로 선택된 두 사람이 서로를 ^[6]알 수 있는 가능성에 대해 더 알고 싶은 욕망에서 발전했다.이것은 작은 세계의 문제를 바라보는 하나의 방법이다.이 문제에 대한 다른 견해는 모집단을 소셜 네트워크로 상상하고 두 노드 사이의 평균 경로 길이를 찾는 것입니다.밀그램의 실험은 두 사람 사이의 연결 수를 세는 절차를 개발함으로써 이러한 경로의 길이를 측정하기 위해 고안되었다.

기본 절차

1. 실험은 여러 가지 변형을 거쳤지만 밀그램은 전형적으로 미국 네브라스카 오마하와 캔자스 위치타의 개인을 출발점으로, 매사추세츠 주 보스톤을 통신 사슬의 끝점으로 선택했다.이 도시들은 미국에서 사회적,^[4] 지리적으로 매우 먼 거리를 나타낸다고 여겨졌기 때문에 선택되었다.
2. 정보 패킷은 처음에 오마하 또는 위치타에서 무작위로 선택된 개인에게 전송되었습니다.여기에는 연구의 목적을 상세히 기술한 편지와 보스턴의 목표 연락자에 대한 기본 정보가 포함되어 있었다.거기에는 또한 그들이 자신의 이름을 쓸 수 있는 등록부뿐만 아니라 하버드 대학으로 미리 주소가 지정된 업무용 회신 카드도 포함되어 있었다.
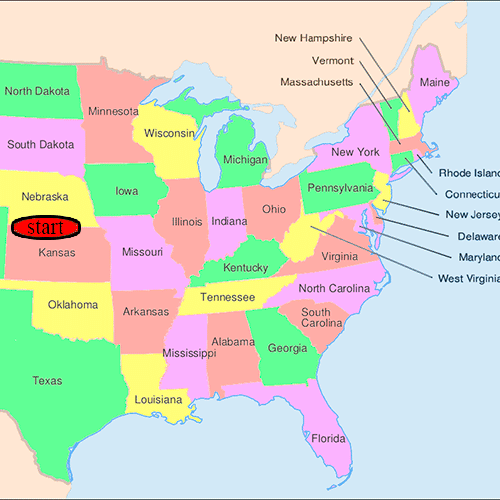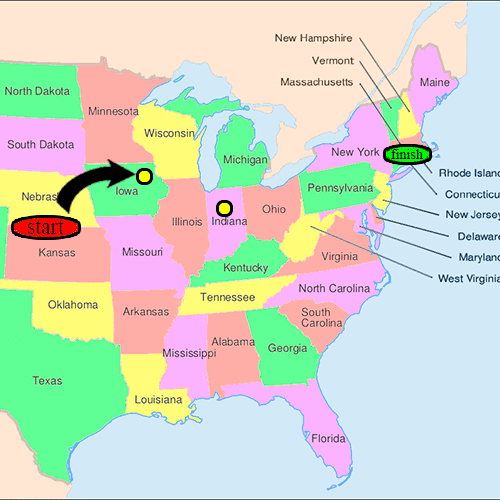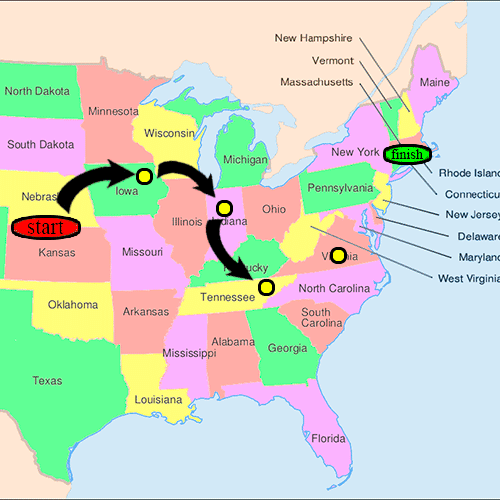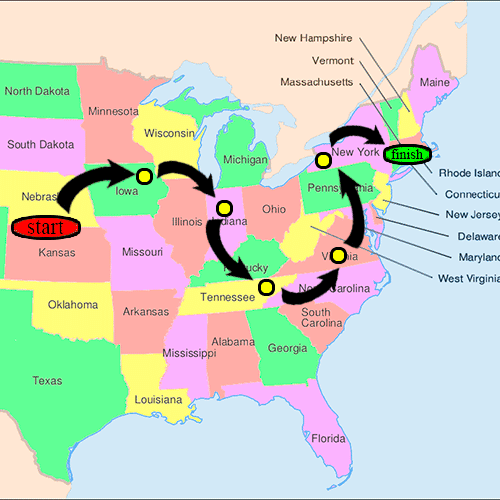
3. 참가 초대를 받은 수신자는 편지에 기재된 연락처와 개인적으로 아는 사이인지 물었다.만약 그렇다면, 그 사람은 그 사람에게 편지를 직접 전달해야 한다.이 연구의 목적상, 누군가를 "개인적으로" 아는 것은 그 사람을 이름만 대면 아는 것으로 정의되었다.
4. 그 사람이 대상을 개인적으로 알지 못하는 경우, 그 사람은 대상을 알 가능성이 높은 친구나 친척을 생각나는 사람은 대상을 알 가능성이 높은 친구나 친척이었다.그리고 나서 그들은 명부에 서명하고 그 사람에게 패킷을 전달하라는 지시를 받았다.목표물을 향한 사슬의 진행을 추적할 수 있도록 하기 위해 하버드 연구자들에게 엽서도 발송되었다.
5. 소포가 보스턴에 있는 연락처에 도달했을 때, 그리고 만약 그 소포가 사람에게서 사람으로 전달된 횟수를 세기 위해 연구진은 명부를 검사할 수 있었다.또한, 도착지에 도착하지 않은 소포의 경우, 들어오는 엽서가 체인의 ^{[citation needed]}중단점을 식별하는 데 도움이 되었습니다.

결과.

실험이 시작된 직후, 편지들이 목표물들에게 도착하기 시작했고 연구원들은 응답자들로부터 엽서를 받았다.경우에 따라서는 패킷이 불과1 홉 또는 2 홉만에 타겟에 도달하는 경우가 있습니다.또한 일부 체인은 9 또는 10개의 링크로 구성되어 있습니다.하지만, 중요한 문제는 종종 사람들이 편지를 전달하기를 거부했고, 따라서 그 체인은 목적지에 도착하지 않았다는 것이다.296통의 편지 중 232통이 ^[6]목적지에 도착하지 않은 경우도 있었다.

그러나 64통의 편지가 결국 목표물과의 접촉에 도달했다.이들 체인 중 평균 경로 길이는 약 5.5에서 6개 정도 감소했습니다.따라서, 연구원들은 미국 사람들이 평균 6명 정도 떨어져 있다고 결론지었다.밀그램 자신도 "6단계 분리"라는 문구를 사용한 적이 없지만, 이러한 발견들이 널리 받아들여지는 ^[4]데 기여했을 가능성이 높다.

160통의 편지를 우송한 실험에서, 24명은 메사추세츠주 샤론의 집에서 목표물에 도달했다.24통의 편지 중 16통은 같은 사람 밀그램이 표적에 건넨 것으로, "제이콥스 씨"라고 불리는 의류 상인이다.그의 사무실에서 목표물에 도달한 사람들 중 절반 이상이 다른 ^[7]두 명의 남자에게서 왔다.

연구원들은 만들어지는 사슬의 종류를 정성적으로 조사하기 위해 엽서를 사용했다.일반적으로 패키지는 지리적으로 가까운 곳에 빠르게 도달했지만 목표물의 내부 친구를 ^[6]찾을 때까지 거의 무작위로 목표물을 돌았다.이는 참가자들이 사슬에서 적절한 다음 사람을 선택할 때 지리적 특성을 강하게 선호했음을 시사한다.

비판

실제로 평균 경로 길이가 밀그램이 예상한 것보다 작거나 클 수 있다는 것을 암시하는 작은 세계 실험에 대한 방법론적인 비판이 많다.이러한 비판은 다음 4가지로 요약된다.

1. Judith Kleinfeld는^[8] Milgram의 연구가 참여자를 모집한 방식과 높은 미완료율 때문에 선택과 무응답 편향으로 인해 어려움을 겪고 있다고 주장한다.첫째, "스타터"들은 무작위로 뽑히지 않았다. 왜냐하면 그들은 특별히 자신들과 연관이 있다고 생각하는 사람들을 찾는 광고를 통해 모집되었기 때문이다.또 다른 문제는 감소율과 관련이 있다.체인의 각 개인에 대해 일정한 무응답 부분을 가정하면, 더 긴 체인은 의도하지 않은 참가자와 마주칠 가능성이 높기 때문에 충분히 표현되지 않을 것이다.따라서 밀그램의 실험은 실제 평균 경로 길이를 과소평가해야 한다.이러한 추정치를 수정하기 위해 여러 가지 방법이 제안되었다. 중단된 체인의 길이 정보를 설명하기 위해 생존 분석의 변형을 사용하여 평균 분리 정도를 추정할 ^[9]때 편향을 감소시킨다.
2. Milgram의 방법론의 주요 특징 중 하나는 참가자들이 대상 개인을 알 가능성이 가장 높은 사람을 선택하도록 요구받는 것입니다.그러나 많은 경우, 참가자들은 그들의 친구들 중 누가 대상을 가장 잘 알고 있는지 확신할 수 없을 것이다.따라서, 밀그램 실험 참가자들은 소셜 네트워크의 위상 지도를 가지고 있지 않기 때문에, 그들은 실제로 패키지를 최단 경로를 따라 보내기 보다는 타깃으로부터 더 멀리 보내고 있을 수 있다.이로 인해 루트 길이가 증가하여 랜덤한 2명의 접속에 필요한 평균 연결 수가 과대평가될 가능성이 매우 높아집니다.국가의 완전한 소셜 그래프에 접근할 수 있는 전지적 경로 계획자는 일반적으로 국지적 결정만을 내리는 탐욕 알고리즘에 의해 생성된 경로보다 짧은 최단 경로를 선택할 수 있다.
3. 이질적인 소셜 네트워크에 대한 설명은 여전히 미해결의 의문으로 남아 있다.비록 몇 년 동안 많은 연구가 이루어지지 않았지만, 1998년 던컨 왓츠와 스티븐 스트로가츠는 네이처 저널에 획기적인 논문을 발표했다.마크 뷰캐넌은 "그들의 논문은 많은 과학 분야에 걸친 추가 연구의 폭풍을 촉발시켰다"고 말했다.Watts의 6도 책을 참조하십시오. 연결된 시대의 과학
4. Sentinelese와 같은 일부 커뮤니티는 완전히 고립되어 있으며, 그렇지 않으면 글로벌 체인을 방해합니다.일단 이 사람들이 발견되면, 그들은 세계와 경제적, 가족적, 또는 사회적 접촉이 거의 없기 때문에 세계의 대부분과 더 멀리 떨어져 있게 된다; 그들이 발견되기 전에, 그들은 다른 인구들과 어떤 정도도 떨어져 있지 않다.그러나 이러한 모집단은 항상 작기 때문에 통계적으로 유의성이 낮다.

이러한 방법론적인 비판 외에 개념적인 문제도 논의됩니다.분리 정도가 다른 간접 접촉 체인의 사회적 관련성을 고려한다.많은 공식적이고 경험적인 연구는 확산 과정에 초점을 맞추고 있지만, 작은 세계의 문제에 대한 문헌은 또한 종종 시작자가 목표 인물로부터 어떤 종류의 자원(예를 들어, 정보)을 얻으려고 하는 (밀그램의 실험과 유사)의 예를 사용하여 연구의 관련성을 설명한다.대상자에게 도달하기 위한 중개자 수.그러나 약 6도 길이의 간접 채널이 실제로 이러한 직접 검색에 사용되거나 이러한 검색 프로세스가 다른 수단(예:^[10] 디렉토리에서 정보를 찾는 것)에 비해 더 효율적이라는 것을 보여주는 경험적 연구는 거의 없다.

영향을 주다

사회과학

말콤 글래드웰의 티핑 포인트는 원래 ^[11]뉴요커지에 실린 기사를 바탕으로 "터널링" 개념에 대해 자세히 설명하고 있다.글래드웰은 사회학적 연구를 압축하는데, 6도 현상은 큰 연락망과 친구 네트워크를 가진 소수의 특별한 사람들("커넥터")에 의존한다고 주장한다.이러한 허브들은 약하게 연결된 대부분의 사람들 사이의 연결을 중개한다.

그러나 질병 전염에 대한 작은 세계 현상의 영향에 대한 최근 연구는 전반적으로 소셜 네트워크의 강한 연결 특성 때문에 인구에서 이러한 허브를 제거하는 것이 보통 그래프를 통한 평균 경로 길이에 거의 영향을 미치지 않는다는 것을 보여준다(Barrett et al., 2005).^{[citation needed]}

수학자와 배우

수학자나 배우와 같은 소규모 커뮤니티는 개인 또는 직업적 연대의 사슬에 의해 밀접하게 연결되어 있는 것으로 밝혀졌습니다.수학자들은 공통의 출판물을 바탕으로 폴 에르다스와의 거리를 설명하기 위해 에르다스 숫자를 만들었습니다.배우 케빈 베이컨과 그와 함께 영화에 출연한 다른 배우들에게도 비슷한 운동이 수행되었는데, 후자는 게임 "Six Degrees of Kevin Bacon"을 알리는 노력을 기울였다.배우-수학자-수학자-연기자를 위한 Erdds-Bacon의 합성번호도 있다.인기 있는 아시안 게임 바둑의 선수들은 그들이 가지고 ^[12]있는 경기를 통해 분리 정도를 계산하는 슈사쿠 숫자를 세어 위대한 선수 호닌보 슈사쿠와의 거리를 묘사한다.

소규모 문제에 대한 최신 연구

이 작은 세계의 질문은 오늘날에도 여전히 인기 있는 연구 주제이며, 여전히 많은 실험이 진행 중이다.예를 들어 Peter Dodds, Roby Muhamad 및 Duncan Watts는 전 세계 24,^[13]163개의 이메일 체인과 18개의 타깃이 참여한 밀그램의 실험을 처음으로 대규모로 복제했습니다.

도즈 외 연구진도 평균 체인 길이가 약 6인 것을 발견했다.카네기 멜론 대학에서도 인기 있는 소셜 네트워킹 사이트를 매개로 한 유사한 실험이 실시되었다.그 결과, 실제로 수신처에 도달한 메시지는 극히 적었습니다.그러나 밀그램의 실험에 적용되는 비판은 현재 ^{[citation needed]}연구에도 크게 적용된다.

네트워크 모델

1998년, 코넬 대학의 Duncan J. Watts와 Steven Strogatz는 작은 세계 현상에 대한 최초의 네트워크 모델을 발표했습니다.그들은 전력망과 C. elegans의 신경망과 같은 자연계와 인공계의 네트워크가 작은 세계 현상을 나타낸다는 것을 보여주었다.Watts와 Strogatz는 규칙적인 격자에서 시작하여 소수의 랜덤 링크를 추가하면 네트워크 내의 두 꼭지점 사이의 가장 긴 직접 경로인 직경이 매우 긴 것에서 매우 짧은 것으로 감소한다는 것을 보여주었습니다.이 연구는 원래 곤충들이 보이지 않는 전도체에 의해 인도되는 것처럼 긴 범위에 걸쳐 높은 수준의 협응을 보여주는 크리켓의 울음소리를 이해하려는 와츠의 노력에서 영감을 받았다.왓츠와 스트로가츠가 이 현상을 설명하기 위해 개발한 수학적 모델은 이후 다양한 분야에 적용되어 왔다.Watts의 표현:^[14]

영문학 이외의 모든 분야에서 연락을 받은 것 같습니다.저는 수학자, 물리학자, 생화학자들, 신경생리학자들, 역학자들, 경제학자, 사회학자들로부터 편지를 받았습니다. 마케팅, 정보 시스템, 토목 공학, 그리고 인터넷의 네트워킹 목적으로 작은 세계의 개념을 사용하는 기업들로부터요.

일반적으로, 그들의 모델은 소셜 네트워크를 결속시키는 것은 "약한 ^[15]유대의 힘"이라는 마크 그라노베터의 관찰에서 진실을 보여주었다.이후 Jon^{[citation needed]} Kleinberg에 의해 특정 모델이 일반화되었지만, 복잡한 네트워크 분야의 표준 사례 연구로 남아 있습니다.네트워크 이론에서, 작은 세계 네트워크 모델에서 제시된 아이디어는 상당히 광범위하게 탐구되어 왔다.실제로 랜덤 그래프 이론의 몇 가지 고전적인 결과는 실제 위상 구조가 없는 네트워크에서도 작은 세계 현상이 나타난다는 것을 보여준다.이것은 수학적으로 (격자의 경우와 같이 노드 수에 비례하는 것이 아니라) 노드 수의 로그와 함께 성장하는 네트워크의 직경으로 표현된다.이 결과도 마찬가지로 스케일프리 네트워크 등의 멱함수 분포가 있는 네트워크에 매핑됩니다.

컴퓨터 과학에서 작은 세계 현상(일반적으로 그렇게 불리지 않지만)은 안전한 피어 투 피어 프로토콜, 인터넷과 애드혹 무선 네트워크를 위한 새로운 라우팅 알고리즘 및 모든 종류의 통신 네트워크를 위한 검색 알고리즘 개발에 사용됩니다.

대중문화에서

소셜 네트워크는 미국과 다른 지역의 대중문화에 널리 퍼졌다.특히 6도라는 개념은 집단 의식의 일부가 되었다.페이스북, 링크드인, 인스타그램 등 소셜네트워크서비스(SNS)는 소셜네트워크 개념을 적용해 온라인 공간의 연결성을 크게 높였다.

「 」를 참조해 주세요.

• 베이컨 수
• 던바의 수 – 사회학 및 인류학에서 중요한 인지 한계 제안
• Erd's 숫자 – 수학자 Paul Erd's와의 연관성 근접성
• Erdbs – Bacon 수 – 수학자 Paul Erd mathems 및 배우 Kevin Bacon과의 친밀감
• 퍼스널 네트워크
• 랜덤 워크 – 일련의 랜덤 스텝으로 구성된 경로의 수학적 공식화
• 랜덤 그래프 – 랜덤 프로세스에 의해 생성된 그래프
• 리처드 길리엄 – 미국 작가

레퍼런스

외부 링크

• 인스턴트 메시징 네트워크상의 행성 규모 뷰
• 특정 그룹에 대해 테스트된 이론:
  • 버지니아에 있는 베이컨의 신탁
  • 야구계의 오라클
  • Erd's Number 프로젝트
  • 오라클 오브 뮤직
  • CoverTrek - 커버 버전을 통해 밴드와 뮤지션 연결
  • 과학의 금요일:허블/소세계 네트워크의 미래
  • "Knock, Knock, Knocking on Newton's Door" (PDF). Archived from the original (PDF) on 2009-08-24. (223 KiB) – 방위사업대학지 Defense AT&L에 '작은 세계/큰 텐트' 소셜 네트워킹 모델을 제안하는 기고