체인 콤플렉스

수학에서 체인 콤플렉스(chain complex)는 아벨 그룹(또는 모듈)의 순서와 각 동형성의 이미지가 다음 그룹의 커널에 포함되도록 연속된 그룹 사이의 동형성의 순서로 구성된 대수적 구조다.체인 콤플렉스와 연관된 것은 이미지가 커널에 어떻게 포함되는지를 설명하는 그것의 호몰로지다.

코체인 콤플렉스는 동형성이 반대 방향에 있다는 점을 제외하면 체인 콤플렉스와 비슷하다.코체인 콤플렉스의 호몰로지(homology)는 코호몰로지(cohomology)라고 불린다.

대수적 위상에서는 위상학적 공간 X의 단일한 체인 콤플렉스는 심플렉스부터 엑스까지의 연속적인 지도를 이용하여 구성되며, 체인 콤플렉스의 동음질들은 이러한 맵들이 심플렉스 경계까지 어떻게 제한하는지 포착한다.이 체인 콤플렉스의 호몰로지(homology)는 X의 단일한 호몰로지(homology)라고 불리며, 위상학 공간의 불변성(不同性)으로 통용된다.

체인 콤플렉스는 호몰로지 대수학에서 연구되지만 추상 대수학, 갈루아 이론, 미분 기하학, 대수 기하학 등 수학의 여러 분야에서 사용된다.그것들은 아벨의 범주에서 더 일반적으로 정의될 수 있다.

정의들

체인 콤플렉스 $A$ $(A_{\bullet },d_{\bullet })$ , d $(A_{\bullet },d_{\bullet })$ ) ${\displaystyle (A_$ {\bullet $}}}}$ 는 아벨리아 그룹 또는 모듈 ..., A₀, A₁, A, A, A₂, A, A₃, ...(경계 연산자 또는_n 차등이라 함) d : A_n → A₄, ...로 연결된_n−1 일련의 것으로서 $(A_{\bullet },d_{\bullet })$ , 어떤 연속된 2개의 지도 구성이 0이 된다.분명히 차등분들은 d_n ∘ d_n+1 = 0을 만족시키거나, 또는 지수를 억제한 상태에서² d = 0을 만족시킨다.단지는 다음과 같이 기재할 수 있다.

\cdots {\x왼쪽 화살표 {d_{0}}A_{0}{\xleftarrow {d_{1}:{1}A_{1}{\xleftarrow {d_{2}}:}{\xleftarrow {d_{3}}A_{3}}{\xleftarrow {d_{4}}}{4}}}{xleftarrow}cd}cd}}}cd}}cd}}cd}cd}cd}}}cd}cd}}cd}cd}cdots}}}}}}cd}

코체인 콤플렉스 $(A^{\bullet },d^{\bullet })$ $(A^{\bullet },d^{\bullet })$ , $(A^{\bullet },d^{\bullet })$ $(A^{\bullet },d^{\bullet })$ ) ${\displaystyle (A^{\bullet },d^{\bullet }})$ 는 체인 콤플렉스에 대한 이중 개념이다 $(A^{\bullet },d^{\bullet })$ .아벨 그룹이나 모듈들의 시퀀스⁰, A¹, A², A³, A⁴, A, ... 동형문자 dⁿ : A → Aⁿ⁺¹ 만족ⁿⁿ⁺¹ dⁿ = 0으로 연결된다.코체인 콤플렉스는 체인 콤플렉스와 유사한 방식으로 작성될 수 있다.

\cdots {\xrightarrow {d^{-1}}A^{0}{\x오른쪽 화살표 {d^{0}}A^{1}{\x오른쪽 화살표 {d^{1}}A^{2}{\x오른쪽 화살표 {d^{2}}:}A^{3}{\x오른쪽 화살표 {d^{3}}A^{4}{\x오른쪽 화살표 {d^{4}}\cdots }

A_n 또는 A의ⁿ 지수 n을 도(또는 치수)라고 한다.체인단지와 코체인단지의 차이는 체인단지의 경우 차원이 줄어드는 반면, 코체인단지의 경우 차원이 늘어난다는 점이다.체인 단지에 대한 모든 개념과 정의는 코체인 단지에 적용되며, 차원에 대한 이러한 상이한 관례를 따를 것이라는 점을 제외하고, 코체인 단지에 적용되며, 용어에는 종종 공동이라는 접두어가 붙는다.본 기사에서는 구분이 필요하지 않을 때 체인 단지에 대한 정의를 제시한다.

경계 체인 단지는 거의 모든 A가_n 0인 것, 즉 0에 의해 좌우로 확장되는 유한 단지를 말한다.유한한 단순화단지의 단순화 동질성을 정의하는 연쇄단지가 그 예다.체인 콤플렉스는 일부 고정도 N 이상의 모든 모듈이 0일 경우 위로 경계되고, 일부 고정도 이하의 모든 모듈이 0일 경우 아래로 경계된다.분명히 콤플렉스는 콤플렉스를 경계하는 경우에만 위아래로 경계한다.

a 체인 단지의 개별 그룹의 요소를 (코)체인이라고 한다.d의 커널에 있는 원소를 (co)주기(또는 닫힌 원소)라고 하고, d의 영상에 있는 원소를 (co)경계(또는 정확한 원소)라고 한다.미분 정의에서 바로, 모든 경계는 사이클이다.n번째(co)호몰로지 그룹 H_n(Hⁿ)는 (co)cycle modulo(co) boundaries의 그룹이다. 즉, n번째(co)h(co)h(co)cycle modulo(co) boundaries의 그룹이다.

{\dplaystyle H_{n}=\ker d_{n}/{\mbox{{d_{n+1}}\quad \left(H^{n}=\ker d^{n}/{\mbox{}}}{{d^{n-1}\오른쪽)}}}}

정확한 순서

정확한 수열(또는 정확한 복합체)은 호몰로지 집단이 모두 0인 연쇄 복합체다.이는 단지 내 모든 폐쇄적 요소가 정확하다는 것을 의미한다.정확한 짧은 순서는 A_k, A_k+1, A_k+2 그룹만 0이 아닐 수 있는 경계된 정확한 순서다.예를 들어, 다음의 체인 콤플렉스는 짧은 정확한 시퀀스다.

\cdots {\xrightarrow {}}\;0\;{\xrightarrow {}}\;\mathbf {Z} \;{\xrightarrow {\times p}}\;\mathbf {Z} \twoheadrightarrow \mathbf {Z} /p\mathbf {Z} \;{\xrightarrow {}}\;0\;{\xrightarrow {}}\cdots

중간 그룹에서 닫힌 요소는 원소 pZ이다; 이것들은 분명히 이 그룹에서 정확한 원소들이다.

체인 맵

A chain map f between two chain complexes $(A_{\bullet },d_{A,\bullet })$ and $(B_{\bullet },d_{B,\bullet })$ is a sequence $f_{\bullet }$ of homomorphisms ${\displaystyle f_{n}:$ $A_{n}\rightarrow B_{n}}$ for each n that commutes with the boundary operators on the two chain complexes, so $d_{B,n}\circ f_{n}=f_{n-1}\circ d_{A,n}$ . This is written out in the following commutative diagram.

체인 맵은 사이클과 경계의 주기를 경계로 보내며, 따라서 $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ f $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ ) ( $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ , $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ ) $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ → $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ ( $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ , $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$ , $){\displaystyle (f_{\bullet }}_{*}):$ $H_{\bullet }(A_{\bullet },d_{A,\bullet })\오른쪽$ 화살표 $H_{\bullet }(B_{\bullet },d_{B,\bullet$ $(f_{\bullet })_{*}:H_{\bullet }(A_{\bullet },d_{A,\bullet })\rightarrow H_{\bullet }(B_{\bullet },d_{B,\bullet })$

위상학 공간인 X와 Y 사이의 연속 지도 f는 X와 Y의 단수 체인 콤플렉스 사이에 체인 맵을 유도하고, 따라서 X와 Y의 단수 호몰로지 사이에도 맵 f를_* 유도한다.X와 Y가 모두 n-sphere와 같을 때, 동질학에서 유도된 지도는 지도 f의 정도를 정의한다.

체인 맵의 개념은 체인 맵의 원뿔 구성을 통해 경계 중 하나로 줄어든다.

체인 호모토피

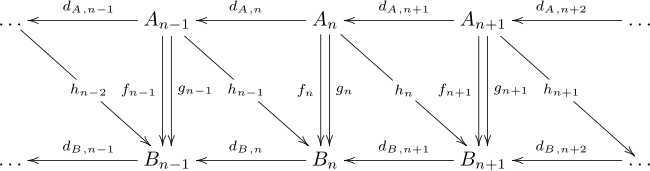
체인 호모토피(chain homotopy)는 비록 지도가 다를 수 있지만, 호몰로지 그룹에서 동일한 지도를 유도하는 두 개의 체인 맵을 연관시키는 방법을 제공한다.체인 호모토피는 A와 B의 두 개의 체인 콤플렉스와 f의 두 개의 체인 맵을 볼 때 hd_A + dh_B = f - g와 같은 동형체 h_n : A_n → B의_n+1 연속이다.지도는 다음과 같이 도표로 작성할 수 있으나, 이 도표는 서로 일치하지 않는다.

지도 hd_A + dh는_B h에 대해 동질학 제로 지도를 유도하기 위해 쉽게 검증된다.그것은 즉시 f와 g가 동음이의학에서 같은 지도를 유도한다는 것을 따른다.하나는 f와 g가 체인 동음이의학(또는 단순히 동음이의학)이며, 이 속성은 체인 맵 사이의 동등성 관계를 정의한다고 말한다.

X와 Y는 위상학적 공간이 되게 하라.단수 호몰로학의 경우, 연속 지도 f, g : X → Y 사이의 호모토피는 f와 g에 해당하는 체인 지도 사이에 체인 호모토피를 유도한다.이것은 두 개의 동음이의어 지도가 단일 동음이의학에서 동일한 지도를 유도한다는 것을 보여준다.체인 호모토피(chain homotophy)라는 명칭은 이 예에서 동기를 부여받은 것이다.

예

단수 호몰로지

X를 위상학적 공간이 되게 하라.자연 n이 X의 단수 n-심플라이스에 의해 공식적으로 생성된 자유 아벨리아 그룹이 되도록 C_n( $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ )를 정의하고 경계 지도 $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ map n : C $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ ) $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ → $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ - $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ ( $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ ) ${\displaystyle \partial _{n}:$ $C_{n}(X)\to C_{n-1}(X)}$ 이 $\partial _{n}:C_{n}(X)\to C_{n-1}(X)$ (가) 될 대상

\partial _{n}:\,(\sigma :[v_{0},\ldots ,v_{n}]\to X)\mapsto (\sum _{i=0}^{n}(-1)^{i}\sigma :[v_{0},\ldots ,{\hat {v}}_{i},\ldots ,v_{n}]\to X)

모자가 꼭지점 누락을 나타내는 곳즉, 단일 심플렉스(simplex)의 경계는 그 면에 대한 제약의 교차합이다.∂² = 0이므로 $(C_{\bullet },\partial _{\bullet })$ ( $(C_{\bullet },\partial _{\bullet })$ $(C_{\bullet },\partial _{\bullet })$ , $(C_{\bullet },\partial _{\bullet })$ $(C_{\bullet },\partial _{\bullet })$ ) ${\displaystyle (C_{\bullet }},\partial _{\bullet }}}})$ 은 체인 $(C_{\bullet },\partial _{\bullet })$ 콤플렉스임을 알 수 있다. 단수 $H_{\bullet }(X)$ H $H_{\bullet }(X)$ ( $H_{\bullet }(X)$ ) ${\displaystyle$ H_ ${\bullet }(X)$ 는 $H_{\bullet }(X)$ 이 콤플렉스의 호몰로지이다.

특이 동질학은 호모토피 균등성까지의 위상학적 공간의 유용한 불변성이다.학위 제로 호몰로지 그룹은 X의 경로 구성 요소에서 자유로운 아벨리아 그룹이다.

드 람 코호몰로지

매끄러운 다지관 M에 있는 미분 k-폼은 추가 시 Ω^k(M)이라는 실제 벡터 공간을 형성한다.외부² 파생상품 d맵 Ω^k(M)에서 Ω^k+1(M)까지, d = 0은 기본적으로 두 번째 파생상품의 대칭에서 따르기 때문에 외부 파생상품과 함께 k-폼의 벡터 공간은 코체인 복합체다.

\Oomega ^{0}(M)\\\stackrel {d}{\}}}\\Oomega ^{1}(M)\Oomega ^{2}(M)\to \Oomega ^{3}(M)\codots }}}

이 콤플렉스의 코호몰로지(cohomology)는 X의 데 람 코호몰로지(de Rham cohomology)라고 불린다.치수 0의 호몰로지 그룹은 M에서 R까지의 국소 상수 함수의 벡터 공간에 이형성이다.따라서 콤팩트 매니폴드의 경우, 이것은 M의 연결된 구성 요소의 수인 실제 벡터 공간이다.

다지관 사이의 매끄러운 지도는 체인 맵을 유도하고, 지도 사이의 매끄러운 호모토피들은 체인 호모토피를 유도한다.

체인단지의 분류

체인 맵을 가진 K-module의 체인 콤플렉스는 범주 Ch를_K 형성하며, 여기서 K는 상호 작용 링이다.

V ${}_{*}$ = V ${}_{*}$ ${\$ W = W ${}_{*}$ { ${}_{*}$ {\ $displaystyle {}{*}}$ 이 ${}_{*}$ 체인 복합체라면 텐서 $V\otimes W$ V $V\otimes W$ { $V\otimes W$ {\ $displaystyle$ V\ $otimes$ W $}$ 은(는)에 의해 n개의 요소가 주어지는 체인 복합체다 $V\otimes W$ .

(V\otimes W)_{n}=\bigoplus _{\\i,j i+j=n\}}{V_{i}\otimes W_{j}}

그리고 다음이 주는 차이점

\displaystyle \cHB=\display a\otimes b+(-1)^{\\좌측 a\a\otimes \otimes b}

여기서 a와 b는 각각 V와 W에서 두 개의 동일한 벡터로서, ${\$ a $\오른쪽 }$ 은 a의 정도를 나타낸다 $\left|a\right|$ .

이 텐서 제품은 Ch_K 범주를 대칭 단면체 범주로 만든다.이 모노이드 제품에 관한 ID 객체는 도 0의 체인 콤플렉스로 보이는 베이스 링 K이다.브레이딩은 동질 원소의 단순한 텐더에 의해 주어진다.

a\otimes b\mapsto(-1)^{\\\좌우 \좌우 \좌우 \b\otimes a}

그 표지판은 브레이딩이 체인 맵이 되려면 필요하다.

더욱이 K-modules의 체인 콤플렉스 범주에도 내부 Hom이 있다: 주어진 체인 콤플렉스 V와 W의 내부 Hom(V,W)으로 표기된 $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ (V,W)은 $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ i $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ K $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ , $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ + n $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ ${\displaysty \Pi _{i}\text$ }{\cext $}$ 가 부여한 등급 n의 체인 콤플렉스다. $홈}_{K}(V_{i},W_{i+n})$ 및 차동 $\Pi _{i}{\text{Hom}}_{K}(V_{i},W_{i+n})$ 제공자

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

)

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

) =

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

(

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

)

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

-

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

(

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

- 1

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

)

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

(

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

f (

(\partial f)(v)=\partial (f(v))-(-1)^{\left|f\right|}f(\partial (v))

f ( )

{\displaystyle (\partialf)(v)=\

displaystyle (\display f)=\

f(v)-(-1)^{\좌측

f

\f(\f

우리는 자연적인 이형성을 가지고 있다.

{\text{홈}(A\otimes B,C)\cong {\text{홈}(A,{\text{홈}(B,C)

추가 예

참고 항목

차등등급대수학
차등등급 리 대수
돌드칸 통신사는 체인단지의 범주와 단순한 아벨 그룹의 범주가 동등하다고 말한다.
Buchsbaum-Eisenbud acycyclicity 기준
차등 등급 모듈

참조

^ https://ncatlab.org/nlab/show/graph+complex

Bott, Raoul; Tu, Loring W. (1982), Differential Forms in Algebraic Topology, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90613-3
Hatcher, Allen (2002). Algebraic Topology. Cambridge: Cambridge University Press. ISBN 0-521-79540-0.

[1] ttps://ncatlab.org/nlab/show/graph+complex

[1]

Search