횡압 작용에 의한 가장자리 클램핑 원형 판의 휨. 판의 왼쪽 반쪽은 기형적인 모양을, 오른쪽 반쪽은 비정형 형태를 보여준다. 이 계산은 앤시스 를 사용하여 수행되었다. 판의 휨, 즉 판의 휨 은 외부 힘 과 모멘트 의 작용에 따라 판의 평면에 수직으로 판이 편향 되는 것을 말한다. 편향의 양은 적절한 판 이론 의 미분 방정식을 풀어서 결정할 수 있다. 플레이트의 응력 은 이러한 편향으로 계산할 수 있다. 일단 스트레스가 알려지면, 고장 이론 을 사용하여 주어진 부하에서 플레이트가 고장날지 여부를 판단할 수 있다.
Kirchhoff-Love 판의 휨 정의들 두께 H {\displaystyle H 영의 계량 E {\displaystyle E} 포아송의 비율 ν {\displaystyle \nu} w {\\displaystyle w}) .
휨 강성 은 다음에 의해 주어진다.
D = E H 3 12 ( 1 − ν 2 ) {\displaystyle D={\frac {EH^{3}}{12\왼쪽(1-\nu ^{2}\오른쪽) }}} 순간 단위 길이당 벤딩 모멘트 는 다음과 같이 주어진다.
M x = − D ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) {\displaystyle M_{x}=-D\왼쪽({\frac {\partial ^{2}w}{\partial x^{2}}+}\nu {\frac {\partial ^{2}w}{\partial y^{2}}}\오른쪽)}}} M y = − D ( ν ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 ) {\displaystyle M_{y}=-D\left(\nu {\frac {\partial ^{2}w}{2}}+{\partial ^{2}w}{\partial y^{2}}}\오른쪽)}}} 단위 길이당 비틀림 모멘트 는 다음과 같다.
M x y = − D ( 1 − ν ) ∂ 2 w ∂ x ∂ y {\displaystyle M_{xy}=-D\왼쪽(1-\nu \오른쪽){\frac {\partial ^{2}w}{\partial x\partial y}}} 폭력 단위 길이당 전단력 은 다음과 같이 주어진다.
Q x = − D ∂ ∂ x ( ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 ) {\displaystyle Q_{x}=-D{\frac {\partial x}}{\partial x}{2}w}{\partial x^{2}}+{\partial y^{2}w}{\partial y^{2}}\partial y^{2}}\오른쪽)}}} Q y = − D ∂ ∂ y ( ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 ) {\displaystyle Q_{y}=-D{\frac {\partial y}{\partial y}{2}w}{\partial x^{2}}+{\partial y^{2}w}{\partial y^{2}}}\partial y^{2}}\오른쪽)}} 스트레스 벤딩 응력 은 다음에 의해 주어진다.
σ x = − 12 D z H 3 ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) {\displaystyle \sigma _{x}=-{\frac {12Dz}{ H^{3}}}\왼쪽({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu {\partial ^{2}w}{\partial y^{2}}}\오른쪽)}}} σ y = − 12 D z H 3 ( ν ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 ) {\displaystyle \sigma _{y}=-{\frac {12Dz}{ H^{3}}}\왼쪽(\nu {\frac {\partial ^{2}w}{\partial x^{2}}+{\partial ^{2}w}{\partial y^{2}}}\오른쪽)}}} 전단 응력 은 다음에 의해 주어진다.
τ x y = − 12 D z H 3 ( 1 − ν ) ∂ 2 w ∂ x ∂ y {\displaystyle \tau _{xy}=-{\frac {12Dz}{ H^{3}}}\왼쪽(1-\nu \오른쪽){\frac {\partial ^{2}w}{\partial x\partial y}}}} 균주 소편향 이론에 대한 벤딩 스트레인 은 다음과 같다.
ϵ x = ∂ u ∂ x = − z ∂ 2 w ∂ x 2 {\displaystyle \epsilon _{x}={\frac {\properties u}{\prac x}}=-z{\frac {\fract ^{2}w}{\propert x^{2}}: ϵ y = ∂ v ∂ y = − z ∂ 2 w ∂ y 2 {\displaystyle \epsilon _{y}={\frac {\fract v}{\fract y}}=-z{\fract {\fract ^{2}w}{\reason y^{2}}: 소편향 이론에 대한 전단 변형률 은 다음과 같다.
γ x y = ∂ u ∂ y + ∂ v ∂ x = − 2 z ∂ 2 w ∂ x ∂ y {\displaystyle \property}={xy}={\frace u}{\property y}+{\fract v}{\pract v}}=-2z={\fract ^{2}w}{\fract x\propers y}}}}}}}}}}}}} 대편향 판 이론의 경우, 막 변종의 포함을 고려한다.
ϵ x = ∂ u ∂ x + 1 2 ( ∂ w ∂ x ) 2 {\displaystyle \epsilon _{x}={\frac {\frac u}{\properties x}+{1}{1}{1}:{1}{prefac {1}{{\precipal x}\right)^{2}}: ϵ y = ∂ v ∂ y + 1 2 ( ∂ w ∂ y ) 2 {\displaystyle \epsilon _{y}={\frac {\fract v}{\precent y}+{1}{1}{1}{1}{{precent w}{\precipal y}\right)^{2}} γ x y = ∂ u ∂ y + ∂ v ∂ x + ∂ w ∂ x ∂ w ∂ y {\displaystyle \cHB}={\frac {\frace u}{\frace y}+{\frace v}{\fract x}+{\fract w}{\fract x}}{\fract w}{\fract w}{\fract w}{\frace w}{\frace y}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 편향 편향 은 에 의해 주어진다.
u = − z ∂ w ∂ x {\displaystyle u=-z{\frac {\reason w}{\reason x}}} v = − z ∂ w ∂ y {\displaystyle v=-z{\frac {\reason w}{\reason y}} 파생 판 에 대한 Kirchhoff-Love plate 이론 에서 지배 방정식은 다음과[1]
N α β , α = 0 {\displaystyle N_{\alpha \beta ,\alpha }=0} 그리고
M α β , α β − q = 0 {\displaystyle M_{\alpha \beta ,\alpha \beta }-q=0} 확장된 형태로,
∂ N 11 ∂ x 1 + ∂ N 21 ∂ x 2 = 0 ; ∂ N 12 ∂ x 1 + ∂ N 22 ∂ x 2 = 0 {\displaystyle {\cfrac {\partial N_{11}}{\partial x_{1}}}+{\cfrac {\partial N_{21}}{\partial x_{2}}}=0~;~~{\cfrac {\partial N_{12}}{\partial x_{1}}}+{\cfrac {\partial N_{22}}{\partial x_{2}}}=0} 그리고
∂ 2 M 11 ∂ x 1 2 + 2 ∂ 2 M 12 ∂ x 1 ∂ x 2 + ∂ 2 M 22 ∂ x 2 2 = q {\displaystyle {\cfrac {\partial ^{2}M_{11}}{\partial x_{1}^{2}}}+2{\cfrac {\partial ^{2}M_{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}M_{22}}{\partial x_{2}^{2}}}=q} 여기서 q ){\displaystyle q(x)} 하중 을 가한 것이며두께 2시간 {\displaystyle H=2h} , σ i j {\ displaystyle \sigma _{ij}} ,
N α β := ∫ − h h σ α β d x 3 ; M α β := ∫ − h h x 3 σ α β d x 3 . {\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}~.} 수량 N {\displaystyle N} 힘 의 단위가 있다 수량 M {\displaystyle M} 모멘트 단위가 있다
등방성 , 균일성 의 경우영의 계량 {\displaystyle E} 포아송 의 비율 ν {\displaystyle \nu} [2]
∇ 2 ∇ 2 w = − q D ; D := 2 h 3 E 3 ( 1 − ν 2 ) = H 3 E 12 ( 1 − ν 2 ) {\displaystyle \nabla ^{2}\nabla ^{2}w=-{\cfrac {q}{D}}~~D: ={\cfrac {2h^{3}E}{3}{3}}{{3}}}}}}={\cfrac {H^{3}E}{12(1-\nu ^{2}}}}}}}}}}}}}}} 여기서 w x x 2 {\displaystyle w(x_{1},x_{2})
얇은 직사각형 판의 작은 편향 이는 제르맹-라그랑주 판 방정식에 의해 관리된다.
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = q D {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}} 이 방정식은 1811년 12월 라그랑주(Lagrange)가 이론의 기초를 제공한 저메인의 작품을 교정하는 과정에서 처음 도출한 것이다.
얇은 직사각형 판의 큰 편향 이것은 Föppl-von Karrman 판 방정식 에 의해 관리된다.
∂ 4 F ∂ x 4 + 2 ∂ 4 F ∂ x 2 ∂ y 2 + ∂ 4 F ∂ y 4 = E [ ( ∂ 2 w ∂ x ∂ y ) 2 − ∂ 2 w ∂ x 2 ∂ 2 w ∂ y 2 ] {\displaystyle {\displayac {\respect ^{4} }{{\partial x^{4}}+2{\cfrac {\partial ^{4}}{4} }F}{\partial x^{2}\partial y^{2}}+{\cfrac {\partial ^{4} }F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]} ∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = q D + H D ( ∂ 2 F ∂ y 2 ∂ 2 w ∂ x 2 + ∂ 2 F ∂ x 2 ∂ 2 w ∂ y 2 − 2 ∂ 2 F ∂ x ∂ y ∂ 2 w ∂ x ∂ y ) {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {q}{D}}+{\cfrac {H}{D}}\left({\cfrac {\partial ^{2}F}{\partial y^{2}}}{\cfrac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {\partial ^{2}F}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}:2}}-{\cfrac {\partial ^{2}F}{\partial x\partial y}{\partial ^{2}w}{\partial x\partial y}\오른쪽)}} 여기 {\displaystyle F}
원형 키르슈호프-러브 플레이트 원형 판의 휨은 적절한 경계조건으로 지배 방정식을 풀어서 조사할 수 있다. 이러한 해결책은 1829년 포아송에 의해 처음 발견되었다. 원통형 좌표는 이런 문제에 편리하다. 여기서 z {\displaystyle z}
좌표가 없는 형태의 지배 방정식은
∇ 2 ∇ 2 w = − q D . {\displaystyle \nabla ^{2}\nabla ^{2}w=-{\frac {q}{D}\, } 원통형 좌표(r θ {\displaystyle(r,\theta ,z
∇ 2 w ≡ 1 r ∂ ∂ r ( r ∂ w ∂ r ) + 1 r 2 ∂ 2 w ∂ θ 2 + ∂ 2 w ∂ z 2 . {\displaystyle \nabla ^{2}w\equiv {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial w}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}w}{\partial \theta ^{2}}}+{\frac {\partial ^{2}w}{\partial z^{2}}}\,. } 대칭으로 적재된 원형 플레이트의 경우 w w {\displaystyle w=w(r)} (
∇ 2 w ≡ 1 r d d r ( r d w d r ) . {\displaystyle \dr}{dr}{dr}\{dr}\좌측(r{\dr}{dr}{dr}\오른쪽)\, } 그러므로 지배 방정식은 다음과 같다.
1 r d d r [ r d d r { 1 r d d r ( r d w d r ) } ] = − q D . {\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,. } q {\displaystyle q} D {\displaystyle D}
w ( r ) = − q r 4 64 D + C 1 ln r + C 2 r 2 2 + C 3 r 2 4 ( 2 ln r − 1 ) + C 4 {\displaystyle w(r)=-{\frac {qr^{4}{64D}+C_{1}{1}\ln r+{cfrac {C_{2}r^{2}}}{{2}}+{\cfrac {C_{3}r^{2}}:{4}}}}}}{4}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 여기 i {\ displaystyle C_{i} 편향면의 기울기는
ϕ ( r ) = d w d r = − q r 3 16 D + C 1 r + C 2 r + C 3 r ln r . {\displaystyle \phi(r)={\cfrac {dw}{dr}=-{\frac {qr^{3}}+{16D}+{{1}}{{r}}+C_{2}r+C_{3}r\ln r\, } 원형 플레이트의 경우 편향과 편향 기울기 r [\displaystyle r=0} C1 [\displaystyle C_{1}=0} . 단, 오른쪽 0 {\ displaystyle c_{3} rn n r {\ displaystyle \n \} C 3 displaystyle r=0}
클램핑된 모서리 가장자리가 클램핑된 원형 플레이트의 경우 플레이트 w {\displaystyle w(a)=0} ϕ {\displaystyle \phi (a)=0} 반경 a {\displaysty a}). 이러한 경계 조건을 사용하여 우리는 얻을 수 있다.
w ( r ) = − q 64 D ( a 2 − r 2 ) 2 그리고 ϕ ( r ) = q r 16 D ( a 2 − r 2 ) . {\displaystyle w(r)=-{\frac {q}{64D}(a^{2}-r^{2})^{2}^{2}^{2}}^{2}\2}\2}\quad {\text{and}\\\qr}{16D}(r)={\frac {qr}}. } 플레이트의 평면 내 변위는
u r ( r ) = − z ϕ ( r ) 그리고 u θ ( r ) = 0 . {\displaystyle u_{r}(r)=-z\phi(r)\properties {\text{and}}\property u_{\theta }(r)=0\,.} 플레이트의 평면 내 변종은
ε r r = d u r d r = − q z 16 D ( a 2 − 3 r 2 ) , ε θ θ = u r r = − q z 16 D ( a 2 − r 2 ) , ε r θ = 0 . {\displaystyle \varepsilon _{rr}={\cfrac {du_{r}}{dr}}=-{\frac {qz}{16D}}(a^{2}-3r^{2})~,~~\varepsilon _{\theta \theta }={\frac {u_{r}}{r}}=-{\frac {qz}{16D}}(a^{2}-r^{2})~,~~\varepsilon _{r\theta }=0\,.} 플레이트의 평면 내 응력은
σ r r = E 1 − ν 2 [ ε r r + ν ε θ θ ] ; σ θ θ = E 1 − ν 2 [ ε θ θ + ν ε r r ] ; σ r θ = 0 . {\displaystyle \sigma _{rr}={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{rr}+\nu \varepsilon _{\theta \theta }\right]~;~~\sigma _{\theta \theta }={\frac {E}{1-\nu ^{2}}}\left[\varepsilon _{\theta \theta }+\nu \varepsilon _{rr}\right]~;~~\sigma _{r\theta }=0\,.} 두께가 2시간 {\displaystyle 2h} , D E h 3 3 ν 2 ] {\displaystyle =2Eh^{3}/[3(1-\nu ^{2})]
σ r r = − 3 q z 32 h 3 [ ( 1 + ν ) a 2 − ( 3 + ν ) r 2 ] σ θ θ = − 3 q z 32 h 3 [ ( 1 + ν ) a 2 − ( 1 + 3 ν ) r 2 ] σ r θ = 0 . {\displaystyle {\regated}\prox{3qz}-{rrr&=-{\frac {3qz}{32h^{3}}\왼쪽[(1+\nu )a^{2}-(3+\nu )r^{2}\right]\ \\theta _{\theta }&=-{\frac {3qz}{32h^{3}}\왼쪽[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]\ \\cHBMA _{r\theta }&=0\, \end{정렬}}} 결과물(베인딩 순간)은
M r r = − q 16 [ ( 1 + ν ) a 2 − ( 3 + ν ) r 2 ] ; M θ θ = − q 16 [ ( 1 + ν ) a 2 − ( 1 + 3 ν ) r 2 ] ; M r θ = 0 . {\displaystyle M_{rr}=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(3+\nu )r^{2}\right]~;~~M_{\theta \theta }=-{\frac {q}{16}}\left[(1+\nu )a^{2}-(1+3\nu )r^{2}\right]~;~~M_{r\theta }=0\,.} 최대 z h {\displaystyle z=h} r {\displaystyle r=a
σ r r z = h , r = a = 3 q a 2 16 h 2 = 3 q a 2 4 H 2 왼쪽. \sigma _{rr}\오른쪽 _{z=h,r=a}={\frac {3qa^{2}}:{16h^{2}}}={\frac {3qa^{2}}:{4} H^{2}}:}} 여기 := 2시간 {\displaystyle :=2h 판의 경계와 중심에서 휨 모멘트는
M r r r = a = q a 2 8 , M θ θ r = a = ν q a 2 8 , M r r r = 0 = M θ θ r = 0 = − ( 1 + ν ) q a 2 16 . 왼쪽. M_{rr}\오른쪽 _{r=a}={\frac {qa^{2}}:{8},~~\왼쪽. M_{\theta \}\오른쪽 _{r=a}={\frac {\nu qa^{2}}~{8},~~\왼쪽. M_{rr}\오른쪽 _{r=0}=\왼쪽. M_{\theta \}\오른쪽 _{r=0}=-{\frac {(1+\nu )qa^{2}}:{16}\, } 직사각형 커쇼프-러브 플레이트 단위 면적당q {\displaystyle q} 직사각형 판의 경우 1820년 나비에르는 판이 단순하게 지지되었을 때 변위와 응력을 찾아내는 간단한 방법을 도입하였다. 적용된 하중을 푸리에 구성요소의 관점에서 표현하고, 사인하중(단일 푸리에 구성요소)에 대한 해결책을 찾은 다음 푸리에 구성요소를 겹쳐서 임의하중에 대한 해결책을 얻는 것이 발상이었다.
정현하중 하중이 형식이라고 가정해 봅시다.
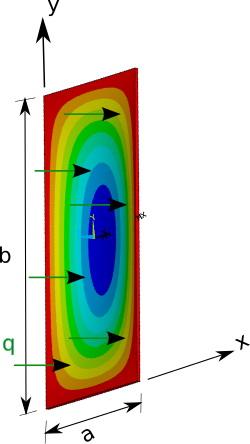
q ( x , y ) = q 0 죄를 짓다 π x a 죄를 짓다 π y b . {\displaystyle q(x,y)=q_{0}\sin {\frac {\pi x}{a}\sin {\frac {\pi y}{b}\, } 여기서 q 0 {\ displaystyle q_{0}} {\displaystyle a} ) x} {\displaystyle b} y {\displaysty y}
Since the plate is simply supported, the displacement w ( x , y ) {\displaystyle w(x,y)} M x x {\displaystyle M_{xx}} x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} M y y {\displaystyle M_{yy}} y = 0 {\ displaystyle y=0} y {\displaystyle y=b}
이러한 경계 조건을 적용하여 판 방정식을 풀면 해답이 나온다.
w ( x , y ) = q 0 π 4 D ( 1 a 2 + 1 b 2 ) − 2 죄를 짓다 π x a 죄를 짓다 π y b . {\displaystyle w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)^{-2}\,\sin {\frac {\pi x}{a}}\sin {\frac {\pi y}{b}}\,. } 여기서 D는 휨강성
D = E t 3 12 ( 1 − ν 2 ) {\displaystyle D={\frac {et^{3}}{12(1-\nu ^{2}}}}} 휨 강성 EI와 유사함.[3] 우리는 일단 변위를 알게 되면 판의 응력과 변형을 계산할 수 있다.
보다 일반적인 형태의 부하를 위해
q ( x , y ) = q 0 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle q(x,y)=q_{0}\sin {m\pi x}{a}\sin {\frac {n\pi y}{b}}}}} 여기 {\displaystyle m} n {\displaystyle n}
(1) w ( x , y ) = q 0 π 4 D ( m 2 a 2 + n 2 b 2 ) − 2 죄를 짓다 m π x a 죄를 짓다 n π y b . {\displaystyle {\text{(1)}}\qquad w(x,y)={\frac {q_{0}}{\pi ^{4}D}}\,\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{-2}\,\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,. } 나비에르 솔루션 이중 삼각계열 방정식 다음 양식의 일반q( x y {\displaystyle q(x,y)}
q ( x , y ) = ∑ m = 1 ∞ ∑ n = 1 ∞ a m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle q(x,y)=\sum _{m=1}^{\inflit }a_{mn}\sin {\m\pi x}{a}}\pin{b}}}}}}}} 여기 m n {\ displaystyle a_{mn}
a m n = 4 a b ∫ 0 b ∫ 0 a q ( x , y ) sin m π x a sin n π y b d x d y {\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{b}\int _{0}^{a}q(x,y)\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y} 따라서 작은 편향에 대한 고전적인 직사각형 판 방정식은 다음과 같이 된다.
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = 1 D ∑ m = 1 ∞ ∑ n = 1 ∞ a m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}+2{\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}w}{\partial y^{4}}}={\cfrac {1}{D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }a_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} 일반 하중을 받는 단순 지지 플레이트 다음 양식의w x y {\displaystyle w(x,y)}
w ( x , y ) = ∑ m = 1 ∞ ∑ n = 1 ∞ w m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle w(x,y)=\sum _{m=1}^{\inflat }{n1}^{n=1}{n=1}^{n1}^{n1}\flac {m\pi x}{a}}\pin{b}}}}}}}}}} 이 기능의 부분적인 차이는 다음과 같다.
∂ 4 w ∂ x 4 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( m π a ) 4 w m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} ∂ 4 w ∂ x 2 ∂ y 2 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( m π a ) 2 ( n π b ) 2 w m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {m\pi }{a}}\right)^{2}\left({\frac {n\pi }{b}}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} ∂ 4 w ∂ y 4 = ∑ m = 1 ∞ ∑ n = 1 ∞ ( n π b ) 4 w m n 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle {\cfrac {\partial ^{4}w}{\partial y^{4}}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left({\frac {n\pi }{b}}\right)^{4}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} 이 표현들을 판 방정식에 대입해 보면,
∑ m = 1 ∞ ∑ n = 1 ∞ ( ( m π a ) 2 + ( n π b ) 2 ) 2 w m n 죄를 짓다 m π x a 죄를 짓다 n π y b = ∑ m = 1 ∞ ∑ n = 1 ∞ a m n D 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }\left(\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}\right)^{2}w_{mn}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}=\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\cfrac {a_{mn}}{D}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} 두 가지 표현을 동일시하면, 우리는
( ( m π a ) 2 + ( n π b ) 2 ) 2 w m n = a m n D {\displaystyle \left(왼쪽({\frac {m\pi }{a}\오른쪽)^{2}+\{2}+\{{b}\오른쪽)^{2}w_{mn}={\cfrac {a_{mn}}{D}}}}}}}}}}}}}}}}}}}} 다시 배열해서 줄 수 있는
w m n = 1 π 4 D a m n ( m 2 a 2 + n 2 b 2 ) 2 {\displaystyle w_{mn}={\frac {1}{\pi ^{4}D}{\frac {a_{mn}}}{\frac {m^{2}}:}+{\frac{n^{n^{2}}}}}{b^{2}}:}\2}}:2}}:00}}}}}}}{{{{{{{{{{{2}}:}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 일반 하중을 받는 단순 지지 플레이트(코너-원점)의 편향은 다음과 같다.
w ( x , y ) = 1 π 4 D ∑ m = 1 ∞ ∑ n = 1 ∞ a m n ( m 2 a 2 + n 2 b 2 ) 2 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle w(x,y)={\frac {1}{\pi ^{4}D}}\sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {a_{mn}}{\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} 균일하게 분포된 하중을 가진 단순 지지 플레이트 변위(w {\displaystyle w} 스트레스(σ {\ displaystyle \sigma _{xx 스트레스 ( σ y {\ displaystyle \sigma _{y Displacement and stresses along x = a / 2 {\displaystyle x=a/2} a = 20 {\displaystyle a=20} b = 40 {\displaystyle b=40} H = 2 h = 0.4 {\displaystyle H=2h=0.4} E = 70 {\displaystyle E=70} ν = 0.35 {\displaystyle \nu =0.35} q 0 = − 10 [\displaystyle q_{0}=-10} 빨간색 선은 접시 바닥, 녹색 선은 가운데, 파란색 선은 접시 윗부분을 나타낸다. 균일하게 분산된 하중을 위해
q ( x , y ) = q 0 {\displaystyle q(x,y)=q_{0}} 따라서 해당 푸리에 계수는 다음과 같이 주어진다.
a m n = 4 a b ∫ 0 a ∫ 0 b q 0 sin m π x a sin n π y b d x d y {\displaystyle a_{mn}={\frac {4}{ab}}\int _{0}^{a}\int _{0}^{b}q_{0}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}\,{\text{d}}x{\text{d}}y} 이중 적분을 평가해 보면
a m n 4 q 0 π 2 m 1 cos m π 1 cos n π ){mn}={\frac {4q_{0}}{\pi ^{2}mn}}(1-\cos m\pi )}, 또는 조각 으로 된 포맷으로,
a m n = { 16 q 0 π 2 m n m 그리고 n 기묘한 0 m 또는 n 짝수 {\displaystyle a_{mn}={\case}{\pi ^{16q_{0}}{{2}mn}~{\text{and}}{\text{0&m~{\text{n}~{\text{n}~{\text{ven}}\case}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}? 균일하게 분배된 하중을 가진 단순 지지 플레이트(코너-원점)의 편향은 다음과 같다.
w ( x , y ) = 16 q 0 π 6 D ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ 1 m n ( m 2 a 2 + n 2 b 2 ) 2 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle w(x,y)={\frac {16q_{0}{\pi ^{6}D}\sum _{m=1,3,5,... }^{\put }\sum _{n=1,3,5,... }^{\inflit }{\frac {1}{mn\leftleft\frac{2}}:{a^{2}}:}+{n^{2}}:{b^{2}}:}}^{2}}:}}}}}}}}}}}}}}}}\신 {m\pi x}{a}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 플레이트의 단위 길이당 벤딩 모멘트는 다음과 같이 주어진다.
M x = 16 q 0 π 4 ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ m 2 a 2 + ν n 2 b 2 m n ( m 2 a 2 + n 2 b 2 ) 2 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle M_{x}={\frac {16q_{0}{\pi ^{4}}\sum _{m=1,3,5,... }^{\put }\sum _{n=1,3,5,... }^{\infty }{\frac {{\frac {m^{2}}{a^{2}}}+\nu {\frac {n^{2}}{b^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} M y = 16 q 0 π 4 ∑ m = 1 , 3 , 5 , . . . ∞ ∑ n = 1 , 3 , 5 , . . . ∞ n 2 b 2 + ν m 2 a 2 m n ( m 2 a 2 + n 2 b 2 ) 2 죄를 짓다 m π x a 죄를 짓다 n π y b {\displaystyle M_{y}={\frac {16q_{0}{\pi ^{4}}\sum _{m=1,3,5,... }^{\put }\sum _{n=1,3,5,... }^{\infty }{\frac {{\frac {n^{2}}{b^{2}}}+\nu {\frac {m^{2}}{a^{2}}}}{mn\left({\frac {m^{2}}{a^{2}}}+{\frac {n^{2}}{b^{2}}}\right)^{2}}}\sin {\frac {m\pi x}{a}}\sin {\frac {n\pi y}{b}}} 레비 용액 또 다른 접근법은 1899년 레비 에[4] 이 경우, 우리는 가정된 형태의 변위로부터 시작하여 지배 방정식과 경계 조건이 충족되도록 매개변수를 맞추려고 한다. The goal is to find Y m ( y ) {\displaystyle Y_{m}(y)} y = 0 {\displaystyle y=0} y = b {\displaystyle y=b} ∇ 2 ∇ 2 w = q / D {\displaystyle \nabla ^{2}\nabla ^{2}w=q/D}
라고 가정해 보자.
w ( x , y ) = ∑ m = 1 ∞ Y m ( y ) 죄를 짓다 m π x a . {\displaystyle w(x,y)=\sum _{m=1}^{\nothy_{m}(y)\sin {\frac {m\pi x}{a}\, } For a plate that is simply-supported along x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} w = 0 {\displaystyle w=0} M x x = 0 {\displaystyle M_{xx}=0} ∂ w / ∂ y = 0 {\displaystyle \partial w/\partial y=0} ∂ 2 w / ∂ y 2 = 0 {\displaystyle \partial ^{2}w/\partial y^{2}=0} ∂ 2 w / ∂ x 2 = 0 {\displaystyle \partial ^{2}w/\partial x^{2}=0}
Moments along edges Consider the case of pure moment loading. In that case q = 0 {\displaystyle q=0} w ( x , y ) {\displaystyle w(x,y)} ∇ 2 ∇ 2 w = 0 {\displaystyle \nabla ^{2}\nabla ^{2}w=0}
∂ 4 w ∂ x 4 + 2 ∂ 4 w ∂ x 2 ∂ y 2 + ∂ 4 w ∂ y 4 = 0 . {\displaystyle {\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}=0\,.} Plugging the expression for w ( x , y ) {\displaystyle w(x,y)}
∑ m = 1 ∞ [ ( m π a ) 4 Y m sin m π x a − 2 ( m π a ) 2 d 2 Y m d y 2 sin m π x a + d 4 Y m d y 4 sin m π x a ] = 0 {\displaystyle \sum _{m=1}^{\infty }\left[\left({\frac {m\pi }{a}}\right)^{4}Y_{m}\sin {\frac {m\pi x}{a}}-2\left({\frac {m\pi }{a}}\right)^{2}{\cfrac {d^{2}Y_{m}}{dy^{2}}}\sin {\frac {m\pi x}{a}}+{\frac {d^{4}Y_{m}}{dy^{4}}}\sin {\frac {m\pi x}{a}}\right]=0} or
d 4 Y m d y 4 − 2 m 2 π 2 a 2 d 2 Y m d y 2 + m 4 π 4 a 4 Y m = 0 . {\displaystyle {\frac {d^{4}Y_{m}}{dy^{4}}}-2{\frac {m^{2}\pi ^{2}}{a^{2}}}{\cfrac {d^{2}Y_{m}}{dy^{2}}}+{\frac {m^{4}\pi ^{4}}{a^{4}}}Y_{m}=0\,.} This is an ordinary differential equation which has the general solution
Y m = A m cosh m π y a + B m m π y a cosh m π y a + C m sinh m π y a + D m m π y a sinh m π y a {\displaystyle Y_{m}=A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}+C_{m}\sinh {\frac {m\pi y}{a}}+D_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}} where A m , B m , C m , D m {\displaystyle A_{m},B_{m},C_{m},D_{m}}
w ( x , y ) = ∑ m = 1 ∞ [ ( A m + B m m π y a ) cosh m π y a + ( C m + D m m π y a ) sinh m π y a ] sin m π x a . {\displaystyle w(x,y)=\sum _{m=1}^{\infty }\left[\left(A_{m}+B_{m}{\frac {m\pi y}{a}}\right)\cosh {\frac {m\pi y}{a}}+\left(C_{m}+D_{m}{\frac {m\pi y}{a}}\right)\sinh {\frac {m\pi y}{a}}\right]\sin {\frac {m\pi x}{a}}\,.} Let us choose the coordinate system such that the boundaries of the plate are at x = 0 {\displaystyle x=0} x = a {\displaystyle x=a} y = ± b / 2 {\displaystyle y=\pm b/2} y = 0 {\displaystyle y=0} y = b {\displaystyle y=b} y = ± b / 2 {\displaystyle y=\pm b/2}
w = 0 , − D ∂ 2 w ∂ y 2 y = b / 2 = f 1 ( x ) , − D ∂ 2 w ∂ y 2 y = − b / 2 = f 2 ( x ) {\displaystyle w=0\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr }_{y=b/2}=f_{1}(x)\,,-D{\frac {\partial ^{2}w}{\partial y^{2}}}{\Bigr }_{y=-b/2}=f_{2}(x)} where f 1 ( x ) , f 2 ( x ) {\displaystyle f_{1}(x),f_{2}(x)} symmetrical case where
M y y y = − b / 2 = M y y y = b / 2 {\displaystyle M_{yy}{\Bigr }_{y=-b/2}=M_{yy}{\Bigr }_{y=b/2}} and
f 1 ( x ) = f 2 ( x ) = ∑ m = 1 ∞ E m sin m π x a {\displaystyle f_{1}(x)=f_{2}(x)=\sum _{m=1}^{\infty }E_{m}\sin {\frac {m\pi x}{a}}} we have
w ( x , y ) = a 2 2 π 2 D ∑ m = 1 ∞ E m m 2 cosh α m sin m π x a ( α m tanh α m cosh m π y a − m π y a sinh m π y a ) {\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\cosh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\tanh \alpha _{m}\cosh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}\right)} where
α m = m π b 2 a . {\displaystyle \alpha _{m}={\frac {m\pi b}{2a}}\,.} Similarly, for the antisymmetrical case where
M y y y = − b / 2 = − M y y y = b / 2 {\displaystyle M_{yy}{\Bigr }_{y=-b/2}=-M_{yy}{\Bigr }_{y=b/2}} we have
w ( x , y ) = a 2 2 π 2 D ∑ m = 1 ∞ E m m 2 sinh α m sin m π x a ( α m coth α m sinh m π y a − m π y a cosh m π y a ) . {\displaystyle w(x,y)={\frac {a^{2}}{2\pi ^{2}D}}\sum _{m=1}^{\infty }{\frac {E_{m}}{m^{2}\sinh \alpha _{m}}}\,\sin {\frac {m\pi x}{a}}\,\left(\alpha _{m}\coth \alpha _{m}\sinh {\frac {m\pi y}{a}}-{\frac {m\pi y}{a}}\cosh {\frac {m\pi y}{a}}\right)\,.} We can superpose the symmetric and antisymmetric solutions to get more general solutions.
Simply-supported plate with uniformly-distributed load For a uniformly-distributed load, we have
q ( x , y ) = q 0 {\displaystyle q(x,y)=q_{0}} The deflection of a simply-supported plate with centre ( a 2 , 0 ) {\displaystyle \left({\frac {a}{2}},0\right)}
w ( x , y ) = q 0 a 4 D ∑ m = 1 , 3 , 5 , . . . ∞ ( A m cosh m π y a + B m m π y a sinh m π y a + G m ) sin m π x a where A m = − 2 ( α m tanh α m + 2 ) π 5 m 5 cosh α m B m = 2 π 5 m 5 cosh α m G m = 4 π 5 m 5 and α m = m π b 2 a {\displaystyle {\begin{aligned}&w(x,y)={\frac {q_{0}a^{4}}{D}}\sum _{m=1,3,5,...}^{\infty }\left(A_{m}\cosh {\frac {m\pi y}{a}}+B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}+G_{m}\right)\sin {\frac {m\pi x}{a}}\\\\&{\begin{aligned}{\text{where}}\quad &A_{m}=-{\frac {2\left(\alpha _{m}\tanh \alpha _{m}+2\right)}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&B_{m}={\frac {2}{\pi ^{5}m^{5}\cosh \alpha _{m}}}\\&G_{m}={\frac {4}{\pi ^{5}m^{5}}}\\\\{\text{and}}\quad &\alpha _{m}={\frac {m\pi b}{2a}}\end{aligned}}\end{aligned}}} The bending moments per unit length in the plate are given by
M x = − q 0 π 2 a 2 ∑ m = 1 , 3 , 5 , . . . ∞ m 2 ( ( ( ν − 1 ) A m + 2 ν B m ) cosh m π y a + ( ν − 1 ) B m m π y a sinh m π y a − G m ) sin m π x a {\displaystyle M_{x}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(\nu -1\right)A_{m}+2\nu B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(\nu -1\right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-G_{m}\right)\sin {\frac {m\pi x}{a}}} M y = − q 0 π 2 a 2 ∑ m = 1 , 3 , 5 , . . . ∞ m 2 ( ( ( 1 − ν ) A m + 2 B m ) cosh m π y a + ( 1 − ν ) B m m π y a sinh m π y a − ν G m ) sin m π x a {\displaystyle M_{y}=-q_{0}\pi ^{2}a^{2}\sum _{m=1,3,5,...}^{\infty }m^{2}\left(\left(\left(1-\nu \right)A_{m}+2B_{m}\right)\cosh {\frac {m\pi y}{a}}+\left(1-\nu \right)B_{m}{\frac {m\pi y}{a}}\sinh {\frac {m\pi y}{a}}-\nu G_{m}\right)\sin {\frac {m\pi x}{a}}} Uniform and symmetric moment load For the special case where the loading is symmetric and the moment is uniform, we have at y = ± b / 2 {\displaystyle y=\pm b/2}
M y y = f 1 ( x ) = 4 M 0 π ∑ m = 1 ∞ 1 2 m − 1 sin ( 2 m − 1 ) π x a . {\displaystyle M_{yy}=f_{1}(x)={\frac {4M_{0}}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{2m-1}}\,\sin {\frac {(2m-1)\pi x}{a}}\,.} Displacement (
w {\displaystyle w} )
Bending stress (
σ y y {\displaystyle \sigma _{yy}} )
Transverse shear stress (
σ y z {\displaystyle \sigma _{yz}} )
Displacement and stresses for a rectangular plate under uniform bending moment along the edges
y = − b / 2 {\displaystyle y=-b/2} and
y = b / 2 {\displaystyle y=b/2} . The bending stress
σ y y {\displaystyle \sigma _{yy}} is along the bottom surface of the plate. The transverse shear stress
σ y z {\displaystyle \sigma _{yz}} is along the mid-surface of the plate.
The resulting displacement is
w ( x , y ) = 2 M 0 a 2 π 3 D ∑ m = 1 ∞ 1 ( 2 m − 1 ) 3 cosh α m sin ( 2 m − 1 ) π x a × [ α m tanh α m cosh ( 2 m − 1 ) π y a − ( 2 m − 1 ) π y a sinh ( 2 m − 1 ) π y a ] {\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}} where
α m = π ( 2 m − 1 ) b 2 a . {\displaystyle \alpha _{m}={\frac {\pi (2m-1)b}{2a}}\,.} The bending moments and shear forces corresponding to the displacement w {\displaystyle w}
M x x = − D ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) = 2 M 0 ( 1 − ν ) π ∑ m = 1 ∞ 1 ( 2 m − 1 ) cosh α m × sin ( 2 m − 1 ) π x a × [ − ( 2 m − 1 ) π y a sinh ( 2 m − 1 ) π y a + { 2 ν 1 − ν + α m tanh α m } cosh ( 2 m − 1 ) π y a ] M x y = ( 1 − ν ) D ∂ 2 w ∂ x ∂ y = − 2 M 0 ( 1 − ν ) π ∑ m = 1 ∞ 1 ( 2 m − 1 ) cosh α m × cos ( 2 m − 1 ) π x a × [ ( 2 m − 1 ) π y a cosh ( 2 m − 1 ) π y a + ( 1 − α m tanh α m ) sinh ( 2 m − 1 ) π y a ] Q z x = ∂ M x x ∂ x − ∂ M x y ∂ y = 4 M 0 a ∑ m = 1 ∞ 1 cosh α m × cos ( 2 m − 1 ) π x a cosh ( 2 m − 1 ) π y a . {\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}} The stresses are
σ x x = 12 z h 3 M x x and σ z x = 1 κ h Q z x ( 1 − 4 z 2 h 2 ) . {\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.} Cylindrical plate bending Cylindrical bending occurs when a rectangular plate that has dimensions a × b × h {\displaystyle a\times b\times h} a ≪ b {\displaystyle a\ll b} h {\displaystyle h}
Simply supported plate with axially fixed ends For a simply supported plate under cylindrical bending with edges that are free to rotate but have a fixed x 1 {\displaystyle x_{1}}
Bending of thick Mindlin plates For thick plates, we have to consider the effect of through-the-thickness shears on the orientation of the normal to the mid-surface after deformation. Raymond D. Mindlin's theory provides one approach for find the deformation and stresses in such plates. Solutions to Mindlin's theory can be derived from the equivalent Kirchhoff-Love solutions using canonical relations.[5]
Governing equations The canonical governing equation for isotropic thick plates can be expressed as[5]
∇ 2 ( M − B 1 + ν q ) = − q κ G h ( ∇ 2 w + M D ) = − ( 1 − B c 2 1 + ν ) q ∇ 2 ( ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 ) = c 2 ( ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 ) {\displaystyle {\begin{aligned}&\nabla ^{2}\left({\mathcal {M}}-{\frac {\mathcal {B}}{1+\nu }}\,q\right)=-q\\&\kappa Gh\left(\nabla ^{2}w+{\frac {\mathcal {M}}{D}}\right)=-\left(1-{\cfrac {{\mathcal {B}}c^{2}}{1+\nu }}\right)q\\&\nabla ^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)=c^{2}\left({\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}\right)\end{aligned}}} where q {\displaystyle q} G {\displaystyle G} D = E h 3 / [ 12 ( 1 − ν 2 ) ] {\displaystyle D=Eh^{3}/[12(1-\nu ^{2})]} h {\displaystyle h} c 2 = 2 κ G h / [ D ( 1 − ν ) ] {\displaystyle c^{2}=2\kappa Gh/[D(1-\nu )]} κ {\displaystyle \kappa } E {\displaystyle E} ν {\displaystyle \nu }
M = D [ A ( ∂ φ 1 ∂ x 1 + ∂ φ 2 ∂ x 2 ) − ( 1 − A ) ∇ 2 w ] + 2 q 1 − ν 2 B . {\displaystyle {\mathcal {M}}=D\left[{\mathcal {A}}\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)-(1-{\mathcal {A}})\nabla ^{2}w\right]+{\frac {2q}{1-\nu ^{2}}}{\mathcal {B}}\,.} In Mindlin's theory, w {\displaystyle w} φ 1 {\displaystyle \varphi _{1}} φ 2 {\displaystyle \varphi _{2}} x 2 {\displaystyle x_{2}} x 1 {\displaystyle x_{1}} A = 1 {\displaystyle {\mathcal {A}}=1} B = 0 {\displaystyle {\mathcal {B}}=0} κ {\displaystyle \kappa } 5 / 6 {\displaystyle 5/6}
The solutions to the governing equations can be found if one knows the corresponding Kirchhoff-Love solutions by using the relations
w = w K + M K κ G h ( 1 − B c 2 2 ) − Φ + Ψ φ 1 = − ∂ w K ∂ x 1 − 1 κ G h ( 1 − 1 A − B c 2 2 ) Q 1 K + ∂ ∂ x 1 ( D κ G h A ∇ 2 Φ + Φ − Ψ ) + 1 c 2 ∂ Ω ∂ x 2 φ 2 = − ∂ w K ∂ x 2 − 1 κ G h ( 1 − 1 A − B c 2 2 ) Q 2 K + ∂ ∂ x 2 ( D κ G h A ∇ 2 Φ + Φ − Ψ ) + 1 c 2 ∂ Ω ∂ x 1 {\displaystyle {\begin{aligned}w&=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\left(1-{\frac {{\mathcal {B}}c^{2}}{2}}\right)-\Phi +\Psi \\\varphi _{1}&=-{\frac {\partial w^{K}}{\partial x_{1}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{1}^{K}+{\frac {\partial }{\partial x_{1}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{2}}}\\\varphi _{2}&=-{\frac {\partial w^{K}}{\partial x_{2}}}-{\frac {1}{\kappa Gh}}\left(1-{\frac {1}{\mathcal {A}}}-{\frac {{\mathcal {B}}c^{2}}{2}}\right)Q_{2}^{K}+{\frac {\partial }{\partial x_{2}}}\left({\frac {D}{\kappa Gh{\mathcal {A}}}}\nabla ^{2}\Phi +\Phi -\Psi \right)+{\frac {1}{c^{2}}}{\frac {\partial \Omega }{\partial x_{1}}}\end{aligned}}} where w K {\displaystyle w^{K}} Φ {\displaystyle \Phi } ∇ 2 ∇ 2 Φ = 0 {\displaystyle \nabla ^{2}\nabla ^{2}\Phi =0} Ψ {\displaystyle \Psi } ∇ 2 Ψ = 0 {\displaystyle \nabla ^{2}\Psi =0}
M = M K + B 1 + ν q + D ∇ 2 Φ ; M K := − D ∇ 2 w K Q 1 K = − D ∂ ∂ x 1 ( ∇ 2 w K ) , Q 2 K = − D ∂ ∂ x 2 ( ∇ 2 w K ) Ω = ∂ φ 1 ∂ x 2 − ∂ φ 2 ∂ x 1 , ∇ 2 Ω = c 2 Ω . {\displaystyle {\begin{aligned}{\mathcal {M}}&={\mathcal {M}}^{K}+{\frac {\mathcal {B}}{1+\nu }}\,q+D\nabla ^{2}\Phi ~;~~{\mathcal {M}}^{K}:=-D\nabla ^{2}w^{K}\\Q_{1}^{K}&=-D{\frac {\partial }{\partial x_{1}}}\left(\nabla ^{2}w^{K}\right)~,~~Q_{2}^{K}=-D{\frac {\partial }{\partial x_{2}}}\left(\nabla ^{2}w^{K}\right)\\\Omega &={\frac {\partial \varphi _{1}}{\partial x_{2}}}-{\frac {\partial \varphi _{2}}{\partial x_{1}}}~,~~\nabla ^{2}\Omega =c^{2}\Omega \,.\end{aligned}}} Simply supported rectangular plates For simply supported plates, the Marcus moment sum vanishes, i.e.,
M = 1 1 + ν ( M 11 + M 22 ) = D ( ∂ φ 1 ∂ x 1 + ∂ φ 2 ∂ x 2 ) = 0 . {\displaystyle {\mathcal {M}}={\frac {1}{1+\nu }}(M_{11}+M_{22})=D\left({\frac {\partial \varphi _{1}}{\partial x_{1}}}+{\frac {\partial \varphi _{2}}{\partial x_{2}}}\right)=0\,.} In that case the functions Φ {\displaystyle \Phi } Ψ {\displaystyle \Psi } Ω {\displaystyle \Omega }
w = w K + M K κ G h . {\displaystyle w=w^{K}+{\frac {{\mathcal {M}}^{K}}{\kappa Gh}}\,.} Bending of Reissner-Stein cantilever plates Reissner-Stein theory for cantilever plates[6] q x ( y ) {\displaystyle q_{x}(y)} x = a {\displaystyle x=a}
b D d 4 w x d x 4 = 0 b 3 D 12 d 4 θ x d x 4 − 2 b D ( 1 − ν ) d 2 θ x d x 2 = 0 {\displaystyle {\begin{aligned}&bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=0\\&{\frac {b^{3}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\end{aligned}}} and the boundary conditions at x = a {\displaystyle x=a}
b D d 3 w x d x 3 + q x 1 = 0 , b 3 D 12 d 3 θ x d x 3 − 2 b D ( 1 − ν ) d θ x d x + q x 2 = 0 b D d 2 w x d x 2 = 0 , b 3 D 12 d 2 θ x d x 2 = 0 . {\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+q_{x1}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}-2bD(1-\nu ){\cfrac {d\theta _{x}}{dx}}+q_{x2}=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}=0\quad ,\quad {\frac {b^{3}D}{12}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}=0\,.\end{aligned}}} Solution of this system of two ODEs gives
w x ( x ) = q x 1 6 b D ( 3 a x 2 − x 3 ) θ x ( x ) = q x 2 2 b D ( 1 − ν ) [ x − 1 ν b ( sinh ( ν b a ) cosh [ ν b ( x − a ) ] + tanh [ ν b ( x − a ) ] ) ] {\displaystyle {\begin{aligned}w_{x}(x)&={\frac {q_{x1}}{6bD}}\,(3ax^{2}-x^{3})\\\theta _{x}(x)&={\frac {q_{x2}}{2bD(1-\nu )}}\left[x-{\frac {1}{\nu _{b}}}\,\left({\frac {\sinh(\nu _{b}a)}{\cosh[\nu _{b}(x-a)]}}+\tanh[\nu _{b}(x-a)]\right)\right]\end{aligned}}} where ν b = 24 ( 1 − ν ) / b {\displaystyle \nu _{b}={\sqrt {24(1-\nu )}}/b} w = w x + y θ x {\displaystyle w=w_{x}+y\theta _{x}}
M x x = − D ( ∂ 2 w ∂ x 2 + ν ∂ 2 w ∂ y 2 ) = q x 1 ( x − a b ) − [ 3 y q x 2 b 3 ν b cosh 3 [ ν b ( x − a ) ] ] × [ 6 sinh ( ν b a ) − sinh [ ν b ( 2 x − a ) ] + sinh [ ν b ( 2 x − 3 a ) ] + 8 sinh [ ν b ( x − a ) ] ] M x y = ( 1 − ν ) D ∂ 2 w ∂ x ∂ y = q x 2 2 b [ 1 − 2 + cosh [ ν b ( x − 2 a ) ] − cosh [ ν b x ] 2 cosh 2 [ ν b ( x − a ) ] ] Q z x = ∂ M x x ∂ x − ∂ M x y ∂ y = q x 1 b − ( 3 y q x 2 2 b 3 cosh 4 [ ν b ( x − a ) ] ) × [ 32 + cosh [ ν b ( 3 x − 2 a ) ] − cosh [ ν b ( 3 x − 4 a ) ] − 16 cosh [ 2 ν b ( x − a ) ] + 23 cosh [ ν b ( x − 2 a ) ] − 23 cosh ( ν b x ) ] . {\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&=q_{x1}\left({\frac {x-a}{b}}\right)-\left[{\frac {3yq_{x2}}{b^{3}\nu _{b}\cosh ^{3}[\nu _{b}(x-a)]}}\right]\times \\&\quad \left[6\sinh(\nu _{b}a)-\sinh[\nu _{b}(2x-a)]+\sinh[\nu _{b}(2x-3a)]+8\sinh[\nu _{b}(x-a)]\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&={\frac {q_{x2}}{2b}}\left[1-{\frac {2+\cosh[\nu _{b}(x-2a)]-\cosh[\nu _{b}x]}{2\cosh ^{2}[\nu _{b}(x-a)]}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {q_{x1}}{b}}-\left({\frac {3yq_{x2}}{2b^{3}\cosh ^{4}[\nu _{b}(x-a)]}}\right)\times \left[32+\cosh[\nu _{b}(3x-2a)]-\cosh[\nu _{b}(3x-4a)]\right.\\&\qquad \left.-16\cosh[2\nu _{b}(x-a)]+23\cosh[\nu _{b}(x-2a)]-23\cosh(\nu _{b}x)\right]\,.\end{aligned}}} The stresses are
σ x x = 12 z h 3 M x x and σ z x = 1 κ h Q z x ( 1 − 4 z 2 h 2 ) . {\displaystyle \sigma _{xx}={\frac {12z}{h^{3}}}\,M_{xx}\quad {\text{and}}\quad \sigma _{zx}={\frac {1}{\kappa h}}\,Q_{zx}\left(1-{\frac {4z^{2}}{h^{2}}}\right)\,.} If the applied load at the edge is constant, we recover the solutions for a beam under a concentrated end load. If the applied load is a linear function of y {\displaystyle y}
q x 1 = ∫ − b / 2 b / 2 q 0 ( 1 2 − y b ) d y = b q 0 2 ; q x 2 = ∫ − b / 2 b / 2 y q 0 ( 1 2 − y b ) d y = − b 2 q 0 12 . {\displaystyle q_{x1}=\int _{-b/2}^{b/2}q_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y={\frac {bq_{0}}{2}}~;~~q_{x2}=\int _{-b/2}^{b/2}yq_{0}\left({\frac {1}{2}}-{\frac {y}{b}}\right)\,{\text{d}}y=-{\frac {b^{2}q_{0}}{12}}\,.} See also References ^ Reddy, J. N., 2007, Theory and analysis of elastic plates and shells , CRC Press, Taylor and Francis. ^ Timoshenko, S. and Woinowsky-Krieger, S., (1959), Theory of plates and shells , McGraw-Hill New York. ^ Cook, R. D. et al., 2002, Concepts and applications of finite element analysis , John Wiley & Sons ^ Lévy, M., 1899, Comptes rendues , vol. 129, pp. 535-539 ^ a b Lim, G. T. and Reddy, J. N., 2003, On canonical bending relationships for plates, International Journal of Solids and Structures, vol. 40, pp. 3039-3067. ^ E. Reissner and M. Stein. Torsion and transverse bending of cantilever plates. Technical Note 2369, National Advisory Committee for Aeronautics,Washington, 1951. 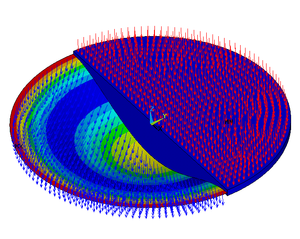

































 플레이트의 중간 부분의 편향이다.
플레이트의 중간 부분의 편향이다. 
![{\displaystyle {\cfrac {\partial ^{4}F}{\partial x^{4}}}+2{\cfrac {\partial ^{4}F}{\partial x^{2}\partial y^{2}}}+{\cfrac {\partial ^{4}F}{\partial y^{4}}}=E\left[\left({\cfrac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\cfrac {\partial ^{2}w}{\partial x^{2}}}{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a797f21006ff4d841374f445a8e54ab2b7fb279)

 스트레스 기능이다.
스트레스 기능이다.  플레이트의 중간 평면으로부터 점의 거리다.
플레이트의 중간 평면으로부터 점의 거리다. 




![\frac{1}{r}\cfrac{d }{d r}\left[r \cfrac{d }{d r}\left\{\frac{1}{r}\cfrac{d }{d r}\left(r \cfrac{d w}{d r}\right)\right\}\right] = -\frac{q}{D}\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)














![\sigma_{rr} = \frac{E}{1-\nu^2}\left[\varepsilon_{rr} + \nu\varepsilon_{\theta\theta}\right] ~;~~
\sigma_{\theta\theta} = \frac{E}{1-\nu^2}\left[\varepsilon_{\theta\theta} + \nu\varepsilon_{rr}\right] ~;~~
\sigma_{r\theta} = 0 \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113afbe187db314e19db5772f1fb7ec65d5f2bf)

![D = 2Eh^3/[3(1-\nu^2)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a71aa263a9aeffc5de8a3eeb37a569a193d2443) , 다음이 있다.
, 다음이 있다. ![\begin{align}
\sigma_{rr} &= -\frac{3qz}{32h^3}\left[(1+\nu)a^2-(3+\nu)r^2\right] \\
\sigma_{\theta\theta} &= -\frac{3qz}{32h^3}\left[(1+\nu)a^2-(1+3\nu)r^2\right]\\
\sigma_{r\theta} &= 0 \,.
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e9eae0c15eb3c3606cfcbfadf7e523df1069eae)
![M_{rr} = -\frac{q}{16}\left[(1+\nu)a^2-(3+\nu)r^2\right] ~;~~
M_{\theta\theta} = -\frac{q}{16}\left[(1+\nu)a^2-(1+3\nu)r^2\right] ~;~~
M_{r\theta} = 0 \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa27857c8e8ae81af9dc56fa29a74b33bc3dad8)






 진폭이고,
진폭이고, 
 (는)
(는) 















 (는) 다음에 의해 주어진 푸리에 계수다.
(는) 다음에 의해 주어진 푸리에 계수다. 







































![\sum_{m=1}^\infty \left[\left(\frac{m\pi}{a}\right)^4 Y_m \sin\frac{m\pi x}{a}
- 2\left(\frac{m\pi}{a}\right)^2 \cfrac{d^2 Y_m}{d y^2} \sin\frac{m\pi x}{a}
+ \frac{d^4Y_m}{dy^4} \sin\frac{m\pi x}{a}\right] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4b7bc6c19d495de8e6086dc8866cf7571b323f9)



![w(x,y) = \sum_{m=1}^\infty \left[
\left(A_m + B_m\frac{m\pi y}{a}\right) \cosh\frac{m\pi y}{a} +
\left(C_m + D_m\frac{m\pi y}{a}\right) \sinh\frac{m\pi y}{a}
\right] \sin \frac{m\pi x}{a} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f35b38c6ddc1b29b74377203666d669c5791b2cc)




















![{\displaystyle {\begin{aligned}&w(x,y)={\frac {2M_{0}a^{2}}{\pi ^{3}D}}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)^{3}\cosh \alpha _{m}}}\sin {\frac {(2m-1)\pi x}{a}}\times \\&~~\left[\alpha _{m}\,\tanh \alpha _{m}\cosh {\frac {(2m-1)\pi y}{a}}-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bb4b518f750d8e1aafd47fb079065c5c4a5786)

![{\displaystyle {\begin{aligned}M_{xx}&=-D\left({\frac {\partial ^{2}w}{\partial x^{2}}}+\nu \,{\frac {\partial ^{2}w}{\partial y^{2}}}\right)\\&={\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\sin {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[-{\frac {(2m-1)\pi y}{a}}\sinh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.\left\{{\frac {2\nu }{1-\nu }}+\alpha _{m}\tanh \alpha _{m}\right\}\cosh {\frac {(2m-1)\pi y}{a}}\right]\\M_{xy}&=(1-\nu )D{\frac {\partial ^{2}w}{\partial x\partial y}}\\&=-{\frac {2M_{0}(1-\nu )}{\pi }}\sum _{m=1}^{\infty }{\frac {1}{(2m-1)\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\,\times \\&~\left[{\frac {(2m-1)\pi y}{a}}\cosh {\frac {(2m-1)\pi y}{a}}+\right.\\&\qquad \qquad \qquad \qquad \left.(1-\alpha _{m}\tanh \alpha _{m})\sinh {\frac {(2m-1)\pi y}{a}}\right]\\Q_{zx}&={\frac {\partial M_{xx}}{\partial x}}-{\frac {\partial M_{xy}}{\partial y}}\\&={\frac {4M_{0}}{a}}\sum _{m=1}^{\infty }{\frac {1}{\cosh \alpha _{m}}}\,\times \\&~\cos {\frac {(2m-1)\pi x}{a}}\cosh {\frac {(2m-1)\pi y}{a}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b46371a14545a06c6bb677179132a02137a8fbb4)







![D = Eh^3/[12(1-\nu^2)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f3bf995e9bb0214179b93d14f38e7e01cf3a671)
![c^2 = 2\kappa G h/[D(1-\nu)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bc4c3ed836ac15ba7c94c0e0fc3cd9fb1d8825a)

![\mathcal{M} = D\left[\mathcal{A}\left(\frac{\partial \varphi_1}{\partial x_1} + \frac{\partial \varphi_2}{\partial x_2}\right)
- (1-\mathcal{A})\nabla^2 w\right] + \frac{2q}{1-\nu^2}\mathcal{B} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/c93657927f897412a7df1207325d3a731bfa9fed)



















![\begin{align}
w_x(x) & = \frac{q_{x1}}{6bD}\,(3ax^2 -x^3) \\
\theta_x(x) & = \frac{q_{x2}}{2bD(1-\nu)}\left[x - \frac{1}{\nu_b}\,
\left(\frac{\sinh(\nu_b a)}{\cosh[\nu_b (x-a)]} + \tanh[\nu_b(x-a)]\right)\right]
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a9eebb0810de812da44e1e62453b7af0aa8dddf)


![\begin{align}
M_{xx} & = -D\left(\frac{\partial^2 w}{\partial x^2}+\nu\,\frac{\partial^2 w}{\partial y^2}\right) \\
& = q_{x1}\left(\frac{x-a}{b}\right) - \left[\frac{3yq_{x2}}{b^3\nu_b\cosh^3[\nu_b(x-a)]}\right]
\times \\
& \quad \left[6\sinh(\nu_b a) - \sinh[\nu_b(2x-a)] +
\sinh[\nu_b(2x-3a)] + 8\sinh[\nu_b(x-a)]\right] \\
M_{xy} & = (1-\nu)D\frac{\partial^2 w}{\partial x \partial y} \\
& = \frac{q_{x2}}{2b}\left[1 -
\frac{2+\cosh[\nu_b(x-2a)] - \cosh[\nu_b x]}{2\cosh^2[\nu_b(x-a)]}\right] \\
Q_{zx} & = \frac{\partial M_{xx}}{\partial x}-\frac{\partial M_{xy}}{\partial y} \\
& = \frac{q_{x1}}{b} - \left(\frac{3yq_{x2}}{2b^3\cosh^4[\nu_b(x-a)]}\right)\times
\left[32 + \cosh[\nu_b(3x-2a)] - \cosh[\nu_b(3x-4a)]\right. \\
& \qquad \left. - 16\cosh[2\nu_b(x-a)] +
23\cosh[\nu_b(x-2a)] - 23\cosh(\nu_b x)\right]\,.
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23db4b670f6da6f2f18a0e2419ca828fbc73d657)



