사냥 진동

철도 차륜에서의 사냥 진동

사냥 진동이란 평형에 대한 자기 스케일링으로, 대개 원치 않는 것이다.^[1] 이 표현은 19세기에 사용되었고 평형을 위한 시스템이 어떻게 "사냥"되는지 묘사하고 있다.^[1] 이 표현은 전자, 항공, 생물학, 철도 공학 등 다양한 분야의 현상을 묘사하기 위해 사용된다.^[1]

철도 바퀴 세트

고전적인 사냥 진동(classic hunting or gogie hunting)은 부착 철도의 방향 안정성이 좌우되는 사기 작용에 의해 야기되는 철도 차량(흔히 트럭 사냥 또는 보기 사냥이라고 불림)의 흔들림 운동이다. 접착력과 관성력의 상호작용에서 발생한다. 저속에서는 유착이 지배하지만 속도가 증가함에 따라 유착력과 관성력은 규모 면에서 비교할 수 있게 되고 임계 속도에서 진동이 시작된다. 이 속도 이상에서는 움직임이 폭력적일 수 있으며 트랙과 바퀴를 손상시키고 탈선을 일으킬 수 있다. 차이는 드물지만 동일한 각도로 회전하는 휠셋의 양쪽 휠에 따라 동작이 달라지기 때문에 디퍼렌셜이 있는 시스템에서는 문제가 발생하지 않는다. 탈고 350호와 같은 일부 열차는 차이가 없지만 대부분의 바퀴가 서로 독립적으로 회전하기 때문에 대부분 사냥용 진동에는 영향을 받지 않는다. 그러나 동력차의 바퀴는 기존 보그처럼 2인 1조로 차축에 고정되기 때문에 사냥 진동으로 인해 영향을 받을 수 있다. 서로 독립적으로 회전하고 쌍으로 차축에 고정되지 않는 독립형 바퀴가 장착된 덜 원뿔형 바퀴와 보그가 열차의 보그에 적합한 차동보다 저렴하다.^[2]

이 문제는 19세기 말에 처음으로 주목되었는데, 그 때 열차 속도가 그것을 접할 수 있을 만큼 빨라졌다. 1930년대에 이에 대응하기 위한 진지한 노력이 진행되어, 길어진 트럭과 측면 드램핑 스윙 행거 트럭이 생겨났다. 일본 신칸센의 개발에서는, 트럭 설계 속도를 225 km/h (140 mph) 이상으로 연장하기 위해 덜 원뿔적인 바퀴와 다른 설계 변경을 이용했다. 유럽과 일본의 연구 개발 노력에 기초한 휠 및 트럭 설계의 발전은 강철 휠 시스템의 속도를 신칸센의 원래 신칸센보다 훨씬 더 크게 확장시켰으며, 반면 역호환성의 이점은 호버트레인이나 마글레브 시스템과 같은 대안보다 그러한 기술이 우세하게 유지되고 있다. 강철 바퀴 열차의 속도 기록은 프랑스 TGV가 574.9km/h(357mph)로 보유하고 있다.

키네마틱 분석

Diagram, from the front, of a laterally displaced wheelset on rails (modelled as circles). Labels: on a line of circumference of the wheel, "Position of point of contact for straight running"; on the radius of that circumference, "Nominal radius"; on the distance between that circumference and the top of the rail, "Lateral displacement"; overall: "Centre of curvature is the intersection of the line of contact and the wheelset centreline".

철도 바퀴 연결 작용의 운동학

정성적 설명은 현상에 대한 이해를 제공하지만, 더 깊은 이해는 필연적으로 차량 역학의 수학적 분석을 필요로 한다. 해도 결과는 근사치일 뿐이다.

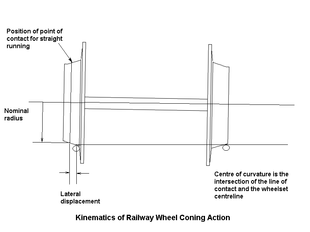
운동학적 설명은 운동 기하를 유발하는 힘을 참조하지 않고 운동 기하를 다루기 때문에 직선 트랙에서 주행하는 휠 세트의 기하학적 설명으로 분석이 시작된다. 뉴턴의 두 번째 법칙은 신체의 가속과 힘을 연관시키기 때문에 작용하는 힘은 그 성분의 가속도를 계산하여 운동학에서 도출될 수 있다. 그러나 이러한 힘이 (이 경우에서와 같이) 운동학적 설명을 변경하면 결과는 근사적으로만 정확할 수 있다.

가정 및 비물질적 설명

이 동역학적 설명은 힘을 무시하기 때문에 여러 가지 간단한 가정을 만든다. 첫째로, 롤링 저항은 0이라고 가정한다. (열차나 트럭에 부착되지 않은) 휠셋은 직선적이고 평평한 트랙에서 앞으로 밀린다. 바퀴가 흔들리기 시작하고, 힘이 없기 때문에 결코 속도가 느려지지 않는다. 트랙을 고수하고 미끄러지지 않도록 바퀴가 아래로 내려가는 힘 제외). 처음에 바퀴셋이 철로 중심에 있다면 각 바퀴의 유효 지름은 같으며 바퀴셋은 완전히 직선으로 영원히 선로를 따라 굴러 내려간다. 그러나 휠셋이 약간 중심을 벗어나 유효 직경(또는 반지름)이 다르면 휠셋이 반지름의 곡선으로 이동하기 시작한다. R (이 휠셋 반지름 등에 표시되며, 나중에 파생될 것). 문제는 운동학적 추론을 이용해 바퀴의 궤적을 찾거나, 더 정확히 말하면 바퀴의 중심 궤적을 트랙의 중앙 노반에 수직으로 투사하는 것이다. 이것은 평평한 지구 표면의 평면에 그려진 궤적이다. x-y 그래픽 플롯 위치 x 철도를 따라가는 거리, 그리고 y 선로 중앙을 따라 흐르는 철도의 직선(두 레일 사이의 간격)에서 휠셋 중심 편차인 "차단 오차"이다.

바퀴자국 궤적이 곡선을 따라가는 것을 설명하기 위해 평평한 테이블 상판에 못이나 나사를 놓고 밀면 된다. 손톱이나 나사가 지름이 극도로 다른 바퀴를 가진 바퀴와 같기 때문에 원형 곡선으로 굴러갈 것이다. 머리는 큰 직경의 바퀴와 유사하고 뾰족한 끝은 작은 직경의 바퀴와 같다. 못이나 나사가 전체 원을 그리며 회전하는 동안(그리고 그 이상) 철도 바퀴 세트는 서로 다르게 동작한다. 왜냐하면 그것이 커브에서 회전하기 시작하자마자, 효과적인 직경은 경로의 곡률을 감소시키는 방식으로 변화하기 때문이다. "반경"과 "곡선"은 바퀴의 궤적의 곡률을 의미하며, 철도의 곡률은 완벽히 직선이기 때문에 철도의 곡률을 의미하지 않는다. 바퀴셋이 굴러감에 따라 바퀴가 유효 직경이 동일하고 경로는 더 이상 굴곡되지 않는 지점에 도달할 때까지 곡률은 감소한다. 그러나 궤적은 이 지점에서 경사(트랙의 중심선 위로 대각선으로 교차하는 직선)를 가지고 있어 트랙의 중심선과 유효 직경 역방향(이전의 더 작은 직경의 바퀴가 더 큰 직경이 되고 반대로)을 오버슈팅한다. 이로 인해 휠셋이 반대 방향으로 곡선을 그리며 이동하게 된다. 다시 그것은 중심선을 오버슈팅하고 이 현상은 바퀴셋이 좌우로 진동하면서 무한정 계속된다. 휠 플랜지는 절대로 레일에 접촉하지 않는다는 점에 유의하십시오. 이 모델에서 레일은 항상 레일 헤드의 동일한 선을 따라 휠 트레드와 접촉하는 것으로 가정되며, 레일은 레일이 칼날 가장자리라고 가정하고 선(영폭)을 따라 휠 트레드와만 접촉한다.

수학적 분석

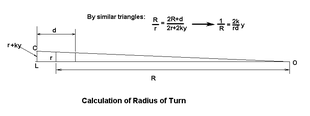
그 기차는 원뿔형 바퀴 자국으로 선로에 머무른다. 휠셋이 양만큼 한쪽으로 이동된 경우 y (추적 오류), 한쪽의 레일에 접촉하는 트레드의 반경은 감소되는 반면 다른 한쪽의 트레드는 증가된다. 각 속도는 양쪽 휠에 대해 동일하므로(이 휠은 리지드 액슬을 통해 결합됨), 직경이 큰 트레드는 속도를 높이는 반면 작은 휠은 속도를 늦춘다. 바퀴 세트는 원뿔의 발생기가 레일 위의 바퀴와 접촉하는 지점을 통과하고 바퀴 세트의 축을 통과하여 정의된 곡률 중심 주위를 조향한다. 비슷한 삼각형을 적용하면 턴 반경에 대해 알 수 있다.

턴 반지름 계산

{\frac {1}{R}={\frac {2ky}{rd}}}

, where d 트랙 게이지, r 직진 시 휠 반지름 k 트레드 테이퍼(트랙에 수직인 수평 방향 트레드 경사)

직선 트랙에 상대적인 휠 세트의 경로는 함수에 의해 정의된다. y(x)) 어디에 x 트랙을 따라 나아가는 것이다. 이것을 추적 오류라고도 한다.^[3] 움직임 방향이 레일과 어느 정도 평행하게 유지된다면, 경로의 곡률은 다음 두 번째 파생 모델과 관련이 있을 수 있다. y 대략^[4] 트랙을 따라가는 거리에 관해서.

\왼쪽 {\frac {\operatorname {d}{2}y}{\operatorname {d}x^{2}}}\오른쪽 \protected {\frac {1}{R}}}}}}

트랙을 따라가는 궤적은 다음과 같은 방정식에 의해 관리된다.^[5]

{\frac {\d}^{2}y}{\d}x^{2}}=-\좌측값\frac {2k}{rd}\오른쪽)y

이것은 파장을 갖는 단순한 조화 운동이다.

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

=

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

{\

클링겔 공식으로 알려진

\lambda =2\pi {\sqrt {\frac {rd}{2k}}}

(1883년 파생)^[6]

이 운동학적 분석은 기차가 항상 좌우로 흔들린다는 것을 암시한다. 사실, 이 진동은 임계 속도 이하로 감쇠되고 그에 상응하여 승차감이 더 편안하다. 운동학적 결과는 운동을 일으키는 힘을 무시한다. 이것들은 크리프(비선형) 개념을 사용하여 분석할 수 있지만 접촉 지역의 휠과 레일의 탄성 왜곡에서 발생하기 때문에 단순하게 정량화하기는 다소 어렵다. 이것들은 마찰 접촉 역학의 주제다; 이러한 효과를 사냥 움직임 분석에서 포함하는 초기 발표는 카터에 의해 발표되었다.^[7] 역사적 개요는 노데를^[8] 참조하십시오.

움직임이 레일(Rail)과 실질적으로 평행인 경우, 휠 세트 $\left(\theta \right)$ ) ${\$ 의 각도 변위는 다음과 같이 주어진다 $\left(\theta \right)$ .

\theta ={\frac {\frac 이름 {d} y}{\propername {d}x}

따라서 다음과 같다.

{\displaystyle{\begin{정렬}{\frac{\operatorname{d}\theta}{\operatorname{d}x}}&={\frac{\operatorname{d}^{2}y}{\operatorname{d}x^{2}}}=-\left({\frac{2k}{rd}}\right)y\\{\frac{\operatorname{d}^{2}\theta}{\operatorname{d}x^{2}}}&=-\left({\frac{2k}{rd}}\right){\frac{\operatorname{d}는 y}{\operatorname{d}x}}=-\left({\frac. {2k}{rd}}}\오른쪽)\theta \end{aigned}}

각도 편향은 또한 단순한 조화 운동을 따르는데, 이것은 좌우 운동보다 1/4 사이클 정도 뒤처진다. 서로 다른 두 상태(이 경우 차축 요 편향과 측면 변위)를 포함하는 조화 동작으로 특징지어지는 많은 시스템에서, 두 동작 사이의 1/4 사이클 지연은 시스템이 전방 동작에서 에너지를 추출할 수 있는 능력을 갖도록 한다. 이러한 효과는 철도 차량 사냥뿐만 아니라 항공기 날개의 "날개"와 도로 차량의 "흔들림"에서 관찰된다. 위에서 도출한 키네마틱 솔루션은 임계 속도에서의 움직임을 설명한다.

실제로 임계 속도 이하에서는 두 동작 사이의 지연이 1/4 사이클 미만이므로 모션이 감쇠되지만 임계 속도 이상에서는 1/4 사이클 이상이면 모션이 증폭되게 된다.

관성력을 추정하기 위해서는 거리파생상품을 시간파생상품으로 표현할 필요가 있다. 이 작업은 차량 속도를 사용하여 수행된다. U, 상수라고 가정하는 경우:

{\frac {\frac 이름 {d}{\d} t}=U{\frac {\operatorname {d}{\operatorname {d} x}}

요(Yaw)에서 차축의 각도 가속도는 다음과 같다.

{\frac {\d}^{2}\theta }{d}{d} t^{2}}=-U^{2}\왼쪽({\frac {2k}{rd}\오른쪽)\tta

관성 모멘트(자이로스코프 효과 무시)는 다음과 같다.

{\displaystyle Fd=C{\frac {\operatorname {d} ^{2}\theta }{\operatorname {d} t^{2}}:

, where F 레일을 따라 작용하는 힘이 C 휠 세트의 관성 모멘트가 된다.

F=-CU^{2}\왼쪽({\frac {2k}{rd^{2}}\오른쪽)\theta

바퀴와 레일 사이의 최대 마찰력은 다음과 같다.

F=\mu {\frac {W}{2}}:

, where W 축하중이며 $[\displaystyle \mu }$ 은 $\mu$ (는) 마찰계수다. 총 미끄러짐은 다음과 같이 속도 및 차축 편향의 조합에서 발생한다.

\theta U^{2}=\mu W{\frac {rd^{2}}{4Ck}}

이 표현은 임계 속도를 상당히 과대평가하지만, 사냥이 일어나는 물리적 이유, 즉 관성력이 특정 속도 이상의 부착력과 비교 가능하게 되는 것을 보여준다. 마찰 제한은 이 경우 접착력을 잘 나타내지 못한다.

실제 접착력은 접촉 부위의 트레드 및 레일의 변형에서 발생한다. 총 미끄러짐은 없으며, 탄성 왜곡과 국부적 미끄러짐(크립 미끄러짐)이 있을 뿐이다. 정상운전중 이 힘은 제한 마찰제한치 이내에 있다. 완전한 분석은 롤링 접촉 역학 이론을 사용하여 이러한 힘을 고려한다.

그러나 동역학적 분석은 차륜-레일 접촉에서 미끄러짐이 전혀 없다고 가정했다. 이제 휠셋(클링겔 공식에 따른)의 계산된 사인곡선 궤적을 정확하게 맞추지 못하는 약간의 크리프 미끄러짐이 있다는 것이 명백해졌다.

에너지 균형

임계 속도의 추정치를 얻기 위해서는 이 키네마틱 솔루션이 유효한 조건이 주위와의 순에너지 교환이 없는 경우에 해당하므로 시스템의 운동 에너지와 잠재적 에너지를 고려함으로써 임계 속도를 도출할 수 있어야 한다는 사실을 이용한다.

허용:

\omega ={\frac {\buffername {d} \teta }{\buffername {d} t}

연산자 사용:

\omega{\frac {\d}{\dname {d} \d} \theta }={\frac 이름 {d}{\fracname {d} t}}

각도 가속 방정식은 각도 속도의 관점에서 요, $\omega$ , ${\displaystyle \omega$

\omega{\frac {\d} \omega }{}{\operatorname {d} \theta }}=-U^{2}\왼쪽({\frac {2k}{rd}\right)\ta

통합:

{\frac {1}{1}:{2}}:\omega^{2}=-{\frac {1}{2}}:U^{2}\왼쪽({\frac {2k}{rd}\오른쪽)\theta ^{2}

따라서 회전으로 인한 운동 에너지는 다음과 같다.

{\frac {1}{2}}C\omega^{2}=-{\frac {1}{2}}CU^{2}\왼쪽({\frac {2k}{rd}}\오른쪽)\theta ^{2}

Diagram, from above, of an angled wheelset withrespect to the rails. The angle of the wheel set with respect to the rails is labelled theta; the rail gauge is labelled d; the spacing of the points of contact is labelled d over cos theta.

액슬 요와 접촉점의 외부 이동

액슬이 흔들리면 접촉 지점이 윤간거리에서 바깥쪽으로 이동하여 액슬 높이가 낮아진다. 지지점 사이의 거리는 다음과 같이 증가한다.

{\frac {d}{cos(\theta )}=d\left(1+{\frac {1}{1}:{1}}\the ^{2}\오른쪽)

(소량 2차로). 디딤판 중심에서 지적되는 지지점의 변위는 다음과 같다.

{\frac {1}{1}{2}}\왼쪽(d+{\frac {1}{1}{2}}d\theta ^{2}-d\오른쪽)

축하중이 감소하다.

h={\frac {1}{4}kd\theta ^{2}

따라서 액슬 하중을 낮춰 수행하는 작업은 다음과 같다.

E={\frac {1}{4}Wkd\theta ^{2}

이것은 시스템에서 손실된 에너지이므로 움직임이 계속되기 위해서는 휠셋의 전방 운동에서 동일한 양의 에너지를 추출해야 한다.

외부 휠 속도는 다음과 같이 지정된다.

V={\frac {U}{r}}\왼쪽(r+ky\오른쪽)

운동 에너지는 다음과 같다.

{\frac {1}{4}m\왼쪽(U^{2}+2)U^{2}{\frac {ky}{r}}}+U^{2}{\frac {k^{2}y^{2}}:{r^{2}}:}\오른쪽)}

내륜을 위하여

{\frac {1}{4}m\좌측(U^{2}-2U^{2}{2}{\frac {ky}{r}}}}+)U^{2}{\frac {k^{2}y^{2}}:{r^{2}}:}\오른쪽)}

, where m 양쪽 바퀴의 질량이다.

운동 에너지의 증가는 다음과 같다.

\delta E={\frac {1}{1}{2}}m\왼쪽({\frac {Uky}{r}\오른쪽)^{2}

이 운동은 전방 운동에서 추출한 에너지가 0요에서 설정된 휠의 운동 에너지 증가가 최대 요에서 차축 하중에 의해 손실되는 잠재적 에너지와 동일한 한 일정한 진폭으로 계속된다.

이제 운동학자들로부터:

{\reasoned}2U{\frac {ky}{{rd}}&=\omega \\delta E&={\frac {1}{8}md^{2}\omega ^{2}\ended}}}}}}

그렇지만

\omega^{2}=-U^{2}\왼쪽({\frac {2k}{rd}\오른쪽)\the ^{2}

변환 운동 에너지는

\delta E=-{\frac {1}{8}U^{2}md^{2}\왼쪽({\frac {2k}{rd}\오른쪽)\the ^{2}

총 운동 에너지는 다음과 같다.

T={\frac {1}{2}}U^{2}\왼쪽(C+{\frac {md^{2}}:{4}\오른쪽)\왼쪽({\frac {2k}{rd}\오른쪽)\theta ^{2}

임계 속도는 에너지 균형에서 확인할 수 있다.

{\frac {Wkd}{2}}=U^{2}{\frac {2k}{rd}}}\왼쪽(C+{\frac {md^{2}}:{4}\오른쪽)

따라서 임계 속도는 다음과 같다.

U^{2}={\frac {Wrd^{2}}{4C+md^{2}}}}

이는 휠 테이퍼와 무관하지만 액슬 하중 대 휠 설정 질량의 비율에 따라 달라진다. 트레드가 정말로 원뿔형이라면 임계 속도는 테이퍼와 무관할 것이다. 실제로 바퀴의 마모는 접지면 폭에 따라 테이퍼가 달라지게 하므로 잠재적 에너지를 결정하는 데 사용되는 테이퍼 값이 운동에너지를 계산하는 데 사용되는 값과 다르다. 전자를 로 칭함 a, 임계 속도는 다음과 같다.

U^{2}={\frac {Ward^{2}}{k(4C+md^{2})}

, where a 이제 휠 마모에 의해 결정되는 형상 요인이 된다. 이 결과는 Wickens(1965)에서 표준 제어 엔지니어링 방법을 사용한 시스템 동적 분석에서 도출되었다.^[9]

단순 분석의 한계

바퀴 세트의 움직임은 이 분석이 나타내는 것보다 훨씬 더 복잡하다. 차량 서스펜션에^[10] 의해 가해지는 추가적인 구속력이 있으며, 고속에서는 휠 세트가 추가적인 자이로스코프 토크를 생성하여 임계 속도의 추정치를 수정한다. 일반적으로 철도 차량은 고속 주행 시 안정성이 불안정한 형태로 변화할 때 저속 주행 시 안정성이 유지된다. 철도 차량 시스템 역학의 비선형 분석의 주요 목적은 접선 선로에서 철도 차량의 분기, 비선형 횡방향 안정성 및 수렵 거동에 대한 해석 조사의 관점을 보여주는 것이다. 이 연구는 분석을 위한 보골류보프 방법을 설명한다.^[11]

두 가지 중요한 문제, 즉 몸을 고정된 지지체로 가정하고 사냥속도를 계산하는 비선형 요소의 영향력은 대부분 연구에 집중되어 있다.^[12] 실제 철도 차량은 자유도가 훨씬 더 높으며, 결과적으로 둘 이상의 임계 속도를 가질 수 있다; 가장 낮은 차량이 바퀴셋 운동에 의해 지시된다는 것은 결코 확실하지 않다. 그러나 이 분석은 사냥이 왜 일어나는지를 보여 주기 때문에 유익하다. 속도가 증가함에 따라 관성력은 접착력과 견줄 수 있게 된다. 그렇기 때문에 임계 속도는 바퀴 세트 질량(관성력을 결정하는)에 대한 차축 하중(접착력)의 비율에 따라 달라진다.

또는 특정 속도 이하에서는 전진 운동에서 추출한 에너지가 차축을 낮춰 손실된 에너지를 대체하기에 불충분하며, 이 속도 이상에서는 추출된 에너지가 잠재적 에너지 손실보다 크고 진폭이 축적된다.

최대 차축 요에서의 잠재적 에너지는 차축의 요 모션에 탄성 구속조건을 포함시킴으로써 증가될 수 있으며, 따라서 스프링 장력에 의한 기여가 있다. 바퀴의 요운동에 대한 구속조건을 높이기 위해 바퀴를 보그로 배열하고, 보지에 탄성 구속조건을 적용하는 것도 임계 속도를 높인다. 이 방정식에 탄성력을 도입하면 고전적인 사냥보다는 총 미끄러짐의 시작에 의해서만 제한되는 현수 설계가 허용된다. 사냥의 가상적 제거에 대해 지불해야 할 벌금은 직선적인 것으로, 수반되는 선로설비 문제와 레거시 인프라와의 양립불가능성이 있다.

사냥은 적어도 원칙적으로는 트랙의 질에 적응할 수 있는 적극적인 피드백 조절에 의해 해결될 수 있는 역동적인 문제다. 그러나 능동 제어의 도입은 신뢰성과 안전성 문제를 제기한다.

사냥이 시작된 직후 총 미끄러짐이 발생하고 바퀴가 레일 위에 부딪혀 양쪽에 손상을 줄 가능성이 있다.

도로-철도

독립형 레일 휠 차축은 도로-철도 차량에 공통임

많은 도로-철도 차량은 각 레일 휠에 독립적인 차축과 서스펜션 시스템을 갖추고 있다. 이를 레일에 로드 휠이 있는 것과 결합하면 위의 공식을 사용하는 것이 어려워진다. 역사적으로, 도로-철도 차량에는 앞바퀴가 약간 토인(to-in)으로 설정되어 있으며, 이는 차량을 레일에서 주행하는 동안 사냥을 최소화하는 것으로 밝혀졌다.

참고 항목

이 종류의 문제를 다루는 일반적인 방법은 다음을 참조하십시오.

제어공학

참조

^ ^a ^b ^c Oxford English Dictionary (2nd ed.). Oxford University Press. 1989. f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state.
^ https://www.talgo.com/en/rolling-stock/very-high-speed/350/
^ 바퀴의 경로가 트랙을 따라 절대적으로 똑바로 달리고 바퀴 쌍이 트랙을 중심으로 움직이면 추적 오차는 0이 된다.
^ 수학적 자세한 내용은 함수의 곡면성#그래프를 참조하십시오. 대략적인 평등은 추적 오류가 있을 때만 평등하게 된다. y에 대해 기울기가 0인 경우 x. 추적 오류는 사인파로 밝혀지기 때문에 0 기울기의 지점은 최대 추적 오류 지점에 있다. y. 그러나 평등이 거의 정확하다. 단, 평등의 경사가 다음과 같다면. y 낮음.
^ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\$ 2} $y}{\operatorname {d}$ x $^{2}}:$ 음수임 ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ y 긍정적이고 반대다. 에 대한 다른 방정식 R, ${\frac {1}{R}}={\frac {2ky}{rd}}$ R ${\frac {1}{R}}={\frac {2ky}{rd}}$ = ${\frac {1}{R}}={\frac {2ky}{rd}}$ ${\frac {1}{R}}={\frac {2ky}{rd}}$ ${\frac {1}{R}}={\frac {2ky}{rd}}$ d ${\$ 은(는) 다음 시간 동안 유지되지 않음 ${\frac {1}{R}}={\frac {2ky}{rd}}$ y 반경이니까 음성이야 R (수학적 정의에 따라) 음수가 될 수 없다. 하지만 반경이 지나면 R 두 방정식을 조합하여 제거하면 다음과 같은 두 가지 경우를 확인함으로써 결과 방정식이 정확해진다. y 부정적이고 y 양성의
^ 이우니키, p.7 공식 2.1
^ Carter, F. W. (July 25, 1928). "On the Stability of Running of Locomotives". Proceedings of the Royal Society. A. 121 (788): 585–610. Bibcode:1928RSPSA.121..585C. doi:10.1098/rspa.1928.0220.
^ Knothe, K. (2008). "History of wheel/rail contact mechanics: from Redtenbacher to Kalker". Vehicle System Dynamics. 46 (1–2): 9–26. doi:10.1080/00423110701586469. S2CID 109580328.
^ Wickens, A. H. (1965–66). "The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability". Proceedings of the Institution of Mechanical Engineers: 29–.
^ Wickens, A. H.; Gilchrist, A. O.; Hobbs, A. E. W. (1969–70). "Suspension Design for High-Performance Two-Axle Freight Vehicles". Proceedings of the Institution of Mechanical Engineers: 22–.
^ Serajian, Reza (2013). "Parameters' changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie". Journal of Measurements in Engineering: 195–206.
^ Serajian, Reza (2011). "Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory". Int J Auto Engng: 186–196.

Iwnicki, Simon (2006). Handbook of railway vehicle dynamics. CRC Press.
Shabana, Ahmed A.; et al. (2008). Railroad vehicle dynamics : a computational approach. CRC Press.
Wickens, A H (Jan 1, 2003). Fundamentals of rail vehicle dynamics : guidance and lateral stability. Swets & Zeitlinger.
Serajian, Reza (2013). Parameters' changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie. CRC Press.
Serajian, Reza (2011). Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory. CRC Press.

[OED-1] Oxford English Dictionary (2nd ed.). Oxford University Press. 1989. f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state.

[2] ttps://www.talgo.com/en/rolling-stock/very-high-speed/350/

[3] 바퀴의 경로가 트랙을 따라 절대적으로 똑바로 달리고 바퀴 쌍이 트랙을 중심으로 움직이면 추적 오차는 0이 된다.

[4] 수학적 자세한 내용은 함수의 곡면성#그래프를 참조하십시오. 대략적인 평등은 추적 오류가 있을 때만 평등하게 된다. y에 대해 기울기가 0인 경우 x. 추적 오류는 사인파로 밝혀지기 때문에 0 기울기의 지점은 최대 추적 오류 지점에 있다. y. 그러나 평등이 거의 정확하다. 단, 평등의 경사가 다음과 같다면. y 낮음.

[5] ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ ${\$ 2} $y}{\operatorname {d}$ x $^{2}}:$ 음수임 ${\frac {\operatorname {d} ^{2}y}{\operatorname {d} x^{2}}}$ y 긍정적이고 반대다. 에 대한 다른 방정식 R, ${\frac {1}{R}}={\frac {2ky}{rd}}$ R ${\frac {1}{R}}={\frac {2ky}{rd}}$ = ${\frac {1}{R}}={\frac {2ky}{rd}}$ ${\frac {1}{R}}={\frac {2ky}{rd}}$ ${\frac {1}{R}}={\frac {2ky}{rd}}$ d ${\$ 은(는) 다음 시간 동안 유지되지 않음 ${\frac {1}{R}}={\frac {2ky}{rd}}$ y 반경이니까 음성이야 R (수학적 정의에 따라) 음수가 될 수 없다. 하지만 반경이 지나면 R 두 방정식을 조합하여 제거하면 다음과 같은 두 가지 경우를 확인함으로써 결과 방정식이 정확해진다. y 부정적이고 y 양성의

[6] 이우니키, p.7 공식 2.1

[Carter1928-7] Carter, F. W. (July 25, 1928). "On the Stability of Running of Locomotives". Proceedings of the Royal Society. A. 121 (788): 585–610. Bibcode:1928RSPSA.121..585C. doi:10.1098/rspa.1928.0220.

[Knothe2008-8] Knothe, K. (2008). "History of wheel/rail contact mechanics: from Redtenbacher to Kalker". Vehicle System Dynamics. 46 (1–2): 9–26. doi:10.1080/00423110701586469. S2CID 109580328.

[Wickens1965-9] Wickens, A. H. (1965–66). "The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability". Proceedings of the Institution of Mechanical Engineers: 29–.

[10] Wickens, A. H.; Gilchrist, A. O.; Hobbs, A. E. W. (1969–70). "Suspension Design for High-Performance Two-Axle Freight Vehicles". Proceedings of the Institution of Mechanical Engineers: 22–.

[11] Serajian, Reza (2013). "Parameters' changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie". Journal of Measurements in Engineering: 195–206.

[12] Serajian, Reza (2011). "Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory". Int J Auto Engng: 186–196.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Search