피트니스 풍경

Fitness landscape
다음에 대한 시리즈 일부
진화생물학
Darwin's finches by Gould.jpg
존 굴드(John Gould)에 의한 다윈의 지느러미
프로세스 및 결과
박물학
진화론의 역사
필드 및 응용 프로그램
사회적 의미

진화생물학에서는 건강경관이나 적응경관(진화경관의 유형)을 사용하여 유전자형과 생식성공 사이의 관계를 시각화한다. 모든 유전자형은 잘 정의된 복제율(흔히 피트니스라고 한다)을 가지고 있다고 가정한다. 이 피트니스는 경치의 "높이"이다. 비슷한 유전형은 서로 '가까운' 반면, 매우 다른 유전형은 '멀다'고 한다. 가능한 모든 유전자형, 그 유사성 정도, 그리고 그것과 관련된 피트니스 가치의 집합을 피트니스 풍경이라고 부른다. 피트니스 풍경에 대한 생각은 동물들의 초정상적인 자극에 대한 반응과 같은 공훈과 결함을 포함하여 자연 선택에 의해 진화의 결함 있는 형태를 설명하는 것을 돕는 은유다.

피트니스 가치의 분포를 일종의 풍경으로 시각화하여 진화를 연구하자는 발상은 1932년 세월 라이트에 의해 처음 소개되었다.[1]

진화적 최적화 문제에서 피트니스 환경은 모든 후보 솔루션에 대한 피트니스 기능의 평가(아래 참조)이다.

생물학에서

피트니스 풍경 스케치. 화살표는 지형에 있는 모집단의 선호 흐름을 나타내며, 지점 A와 C는 국부적 최적점이다. 붉은 공은 매우 낮은 피트니스 가치에서 피크 상단으로 이동한 인구를 나타낸다.

모든 피트니스 풍경에서 키는 피트니스에 대한 시각적 은유와 상징이다. 비록 각각의 경우 거리가 서로 다른 정도를 나타내고 비유하지만, 다른 차원을 특징짓는 세 가지 뚜렷한 방법이 있다.[2]

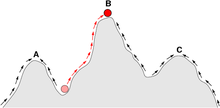
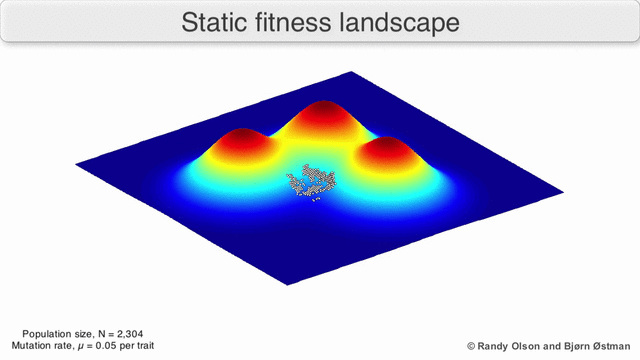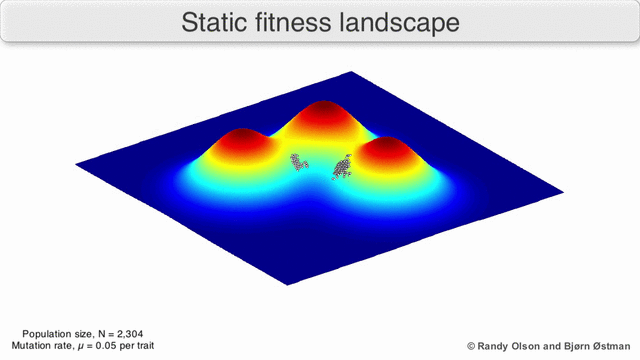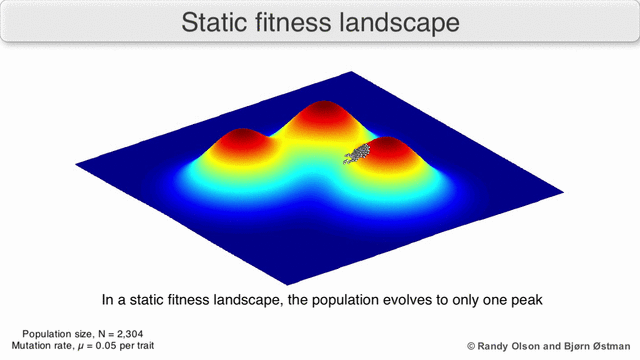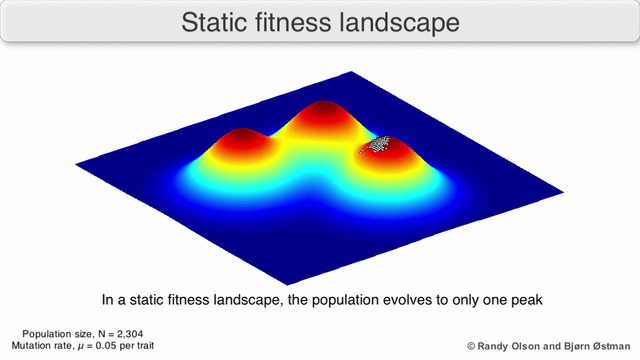
피트니스 풍경은 종종 산맥으로 여겨진다. 지역 봉우리(모든 길이 내리막인 지점, 즉 체력 저하를 위한 지점)와 계곡(많은 길이 오르막으로 이어지는 지역)이 존재한다. 깊은 계곡으로 둘러싸인 많은 지역 봉우리들이 있는 피트니스 경관을 험준하다고 한다. 만약 모든 유전자형이 동일한 복제율을 가지고 있다면, 반면에, 피트니스 풍경은 평평하다고 한다. 진화하는 인구는 일반적으로 피트니스 환경에서 일련의 작은 유전적 변화에 의해 무한한 시간 제한에서 지역 최적치에 도달할 때까지 오르막길을 오른다.

지역 최적화는 진화 시간에도 항상 발견될 수 없다는 점에 유의하십시오. 지역 최적화가 합리적인 시간 내에 발견될 수 있다면 피트니스 환경을 "쉬운"이라고 하고, 필요한 시간이 기하급수적인 경우 피트니스 환경을 "힘든"[3]이라고 부른다. 경직된 경관은 미로처럼 생긴 성질이 특징인데, 이 성질은 한때 유익했던 대립이 유해해져 진화가 퇴보할 수밖에 없게 된다. 그러나 생물학적으로 영감을 받은 피트니스 풍경에 미로 같은 성질의 존재는 힘든 풍경을 만들기에 충분하지 않을 수 있다.[4]

NK 피트니스 환경의 2차원 시각화. 화살은 피트니스 환경에서 진화하는 동안 인구가 따를 수 있는 다양한 돌연변이 경로를 나타낸다.

피트니스 환경에 대한 유전자형

라이트는 유전자형 공간을 하이퍼큐브처럼 시각화했다.[1] 연속 유전자형 "치수"는 정의되지 않았다. 대신에 유전자형의 네트워크는 돌연변이 경로를 통해 연결된다.

스튜어트 카우프만의 NK 모델은 이러한 피트니스 환경의 범주에 속한다. 선택-가중유도 그래프(SWAG)와 같은 새로운 네트워크 분석 기법도 차원 없는 유전자형 공간을 사용한다.[5]

피트니스 환경에 대한 빈도 감소

라이트의 수학적 연구는 체력을 알레르기의 함수로 묘사했다.[2] 여기서 각 차원은 다른 유전자에서 알레르 주파수를 설명하고 0과 1 사이에 간다.

피트니스 환경에 대한 표현형

세 번째 종류의 피트니스 풍경에서, 각각의 차원은 다른 표현형질을 나타낸다.[2] 정량적 유전학의 가정 하에, 이러한 표현적 치수는 유전자형에 매핑될 수 있다. 피트니스 환경에 대한 표현 유형의 예는 아래 시각화를 참조하십시오.

진화적 최적화에서

진화 생물학 분야와는 별개로 피트니스 풍경의 개념은 유전 알고리즘이나 진화 전략과 같은 진화 최적화 방법에서도 중요성이 높아졌다. 진화적 최적화에서는 생물학적 진화의 역학을 모방하여 실제의 문제(예를 들어 공학적 또는 물류적 문제)를 해결하려고 한다. 예를 들어, 다수의 목적지 주소를 가진 배달 트럭은 다양한 경로를 취할 수 있지만, 아주 극소수만이 운전 시간이 짧을 것이다.

많은 일반적인 형태의 진화적 최적화를 사용하기 위해서는 관심 문제에 대한 가능한 모든 해결책(즉, 배달 트럭의 경우 가능한 모든 경로)이 얼마나 '좋은' 것인지 정의해야 한다. 이것은 스칼라 값 함수 f(scalar 값어치는 f(s)가 0.3과 같은 단순한 숫자인 반면 s는 더 복잡한 물체, 예를 들어 배달 트럭의 경우 목적지 주소 목록)를 도입함으로써 이루어지는데, 이를 피트니스 기능이라고 한다.

높은 f는 s가 좋은 해결책임을 암시한다. 배달 트럭의 경우, f는 경로 s의 시간당 배달 횟수가 될 수 있다. 가장 좋은, 또는 적어도 아주 좋은 해결책은 다음과 같은 방법으로 발견된다: 처음에, 무작위 해결책의 집단이 만들어진다. 그런 다음, 만족스러운 해결책이 발견될 때까지, 그 해결책은 변형되고 더 건강한 사람들을 위해 선택된다.

진화적 최적화 기법은 특히 단일 솔루션의 품질을 판단하기는 쉽지만 가능한 모든 솔루션을 하나하나 거치기 어려운 상황에서 유용하다(배달 트럭의 특정 경로의 주행 시간을 결정하는 것은 쉽지만, 일단 1회 1회 1회 1회 1회 1회 2회 1회 1회 1회 1회 2회 1회 1회 1회 1회 1회 1회 1회 1회 1회 1회 1회 1회 모든 가능한 경로를 확인하는 것은 거의 불가능하다.목적지의 수가 한둘이상으로 증가하다.

피트니스 기능을 정의하기 어려운 경우에도 피트니스 환경의 개념은 유용할 수 있다. 예를 들어, 체력 평가가 확률적 표본 추출에 의한 것이라면, 표본 추출은 각 지점의 (일반적으로 알려지지 않은) 분포에서 나온 것이다. 그럼에도 불구하고, 각 지점에서 예상되는 적합성에 의해 형성된 경관을 추론하는 데 유용할 수 있다. 피트니스가 시간(동적 최적화)에 따라 또는 환경의 다른 종(공진화)과 함께 변화한다면, 즉각적인 피트니스 환경의 궤도에 대해 추론하는 것이 여전히 유용할 수 있다. 그러나 일부의 경우(예: 선호 기반 대화형 진화 연산) 인간 선호도가 단일 피트니스 과제와 일치한다는 보장이 없기 때문에 관련성이 더 제한적이다.

스칼라 가치의 피트니스 함수의 개념 f(s)는 물리학에서 잠재적 또는 에너지 함수의 개념과도 일치한다. 두 개념은 물리학자들이 전통적으로 잠재적 기능을 최소화하는 관점에서만 생각한다는 점에서 차이가 있을 뿐, 생물학자들은 적합성이 극대화되고 있다는 개념을 선호한다. 따라서 잠재적 함수의 역수를 취하면 피트니스 함수로 변하게 되고, 그 반대로도[citation needed] 변하게 된다.

주의사항 및 제한사항

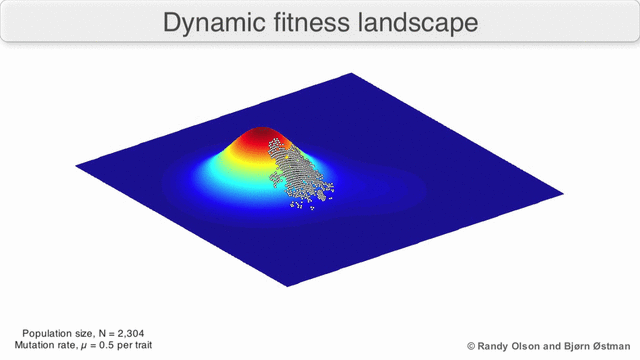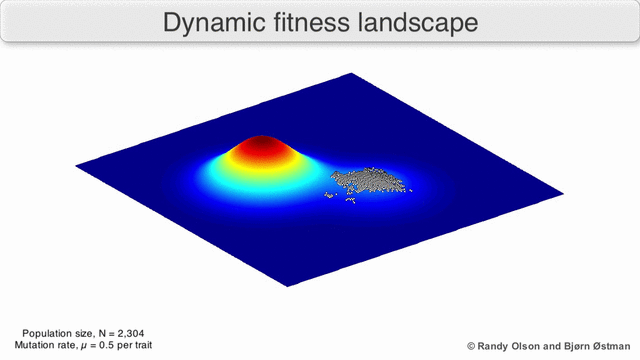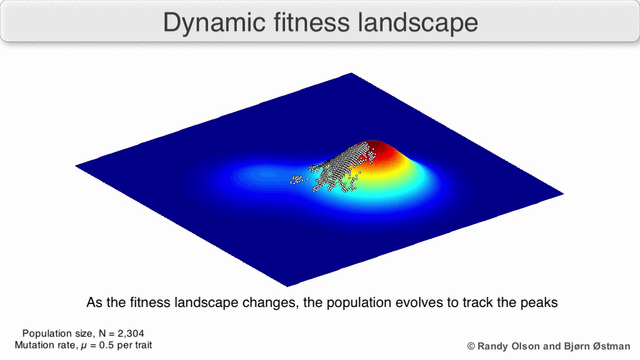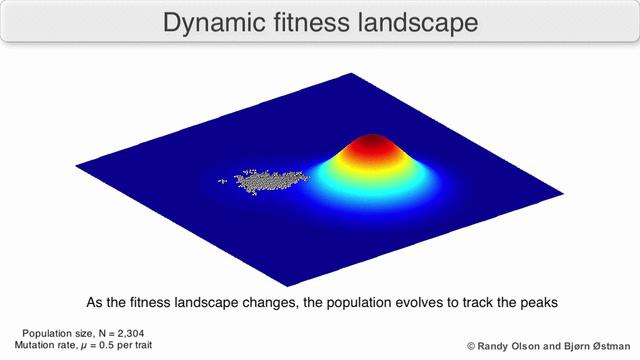
몇 가지 중요한 주의사항이 존재한다. 인간의 정신은 3차원 이상의 관점에서 생각하기 때문에 3D 위상은 고도로 다차원적인 피트니스 환경을 논할 때 잘못 이끌 수 있다.[6][7] 특히 자연적인 생물학적 피트니스 풍경의 최고봉이 그러한 다차원적 풍경의 피트니스 계곡에 의해 진정으로 분리되는 것인지, 아니면 그것들이 엄청나게 긴 중립적 능선에 의해 연결되어 있는 것인지는 명확하지 않다.[8][9] 게다가, 피트니스 풍경은 시간에 따라 정적이 아니라 다른 유전자의 변화하는 환경과 진화에 의존한다.[5] 따라서 그것은 바다 경관에 가까우며,[10] 적응 피크가 실제로 어떻게 분리될 수 있는지에 더 큰 영향을 미친다. 또한, 경관이 일반적으로 절대적인 것이 아니라 상대적인 기능이라는 점을 고려하는 것이 목적적합하다.[11] 마지막으로 효소를 논할 때 건강을 위한 대용물로 기능을 이용하는 것이 일반적이기 때문에, 어떤 난잡한 활동도 유기체의 궁극적인 적합성을 함께 결정하게 되는 겹치는 풍경으로서 존재하며, 공존하는 서로 다른 상대적 풍경 사이의 차이를 암시한다.[12]

이러한 한계를 염두에 두고, 피트니스 환경은 여전히 진화에 대한 교육적인 사고방식이 될 수 있다. 경관 내구성 및 피크 수, 높이, 분리, 클러스터링의 매개변수 중 일부를 (시각화하지 않더라도) 근본적으로 측정할 수 있다. 단순화된 3D 경관을 서로 상대적으로 사용하여 관련 특징을 시각적으로 나타낼 수 있다. 또한, 진화 경로의 작은 하위 집합의 피트니스 환경은 실험적으로 구성되고 시각화되어 피트니스 피크나 계곡과 같은 잠재적으로 드러나는 특징을 나타낼 수 있다.[5] 진화 경로의 피트니스 환경은 일련의 개별 돌연변이들 사이에서 가능한 진화 단계와 종말점을 나타낸다.

Visualization of a population evolving in a static fitness landscape Visualization of a population evolving in a dynamic fitness landscape

참고 항목

참조

  1. ^ Jump up to: a b Wright, Sewall (1932). "The roles of mutation, inbreeding, crossbreeding, and selection in evolution" (PDF). Proceedings of the Sixth International Congress on Genetics. 1 (8): 355–66.
  2. ^ Jump up to: a b c Provine, William B. (1986). Sewall Wright and Evolutionary Biology. University of Chicago Press.[페이지 필요]
  3. ^ Kaznatcheev, Artem (2019). "Computational Complexity as an Ultimate Constraint on Evolution". Genetics. 212 (1): 245–265. doi:10.1534/genetics.119.302000. PMC 6499524. PMID 30833289.
  4. ^ Bertram, Jason; Masel, Joanna (April 2020). "Evolution Rapidly Optimizes Stability and Aggregation in Lattice Proteins Despite Pervasive Landscape Valleys and Mazes". Genetics. 214 (4): 1047–1057. doi:10.1534/genetics.120.302815. PMC 7153934. PMID 32107278.
  5. ^ Jump up to: a b c Steinberg, B; Ostermeier, M (2016). "Environmental changes bridge evolutionary valleys". Science Advances. 2 (1): e1500921. Bibcode:2016SciA....2E0921S. doi:10.1126/sciadv.1500921. PMC 4737206. PMID 26844293.
  6. ^ McCandlish, David M (2011). "Visualizing Fitness Landscapes". Evolution. 65 (6): 1544–58. doi:10.1111/j.1558-5646.2011.01236.x. PMC 3668694. PMID 21644947.
  7. ^ McGhee, George R. (2006). The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces. ISBN 978-1-139-45995-2.[페이지 필요]
  8. ^ Gavrilets, S. (2004). Fitness Landscapes and the Origin of Species. Princeton University Press. ISBN 978-0-691-11983-0.[페이지 필요]
  9. ^ Kaplan, Jonathan (2008). "The end of the adaptive landscape metaphor?". Biology & Philosophy. 23 (5): 625–38. doi:10.1007/s10539-008-9116-z. S2CID 170649453.
  10. ^ Mustonen, Ville; Lässig, Michael (2009). "From fitness landscapes to seascapes: Non-equilibrium dynamics of selection and adaptation". Trends in Genetics. 25 (3): 111–9. doi:10.1016/j.tig.2009.01.002. PMID 19232770.
  11. ^ Woodcock, Glenn; Higgs, Paul G (1996). "Population Evolution on a Multiplicative Single-Peak Fitness Landscape". Journal of Theoretical Biology. 179 (1): 61–73. doi:10.1006/jtbi.1996.0049. PMID 8733432.
  12. ^ Diaz Ochoa, Juan G (2017). "Elastic Multi-scale Mechanisms: Computation and Biological Evolution". Journal of Molecular Evolution. 86 (1): 47–57. Bibcode:2018JMolE..86...47D. doi:10.1007/s00239-017-9823-7. PMID 29248946. S2CID 22624633.

외부 링크

시각화된 피트니스 환경의 예
추가 읽기