조력
Tidal force조력( force力)은 다른 물체와의 중력장의 경사(강도의 차이)로 인해 다른 물체의 질량 중심을 향해 선을 따라 물체가 늘어나는 중력 효과로, 조수, 조석 잠금, 천체 이탈, 고리형성 등 다양한 현상을 일으킨다.로체 한계, 극단적인 경우 물체의 스파게티화.그것은 다른 물체에 의해 한 물체에 가해지는 중력장이 그 부분들에 걸쳐 일정하지 않기 때문에 발생한다: 가장 가까운 쪽이 가장 먼 쪽보다 더 강하게 끌어당긴다.바로 이 차이가 몸을 스트레칭하게 만드는 것이다.따라서, 조력 또한 중력장의 2차 효과뿐만 아니라 미분력으로도 알려져 있다.
천체역학에서, 조력이라는 표현은 물체나 물질(예를 들어, 조력)이 주로 두 번째 물체(예: 지구)의 중력에 의해 영향을 받는 상황을 나타낼 수 있지만, 세 번째 물체(예: 달)의 중력에 의해 교란되기도 한다.이러한 경우에 교란력은 때때로 조력이라고[2] 불립니다: 그것은 세 번째 물체에 의해 두 번째 물체에 의해 가해지는 힘과 세 번째 물체에 의해 첫 번째 [3]물체에 의해 가해지는 힘의 차이입니다.
설명.
본체(본체1)가 다른 본체(본체2)의 중력에 의해 작용하면 본체2의 측과 본체2에서 떨어진 측 사이에서 본체1의 전계가 크게 달라질 수 있다.그림 4는 다른 물체(바디 2)에 의해 가해지는 구형 물체(바디 1)에 대한 중력의 차이를 나타낸다.이러한 소위 조력이라고 불리는 힘은 두 신체에 무리를 주고, 그것들을 왜곡시키거나 심지어 극단적인 경우, 한쪽 또는 다른 한쪽을 [4]갈라놓을 수도 있다.로체 한계란 행성으로부터의 중력의 차이가 물체의 일부를 서로 [5]끌어당기는 힘을 상쇄하기 때문에 조석 효과가 물체를 분해하는 행성으로부터의 거리입니다.만약 중력장이 균일하다면 이러한 변형은 일어나지 않을 것이다. 왜냐하면 균일한 장은 단지 몸 전체가 같은 방향과 같은 속도로 함께 가속하게 하기 때문이다.
크기와 거리
천문체의 크기와 다른 물체와의 거리는 조력의 [6]크기에 큰 영향을 미칩니다.지구와 같은 천체에 작용하는 조력은 그 천체의 지름에 정비례하고 달이나 태양과 같은 중력을 발생시키는 다른 천체로부터의 거리의 세제곱에 반비례합니다.욕조, 수영장, 호수 및 기타 작은 수역에서의 조석 작용은 무시할 [7]수 있다.
그림 3은 거리에 따라 중력이 어떻게 감소하는지 보여주는 그래프입니다.이 그래프에서 인력은 거리의 제곱에 비례하여 감소하지만 값에 대한 기울기는 거리에 비례하여 감소합니다.이것이 바로 어떤 점에서의 경사나 조력이 거리의 세제곱에 반비례하는 이유이다.
조석력은 그래프상의 두 점 사이의 Y의 차이에 해당하며, 한 점은 본체의 가까운 쪽에 있고 다른 점은 먼 쪽에 있습니다.두 점이 더 멀리 떨어져 있거나 그래프에서 더 왼쪽에 있을 때, 즉 유인 물체에 더 가깝다는 것을 의미할 때 조력은 더 커집니다.
예를 들어, 태양이 달보다 지구에 더 큰 중력을 가함에도 불구하고, 달은 지구에 태양보다 더 큰 조력을 발생시킨다. 왜냐하면 기울기가 작기 때문이다.
중력은 근원으로부터의 거리의 제곱에 반비례한다.끌어당기는 인력은 물체의 근원쪽에서 더 강해지고, 근원쪽에서 떨어진 쪽에서는 더 약해집니다.조력은 [7]차이에 비례한다.
태양, 지구, 달
예상대로, 아래 표는 달에서 지구까지의 거리가 지구에서 달까지의 거리와 같다는 것을 보여준다.지구는 달보다 81배 더 크지만 반지름은 대략 4배이다.결과적으로, 같은 거리에서, 달 표면에서의 지구의 조력은 지구 [8]표면에서의 달의 조력보다 약 20배 더 강하다.
| 조력을 일으키는 중력체 | 조력을 받는 물체 | 직경 및 거리 | 조력 | |||
|---|---|---|---|---|---|---|
| 몸 | 질량(m) | 몸 | 반지름(r) | 거리(d) | ||
| 태양. | 1.99×10kg30 | 지구 | 6.37×106 m | 1.50×1011 m | 3.81×10−27 m−2 | 5.05×10−7 mµs−2 |
| 달 | 7.34×1022 kg | 지구 | 6.37×106 m | 3.84×108 m | 2.24×10−19 m−2 | 1.10×10−6 mµs−2 |
| 지구 | 5.97×1024 kg | 달 | 1.74×106 m | 3.84×108 m | 6.12×10−20 m−2 | 2.44×10−5 ms−2 |
| m은 질량, r은 반지름, d는 거리, 2r은 지름 | ||||||
영향들
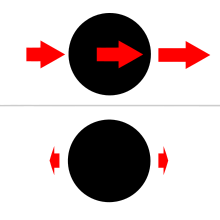
탄성구가 극히 작은 경우, 조력의 효과는 체적의 변화 없이 체형을 변형시키는 것이다.구체는 두 개의 돌출부가 있는 타원체가 되어 다른 물체를 가리키고 멀어지게 됩니다.더 큰 물체는 타원형으로 뒤틀리고 약간 압축되는데, 이것이 달의 작용으로 지구의 바다에 일어나는 현상이다.지구와 달은 질량의 공통 중심 또는 중력의 중심에서 회전하며, 그들의 중력은 이 운동을 유지하는 데 필요한 구심력을 제공한다.지구의 관찰자에게, 이 중심에서 매우 가까운 곳에 있는 상황은 물체 1이 물체 2인 달의 중력에 의해 작용되는 지구 중 하나입니다.지구의 모든 부분은 달의 중력에 의해 영향을 받으며, 바다에 있는 물이 재분배되어 달 근처와 [11]달에서 멀리 떨어진 면에 부풀어 오른다.
물체가 조력을 받으면서 회전할 때 내부 마찰로 인해 회전 운동 에너지가 점차 열로 소실됩니다.지구와 지구의 달의 경우, 회전 운동 에너지의 손실은 세기당 약 2밀리초의 이득을 가져옵니다.만약 천체가 그것의 1차적인 것에 충분히 가까이 있다면, 이것은 지구의 달의 경우와 같이 궤도 운동에 조석적으로 고정된 회전을 야기할 수 있다.조석열은 목성의 달 이오에 극적인 화산 효과를 일으킨다.조석력에 의한 스트레스는 또한 지구의 [6]달에서 매달 규칙적으로 일어나는 지진의 패턴을 야기한다.
조석력은 해류에 기여하는데, 해류는 극지방으로 열에너지를 전달함으로써 지구의 온도를 낮춘다.조력 변화는 6년에서 10년 [12]간격의 지구 온도 기록의 차가운 기간과 관련이 있으며, 조력 변화의 조화로운 비트 변화는 밀레니엄 기후 변화에 기여할 수 있다고 제안되었다.지금까지 밀레니얼 기후 변화와 강한 연관성은 발견되지 않았다.[13]
조석 효과는 중성자별이나 블랙홀과 같은 질량이 큰 작은 물체 근처에서 특히 두드러지며, 그곳에서 유입되는 물질의 "스파게티화"의 원인이 된다.조석력은 지구 대양의 해양 조류를 생성하는데, 여기서 끌어당기는 물체는 달이고, 더 적은 정도는 태양이다.조력 또한 조력 고정, 조력 가속, 조력 가열의 원인이 된다.조수는 또한 지진성을 유발할 수 있다.
지구 내부에서 전도성 유체를 생성함으로써, 조력 또한 지구의 [14]자기장에 영향을 미친다.
공식화
소정의 (외부적으로 생성된) 중력장에 대해 소정의 점에서의 중력가속도(동일한 장에 의한)로부터 소정의 물체 중심에서의 중력가속도(소정의 외부발생장에 의한)를 벡터 감산함으로써 물체에 대한 조석가속도는 소정의 점에서의 중력가속도에 의한 것이다.이에 대응하여 조력이라는 용어는 조력가속도에 의한 힘을 표현하기 위해 사용된다.이러한 목적을 위해 고려되는 유일한 중력장은 외부 중력장입니다; 물체의 중력장은 관련이 없습니다. (즉, 비교는 주어진 지점과 그 지점에서 불균등하게 작용하는 외부에서 생성된 장이 없는 경우일 수 있습니다.)e 기준 본체의 중심.외부에서 생성된 장은 일반적으로 지구 중심 기준 프레임에서 지구 표면 위 또는 위에 있는 점의 빈번한 예에서 종종 태양이나 달이 교란하는 제3의 물체에 의해 생성된다.)
조석 가속은 회전이나 궤도를 도는 물체를 필요로 하지 않는다. 예를 들어, 물체는 여전히 (변화하는) 조석 가속의 영향을 받으면서도 중력장의 영향을 받아 직선으로 자유 낙하할 수 있다.
뉴턴의 만유인력의 법칙과 운동법칙에 따라 질량구 M의 중심에서 R 거리에 있는 질량체는 F g
a {\
서 r {\은(는) 바디 M에서 바디 M을 가리키는 단위 벡터입니다(여기서 M에서 M까지의 가속은 음수 부호가 있음).
이제 질량 m의 본체 근처에 있는 입자가 경험하는 질량 M의 구에 의한 가속도를 생각해 보자.R을 M의 중심에서 m의 중심까지의 거리로 하여 δr을 질량 m의 중심에서 입자의 (상대적으로 작은) 거리라고 한다.단순화를 위해, 거리는 먼저 질량 M의 구를 향하거나 멀어지는 방향으로만 고려된다.질량 m의 본체가 반지름 θr의 구면일 경우, 고려된 새로운 입자는 질량 M의 구 중심으로부터 거리(R ± θr)의 표면에 위치할 수 있으며, M으로부터의 거리가 R보다 클 경우 θr은 양으로 간주할 수 있다.m의 질량에 따라 입자가 m을 향해 경험할 수 있는 중력 가속도는 제쳐두고, M을 향한 중력에 의한 입자의 가속도는 다음과 같습니다.
분모에서 R항을2 추출하면 다음과 같은 결과가 나옵니다.
Maclaurin 시리즈 /( ± ) {{ 1/ \ x )^{는 1 + 3 2∓ {\ \ 1 \ + ^ { )입니다. \cdots} - 다음 일련의 확장을 제공합니다.
첫 번째 항은 기준 의 중심에 있는 M에 의한 중력 가속도이다 즉, rr이 0인 지점이다.M과 관련하여 m(및 그 표면의 모든 물체)이 자유 낙하 상태이기 때문에 이 용어는 m 표면에서 관측된 입자의 가속도에 영향을 미치지 않는다.원입자에 가해지는 힘을 근입자에 가해지는 힘에서 빼면 이 첫 번째 항은 다른 모든 짝수 항과 마찬가지로 취소됩니다.나머지(잔존) 항은 위에서 언급한 차이를 나타내며 조력(가속) 항이다.R에 비해 θr이 작을 경우 첫 번째 잔차항 이후의 항은 매우 작으며 무시할 수 있으며, m과 M의 중심을 연결하는 축을 따라 θr에 대한 대략적인 a axial{\이 된다.
이와 같이 계산하면 θr이 m과 M의 중심을 연결하는 축을 따른 거리인 경우 {\은 m의 중심(θr은 0)으로 바깥쪽으로 향한다.
또한 벡터 계산을 필요로 하는 물체 m과 물체 M을 연결하는 축에서 떨어진 곳에서 조력 가속도를 계산할 수도 있다.이 축에 수직인 평면에서는 조석가속도가 안쪽으로 향하며(θr이 0인 중앙을 가리키며), 그 크기는 4와 같이 1 2 axial { {\이다.
태양계의 행성 표면에서의 조석 가속은 일반적으로 매우 작다.예를 들어, 달-지구 축을 따라 지구 표면에서의 달 조석 가속도는 약 1.1×10g인−7 반면, 태양-지구 축을 따라 지구 표면에서의 태양 조석 가속도는 약−7 0.52×10g이다. 여기서 g는 지구 표면에서의 중력 가속도이다.따라서 태양에 의한 조력(가속)은 달의 [16]조력(가속)지구 표면에서의 태양 조석 가속은 프린키아의 [17]뉴턴에 의해 처음 주어졌다.
「 」를 참조해 주세요.
레퍼런스
- ^ "Hubble Views a Cosmic Interaction". nasa.gov. NASA. February 11, 2022. Retrieved 2022-07-09.
- ^ I. N. Avsiuk, "소련 천문학 편지", 제3권(1977년), 96-99페이지.
- ^ M. L. Kutner(2003) "천문학의 물리적 관점" 페이지 509를 참조한다.
- ^ R Penrose (1999). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. p. 264. ISBN 978-0-19-286198-6.
tidal force.
- ^ Thérèse Encrenaz; J -P Bibring; M Blanc (2003). The Solar System. Springer. p. 16. ISBN 978-3-540-00241-3.
- ^ a b "The Tidal Force Neil deGrasse Tyson". www.haydenplanetarium.org. Retrieved 2016-10-10.
- ^ a b Sawicki, Mikolaj (1999). "Myths about gravity and tides". The Physics Teacher. 37 (7): 438–441. Bibcode:1999PhTea..37..438S. CiteSeerX 10.1.1.695.8981. doi:10.1119/1.880345. ISSN 0031-921X.
- ^ Schutz, Bernard (2003). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (illustrated ed.). Cambridge University Press. p. 45. ISBN 978-0-521-45506-0. 45페이지 발췌
- ^ "2018 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ R. S. MacKay; J. D. Meiss (1987). Hamiltonian Dynamical Systems: A Reprint Selection. CRC Press. p. 36. ISBN 978-0-85274-205-1.
- ^ Rollin A Harris (1920). The Encyclopedia Americana: A Library of Universal Knowledge. Vol. 26. Encyclopedia Americana Corp. pp. 611–617.
- ^ Keeling, C. D.; Whorf, T. P. (5 August 1997). "Possible forcing of global temperature by the oceanic tides". Proceedings of the National Academy of Sciences. 94 (16): 8321–8328. Bibcode:1997PNAS...94.8321K. doi:10.1073/pnas.94.16.8321. PMC 33744. PMID 11607740.
- ^ Munk, Walter; Dzieciuch, Matthew; Jayne, Steven (February 2002). "Millennial Climate Variability: Is There a Tidal Connection?". Journal of Climate. 15 (4): 370–385. Bibcode:2002JCli...15..370M. doi:10.1175/1520-0442(2002)015<0370:MCVITA>2.0.CO;2.
- ^ "Hungry for Power in Space". New Scientist. 123: 52. 23 September 1989. Retrieved 14 March 2016.
- ^ "Inseparable galactic twins". ESA/Hubble Picture of the Week. Retrieved 12 July 2013.
- ^ The Admiralty (1987). Admiralty manual of navigation. Vol. 1. The Stationery Office. p. 277. ISBN 978-0-11-772880-6., 제11장, 페이지 277
- ^ 뉴튼, 이삭(1729년).자연 철학의 수학적 원리.Vol2. 우편 307. 아이 에스비엔 978-0-11-772880-6. 3Proposition36, Page307뉴턴,로 표시하는에 대해 이익률 0.52에×120010−7 g이 힘이 Sun-Earth 축을 따라 바다를 모으는 것이다"두번만큼 큰"(즉, 2~38604600)을 써 준 힘 곳 90도 태양으로부터"138604600에"(감속의 관점에서)에서 먼 바닷길을 했다. 그 텍스트 안에.
외부 링크
- 케이스 웨스턴 리저브 대학의 J. 크리스토퍼 미호스의 중력 조수
- 오디오: Cain/Gay – Astronomy Cast Tind Force – 2007년 7월
- Gray, Meghan; Merrifield, Michael. "Tidal Forces". Sixty Symbols. Brady Haran for the University of Nottingham.
- Pau Amaro Seoane. "Stellar collisions: Tidal disruption of a star by a massive black hole". Retrieved 2018-12-28.
- 존 A의 미콜라지 사위키의 중력과 조수에 관한 신화.로건 대학과 콜로라도 대학입니다.
- Donald E의 Tidal Oversions.시마네크


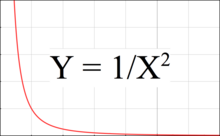









 (는) 바디 M에서 바디
(는) 바디 M에서 바디 

 1
1



 된다.
된다.
 m의 중심(θr은 0)으로 바깥쪽으로 향한다.
m의 중심(θr은 0)으로 바깥쪽으로 향한다.  .
. 



