Korteweg-de Vries 방정식의 비선형적이고 정확한 주기적인 파동해
파나마 해안 과 가까운 얕은 물에서 거의 주기적 으로 부풀어 오르는 미군 폭격기(1933년).뾰족한 볏과 매우 평평한 기압골이 중파도의 특징이다. 유체역학 에서, 중심파(cnoidal wave)는 Korteweg-de Vries 방정식의 비선형적 이고 정확 한 주기적 인 파동해이다.이 해들은 야코비 타원 함수 cn의 관점에서 볼 때, 그래서 이들이 noidal wave라고 불리는 것입니다. 그것들은 수심에 비해 상당히 긴 파장 의 표면 중력파를 묘사 하는 데 사용된다.
코르테베그 와 드 브리에스는 1895년 논문에서 분산형 장파 방정식(현재는 코르테베그-드 브리에스 방정식)을 제안했다.무한 파장의 한계 에서는, 편두파가 단독파 가 된다.
Benjamin-Bona-Mahony 방정식 은 Korteweg-de Vries 방정식에 비해 단파장 거동을 개선했으며, 편파 해법을 사용하는 또 다른 단방향 파동 방정식이다.또한 Korteweg-de Vries 방정식은 단방향 전파 의 경우 Bousinesq 방정식에 대한 근사치이므로 Cnoidal wave는 Bousinesq 방정식에 대한 근사치이다.
중성파 용액은 예를 들어 플라즈마 [1] 이온 음파를 설명 하기 위해 표면 중력파 이외의 다른 응용 분야에서도 나타날 수 있다.
사인파보 다 더 날카로운 볏과 평평 한 기압골이 특징인 노이드파.표시된 경우 타원 모수는 m = 0.9 입니다. 건널목은 거의 치명적인 파도 열차로 구성되어 있습니다 . 사진 은 대서양 프랑스 일드레(레섬 ) 서쪽 지점의 파레스 데 베일린(고래 등대)에서 찍은 사진.배경 코르테베그-데브리, 벤자민-보나-마호니 방정식 Le Méhauté(1976)[2] 밝은 파란색 영역은 편파 이론의 유효성을 나타내고, 공기파 이론 의 경우 밝은 노란색이며, 파선 파란색은 스토크스의 파동 이론에서 요구 되는 순서 사이를 구분합니다. 광회색 음영 기능은 높은 파동(H > hbreaking H)에 대해 5차 스트림 기능 이론을 사용하여 수치 근사치를 통해 범위 확장을 제공합니다. Korteweg – de Vries 방정식(KdV 방정식)은 유체층 표면 중력파의 평균 수심과 비교하여 긴 파장을 갖는 약한 비선형 및 긴 파장의 단방향 전파를 설명하기 위해 사용할 수 있다.KdV 방정식은 주파수 분산 및 진폭 분산 효과를 모두 포함 하는 분산파 방정식입니다. KdV 방정식은 통상적으로 평균 수심h 의 약 5배를 넘는 파장h, 즉 θ > 5시간 , 7h g (\ displaystyle \scriptstyle sqrt {h/g}}) 기간 θ 에 중력가속도 [3] 경우 에 적용할 수 있다. 고전파 근사치 범위 내에서 KdV 방정식의 위치를 예상하기 위해 다음과 같은 방법으로 자신을 구별한다.
Korteweg – de Vries 방정식 - δ > 7h 의 긴 파장에 대해 약한 비선형 및 분산파의 전진 전파를 나타냅니다.얕은 물 θ > 20시간 동안 유효합니다.Bousinesq 단점은 Bousinesq 방정식이 KdV 방정식보다 풀기 어려운 경우가 많다는 것입니다.또한 많은 어플리케이션에서는 파동반사가 작기 때문에 무시될 수 있습니다. 공기파 Stokes의 파동 단, 장파에는 KdV 방정식에도 적용되는 Bousinesq 접근방식이 선호된다. 이는 얕은 물에서는 스토크스의 섭동 급수가 비선형 파형의 정점 과 길고 평평 한 기압골 때문에 솔루션을 향해 수렴하기 전에 많은 항을 필요로 하기 때문이다. KdV 또는 Bousinesq 모델은 이러한 긴 비선형 파형의 근사치를 제공합니다. KdV 방정식은 Bousinesq 방정식에서 도출할 수 있지만 전방파 전파를 분리하기 위해서는 추가적인 가정이 필요합니다. 실제 적용의 경우, KdV와 유사하지만 짧은 파장에서 훨씬 더 나은 주파수 분산 거동을 가진 전진 전파 모델인 KdV 방정식보다 벤자민-보나-마호니 방정식(BBM 방정식)이 선호된다. 단파 성능의 추가 개선은 보다 짧은 [4]
편파 타원 파라미터 m의 3가지 값에 대한 편파 프로파일. 파랑색 : m = 0, 빨간. : m = 0.9 및 블랙입니다. : m = 0.9999 。
KdV 방정식의 noidal 파동해는 1894년 [5] 1872년 Bousinesq 와 1876년 Rayleigh 에 의해 비선형 및 분산형 장파용 단독 파동이 발견되었다. 이러한 해법을 찾는 것은 자연과 실험실 [4] 고독 한 파동(또는 "번역의 파동")을 관찰함으로써 촉발되었다. KdV 방정식의 noidal 파동 해는 작은 [6]
수평 위치 x 및 시간 t의 함수로써, 편파(cnoidal wave)에 대한 표면 고도 θ (x ,t )는 다음과 같이 [7]
η ( x , t ) = η 2 + H cn 2 ( 2 K ( m ) x − c t λ m ) , \displaystyle \eta (x,t)=\eta _{2}+H,\operatorname {cn} ^{2},\leftflac\seta{array}{c}\displaystyle 2,K(m),{\frac {x-c,t}{\seta}},\m\end{array}},\right},},\,\,\,\,\,\,\,\,\,\,\cn} 여기 서 H는 파장 높이, θ 는 파장 , c 는 위상 속도, θ 는2 트로프 표고입니다.또한 cn은 야코비 타원함수 중 하나 이고 K(m )는 제1종의 완전한 타원적분 이다. 둘 다 타원 파라미터 m에 의존한다. 후자 m 은 편두파의 형태를 결정한다. m이 0일 경우 , 코사인 함수는 코사인 함수가 되고, 1에 가까운 값일 경우 코사인 함수는 피크 크레스트 와 (매우) 평탄한 트로프가 됩니다. m 값이 0.95보다 작을 경우 삼각함수를 사용하여 cnoidal 함수를 [8]
비선형 장파(δ δ h)의 중요한 무차원 파라미터는 Ursell 파라미터입니다.
U = H λ 2 h 3 = H h ( λ h ) 2 . {\displaystyle U=brac {H,\lambda ^{2}}{h^{3}}=brack {H}{h}},\left({\frac {h}}}\right)^{2}}. 예를 들어 U < [9] 작은 값에 대해서는 선형 이론을 사용할 수 있으며, 높은 값에서는 편파 이론과 같이 비선형 이론을 사용해야 한다. 3차 또는 5차 Stokes'와 편파 이론 사이의 경계 구역은 Ursell [10] Ursell 매개변수에 대한 공식에서 알 수 있듯이, 주어진 상대 파장 H /h에 대해 Ursell 매개변수와 비선형성은 상대 파장 δ /h 의 증가에 따라 빠르게 커집니다.
퍼텐셜 플로우 이론 내 에서의 표면 중력파의 완전한 비선형 문제의 해석에 근거해, 상기의 중심파는 섭동 계열의 최하위 항으로 간주할 수 있다.더 짧고 더 많은 비선형 파동에 대해서는 고차 노이드파 이론이 여전히 유효하다. 5차 뇌사상 파동 [11] Fenton의 [12]
크노이덜 파동의 설명은 재규격화를 통해 클라몬드에 [13] [14] 1994년 [15]
표면 장력 표면장력효과가 중요한 경우(또한) [16]
주기파 솔루션 코르테베그-드 브리스 방정식 Korteweg-de Vries 방정식(KdV 방정식)은 물파 및 치수 형태에 사용된다.[17]
∂ t η + g h ∂ x η + 3 2 g h η ∂ x η + 1 6 h 2 g h ∂ x 3 η = 0 , {\displaystyle _{t}\eta +{\tfrac {gh}\eta {x}\tfrac {3}{2}, {\tfrac {g}}\;\eta }, {x}\eta + {\tfrac {1}{6},\tfrac {2}, {\tfrac {\t}}}, {t}}, {t}, {g}}, {t}, {t}, {t}, {g}, {t}, {t}, {gh}, {g}, { 어디에
η : 표면 고도, x와 t 의 함수로, 양의 방향이 위로 향할 때(중력 상승), x : 수평 좌표, t : 시간, g : 지구 중력 의 값, h : 평균 수심 및 and와 x t : x 및 t에 관한 편도함수 연산자.
파생 상세
비차원화 중력 가속도 g와 수심 h를 사용하여 모든 양을 차원 없이 만들 수 있다.
η } = }}h style } display frac } h = x display style x = g t tilde { display frac frac KdV 방정식의[17]
∂ t ~ η ~ + ∂ x ~ η ~ + 3 2 η ~ ∂ x ~ η ~ + 1 6 ∂ x ~ 3 η ~ = 0 , {\displaystyle _{\tilde {t}}+\tilde {x}}{\tilde {t}}+{\tfrac {3}{\tilde {t}}, {\tilde {x}}, {\tfrac {t}}, {tfrac {t}}, {t}, {\t}}, {t} 나머지에서는 표기법을 쉽게 하기 위해 tildes 가 삭제됩니다.
표준 양식과의 관계 폼
∂ t ^ ϕ + 6 ϕ ∂ x ^ ϕ + ∂ x ^ 3 ϕ = 0 \displaystyle \hat {t}\phi +6,\phi \hat {x}\phi +\hat _{\hat {x}\phi = 0} 변환을 통해 얻을 수 있습니다.
t = 1 t display style hat = t = x t displaystyle } ϕϕ = 3 display phi twrac 3 t } 그러나 이 양식은 이 파생상품에서 더 이상 사용되지 않습니다.
고정 전파 위상속도 c로 이동 하는 주기파 해법을 모색한다.이러한 영구파는 다음과 같아야 합니다.
= ξ displaystyle \eta ) } displaystyle \ xi 파상 = displaystyle x c 따라서 공간과 시간과 관련된 부분파생상품은 다음과 같다.
x η ′ display display displaystyle x = ' 、 t t displaystyle c 、 여기서 denotes '은 인수 ξ에 대한 (())의 일반 도함수를 나타낸다.
이를 KdV 방정식으로 사용하여 다음과 같은 3차 상미분 방정식을 [18]
1 6 η ‴ + ( 1 − c ) η ′ + 3 2 η η ′ = 0. {\displaystyle {1}{6},\eta '+\left(1-c\right),\eta '+{\tfrac {3}{2}},\eta,\eta '=0.' 1차 상미분 방정식에 대한 적분 이 기능을 한 번 통합 하면 다음과 [18]
1 6 η ″ + ( 1 − c ) η + 3 4 η 2 = 1 4 r , {\displaystyle {1}{6}\eta '+\left(1-c\right),\eta +{\tfrac {3}{4}},\eta ^{2}=tfrac {1}{4}r,} r 적분 상수를 사용 합니다. 4를 곱한 후 다시 한 번 더[18]
1 3 ( η ′ ) 2 + 2 ( 1 − c ) η 2 + η 3 = r η + s , {\displaystyle {1}{3}}\left(\eta '\right)^{2}+2,\left(1-c\right),\eta ^{2}+\eta ^{3}=r,\eta +s,}, 를 다른 적분 상수로 설정 합니다. 이것은 양식에 기재되어 있습니다.
1 3 η ′ 2 = f η displaystyle tfrac } left = eta , f 3 2 c 1 2 r s display styleft tf teta ) (A )
세제곱 다항식 f(θ )는 θ 의 큰 양의 값에 대해 음이 되고, θ 의 큰 음의 값에 대해 양이 된다. 표면고도θ 는 실수값 이기 때문에 적분상수 r과 s 도 실수값이다.다항식 f는 그 근 θ1 , θ2 및 [7] θ 로3 나타낼 수 있다.
f ( η ) = − ( η − η 1 ) ( η − η 2 ) ( η − η 3 ) . \displaystyle f(\eta)=-\left(\eta -\eta _{1}\right),\left(\eta -\eta _{2}\right),\left(\eta -\eta _{3}\right) } (B )
f(θ )는 실수값이기 때문 에 3개의 루트 θ1 , θ 는2 3 모두 실수이거나, 그렇지 않으면 1개는 실수이고 나머지 2개는 복소공역쌍 이다. 후자의 경우, 실수치 루트가 1개뿐인 경우 f(θ )가 0인 표고 는 1개뿐 입니다. 그 결과 표면경사θ' 가 0인 표고 1개만 된다.그러나 우리는 표면 기울기가 0인 두 개의 표고(물리학) 를 가진 파도와 같은 솔루션을 찾고 있습니다. 결론은 f())의 세 근 모두 실제 가치가 있어야 한다는 것이다.
일반성의 손실 없이, 3개의 실제 루트는 다음과 같이 정렬된다고 가정합니다.
η 1 ≥ η 2 ≥ η 3 . \displaystyle \eta _{1}\geq \eta _{2}\geq \eta _{3}.,} 1차 상미분 방정식의 해 이제 등식(A θ )가 양 이면 기울기에 대한 실제 값만 존재한다는 것을 알 수 있습니다. 이것은 표면 표고가 진동하는 범위인 ηη 에2 1 대응합니다.f( η) 의 그래프도 참조해 주세요. 이 조건 은 다음과 같은 표고 표현으로 충족 됩니다.[7]
η ( ξ ) = η 1 왜냐하면 2 ψ ( ξ ) + η 2 죄 2 ψ ( ξ ) , \displaystyle \eta (\xi )=\eta _{1}\;\cos ^{2},\psi (\xi)+\eta _{2},\sin ^{2},\psi (\xi ) (C )
탐색된 파동 솔루션의 주기적 특성과 삼각함수 sin 및 cos의 위상 θ (θ )와 일치한다. 이 형식에서 등식 (A B
η − η 1 = − ( η 1 − η 2 ) 죄 2 ψ ( ξ ) , η − η 2 = + ( η 1 − η 2 ) 왜냐하면 2 ψ ( ξ ) , η − η 3 = ( η 1 − η 3 ) − ( η 1 − η 2 ) 죄 2 ψ ( ξ ) , 그리고. η ′ = − 2 ( η 1 − η 2 ) 죄 ψ ( ξ ) 왜냐하면 ψ ( ξ ) ψ ′ ( ξ ) 와 함께 ψ ′ ( ξ ) = d ψ ( ξ ) d ξ . {\displaystyle{\begin{정렬}\eta -\eta _{1}&, =-\left(\eta_{1}-\eta_{2}\right)\, \sin ^{2}\,\psi(\xi),\\\eta -\eta _{2}&, =+\left(\eta_{1}-\eta_{2}\right)\, \cos ^{2}\,\psi(\xi),\\\eta -\eta _{3}&, =\left(\eta_{1}-\eta_{3}\right)-\left(\eta_{1}-\eta_{2}\right)\, \sin ^{2}\,\psi(\xi),&,&{\text{과}}\\\eta '&, =-2\,\left(.\eta _{1}-\eta _{2}\righ t)\;\sin \psi (\xi )\cos \psi (\xi )\;\psi '(\xi )&{\text{d}\psi (\xi)}\cos \psi ' (\xi ) = sin frac {\text{d}\psi (\xi )\xi }. \end { aligned}} 식 (A B [7] θ 와 θ 에 관한 다음과 같은 상미분 방정식을 구한다.
4 3 ( d ψ d ξ ) 2 = ( η 1 − η 3 ) − ( η 1 − η 2 ) 죄 2 ψ ( ξ ) , {{displaystyle {{frac {4}{3}},\left\frac {\text{d}}\xi }}\right}^{2}=\left(\eta _1}-\eta _{3}\right)-left(\eta _1}-\eta _{2}\right)\sin(\xi) 오른쪽이 여전히 양수이므로, θ1 - η3 - η1 2 。일반성의 손실 없이, f ())는 구간 θ2 < no < η1 so so can can [7] with with with with with with with with with with with with with with with with with with with with with with with with with with with in in with with with with with with with in in zeros zeros
1 Δ d ξ d ψ = ± 1 1 − m 죄 2 ψ , {\displaystyle {\frac {1}{\Delta }}, {\frac {\text{d}}\psi }}=\pm, {\frac {1}{\fracrt {1-m\sin ^{2},\psi }}}, 포함:
δ 2 4 3 1 1 3 displaystyle Delta spec frac \ frac 、 m 1 1 1 η m fraceta fraceta } _ 여기 서 m은 0 µm µ1을 만족 시키는 이른바 타원 [19] [20] m3 µ12 1 "이기 때문입니다).파형 파고 에서 ξ = 0을 선택한 경우 = η1 통합은[7]
ξ = ± Δ ∫ 0 ψ d ψ ^ 1 − m 죄 2 ψ ^ = ± Δ F ( ψ m ) , \displaystyle \xi =\pm,\Delta \int _{0}^{\psi }{\hat {1-m},\sin ^{2}{\hat {psi }} =\pm,\Delta =F(psi }) (D )
첫 번째 종류의 불완전한 타원 적분 인 F( m m )를 사용 한다. 야코비 타원 함수 cn과 sn은 다음과 같이 주어진 F(θ m)의 역수이다.
왜냐하면 ψ)cn(ξ Δ m){\displaystyle\cos\,\psi =\operatorname{cn}\left({\begin{배열}{cc}\displaystyle{\frac{\xi}{\Delta}}&m\end{배열}}\right)}와 속죄제 ψ){\displaystyle\sin\,\psi =\operatorname{sn}\left({\begin{배열}{cc}\displaystyle{\frac{\xi}{\Delta(ξ Δ m)sn.}}& m\end {array}}\right). } 방정식(C [7]
η ( ξ ) = η 2 + ( η 1 − η 2 ) cn 2 ( ξ Δ m ) . (\displaystyle \eta (\xi )=\eta _{2}+\left (\eta _{1}-\eta _{2}\right),\operatorname {cn}^{2}\leftswarray{c}\displaystyle {frac {xi}{\delta }}}\m\end{array}\right}. } 이제 파라미터1 ,, ,, δ2 및 m 을 결정합니다.
cnoidal-wave 파라미터 간의 관계 첫째, θ 는1 파고이고 θ 는2 트로프 표고이므로 H = θ1 - θ 로2 정의 된 파고 를 도입하는 것이 편리하다. 따라서 m과 δ 에 대해 다음 과 같이 구한다.
m = H 1 η displaystyle flac H eta _ } 2 m = 4 3 displaystyle Delta frac 4 3 H}}} δ = 3 m H . displaystyle Delta rt frac 4 frac m H}}}}}}}. 중파 용액은 다음과 같이 쓸 수 있습니다.
η ( ξ ) = η 2 + H cn 2 ( ξ Δ m ) . {\displaystyle \eta (\xi )=\eta _{2}+H,\operatorname {cn}^{2}\leftflac\delta }{\delta }}\displaystyle {array}\m\end{array}\right. } 둘째, 트로프는 ψ = , , ,에 위치하므로 and = 0 과 ½ = ½ is is 사이의 거리는 식(D λ 로 한다.
1 2 µ 1 µ = δ m displaystyle { tfrac {1} {2} , \ displayda = \ Delta , F \ left ( { \ begin { array } { c } { \ tfright } { \ tfrac { } = right ) \Delta K (m ), giving = 3 K = 16 3 H K m displaystyle displayda Delta K sqrt frac 16 } frac m H}}}}\;K(m),} 여기 서 K(m )는 첫 번째 종류의 완전한 타원 적분 이다.셋째, 파동은 평균 수심 주변에서 진동하기 때문에 θ (θ)의 평균값은 0이어야 합니다. 그래서[7]
0 = ∫ 0 λ η ( ξ ) d ξ = 2 ∫ 0 1 2 λ [ η 2 + ( η 1 − η 2 ) cn 2 ( ξ Δ m ) ] d ξ = 2 ∫ 0 1 2 π [ η 2 + ( η 1 − η 2 ) 왜냐하면 2 ψ ] d ξ d ψ d ψ = 2 Δ ∫ 0 1 2 π η 1 − ( η 1 − η 2 ) 죄 2 ψ 1 − m 죄 2 ψ d ψ = 2 Δ ∫ 0 1 2 π η 1 − m ( η 1 − η 3 ) 죄 2 ψ 1 − m 죄 2 ψ d ψ = 2 Δ ∫ 0 1 2 π [ η 3 1 − m 죄 2 ψ + ( η 1 − η 3 ) 1 − m 죄 2 ψ ] d ψ = 2 Δ [ η 3 K ( m ) + ( η 1 − η 3 ) E ( m ) ] = 2 Δ [ η 3 K ( m ) + H m E ( m ) ] , {\displaystyle {text {aligned} 0&=int _{0}^{\text {d}\xi =2,\int _{0}^{{\tfrac {1}{2}\left[\eta _{1}-eta _2}\oper right] ;{\text{d}}\xi \\&, =2\,\int _{0}^{{\tfrac{1}{2}}\pi}{\Bigl[}\eta_{2}+\left(\eta_{1}-\eta_{2}\right)\,\cos^{2}\,\psi{\Bigr]}\,{\frac{{\text{d}}\xi}{{\text{d}}\psi}}\;{\text{d}}\psi=2\,\Delta \,\int _{0}^{{\tfrac{1}{2}}\pi}{\frac{\eta_{1}(\eta_{1}-\eta_{2}\right)\,\sin ^{2}\,\psi}{\sqrt{1-m\,\sin ^{2}\,\psi}}}\,{\text{d}}\p si \\&=2,\Delta,\int _{0}^{\tfrac {1}{2}\pi }{\frac {1}-m,\left(\eta _{1}-\eta _{3}\right),\sin ^2},\sin {\psi} } } } } ;{\text{d}}\psi \&=2,\Delta,{\Bigl [}\eta _{3},K(m)+\left(\eta _{1}-\eta _{3}\오른쪽), E(m){\Bigr }=2,\Delta 、 {\Lta } {3} 여기 서 E(m )는 두 번째 종류의 완전한 타원 적분 이다.타원 파라미터 m과 파고 H의 함수로서 θ1 , θ2 , θ 에3 대한 다음 식들이 [7]
3 = m m m displaystyle eta _ frac E m K 1 = H m 1 E K style 1 style \eta _{2}=squalfrac {H}{m},\left(1-m-{\frac {E(m)}{K(m)}}}\right). } 넷째, 식 (A B 위상속도 c와 루트 θ1 , θ2 , [7] θ 와의3 관계를 성립시킬 수 있다.
c = 1 + 1 2 ( η 1 + η 2 + η 3 ) = 1 + H m ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) . \displaystyle c=1+{\tfrac {1}{2},\left(\eta _{1}+\eta _{3}\right)=1+{\frac {H}{m},\left(1-{\frac {1}{2}}{2}},m-{frac},\frac {{}},\frac}{{frac},\frac},\frac},{{{frac},\frac}{frac}{frac},\frac},\frac}{{{{{{ } 상대 위상 속도 변화는 아래 그림에 나와 있습니다. 알 수 있듯이 m > 0.96(1 - m < 0.04)의 경우 파고가 높아짐에 따라 위상속도가 증가합니다. 이는 더 길고 더 많은 비선형 파동에 해당합니다. 고정 m에 대한 위상 속도의 비선형 변화는 파형 높이 H에 비례합니다. 위상 속도 c는 다음과 같이 파장 θ 및 주기 θ 와 관련이 있습니다.
c = λ τ . (\displaystyle c=syslogfrac {\displaystyle}) } 솔루션의 이력서 여기서의 모든 수량은 비차원화 이전의 표면 중력파에 유효 하게 치수 형태로 주어진다.
korteweg-de Vries 방정식에 대한 타원 매개변수를 m 으로 한 상대 위상 속도 증가 .수평 축은 10 ~ 100 =1 범위의 로그 −6 눈금을 사용합니다. 이 그림은 비차원적인 수량, 즉 위상속도 c를 얕은 물 위상속도 g h 파고 h 수심 h로 차원화하지 않는 수치이다. KdV 방정식의 noidal-fave 해는 다음과 같다.[7]
η ( x , t ) = η 2 + H cn 2 ( x − c t Δ m ) , {\displaystyle \eta (x,t)=\eta _{2}+H,\operatorname {cn}^{2}\leftflac\tarray}{c}\displaystyle {\frac {x-c,t}{\Delta }}\m\end{array}}\right}, 파고 가 H일 경우 - 파고 와 트로프 표고 간 의 차이2 , § 트로프 표고 , m 타원 매개변수 , c 위상 속도 및 Jacobi 타원 함수 중 하나.수조 레벨 δ2 및 폭 파라미터 δ 는 H, h 및 [7] m 으로 나타낼 수 있습니다.
2 H 1 m E m K displaystyle eta _ specfrac H m left frac K ( m and h 2 K m H}}}}}},} K (m )는 제1종의 완전한 타원 적분 이고 E (m )는 제2종의 완전한 타원 적분 이다.여기서 K(m )와 E(m )는 m = k 인2 타원 계수 k의 함수가 아닌 타원 매개변수 m의 함수로 표시 된다.
파장 θ , 위상속도 c 및 파동주기 θ 는 다음과 같이 H, h, m 에 관련 된다.[7]
§ = h 16 3 m H K {\displaystyle \displayda = h , {\displayrt {{\frac {16}{ 3}}{\frac {m, h}}{\frac {m,h}}{\displaystyle\frac {m ,h}}}{ H}}}\;K(m),} = g h 1 H h 1 2 m 3 2 m K m ]{ display style scrt gh left 1 frac } h} lefrac 2 } 지구의 중력 과 함께 .
대부분의 경우 알려진 파동 파라미터는 파고 H, 평균 수심 h, 중력가속도 g, 파장 θ 또는 주기 θ 이다. 그리고 위의 θ , c , θ 에 대한 관계를 이용하여 타원 파라미터 m을 구한다. 이것은 몇 가지 반복적 인 [3] 수치 해법을 필요 로 한다.
벤자민-보나-마호니 방정식 Benjamin-Bona-Mahony 방정식(BBM 방정식) 또는 정규화 장파(RLW) 방정식은 다음 과 [21]
∂ t η + g h ∂ x η + 3 2 g h η ∂ x η − 1 6 h 2 ∂ t ∂ x 2 η = 0. \displaystyle _{t}\eta +{\displayrt {g,h}},\displayrt {x}\eta +{\tfrac {3}{2},{\tfrac {g}{h}},\eta },\eta _{x},\displaystyle {\tfrac {g} {g}, {g}, {g}, {g}, {g}, {t}, {t}, {t}, {t}, {t} } 모든 수량은 KdV 방정식과 동일한 의미를 가집니다. BBM 방정식은 단파 [21]
파생 상세
파생 유도법은 KdV [22] 무차원 BBM 방정식은 평균 수심 h와 중력 가속도 [21]
∂ t η + ∂ x η + 3 2 η ∂ x η − 1 6 ∂ t ∂ x 2 η = 0. \displaystyle _{t}\eta +{x}\eta +{\tfrac {3}{2},\eta \tfrac {1}{6},\tfrac _{t},\tfrac _{2}\eta = 0. } 이것은 표준 형태로 가져올 수 있다.
∂ t ^ φ + ∂ x ^ φ + φ ∂ x ^ φ − ∂ t ^ ∂ x ^ 2 φ = 0 \displaystyle _{\hat {t}}\varphi +\display _{\hat {x}}\varphi +\varphi \,\display _{\hat {x},\display _{\hat {t},\display _{\hat {x}}\varphi =0} 다음과 같은 이점을 얻을 수 있습니다.
t = 6 、 displaystyle { scarrt 6 t = x scarrt 6 x φφφ = 3 x 、 displaystyle varphi sc frac eta 그러나 이 표준 양식은 여기서는 사용되지 않습니다.
KdV 방정식에 대한 노이다르 파동의 유도와 유사하게, θ = x-ct 인 주기파 용액 θ (θ )를 고려하면, BBM 방정식은 3차 상미분 방정식이 되며, 두 번 적분하여 다음을 얻는다.
1 3 η ′ 2 = f η η f display style tfrac = + 3 1 η r display eta = ^3 이것은 왼쪽의 (′)) 2 앞 에 있는 계수 c를 통해 KdV 방정식에 대한 방정식과는 다를 뿐이다. 좌표변환β = δ / displaystyle \scriptstyle c}} 단, 여기서는 앞의 방정식에 제시된 형식을 사용한다. 그 결과, KdV 방정식에서 발견된 것 과 같은 δ에 대한 공식은 다릅니다.
Δ = 4 3 m c H . {\displaystyle \Delta = scsrt {\frac {4}{3}}{\frac {m,c}{ H}}}}}}}. 파장 δ 의 관계는 H 와 m 의 함수로서 .\ displaystyle Delta
λ = 16 3 m c H K ( m ) . \displaystyle \displayda = displayrt {\frac {16}{3}}, {\frac {m,c}{ H}}}}\;K(m). } 나머지 부분에서는 KdV 방정식의 도출과 유사하며 여기서 반복되지 않습니다.
이력서 그 결과는 깊이 h의 유체 층의 물파에 대한 치수 형태로 제시된다.
매개변수에 대한 관련 관계와 함께 BBM 방정식의 noidal 파동 해는 다음과 같습니다.[22]
η ( x , t ) = η 2 + H cn 2 ( x − c t Δ m ) , η 2 = H m ( 1 − m − E ( m ) K ( m ) ) , Δ = h 4 3 m h H c g h = λ 2 K ( m ) , λ = h 16 3 m h H c g h K ( m ) , c = g h [ 1 + H m h ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) ] 그리고. τ = λ c . {\displaystyle {x,t}\eta _{2}+H,\operatorname {cn}^{2}\leftflac\tarray}{c}\displaystyle {x-c,t}{\Delta}}}}\m\end{array}\\\\mAC {2}&H} H}},{\frac {c}{\frac rt {g,h}}}&=frac {{2,K(m)}},\lambda &=h,{\frac rt {{\frac {16}},{\frac {m,h}}{\frac {m,h}}}}} H}},{\frac {c}{\fracrt {gh}}},\c&=fracsqrt {gh}},\left[1+{\frac {H}{m,h}},\left(1-{\frac {1}{2}},m-{\frac {2}},{frac}}{frac {gh}}}}}},{frac{frc}}}}},\frac {gh}}}}}},\frac {gh(m(m(m}) \end { aligned}} KdV 방정식의 중성파 용액과의 유일한 차이는 파장 [22] θ 에 대한 방정식이다. 실제 적용의 경우 일반적으로 수심 h, 파고 H , 중력 가속도 g 및 파장 θ 또는 가장 자주 주기(물리학) θ 가 제공된다. 그런 다음 위의 θ , c , θ 에 대한 관계에서 [3] 몇 가지 반복법을 통해 타원 파라미터 m을 구해야 한다.
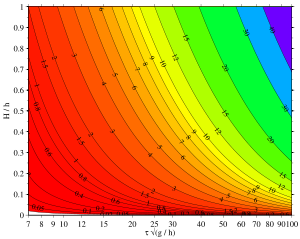
예 Korteweg-de Vries 방정식의 노이드 파동 솔루션에 대한 매개변수 관계. -log10 (1-m)는 완전한 타원 [20] 주기θg /h 상대파고H h 의 함수로 나타낸 것이다. 등고선을 따른 값은 -log10 (1-m)이므로, 값 1 은 m = 1 - 10−1 = 0.9, 값 40 은 m = 1 - 10이다−40 . 이 예에서는 Korteweg-de Vries(KdV) 방정식에 따른 노이드파가 고려된다. 파형의 파라미터는 다음과 같습니다.
평균 수심 h = 5m(16ft), 파도 높이 H = 3m(9.8ft),파동 주기 = 7초 ,중력 가속도 g = 9.81m/s2 (32ft/s2 ).그 이외의 경우에는 주기 θ 대신에 미리 알려진 양 으로 파장 θ가 발생할 수 있다.
첫째, 무차원 기간이 계산됩니다.
τ g h = 9.80 , {\displaystyle \displayrt {\frac {g} {h}} = 9.80,} 7개보다 크니까 동족상잔 이론이 타당할 정도로 길죠 알 수 없는 주요 항목은 타원 매개변수 m입니다. 이는 KdV 방정식에 대한 뇌파 이론에서 계산한 파동 주기 θ 가 다음과 같이 결정되도록 해야 한다.
§ = h 16 3 m H K {\displaystyle \displayda = h , {\displayrt {{\frac {16}{ 3}}{\frac {m, h}}{\frac {m,h}}{\displaystyle\frac {m ,h}}}{ H}}}\;K(m),} = g h 1 H h 1 2 m 3 2 m K m ]{ display style scrt gh left 1 frac } h} lefrac 2 } 는 주어진 값인 θ 와 일치합니다.여기서 θ 는 파장 이고 c는 파장의 위상 속도입니다. 또한 K(m ) 및 E (m )는 각각 제1종 및 제2종의 완전 타원 적분 이다.타원 파라미터 m의 검색은 시행착오 또는 수치근 탐색 알고리즘을 사용하여 수행할 수 있습니다. 이 init 경우, 최초 추측 m = 0.99부터 시작하여 시행착오를 통해 정답을 구합니다.
m = 0.9832 mdisplaystyle m=0.9832}) 검출되었습니다. 프로세스 내에서 파장 θ 및 위상 속도 c가 계산되었습니다.
파장 = 50 .8 m (140 ft) 및 위상속도 c = 7.26 m/s (23.8 ft/s)위상속도 c는 얕은 물 방정식에 따라 값 g (\ displaystyle\scriptstyle\sqrt {gh})
c g h = 1.0376 , {\ {g {\displaystyle {c} {\displayrt {g,h} = 1.0376,} 비선형 진폭 분산 효과로 인해 3.8% 증가를 나타내며, 이 경우 주파수 분산에 의한 위상 속도 감소에서 승리합니다.
이제 파장이 알려졌으므로 Ursell 번호도 계산할 수 있습니다.
U = H λ 2 h 3 = 62 , U {}} ,} {\displaystyle U=blambda ^{2}} = 62,} 그것은 작지 않기 때문에 선형파 이론은 적용되지 않지만, 중파 이론은 적용된다. 마지막으로 파장 대 심도의 비율이 θ / h = 10.2 > 7이므로 이 파장은 편파라고 볼 수 있을 정도로 길다.
매우 긴 비선형 파형의 경우 매개변수 m이 1에 가까운 m → 1일 때 야코비 타원 함수 cn은 다음과 같이 근사할[23]
cn z sech z 1 m )[ sinh ] z z sech ( ) display operatorname cn left z m ( tac sech 1 cosh z operatorname {sech } (z) = sech frac {1}{\cosh(z)} 。 } 여기서 sinh, cosh, tanh 및 sech는 쌍곡선 함수입니다. 제한 m = 1:
cn ) z m ) → ) z ) , \ m \displaystyle \operatorname {cn} \left(z m\right)\에서 \operatorname {sech}(z), sech(z ) = 1 / cosh(z )일 때.
또, 같은 한계 m→1에 대해서, 제1종 K(m)의 완전한 타원 적분은 무한대가 되고, 제2종 E (m )의 완전한 타원 적분은 [24] 이는 위상속도 c와 최소엘레벨레이션θ 의2 제한값이 다음과 같이 [25]
c = g h 1 2 H h ){ displaystyle sqrt {g,h }},\left(1+{\frac {1}{2}{2}}}, \, = 0 .\ display \eta {2 0,}}. 따라서 폭 파라미터 δ 의 관점에서 KdV 방정식과 BBM 방정식 모두에 대한 단독파해 는 다음과 같다.[25]
η ) x , t ) = H 2 ) x − c t Δ ) . \displaystyle \eta (x,t)=H,\operatorname {sech}^{2}\leftfrac {x-c,t}{\Delta }}\delta }\delta. } 중심파에 대해 발견되었으며 한계 m → 1에 있는 폭 매개변수는 KdV와 BBM [25]
Δ = h 4 h 3 H displaystyle\Delta=h,\frac{4,h}{ 3}H}}}}}}}: 및 : KdV 정정 : 。 Δ = h 4 h 3 H c g h }{displaystyle \Delta =h,{\frac { 4,h}{3 }H}},{\frac {c}{\sqrt {g,h}}}}}}}}}}: 방정식 BBM ★★★★
그러나 두 방정식의 단파 위상 속도는 높이 H와 깊이 H의 특정 조합에 대해 동일합니다.
극소 파고의 경우 긴 파도의 한계인 공기파 이론의 결과로 수렴될 것으로 예상 되며, 우선 극소 파고의 표면고도와 그 후 위상속도를 조사한다.
고도 ★★★★★★
야코비 타원 함수 cn은 푸리에 [26] 급수 로 확장될 수 있다.
cn ) z m ) = π m K ) m ) ∑ n = 0 ∞ ) ) 2 n + 1 ) π K ′ ) m ) 2 K ) m ) ) cos (cos) ) ) 2 n + 1 ) π z 2 K ) m ) ) . \displaystyle \operatorname {cn}(z m)=pi frac {\pi },K(m)},\sum _{n=0}^{\infty},\operatorname {sech} \left(2n+1),{\frac {pi },K(m}, {\m}. } K'( m )는 허수 사분기로 알려져 있고, K (m )는 야코비 타원 함수의 실사분기로도 불린다.이들은 K'(m ) = K(1-m)[27]
여기서의 관심은 작은 파라미터 m ≤ 1에 해당하는 작은 파고에 관한 것이므로, 완전 한 타원 적분 K 와 [28] [29] Maclaurin 시리즈 를 고려하는 것이 편리하다.
K ) m ) = π 2 1 + ) 1 2 ) 2 m + ) 1 ⋅ 3 2 ⋅ 4 ) 2 m 2 + ) 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ) 2 m 3 + ⋯ , E ) m ) = π 2 1 − ) 1 2 ) 2 m 1 − ) 1 ⋅ 3 2 ⋅ 4 ) 2 m 2 3 − ) 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ) 2 m 3 5 − ⋯ . {\displaystyle{\begin{정렬}(m)&, ={\frac{\pi}{2}}\,\left[1+\left({\frac{1}{2}}\right)^{2}\,m+\left({\frac{1\,\cdot \,3}{2\,\cdot \,4}}\right)^{2}\,m^{2}+\left({\frac{1\,\cdot \,3\,\cdot \,5}{2\,\cdot \,4\,\cdot \,6}}\right)^{2}\,m^{3}+\cdots \right],\\E(m)&, ={\frac{\pi}{2}}\,\left는 경우에는 1-\left({\frac{1}{2}}\right)^{2}\,{\frac{m}{1}}-\.({을 떠나\f {\displaystyle{\begin{정렬}(m)&, ={\frac{\pi}{2}}\,\left[1+\left({\frac{1}{2}}\right)^{2}\,m+\left({\frac{1\,\cdot \,3}{2\,\cdot \,4}}\right)^{2}\,m^{2}+\left({\frac{1\,\cdot \,3\,\cdot \,5}{2\,\cdot \,4\,\cdot \,6}}\right)^{2}\,m^{3}+\cdots \right],\\E(m)&, ={\frac{\pi}{2}}경우에는 1-\left({\frac{1}{2}}\right)^{2}\,{\frac{m}{1}}-\.({을 떠 \,\left는.나\frac{ rac {1,\cdot {2,\right} {2},{\frac {m^{3}}-\leftfrac {1,\cdot {3,\cdot} {2,4,\cdot }}\ right ^2 ,\frac {m} {m end}} 정렬된 {\end} 그런 다음 푸리에 급수에 나타나는 쌍곡 코사인 항은 다음과 [26] 작은 m µ 1에 대해 확장할 수 있습니다.
sech ( 2 1 k ( K m 2 q n 1 display operatorname { sech } left 2n 1 frac pi K K right frac aystyle q = \exp \left pi \,{\frac {K'(m)}{K(m)}}\right. } nome q는 작은 [30]
q = m 16 + 8 ( m 16 ) 2 + 84 ( m 16 ) 3 + 992 ( m 16 ) 4 + ⋯ . {{displaystyle q=black {m}{16}+8,\leftflac {m}{8}\right)^{2}+84,\leftflac {m}{16}\right)^{3}+992,\flac {m}{16}\right)^4}+\cdots.cdots. 따라서 푸리에 급수에서 첫 번째 항의 진폭 은 다음과 같습니다.
n = 0 {{displaystyle n=0} 다음과 같습니다. π m K ( m ) 석고 ( π K ′ ( m ) 2 K ( m ) ) = 1 − 1 16 m − 9 16 m 2 + ⋯ , {\displaystyle {\frac {m},K(m)},\operatorname {sech},\left\frac {pi},K'(m)'{2,K(m)}},\right)=1-{\tfrac {1}{16},{\tfrac {16}},{m},{\frac9}},{m}},{m}}},{m}}},{m},},}},{m},},},},},{m}}}}}},{c}, n = 1 {\displaystyle n=1,} 다음과 같습니다. π m K ( m ) 석고 ( 3 π K ′ ( m ) 2 K ( m ) ) = 1 16 m + 1 32 m 2 + ⋯ , {\displaystyle {\frac {m},K(m)}},\operatorname {sech},\leftfrac {3,\pi},K'(m)}{2,K(m)}}}\right)=tfrac {1}{16},m+tfrac {32}}{,}}}}},{2,32},},}}},},},},},},},\frac},\frech. n = 2 {\displaystyle n=2,} 다음과 같습니다. π m K ( m ) 석고 ( 5 π K ′ ( m ) 2 K ( m ) ) = 1 256 m 2 + ⋯ . {\displaystyle {\frac {m},K(m)}},\operatorname {sech},\leftfrac {5,\pi},K'(m)},\right)=tfrac {1}{256},m^2}+cdots.
따라서 m ≤ 1의 경우 야코비 타원 함수는 첫 번째 푸리에 급수 항을 가집니다.
Cn(zm)=(1− 1에서 16m− 916m2+⋯)못 말리겠고α z+(1에서 16m+132m2+⋯). 왜냐하면 2α z+(1256m2+⋯). 왜냐하면 3α z+⋯,{\displaystyle{\begin{정렬}\operatorname{cn}\,(zm)&, ={\Bigl(}1-{\tfrac{1}{16}}년.,m-{ \tfrac {9}{16},m^{2}+\cdots&{\Bigr}\;\cos\,\alpha\ z\\\&+\;{\} Bigl(}{\tfrac {1}{16}},m+{\tfrac {1}{32},m^{2}+\cdots&{\Bigr})\;\cos \,2,\alpha \,z;\&+\;{\ Bigr}\;\cos \,\cos \cos \,\cdots\,\cdots\,\cdots\,\cdots\cdots\cdots\cdots\\ Bigl(}{\tfrac {1}{256},m^{2}+\cdots&{\Bigr})\;\cos ,\alpha\,z\;\cdots,\ end{ }( α k 2K).\displaystyle \equivfracpi({2}) } 그리고 사각형은
cn 2 ( z m ) = ( 1 2 − 1 16 m − 1 32 m 2 + ⋯ ) + ( 1 2 − 3 512 m 2 + ⋯ ) 왜냐하면 2 α z + ( 1 16 m + 1 32 m 2 + ⋯ ) 왜냐하면 4 α z + ( 3 512 m 2 + ⋯ ) 왜냐하면 6 α z + ⋯ . {\displaystyle {cn}\operatorname {cn}^{2},(z m)&=bigl (}{\tfrac {1}{16}-{\tfrac {1}{32},m^{2}+\cdots&{Bigr}\+{}\\\\tfrac {1}\{2}\tfrac {{1}\frac {1}}}\\\cdl}\{{{{{\}}}}}}}\cdots}\cdots}\cdots}\cdots Bigl(}{\tfrac {1}{2}}-{\tfrac {3}{512},m^{2}+\cdots&{\Bigr}\;\cos \,2,\alpha \,z;\&+;{\Bigr})\;\cos \,\cos \,\cos \,\cs\,\cdots\,\,\,\cdots\,\,\cs\cdots\cdots\cs\ Bigl(}{\tfrac {1}{16}},m+{\tfrac {1}{32},m^{2}+\cdots&{\Bigr})\;\cos \,4,\alpha \,z;\&+\;{\Bigr}\;\cos \,\cos \cos \,\cdots\,\cdots\,\cdots\,\cdots\cdots\\cdots\cdots\ Bigl(}{\tfrac {3}{512}},m^{2}+\cdots&{\Bigr}}\;\cos,6,\alpha,z\+\cdots.\end{aligned}}} 타원 파라미터 m의 작은 값에 대해 편파 자유표면θ (x ,t )는 푸리에 급수로 표현된다. 먼저 cn 함수의 인수는 δ /δ 이며 파장 = 2 δ K(m )이므로 다음과 같이 하십시오.
θ ≡ π ξ K ( m ) ξ Δ = 2 π ξ λ . \displaystyle \theta \equiv {K(m)}, {\frac {xi }}=2,\pi }, {\frac {xi }{\frac }, {\frac }, {\frac {xi }, {\frcda}}. } 또한 평균 자유면 표고는 0이다. 따라서 작은 진폭파의 표면 고도는
η ( x , t ) = H ( 1 2 − 3 512 m 2 + ⋯ ) 왜냐하면 θ + H ( 1 16 m + 1 32 m 2 + ⋯ ) 왜냐하면 2 θ + H ( 3 512 m 2 + ⋯ ) 왜냐하면 3 θ + ⋯ . \displaystyle \eta(x,t)=\; H,{\Bigl(}\tfrac {1}{2}}-{\tfrac {3}{512}},m^{2}+\cdots{Bigr},\cos,\theta \;+\; H,{\Bigl(}{\tfrac {1}{16}},m+{\tfrac {1}{32}},m^{2}+\cdots{Bigr},\cos \,2\theta \;+\;;;;;; H,{\Bigl(}{\tfrac {3}{512}},m^{2}+\cdots{Bigr}},\cos,3\theta\;\cdots.} 또 KdV방정식과 BBM방정식은 달리 파장θ 를 타원파라미터 m의 맥로린계수로 확장할 수 있지만 현시점에서는 그럴 필요가 없다.
참고 : 0m 에 대한 제한 동작(미소한 파고 높이에서)[31] cn ( z m ) ≈ 왜냐하면 ( z ) + 1 4 m ( z − 죄 ( z ) 왜냐하면 ( z ) ) 죄 ( z ) + ⋯ , \displaystyle \operatorname {cn} (z m)\about \cos(z)+{\tfrac {1}{4}},m,{\bigl (}z-\sin(z),\cos(z){\bigr},\sin(z)+\cdots}, 단 , 이 근사치 의 m 에 비례하는 고차항에는 cn(z m)의 주기 4K (m)와 코사인 cos(z)의 주기 2'의 불일치로 인해 영속항 이 포함되어 있습니다.작은 m에 대한 위의 푸리에 급수는 이러한 단점을 가지고 있지 않으며, 섭동 이론에서 린드슈테트-푸앵카레 방법 을 사용하여 발견된 형태와 일치한다.
극소 파고의 경우, 한계 m → 0에서 자유 표면 고도는 다음과 같이 됩니다.
xi x 12 H cos 、 displaystyle \eta t 2 xixi 2 = pi frac (\ displaystyle = frac } 따라서 파형의 진폭은 파고의 절반 인 µH입니다.이는 에어리파 이론에서 연구한 것과 같은 형태이지만, 중파 이론은 평균 수심보다 훨씬 긴 파장을 가진 긴 파장에 대해서만 유효하다는 점에 주목한다.
위상 속도 파생 상세
KdV 및 BBM 방정식의 경우 모두 중심파의 위상 속도는 다음과 같습니다.[7] [22]
c = g h [ 1 + H m h ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) ] . ({displaystyle c=carrt {gh},\left[1+{\frac {H}{m,h}},\left(1-{\frac {1}{2}},m-{\frac {E(m)}}}},{\frac {E(m)}}}},\right},\frac {\frac {\frac {\frac {\frac {\f},\frac {\f},\frac {\frac {\f},\frac {\f},\f},\}, } 이 공식에서 위상 속도는 파형 높이 H와 파라미터 m의 함수 입니다. 단, 극소 높이의 파동에 대한 전파를 결정하기 위해서는 파라미터 m이 0에 가까워지는 한계에서 일정한 파장 θ 에서의 위상 속도의 거동을 결정할 필요가 있다. 이것은 파장 방정식을 사용하여 실행할 [7] [22]
KdV: λ = h 16 3 m h H K ( m ) , \displaystyle \displayda = h, {\displayrt {{\frac {16}{3}}, {\frac {mh}{ H}}}}},K(m),} BBM: λ = h 16 3 m h H c g h K ( m ) , \displaystyle \displayda = h, {\displayrt {{\frac {16}{3}}, {\frac {mh}{ H}},{\frac {c}{\sqrt {g,h}}}}},K(m),}
상대 wavenumber µh 소개:
κ h = 2 π λ h , {\displaystyle \kappa \,h = pi frac {2,\pi }{\displayda }},h,} 상기의 위상속도 및 파장방정식을 이용하여 위상속도의 H /m계수 를 θh , m 으로 치환할 수 있다. 결과 위상 속도는 다음과 같습니다.
KdV: c = g h [ 1 + ( κ h ) 2 4 3 π 2 K 2 ( m ) ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) ] , {{displaystyle c=bgh},\left[1+(\kappa\h)^{2},{\frac {4}{3,\pi ^{2}},K^{2}(m),\left(1-{\frac {1}{2}},m-{\frac {2}},\frac(K}) {K} BBM: c = g h 1 1 − ( κ h ) 2 4 3 π 2 K 2 ( m ) ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) . {\displaystyle c=carcrt {gh},{\displaystyle 1-(\kappa\h)^{2},{\frac {4}{3,\pi ^{2}},K^{2}(m),\left(1-{\frac {2}},{\frac {2}},{\frac {2}},{{\fr}, {\fr}, {\frc}, {\fr}, {\fr} }
작은 m에 대한 제한 거동은 K(m )와 E(m )[28] 대한 Maclaurin 시리즈 를 사용하여 분석할 수 있으며, 그 결과 c에 대한 두 공식의 공통 인수에 대해 다음과 같은 식을 얻을 수 있다.
γ = 4 3 π 2 K 2 ( m ) ( 1 − 1 2 m − 3 2 E ( m ) K ( m ) ) = − 1 6 + 1 64 m 2 + 1 64 m 3 + ⋯ , {\displaystyle \frac {4}{3,\pi ^{2}},K^{2}(m),\left(1-{\frac {1}{2}},m-,{\frac {3}{2}},{\frac {E(m)}}{K(m}}}},\frac {\tac}{1}{{tac}}{2}}}{displaystylfrac} 그 한도에서 그래서 m→ 0, 인자 γ→−.mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1⁄6. m ≤ 1에 대한 위상 속도의 제한값은 직접 발생한다.
KdV 방정식과 BBM 방정식에 대한 noidal 파동 이론에 따르면, 극소 파고의 위상 속도는 다음 과[32]
KdV 다음과 같습니다. c = [ 1 − 1 6 ( κ h ) 2 ] g h , {{displaystyle c=bigl [}1-{\tfrac {1}{6}},\left(\kappa h\right)^{2}{\Bigr}},{\bigrt {g,h}}}}, BBM : c = 1 1 + 1 6 ( κ h ) 2 g h , {{displaystyle c=black {1}{6},\left(\kappa h\right)^{2}},{\blackrt {g,h}},
κ = 2 / / λ wavenumber 및 κ h 상대 wavenumber입니다.이러한 위상 속도는 선형화된 KdV 및 BBM 방정식의 사인파 솔루션을 직접 검색하여 얻은 결과와 완전히 일치합니다. 이러한 방정식에서 알 수 있듯이 선형화된 BBM 방정식은 모든 µh 에 대해 양의 위상 속도를 가집니다. 한편, 선형화된 KdV 방정식의 위상속도는 단파에 대해 θh > 6(\ displaystyle\scriptstyle\sqrt{6
브라질 북동부 아라과리 강 하구 부근에 있는 물결 모양의 보어 . 약 100피트(30m)[33] 중성파는 비점성 , 비회전성 및 비압축성 흐름방정식에서 직접 도출할 수 있으며, Benjamin & Lightill( 1954)이 물결 의 세 가지 불변량으로 표현한다. 기준 프레임이 일정한 흐름 이 되는 위상 속도에 따라 이동하는 기준 프레임 에서 중심파 용액은 흐름의 질량 플럭스, 운동량 플럭스 및 에너지 헤드에 직접 관련지을 수 있다. Benjamin & Lightill( 1973)에 이어 (압축할 수 없는 흐름의 흐름 함수 설명을 사용하여) 유속의 수평 및 수직 구성요소는 흐름 함수 δ (θ ,z )의 공간적 도함수 z δ (θ = ξ x-ct )이다. 수직 좌표 z는 중력 가속도 방향과 반대인 위쪽 방향에서 양의 값이고 z 의 0 레벨은 유체 영역의 불투과 하한에 있습니다. 자유 표면은 z = (())에 있는 반면, is 는 국소 수심이며, 표면 표고 depth())와 관련 이 있으며 h 는 평균 수심이다.
이 정상류에서는 각 수직단면에서의 토출Q 가 θ 에 의존하지 않고 일정하며, 수평바닥에 의해 각 수직단면을 통과하는 수평운동량 플럭스S 를 밀도 θ 로 나눈 수평운동량 플럭스S도 보존된다. 또, 이 비점성 및 비회전성 흐름에 대해서는, 베르누이의 원리 를 적용할 수 있어 플로우 영역내의 어디에서나 같은 베르누이 상수 R을 가진다. 다음과 [34]
Q = ∫ 0 ζ ) ξ ) ∂ z Ψ d z , R = p ρ + 1 2 ) ∂ ξ Ψ ) 2 + ) ∂ z Ψ ) 2 + g z ... S = ∫ 0 ζ ) ξ ) p ρ + ) ∂ z Ψ ) 2 d z . _big(왼쪽 Q&=\int _{0}^{\zeta (\xi )}\psi _{z}\Psi \;{\text{d}}z,\R &=parcfrac {p}{\rho }}+{\tfrac {1}{ 2},{\Bigl [\xi }\xi} } } } } 。S&=\int _{0}^{\zeta (\xi )}\left [{\frac {p}{\rho }}+\left (\frac _{z}\Psi \right)^2}\right]\ ;{\text{d}}z. end {aligned} 상당히 긴 파장의 경우 파장 θ 에 비해 수심 θ 가 작다고 가정할 때 수심 θ (θ)와 세 가지 불변량 Q , R ,[34]
1 3 Q 2 ( ζ ′ ) 2 ≈ − g ζ 3 + 2 R ζ 2 − 2 S ζ + Q 2 . (\displaystyle { tfrac {1} {3} , Q^{2} , \left (\zeta '\right )^{2} \ about -g , \zeta ^{3} + 2,R , \zeta ^{2} \zeta + Q^{2} ) 。 } (E )
이 비선형 및 1차 상미분 방정식은 편파 해법을 가지고 있다.
깊이 h의 유체에 미세 한 진폭의 매우 긴 파동이 있고 흐름 속도 v가 균일한 경우 흐름 상수는 얕은 물 [34] 방정식 에 따른다.
Q = v display style Q h 0 = 2 v g h 2 h R 0 = tfrac {1} g h 0 = h 1 h ( display S } 방정식(E 방전 Q와 중력 가속도 g를 사용하여 임계 깊이c h를 정의함으로써 비차원 형태로 만들 수 있다.
h c = Q 2 g 3 , ({displaystyle h_{c}=sqrt[{3}]{\frac {Q^{2}}}{g}}}) 아임계 플로우와 초임계 플로우 사이의 임계 플로우 경계에 관련됩니다(「Froude 번호 」도 참조).따라서 방정식의 비차원 형태는 다음과 같다.
1 3 ( ζ ~ ′ ) 2 ≈ − ζ 3 + 2 R ~ ζ ~ 2 − 2 S ~ ζ ~ + 1 , {\displaystyle {tfrac {1}{3},\left({\tilde {\zeta }}^{3}+2,{\tilde {S},{\tilde {zeta}}+2,{\tilde {S}},{\tilde {zeta}+1,}}}\tilde {\tilde {\tele {\}},},\telde {{{{{\}}}}}},{\}}}}},{{\}}}}}}},{\}} 와 함께
= ζ h style tilde = fr frac c } c style } RG c style tilde } frac th _ c \tilde {S}}=flac {S}{g,h_{c}^{2}}. } 파생 먼저 베르누이 방정식을 사용하여 운동량 플럭스 S에서 압력 p를 제거합니다.
S = R ζ − 1 2 g ζ 2 + ∫ 0 ζ 1 2 [ ( ∂ z Ψ ) 2 − ( ∂ ξ Ψ ) 2 ] d z . {\displaystyle S=R,\zeta -{\tfrac {1}{2},g,\zeta ^{0}^{0}{\zeta}{\tfrac {1}{2}\left[\left(\tfrac _{z}\Psi \right)^2}-\left(\left(\tfright)^{{{{xi }{{2}{{{{2}{{\psi }\psi }\psi } } } } } } ;{\text{d}}z. } 흐름 함수 δ 는 z = 0에서 침대 주위 에 맥클라우린 계열로 확장되며, 불침투성 침대가 유선이고 흐름의 비회전성(Z = 0 에서 z 2 δ = 0):[34]
Ψ = z u b ( ξ ) − z 3 3 ! u b ″ ( ξ ) + z 5 5 ! u b iv ( ξ ) + ⋯ , {\displaystyle \Psi =z,u_{b}(\xi)-{\frac {z^{3}}}{3! },u_{b}(\xi)+{\frac {z^{5}}{5! },u_{b}^{\text{iv}}(\xi)+\cdots,} 바닥 z = 0의 수평 속도 에서b u. 파동이 h µ µ µ 길기 때문에 Q 와 S에 대한 근사치에서는 z와 µ 까지만3 유지 됩니다3 .그러면 운동량 플럭스 [34]
S = R ζ − 1 2 g ζ 2 + 1 2 ζ u b 2 − 1 6 ζ 3 u b u b ″ − 1 6 ζ 3 ( u b ′ ) 2 + ⋯ . {\displaystyle S=R,\zeta -{\tfrac {1}{2},g,\zeta ^{2}+{tfrac {1}{6},\zeta ^{3},u_{b},{b},{b},{b},{b},\zeta {frac} {} 방전 Q는 자유 표면 z = θ 에서의 스트림 함수 δ 값이기 때문에 다음과 같이 됩니다.
Q = ζ u b ( ξ ) − 1 6 ζ 3 u b ″ ξ + ⋯ . {\displaystyle Q=\zeta {b}(\xi)-{\tfrac {1}{6}},\zeta ^{3},u_{b}'{\xi }+\cdots.} 보시는 바와 같이 방전 Q는 O(θ )량입니다. 이로부터, 바닥 속도는 다음과[34]
u b = Q ζ + 1 6 ζ 2 u b ″ + ⋯ . {\displaystyle u_{b}=frac {Q}{\zeta}}+{\tfrac {1}{6}},\zeta ^{2},u_{b}'+\cdots.} Q / is 는 1개 주문 수량입니다.이 관계는 운동량 플럭스 S에서 침대 속 도b u를 Q와 θ 로 대체하기 위해 사용된다. 여기서 다음 용어를 얻을 수 있습니다.
u b 2 = Q 2 ζ 2 + 1 3 ζ Q u b ″ + ⋯ , u b ′ = − Q ζ ζ ′ + 1 3 ζ ζ ′ u b ″ + 1 6 ζ 2 u b ‴ + ⋯ 그리고. ( u b ′ ) 2 = Q 2 ζ 4 ( ζ ′ ) 2 − 2 3 Q ζ ζ ′ u b ″ + ⋯ . {\displaystyle{\begin{정렬}u_{b}^{2}&, ={\frac{Q^{2}}{\zeta ^{2}}}+{\tfrac{1}{3}}\,\zeta \,Q\,u_{b}"+\cdots ,\\u_{b}'&, =-{\frac{Q}{\zeta}}\,\zeta '+{\tfrac{1}{3}}\,\zeta\,\zeta '\,u_{b}"+{\tfrac{1}{6}}\,\zeta ^{2}\,u_{b}"'+\cdots({\text{과}}\\\left(u_{b}'\right)^{2}&, ={\frac{Q^{2}}{\zeta ^{4}}}\,\left(\zeta '\right)^{.2}-{\tfrac{ 2) {3}}, {\frac {Q}{\zeta }}, \zeta ',u_{b}'+\cdots.\end{aligned}} 그 결과 운동량 플럭스 S는 다시 [34] θ 에3 비례하는 항만을 유지한다.
S ≈ R ζ − 1 2 g ζ 2 + 1 2 Q 2 ζ − 1 6 Q 2 ζ ( ζ ′ ) 2 . {\displaystyle S\approx R,\zeta -{\tfrac {1}{2},g,\zeta ^{2}+{\tfrac {1}{2}},{\zeta},{\tfrac {1}{6},{\zeta}},{\tfrac {Q^{1},{1},{2},{2}}},\zeta},{{\zeta}, 이는 방정식(E)의 형태로 직접 재캐스팅할 수 있습니다.
퍼텐셜 잠재 에너지 밀도
E 냄비 = 1 λ ∫ 0 λ 1 2 ρ g η 2 ( x , t ) d x {\displaystyle E_{\text{pot}}=black {1}{\textda}},\int _{0}{\tfrac {1}{2},\rho \g,\eta ^{2}(x,t)\;\text{d}}x}, δ 유체 밀도 를 갖는 는 KdV [35] 불변수 중 하나이다.이것은 표면 표고θ(x ,t )에 KdV 방정식을 곱하면 알 수 있다. 체인 규칙 을 반복적으로 사용하면 다음과 같은 결과가 나온다.
∂ t ( 1 2 η 2 ) + ∂ x { 1 2 g h η 2 + 1 2 g h η 3 + 1 12 h 2 g h [ ∂ x 2 ( η 2 ) − 3 ( ∂ x η ) 2 ] } = 0 , {\displaystyle _{t}\leftfrac {1}{2}},\eta ^{2}\right_{x}\left\{\tfrac {1}{{\tfrac {1}{2},\eta ^{\tfrac {1}{2},\tfrac {1}{2},\tfrac} {{g}}},\rc},\t {{{g}, {g}}, {g}},\frac},\c} 보존 형태이며 주기성 간격(중파 파장)에 걸쳐 적분 후 불변이다. 퍼텐셜 에너지는 BBM 방정식의 불변수는 아니지만 δg [θ2 + 1µ62 h (x θ )]2 는 다음과 같습니다.[36]
우선, 동공파에서의 표면고도의 분산 을 산출한다. η2 = -(1/dc ) λ h H cn2 (dx ) dx, cn(dcn /dc) = cos ((dcs ) 및 λ = 2 Ω K(m )이므로[37]
1 λ ∫ 0 λ η 2 d x = 1 λ ∫ 0 λ { η 2 + H cn 2 ( ξ Δ m ) } 2 d ξ = H 2 λ ∫ 0 λ cn 4 ( ξ Δ m ) d ξ − η 2 2 = Δ H 2 λ ∫ 0 π 왜냐하면 4 ψ d ξ d ψ d ψ − η 2 2 = H 2 2 K ( m ) ∫ 0 π 왜냐하면 4 ψ 1 − m 죄 2 ψ d ψ − η 2 2 = 1 3 H 2 m 2 [ ( 2 − 5 m + 3 m 2 ) + ( 4 m − 2 ) E ( m ) K ( m ) ] − H 2 m 2 ( 1 − m − E ( m ) K ( m ) ) 2 {\displaystyle{\begin{정렬}{\frac{1}{\lambda}}\,\int _{0}^{\lambda}\eta ^{2}\,{\text{d}}x&, ={\frac{1}{\lambda}}_{0}^{\lambda}\left\{\eta_{2}+H\,\operatorname{cn}^ᆶ\left({\begin{배열}{cc}\displaystyle{\frac{\xi}{\Delta}}&m\end{배열}}\right)\right\}^{2}\ \int,{\text{d}}\xi ={\frac{H^{2}}{\lambda}}\int _{0}^{\lambda}\op.eratorna 나{cn}^ᆫ\left({\begin{배열}{cc}\displaystyle{\frac{\xi}{\Delta}}&m\end{배열}}\right)\,{\text{d}}\xi-\eta _{2}^{2}\\&, ={\frac{\Delta \,H^{2}}{\lambda}}\int _{0}^{\pi}\cos(\,{\frac{{\text{d}}\xi}{{\text{d}}\psi}}\;{\text{d}}\psi-\eta _{2}^{2}={\frac{H^{2}}{2\,K(m)}}\int _{0}^{\pi}{\frac{\cos ^{4}\,\psi}{\sqrt. {1-m\,\s (^{2},\psi }}\;{\text{d}}\psi -\eta _{2}^{2}\\&=frac {H^{1}{3},{\frac {{2}},\left[\left(2-5,m+3,m^2}\right)+{2},{2},\,\frac {\frac {\frac{2}},\frac {\frac{{2}},\fright},\fright},{{{{{{{2}},\f},\f},\f}, KdV와 BBM 방정식 모두에 대한 잠재적 에너지는 다음과[37]
E 냄비 = 1 2 ρ g H 2 [ − 1 3 m + 2 3 m ( 1 + 1 m ) ( 1 − E ( m ) K ( m ) ) − 1 m 2 ( 1 − E ( m ) K ( m ) ) 2 ] . {\displaystyle E_{\text{pot}}=tfrac {1}{2}},\rho,g, H^{2},\left [-{\frac {1}{3,m}}+{\frac {2}{3,m}},\left(1+{\frac {1}{m}\right)\left(1-{\frac {E(m)}}}}{K(m}}}}}\right-{\frac {\frac {{{{{\frac}}}}}}}}}{{\frac {\frac1}{{{{\fright}}}}}}}}}}}{{{\fright}}}} } 퍼텐셜 에너지의 극소 파장 높이 한계(m → 0)는pot E 1µ16µg2 H로 에어리 파장 [37] 이론 과 일치합니다. 파형 높이는 진폭의 두 배 인 H = 2a이며, 극소 파동 한계치입니다.
「 」를 참조해 주세요. 주 및 참고 자료 메모들 ^ Nezlin, M.V. (1993), Physics of intense beams in plasmas , CRC Press, p. 205, ISBN 978-0-7503-0186-2 ^ Le Méhauté, B. (1976), An introduction to hydrodynamics and water waves , Springer, ISBN 978-0-387-07232-6 ^ a b c 딩게만스(1997) 페이지 718-721. ^ a b 딩게만스(1997) 페이지 689-691. ^ de Jager, E.M. (2006). "On the origin of the Korteweg–de Vries equation". arXiv :math/0602661v1 ^ Drazin, P.G. (1977), "On the stability of cnoidal waves", Quarterly Journal of Mechanics and Applied Mathematics , 30 (1): 91–105, doi :10.1093/qjmam/30.1.91 ^ a b c d e f g h i j k l m n o 딩게만스(1997) 페이지 708-715. ^ Yunfeng Xu; Xiaohe Xia; Jianhua Wang (2012), "Calculation and approximation of the cnoidal function in cnoidal wave theory", Computers & Fluids , 68 : 244–247, doi :10.1016/j.compfluid.2012.07.012 ^ Ursell 파라미터는 U 32 32 / / 3 1002 100일 때 선형 이론이 적용됨을 나타냅니다.^ Sorensen, R.M. (1993), Basic wave mechanics: for coastal and ocean engineers , Wiley-Interscience, ISBN 978-0-471-55165-2 , 페이지 61.^ Fenton, J.D. (1979), "A high-order cnoidal wave theory", Journal of Fluid Mechanics , 94 (1): 129–161, Bibcode :1979JFM....94..129F , doi :10.1017/S0022112079000975 ^ Fenton, J.D. (1990), "Nonlinear wave theories", in Le Méhauté, B.; Hanes, D.M. (eds.), Ocean Engineering Science , The Sea, vol. 9A, Wiley Interscience, pp. 3–25 ^ Clamond, D. (1999), "Steady finite-amplitude waves on a horizontal seabed of arbitrary depth", Journal of Fluid Mechanics , 398 (1): 45–60, Bibcode :1999JFM...398...45C , doi :10.1017/S0022112099006151 ^ Clamond, D. (2003), "Cnoidal-type surface waves in deep water", Journal of Fluid Mechanics , 489 : 101–120, Bibcode :2003JFM...489..101C , CiteSeerX 10.1.1.573.3434 doi :10.1017/S0022112003005111 ^ Osborne, A.R. (1994), "Shallow water cnoidal wave interactions" (PDF) , Nonlinear Processes in Geophysics , 1 (4): 241–251, doi :10.5194/npg-1-241-1994 ^ Vanden-Broeck, J.-M.; Shen, M.C. (1983), "A note on solitary and cnoidal waves with surface tension", Zeitschrift für angewandte Mathematik und Physik , 34 : 112–117, doi :10.1007/BF00962619 , S2CID 119997409 ^ a b 딩게만스(1997) 페이지 692-693. ^ a b c 딩게만스(1997) 페이지 701 ^ 아브라모위츠 & 스테건(1965) 페이지 590 ^ a b 타원 모수 m은 타원 계수 k: m = k 와2 구별됩니다. Abramowitz & Stegun(1965) 페이지 590 참조. ^ a b c 딩게만스(1997) 페이지 694-696. ^ a b c d e 딩게만스(1997) 페이지 715 ^ 아브라모위츠 & 스테건(1965년) Eq. 16.15.2, 페이지 574. ^ Abramowitz & Stegun (1965) 그림 17.1 및 17.2, 592 페이지 ^ a b c 딩게만스(1997) 페이지 702-704. ^ a b 아브라모위츠 & 스테건(1965년) Eq. 16.23.2, 페이지 575 ^ 아브라모위츠 & 스테건(1965년) Eq. 17.3.5, 590페이지 ^ a b 딩게만스(1997) 페이지 784. ^ 아브라모위츠 & 스테건(1965년) Eqs. 17.3.9 및 17.3.10, 페이지 591 ^ 아브라모위츠 & 스테건(1965) 17.3.21, 페이지 591. ^ 아브라모위츠 & 스테건(1965) Eq. 16.13.2, 페이지 573. ^ 딩게만스(1997) 페이지 695 ^ 그림 5 in: ^ a b c d e f g Benjamin & Lightill (1954) ^ 딩게만스(1997) 페이지 730-733. ^ Benjamin, Bona & Mahony (1972) ^ a b c 딩게만스(1997) 페이지 791-794. 레퍼런스 아브 밀턴, Stegun, Irene은 앤, eds.(1983년)[6월 1964년]."16장.야코비 타원 함수고 세타 functions".Formulas, Graphs,과 수학적 표로 핸드 북 수학의 함수입니다.응용 수학 시리즈이다.Vol55(10원래 인쇄의 추가로 수정 작업과 교정을 9재판(1972년 12월) 제1판).워싱턴 DC, 뉴욕:미국 상무부, 표준국의 도버 출판사.를 대신하여 서명함. 제567절, 587. 아이 에스비엔 978-0-486-61272-0. LCCN 64-60036.MR0167642.LCCN 65-12253.장 17참조하십시오. 타원 적분 .Benjamin, T.B. ; Bona, J.L. ; Mahony, J.J. (1972), "Model Equations for Long Waves in Nonlinear Dispersive Systems", Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences , 272 (1220): 47–78, Bibcode :1972RSPTA.272...47B , doi :10.1098/rsta.1972.0032 , JSTOR 74079 , S2CID 120673596 Dingemans, M.W. (1997), Wave propagation over uneven bottoms 13 , World Scientific, Singapore, ISBN 978-981-02-0427-3 the original on 2012-02-08, retrieved 2009-04-18 2부 6장을 참조 하십시오.Korteweg, D. J. ; de Vries, G. (1895), "On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves" , Philosophical Magazine , 39 (240): 422–443, doi :10.1080/14786449508620739 추가 정보 Benjamin, T.B. ; Lighthill, M.J. (1954), "On cnoidal waves and bores", Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences , 224 (1159): 448–460, Bibcode :1954RSPSA.224..448B , doi :10.1098/rspa.1954.0172 , S2CID 119869484 de Jager, E.M. (2006). "On the origin of the Korteweg–de Vries equation". arXiv :math/0602661v1 Drazin, P.G. ; Johnson, R.S. (1996), Solitons: an introduction , Cambridge University Press, ISBN 978-0-521-33655-0 Fenton, J.D. (1979), "A high-order cnoidal wave theory", Journal of Fluid Mechanics , 94 (1): 129–161, Bibcode :1979JFM....94..129F , doi :10.1017/S0022112079000975 Keulegan, G.H.; Patterson, G.W. (1940), "Mathematical theory of irrotational translation waves" , Journal of Research of the National Bureau of Standards , 24 (January): 47–101, doi :10.6028/jres.024.027 Miles, J.W. (1981), "The Korteweg–de Vries equation: a historical essay", Journal of Fluid Mechanics , 106 : 131–147, Bibcode :1981JFM...106..131M , doi :10.1017/S0022112081001559 Wehausen, J.V. ; Laitone, E.V. (1960), "Surface waves", in Flügge, S. ; Truesdell, C. (eds.), Encyclopedia of Physics the original on 2009-01-05, retrieved 2009-04-18 Wiegel, R.L. (1960), "A presentation of cnoidal wave theory for practical application", Journal of Fluid Mechanics , 7 (2): 273–286, Bibcode :1960JFM.....7..273W , doi :10.1017/S0022112060001481







































![{\begin{aligned}0&=\int _{0}^{{\lambda }}\eta (\xi )\;{\text{d}}\xi =2\,\int _{0}^{{{\tfrac 12}\lambda }}\left[\eta _{2}+\left(\eta _{1}-\eta _{2}\right)\,\operatorname {cn}^{2}\,\left({\begin{array}{c|c}\displaystyle {\frac {\xi }{\Delta }}&m\end{array}}\right)\right]\;{\text{d}}\xi \\&=2\,\int _{0}^{{{\tfrac 12}\pi }}{\Bigl [}\eta _{2}+\left(\eta _{1}-\eta _{2}\right)\,\cos ^{2}\,\psi {\Bigr ]}\,{\frac {{\text{d}}\xi }{{\text{d}}\psi }}\;{\text{d}}\psi =2\,\Delta \,\int _{0}^{{{\tfrac 12}\pi }}{\frac {\eta _{1}-\left(\eta _{1}-\eta _{2}\right)\,\sin ^{2}\,\psi }{{\sqrt {1-m\,\sin ^{2}\,\psi }}}}\;{\text{d}}\psi \\&=2\,\Delta \,\int _{0}^{{{\tfrac 12}\pi }}{\frac {\eta _{1}-m\,\left(\eta _{1}-\eta _{3}\right)\,\sin ^{2}\,\psi }{{\sqrt {1-m\,\sin ^{2}\,\psi }}}}\;{\text{d}}\psi =2\,\Delta \,\int _{0}^{{{\tfrac 12}\pi }}\left[{\frac {\eta _{3}}{{\sqrt {1-m\,\sin ^{2}\,\psi }}}}+\left(\eta _{1}-\eta _{3}\right)\,{\sqrt {1-m\,\sin ^{2}\,\psi }}\right]\;{\text{d}}\psi \\&=2\,\Delta \,{\Bigl [}\eta _{3}\,K(m)+\left(\eta _{1}-\eta _{3}\right)\,E(m){\Bigr ]}=2\,\Delta \,{\Bigl [}\eta _{3}\,K(m)+{\frac {H}{m}}\,E(m){\Bigr ]},\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9858bd7674e85b2bdcc18b966a189e6e565d085d)














 통해 인자 c를 제거하여 KdV 방정식과 BBM 방정식 모두에서 동일한 1차 상미분 방정식을 얻을 수 있다.단, 여기서는 앞의 방정식에 제시된 형식을 사용한다.그 결과, KdV 방정식에서 발견된 것과 같은 δ에 대한 공식은 다릅니다.
통해 인자 c를 제거하여 KdV 방정식과 BBM 방정식 모두에서 동일한 1차 상미분 방정식을 얻을 수 있다.단, 여기서는 앞의 방정식에 제시된 형식을 사용한다.그 결과, KdV 방정식에서 발견된 것과 같은 δ에 대한 공식은 다릅니다.

![{\begin{aligned}\eta (x,t)&=\eta _{2}+H\,\operatorname {cn}^{2}\left({\begin{array}{c|c}\displaystyle {\frac {x-c\,t}{\Delta }}&m\end{array}}\right),\\\eta _{2}&={\frac {H}{m}}\,\left(1-m-{\frac {E(m)}{K(m)}}\right),\\\Delta &=h\,{\sqrt {{\frac {4}{3}}\,{\frac {m\,h}{H}}\,{\frac {c}{{\sqrt {g\,h}}}}}}&&={\frac {\lambda }{2\,K(m)}},\\\lambda &=h\,{\sqrt {{\frac {16}{3}}\,{\frac {m\,h}{H}}\,{\frac {c}{{\sqrt {gh}}}}}}\;K(m),\\c&={\sqrt {gh}}\,\left[1+{\frac {H}{m\,h}}\,\left(1-{\frac 12}\,m-{\frac 32}\,{\frac {E(m)}{K(m)}}\right)\right]&&{\text{and}}\\\tau &={\frac {\lambda }{c}}.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca57381bfc686a1420f5942f568906cce47bb455)











![{\begin{aligned}K(m)&={\frac {\pi }{2}}\,\left[1+\left({\frac 12}\right)^{2}\,m+\left({\frac {1\,\cdot \,3}{2\,\cdot \,4}}\right)^{2}\,m^{2}+\left({\frac {1\,\cdot \,3\,\cdot \,5}{2\,\cdot \,4\,\cdot \,6}}\right)^{2}\,m^{3}+\cdots \right],\\E(m)&={\frac {\pi }{2}}\,\left[1-\left({\frac 12}\right)^{2}\,{\frac {m}{1}}-\left({\frac {1\,\cdot \,3}{2\,\cdot \,4}}\right)^{2}\,{\frac {m^{2}}{3}}-\left({\frac {1\,\cdot \,3\,\cdot \,5}{2\,\cdot \,4\,\cdot \,6}}\right)^{2}\,{\frac {m^{3}}{5}}-\cdots \right].\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a8fa88a458fd8929c14bef603f346c6841e4bb4)
















![c={\sqrt {gh}}\,\left[1+{\frac {H}{m\,h}}\,\left(1-{\frac 12}\,m-{\frac 32}\,{\frac {E(m)}{K(m)}}\right)\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/01cc17da57e1dbf3ab205df5bfdd091c82718797)



![c={\sqrt {gh}}\,\left[1+(\kappa \,h)^{2}\,{\frac {4}{3\,\pi ^{2}}}\,K^{2}(m)\,\left(1-{\frac 12}\,m-{\frac 32}\,{\frac {E(m)}{K(m)}}\right)\right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/e925078a7c33910437ef6855adbdddc3b6f88167)


![c={\Bigl [}1-{\tfrac 16}\,\left(\kappa h\right)^{2}{\Bigr ]}\,{\sqrt {g\,h}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/06539f6de1897886a721731db35dddeb949c15a8)



![{\begin{aligned}Q&=\int _{0}^{{\zeta (\xi )}}\partial _{z}\Psi \;{\text{d}}z,\\R&={\frac {p}{\rho }}+{\tfrac 12}\,{\Bigl [}\left(\partial _{\xi }\Psi \right)^{2}+\left(\partial _{z}\Psi \right)^{2}{\Bigr ]}+g\,z\qquad {\text{and}}\\S&=\int _{0}^{{\zeta (\xi )}}\left[{\frac {p}{\rho }}+\left(\partial _{z}\Psi \right)^{2}\right]\;{\text{d}}z.\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c724184e53307d8d1b54979ae1340007981bdaf2)




![h_{c}={\sqrt[ {3}]{{\frac {Q^{2}}{g}}}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc53aae236ba451c5cd2738826759e70a298043)




![S=R\,\zeta -{\tfrac 12}\,g\,\zeta ^{2}+\int _{0}^{\zeta }{\tfrac 12}\left[\left(\partial _{z}\Psi \right)^{2}-\left(\partial _{\xi }\Psi \right)^{2}\right]\;{\text{d}}z.](https://wikimedia.org/api/rest_v1/media/math/render/svg/514e0c8da01c709d5746c4edb53010efb06581c9)







![\partial _{t}\left({\tfrac 12}\,\eta ^{2}\right)+\partial _{x}\left\{{\tfrac 12}\,{\sqrt {g\,h}}\,\eta ^{2}+{\tfrac 12}\,{\sqrt {{\frac {g}{h}}}}\,\eta ^{3}+{\tfrac 1{12}}\,h^{2}{\sqrt {g\,h}}\,\left[\partial _{x}^{2}\left(\eta ^{2}\right)-3\left(\partial _{x}\eta \right)^{2}\right]\right\}=0,](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72e37ab27cff2f96b425d37e79bcc93dcb46d83)
![{\begin{aligned}{\frac {1}{\lambda }}\,\int _{0}^{\lambda }\eta ^{2}\;{\text{d}}x&={\frac {1}{\lambda }}\int _{0}^{\lambda }\left\{\eta _{2}+H\,\operatorname {cn}^{2}\left({\begin{array}{c|c}\displaystyle {\frac {\xi }{\Delta }}&m\end{array}}\right)\right\}^{2}\;{\text{d}}\xi ={\frac {H^{2}}{\lambda }}\int _{0}^{\lambda }\operatorname {cn}^{4}\left({\begin{array}{c|c}\displaystyle {\frac {\xi }{\Delta }}&m\end{array}}\right)\;{\text{d}}\xi -\eta _{2}^{2}\\&={\frac {\Delta \,H^{2}}{\lambda }}\int _{0}^{{\pi }}\cos ^{4}\,\psi \,{\frac {{\text{d}}\xi }{{\text{d}}\psi }}\;{\text{d}}\psi -\eta _{2}^{2}={\frac {H^{2}}{2\,K(m)}}\int _{0}^{{\pi }}{\frac {\cos ^{4}\,\psi }{{\sqrt {1-m\,\sin ^{2}\,\psi }}}}\;{\text{d}}\psi -\eta _{2}^{2}\\&={\frac 13}\,{\frac {H^{2}}{m^{2}}}\,\left[\left(2-5\,m+3\,m^{2}\right)+\left(4\,m-2\right)\,{\frac {E(m)}{K(m)}}\right]-{\frac {H^{2}}{m^{2}}}\,\left(1-m-{\frac {E(m)}{K(m)}}\right)^{2}\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/241df305c1a0cdad90d96bedcd2def8a495d3dfd)
![E_{{\text{pot}}}={\tfrac 12}\,\rho \,g\,H^{2}\,\left[-{\frac {1}{3\,m}}+{\frac {2}{3\,m}}\,\left(1+{\frac {1}{m}}\right)\left(1-{\frac {E(m)}{K(m)}}\right)-{\frac {1}{m^{2}}}\,\left(1-{\frac {E(m)}{K(m)}}\right)^{2}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a9820b3d9fa4dbe108096668b8c714ba4575219)