평활-입자 수역학

평활-입자 수역학(SPH)은 고체 역학과 유체 흐름과 같은 연속체 매체의 역학을 시뮬레이션하는 데 사용되는 연산 방법이다. 그것은 Gingold와 Monahan^[2] 그리고 Lucy에^[3] 의해 1977년에 개발되었는데, 처음에는 천체물리학적 문제들을 위해 개발되었다. 그것은 천체물리학, 탄도학, 화산학, 해양학 등 많은 연구 분야에서 사용되어 왔다. 메쉬프리스 라그랑지안법(유체와 함께 좌표가 이동하는 곳)으로 밀도 등 변수에 대해 쉽게 방법의 분해능을 조절할 수 있다.

방법

이점

• 시공에 의한 SPH는 메쉬프리 방식으로, 자유 표면 흐름이나 큰 경계 변위 등 복잡한 경계 역학이 지배하는 문제를 시뮬레이션하는 데 이상적으로 적합하다.
• 메쉬의 부족은 다핵심 아키텍처의 경우에도 모델 구현과 병렬화를 상당히 단순화시킨다.^[4][5]

• SPH는 모델링 물리학에서 논의한 바와 같이 다양한 분야로 쉽게 확장될 수 있으며, 일부 다른 모델과 혼합될 수 있다.
• 약하게 압축할 수 있는 SPH에 관한 섹션에서 논의된 바와 같이, 이 방법은 큰 보존 특성을 가지고 있다.
• 관심 측정 지표가 유체 밀도와 관련된 경우(예: 밀도 변동의 확률밀도함수) 입자 수 당 SPH 시뮬레이션의 계산 비용은 셀 수 당 그리드 기반 시뮬레이션 비용보다 유의하게 적다.^[6] SPH에서는 문제가 있는 곳에 해결책이 놓이기 때문이다.

제한 사항

• 인렛, 콘센트, 벽면 등 SPH에서 경계 조건을 설정하는 것은 그리드 기반 방법보다 더 어렵다. 사실, "경계 조건의 처리는 확실히 SPH 방법의 가장 어려운 기술적 포인트 중 하나"라고 명시되어 있다.^[9] 이 도전은 부분적으로 SPH에서 경계 근처의 입자가 시간에 따라 변하기 때문이다.^[10] 그럼에도 불구하고 SPH에 대한 벽 경계 조건을 사용할 수 있다.
• 관심 메트릭이 밀도와 관련이 없는 경우(예: 운동 에너지 스펙트럼) 입자 수 당 SPH 시뮬레이션 계산 비용은 셀 수 당 그리드 기반 시뮬레이션 비용보다 상당히 크다.^[6] 따라서 병렬 속도 상승의 문제를 간과한 채 일정한 밀도 흐름(예: 외부 공기역학)의 시뮬레이션은 SPH보다 그리드 기반 방법으로 더 효율적이다.

예

유체 역학

부드러운 입자 수역학도 유체 운동을 모형화하는 데 점점 더 많이 사용되고 있다. 이것은 전통적인 그리드 기반 기술에 비해 몇 가지 이득 때문이다. 첫째, SPH는 입자 자체가 질량을 나타내기 때문에 별도의 계산 없이 질량의 보존을 보장한다. 둘째로, SPH는 방정식의 선형 시스템을 푸는 것보다 인접 입자의 가중 기여에 의한 압력을 계산한다. 마지막으로, 유체 경계를 추적해야 하는 그리드 기반 기법과는 달리, SPH는 입자가 밀도 높은 유체(보통 물)를 나타내고 빈 공간은 가벼운 유체(보통 공기)를 나타내기 때문에 직접 2상 상호작용 유체를 위한 자유 표면을 생성한다. 이러한 이유로 SPH를 이용한 유체 운동을 실시간으로 시뮬레이션할 수 있다. 그러나 그리드 기반 기법과 SPH 기법 모두 메타볼과 행군 큐브, 포인트 스플래팅 또는 '카펫' 시각화와 같은 폴리곤화 기법을 사용한 렌더링 가능한 자유 표면 기하학의 생성이 여전히 필요하다. 가스 역학의 경우 가스 칼럼 밀도의 렌더링을 생성하기 위해 커널 함수 자체를 사용하는 것이 더 적합하다(예: SPLASH 시각화 패키지에서 수행된 것과 동일).

그리드 기반 기술에 대한 한 가지 단점은 등가 분해능의 시뮬레이션을 생성하기 위해 다수의 입자가 필요하다는 것이다. 균일한 그리드와 SPH 입자 기법의 일반적인 구현에서는 렌더링되지 않는 물의 양을 채우기 위해 많은 복셀 또는 입자가 사용될 것이다. 그러나 이러한 시스템에서 불압력 조건을 강제하기 쉽기 때문에 특히 입자 방법(입자 수준 세트 등)과 결합된 정교한 그리드 기반 기법으로 정확도가 상당히 높아질 수 있다. 유체 시뮬레이션을 위한 SPH는 상호 작용성만큼 정확성이 중요하지 않은 실시간 애니메이션과 게임에서 점점 더 많이 사용되고 있다.

유체 시뮬레이션을 위한 SPH의 최근 연구는 성능, 정확성 및 적용 영역을 증가시켰다.

• B. Solentaler, 2009년 PCISPH(예측-정확성 SPH)를 개발하여 더 나은 비압축성 제약조건을^[12] 허용한다.
• M. Ihmsen 외, 2010년, 정확한 강성 신체 상호작용을^[13] 위해 PCISPH에 대한 경계 취급 및 적응형 타임 스텝 도입
• K. Bodin 외, 2011, 상태 압력의 표준 방정식을 밀도 제약으로 대체하고 가변 시간 통합자를^[14] 적용한다.
• R. Hoetzlein, 2012, Fluid v.3에서^[15] 대형 장면을 위한 효율적인 GPU 기반 SPH 개발
• N. Akinci 등, 2012년, 유체역동력을 완전히 기반으로 한 다목적 경계 취급 및 양방향 SPH-강화 커플링 기법을 도입한다. 접근방식은 다양한 유형의 SPH 솔버에 적용할 수 있다.
• M. Macklin 등, 2013년, Position Based Dynamics 프레임워크 내부의 압축 불가능한 흐름을 시뮬레이션하여 더 큰 시간 스텝을 확보함
• N. Akinci 외, 2013년에는 현실에서 관찰되는^[18] 다양한 흥미로운 물리적 효과를 시뮬레이션할 수 있는 다목적 표면 장력과 양방향 유체 고체 접착 기술을 도입한다.
• J. 카일과 E. 2013년 Terrell, SPH를 풀필름 윤활에^[19] 도포
• A. 마하비와 N. 2015년 Talbbbedokhti는 견고한 경계 조건의 구현을 위한 하이브리드 알고리즘을 제안하고 날카로운 파고들어진 보 위의^[20] 흐름을 시뮬레이션한다.
• S. Tavakkol 등, 2016년, 입자의 수평 및 수직 크기를 독립시키고 곡선 경계를^[21] 따라 균일한 질량 분포를 생성하는 곡선SPH를 개발한다.
• W. 코스토르츠와 A. Esmail-Yakas, 2020년, 부분-평면 경계^[11] 근처의 정규화 요인을 평가하기 위한 일반적이고 효율적이며 간단한 방법을 제안한다.
• Collagrosi 등, 2019년, 자유 표면에 가까운 실린더 주위의 흐름 연구 및 다른 기법과의 비교

천체물리학

평활-입자 수역학의 적응 분해능, 물리적으로 보존된 양의 수치적 보존, 그리고 많은 수의 크기를 포함하는 현상을 시뮬레이션하는 능력은 이론 천체물리학에서 연산에 이상적이다.^[22]

은하 형성, 항성 형성, 별 충돌,^[23] 초신성^[24] 및 유성 충돌의 시뮬레이션은 이 방법의 광범위한 천체물리학 및 우주론적 사용의 일부다.

SPH는 가능한 중력의 영향을 포함하여 유체역학적 흐름을 모델링하는 데 사용된다. 복사 전달과 자기장과 같이 중요할 수 있는 다른 천체물리학적 과정들을 통합하는 것은 천문학계에서 활발한 연구 영역이며, 약간의 제한적인 성공을 거두었다.^[25][26]

고체 역학

리베르스키와 펫체크는^[27][28] SPH를 솔리드 메카닉스로 확장했다. 이 애플리케이션에서 SPH의 주요 장점은 그리드 기반 방법보다 더 큰 국소 왜곡을 처리할 수 있다는 것이다. 이 기능은 Solid Mechanics의 많은 응용분야에서 활용되었다: 금속성형, 충격, 균열성장, 균열, 파편화 등.

일반적으로 메쉬프리스 방법, 특히 SPH의 또 다른 중요한 장점은 메쉬프리스의 특성을 고려할 때 메쉬피존성 문제가 자연적으로 회피된다는 것이다. 특히 메쉬 정렬은 균열과 관련된 문제와 관련이 있으며, 커널 함수의 등방성 지지 때문에 SPH에서는 피한다. 그러나 고전적인 SPH 제형은 인장 불안정성과^[29] 일관성의 결여로 인해 어려움을 겪는다.^[30] 지난 수년간 SPH 솔루션의 정확도를 높이기 위해 서로 다른 보정이 도입되어 류 외 연구원이 RKPM을 이끌어냈다.^[31] 랜들스와 리버스키^[32], 존슨과 비셀은^[33] 충격 현상에 대한 연구에서 일관성 문제를 해결하려고 노력했다.

다이카 외 연구진, 랜들스 및 리베르스키는^[36] SPH에 응력점 통합을 도입했고 테드 벨리츠코 외 연구진은 응력점 기법이 가상의 단수 모드로 인한 불안정성을 제거하는 반면 인장 불안정성은 라그랑지안 커널을 사용함으로써 피할 수 있다는 것을 보여주었다.^[34][35][37] SPH 방법의 융합을 개선하기 위해 헌신한 문헌에서 다른 많은 최근의 연구들을 발견할 수 있다.

최근 SPH의 수렴과 안정성을 이해하는 개선으로 인해 솔리드 메카니즘에서 보다 광범위한 응용이 가능해졌다. 그 밖의 적용 사례와 방법의 개발 예는 다음과 같다.

• 금속 형성 시뮬레이션.^[38]
• William G에 의한 고형물의 충격 파괴에 대한 SPH 기반 방법 SPM(Smoothed Particle Applied Mechanics) 후버.^[39]
• 골절 및 단편화에 대한 수정된 SPH(SPH/MLSPH)^[40]
• 고형물 내 충격파 전파용 TSPH(Taylor-SPH)^[41]
• 일반화 좌표 SPH(Generalized coordination SPH, GSPH)는 입자를 데카르트 좌표계에 불균등하게 할당하고 입자가 균일한 간격으로 정렬되는 일반화 좌표계에서의 매핑을 통해 배치한다.^[42]

숫자 도구

보간

평활-입자 수역학(SPH) 방법은 유체를 입자라 불리는 이산 이동 $요소{\displaystyle }$ i${\displaystyle ,}$ ${\displaystyle j}$, ${\displaystyle$ i$,j$ 세트로 나누어 작용한다. 이들의 라그랑지안적 특성은 속도 $v{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$$${$r} _{i}$을(를) 통합하여$$ 다음과 같이$$ $위치$를 설정할 수 있다.

${\displaystyle {\frac {d} {\mathsymbol {r}_{i}}{\mathmbol {d} t}={\mathmbol {v}_{i}}.}$

이러한 입자들은 일반적으로 $h{\displaystyle }$ ${\displaystyle h}$로 표현되는 "스무팅 길이"로 알려진 특성 반경과 커널 함수를 통해 상호작용한다$.$ 이는 어떤 입자의 물리적 양도 커널의 범위 내에 있는 모든 입자의 관련 특성을 합산하여 얻을 수 있다는 것을 의미한다.가중치 함수 $W{\displaystyle }$ ${\displaystyle W}$로 사용됨$.$ 이것은 두 단계로 이해할 수 있다. 첫 번째 임의 $필드{\displaystyle }$ A$${\$displaystyle$A}은(는) W$${\$displaystyle W}$을(를) 사용한 콘볼루션으로 작성된다$.$

${\displaystyle A({\boldsymbol{r}}=\int A\왼쪽({\boldsymbol {r^{\premium }}\오른쪽)W({\boldsymbol{r}-{\boldsymbol {r^{\prime },h)\,\mathrm {d}V\!\왼쪽({\boldsymbol {r^{\prime }}\오른쪽).}$

위의 근사치를 만드는 오류는 순서 $h{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ 둘째, 적분은 입자에 대한 리만 합계를 사용하여 근사치를 구한다.

${\displaystyle A({\boldsymbol{r}})=\sum _{j}V_{j}A_{j}W({\boldsymbol {r}-{\boldsymbol {r}_{j},h),}$

$여기$서 j ${\displaystyle j}$에 대한 합계는 시뮬레이션의 모든 입자를 포함한다$$. ${\displaystyle V_{}}$ ${\displaystyle j_{}}$ ${\$는 입자 $j{\displaystyle }$ ${\displaystyle j}$의 볼륨이고$,$ $A{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$는 입자 $j{\displaystyle }$ ${\displaystyle j}$에 대한 $수량{\displaystyle }$ A ${\displaystystyle A}$의 값이며$,$ r ${\displaystymbol{r$}은 위치를 나타낸다$$. 예를 들어 ${\displaystyle {입자}_{}}$ $i{\displaystyle }$ ${\displaystyle$ $\rho_{i$$}$의 밀도는 다음과 같이 표현할 수 있다$$.

${\displaystyle \rho _{i}=\rho({\displaysymbol {r}_{i}}=\sum _{j}m_{j}}W_{ij}}$

여기서 $m{\displaystyle {}_{}}$ ${\displaystyle j_{}}$= ${\displaystyle {\rho j}_{}}$ v ${\displaystyle j_{}}$ ${\$는 입자 질량과 ${\displaystyle {\rho }_{}}$ j ${\$ 입자$$ 밀도를 나타내고$$ ${\displaystyle {Wi}_{}}$ ${\displaystyle j_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$ i ${\$$W_{ji}}$ is a short notation for ${\displaystyle W( {\boldsymbol {r}}_{i}-{\boldsymbol {r}}_{j} ,h)}$. The error done in approximating the integral by a discrete sum depends on ${\displaystyle h}$, on the particle size (i.e. ${\displaystyle V_{j}^{1/d}}$, ${\displ$$aystyle d}$이(가$$) 공간 차원) 및 공간 내 입자 배열. 후자의 효과는 아직 잘 알려져 있지 않다.^[43]

일반적으로 사용되는 커널 함수는 가우스 함수, 5중 스플라인, 웬들랜드 ${\displaystyle {C\mathrm{}}^{}}$ 2 ${\$ C$^{2$}}$$커널을$$ 포함한다.^[44] 후자의 두 개의 낟알은 $h{\displaystyle }$ ${\displaystyle h$}에 비례하는 지원으로 (제한된 거리에 작은 기여가 있는 가우스와는 달리) 콤팩트하게 지원된다$.$ 이는 먼 입자의 비교적 작은 기여를 포함하지 않음으로써 계산 노력을 절약할 수 있는 장점이 있다.

스무딩 길이의 크기는 공간과 시간 모두에서 고정할 수 있지만, 이는 SPH의 전체 파워를 이용하지 않는다. 각 입자에 자체적인 스무딩 길이를 할당하고 시간에 따라 달라질 수 있도록 함으로써 시뮬레이션의 분해능을 만들어 국소 조건에 따라 자동으로 적응할 수 있다. 예를 들어 많은 입자가 서로 가까이 있는 매우 밀집된 지역에서 평활 길이는 상대적으로 짧게 만들어 높은 공간 분해능을 산출할 수 있다. 반대로 개별 입자가 멀리 떨어져 있고 분해능이 낮은 저밀도 영역에서는 스무딩 길이를 늘려 관심 영역에 대한 연산을 최적화할 수 있다.

지배 방정식의 해석

일정한 질량의 입자의 경우 시간 수율에 따라$$ 보간 밀도 $\rho {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$를 구별한다.

${\dplaystyle {\frac {d\rho_{dt}=\sum _{j}}\{j}\좌측({\boldsymbol{v}}-{\boldsymbol{v}-{v}_{j}\오른쪽)\cdot \nabla W_{ij}}}}}}}$

where ${\displaystyle \nabla W_{ij}=-\nabla W_{ji}}$ is the gradient of ${\displaystyle W_{ij}}$ with respect to ${\displaystyle {\boldsymbol {r}}_{i}}$. Comparing this equation with the continuity equation in the Lagrangian description (using material derivatives),

${\displaystyle {\frac {d\rho }{dt}=-\rho \cdla \cdot {\cdsymbol{v},}$

오른쪽이 -${\displaystyle \rho }$ ${\displaystyle \mathrm{\nabla }}$ $⋅$ ${\displaystyle v\mathbf{}}${\$displaystyle$-\$rho \cdla \cdot \mathbf$ {$v$의 근사치임을 알 수 있으므로, 다음과 같이 이산 발산 연산자를 정의한다.

${\displaystyle \operatorname {D} _{i}\left\{{\boldsymbol {v}}_{j}\right\}=-{\frac {1}{\rho _{i}}}\sum _{j}m_{j}\left({\boldsymbol {v}}_{i}-{\boldsymbol {v}}_{j}\right)\cdot \nabla W_{ij}.}$

This operator gives an SPH approximation of ${\displaystyle \nabla \cdot \mathbf {v} }$ at the particle ${\displaystyle i}$ for a given set of particles with given masses ${\displaystyle m_{j}}$, positions ${\displaystyle \left\{\mathbf {r} _{j}\right\}}$ and velocities ${\displaystyle \left\{{\mathbf{v}}_j\right\}}$${\displaystyle \left\{\mathbf {v} _{j}\$오른쪽$\backslash \}\}\}.$

압축 불시 유체의 다른 중요한 방정식은 운동량 균형에 대한 오일러 방정식이다.

${\dfrac{\frac{\frmbol{v}}{dt}=-{\frac {1}{\rho}}\p+{\fla symbol{g}}}}$

연속성과 마찬가지로, 과제는 쓰기 위해 이산 그라데이션 연산자를 정의하는 것이다.

${\d}디스플레이스타일 {\frac{\boldsymbol{v}_{dt}=-{\frac{1}{1}{\rho}}}\operatorname {\mathbf {G} _{i}\왼쪽\{p_{j}\rig\}+{\boldsymbol}}}}}}}}}}$

한 가지 선택은

${\displaystyle \operatorname {\mathbf {G} } _{i}\left\{p_{j}\right\}=\rho _{i}\sum _{j}m_{j}\left({\frac {p_{i}}{\rho _{i}^{2}}}+{\frac {p_{j}}{\rho _{j}^{2}}}\right)\nabla W_{ij},}$

그것은 위의 발산 연산자와 꼬치꼬치 붙는 성질을 가지고 있다.

${\displaystyle \sum _{i}V_{i}{\boldsymbol {v}}_{i}\cdot \operatorname {\mathbf {G} } _{i}\left\{p_{j}\right\}=-\sum _{i}V_{i}p_{i}\operatorname {D} _{i}\left\{{\boldsymbol {v}}_{j}\right\},}$

이것은 연속체 정체성의 이산형 버전이다.

${\displaystyle \int{\b}\cdot \cdotname {grad} p=-\int p\p\divname {div} \cdot {\\cdmbol {v}.}$

이 재산은 훌륭한 보존 재산으로 이어진다.^[45]

또한 이러한 선택은 대칭 발산 연산자와 대칭 구배를 초래한다는 점에 유의하십시오. 오일러 방정식에서 압력 구배를 탈피하는 방법에는 여러 가지가 있지만 위의 대칭성이 가장 인정된다. 선형 및 각운동량의 엄격한 보존을 지원한다. 즉, 입자 $j{\displaystyle }$ ${\displaystyle j}$에 의해 $입자{\displaystyle }$ i ${\displaystyle$ j$}$에 가해지는 힘은 대칭 속성 $\nabla {\displaystyle \mathrm{}}$ W ${\displaystyle i_{}}$= -${\displaystyle \mathrm{\nabla }}$ W j ${\displaystyle {덕분}_{}}$에 유효 방향의 기호 변경을 포함하여$$ 입자 $i{\displaystyle }$ ${\displaystyle i}$에 의해 입자 j ${\displaystystyle j}$에 가해지는 힘과 같다는$$ 뜻이다.${\displaystyle i_{}}$ ${\$

그럼에도 불구하고, 수적으로나 물리적으로 더 나은 성능을 발휘할 수 있는 다른 운영자들이 제안되었다. 예를 들어, 이러한 연산자의 한 가지 단점은 $다이버전스{\displaystyle \mathrm{}}$ D$${\$displaystyle \operatorname {D}이($가) 0순서가 일치하지만$$(즉, 상수 벡터 필드에 적용하면 0이 된다) 그라데이션 $G{\displaystyle \mathbf{}}$ ${\$이(가)이(가 아니라는$$ 것을 알 수 있다. 이 문제를 회피하기 위해 몇 가지 기법이 제안되었고, 이는 새로운 운영자로 이어졌다(예: 참조).^[46]

변동 원리

위의 SPH 지배 방정식은 입자 시스템의 라그랑지안으로부터 시작하여 최소 작용 원리에서 도출할 수 있다.

${\displaystyle {\mathcal {L}}=\sum _{j}m_{j}\left({\tfrac {1}{2}}{\boldsymbol {v}}_{j}^{2}-e_{j}+{\boldsymbol {g}}\cdot {\boldsymbol {r}}_{j}\right)}$,

여기서 $e{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$는 입자별 내부 에너지다. Euler-Lagrange 방정식은 각 입자에 대해 다음과 같이 읽는다.

${\displaystyle {\frac {\mathrm {d}{{d}}{{\frac {\partial {\mathcal {v}{i}}}}}}{\partial {\boldsymbol {\mathcal}{L}}}}}}}}}}}{partial {\bmathmathmaxmaximbol {d}}}}}}}}}}.}$

위의 라그랑지안에 적용하면 다음과 같은 운동 방정식을 제공한다.

${\displaystyle m_{i}{\frac {\mathrm {d} {\boldsymbol {v}}_{i}}{\mathrm {d} t}}=-\sum _{j}m_{j}{\frac {\partial e_{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i}{\boldsymbol {g}}=-\sum _{j}m_{j}{\frac {\partial e_{j}}{\partial \rho _{j}}}{\frac {\partial \rho _{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i}{\boldsymbol {g}}}$

체인 규칙이 사용된 경우, e ${\displaystyle j_{}}$ ${\$은$($는) $\$ j {\$displaystyle \rho_{j}$에 의존하고$$, 후자는 입자의 위치에 의존하기 때문이다. 열역학 속성 ${\displaystyle d}$ e${\displaystyle }$=${\displaystyle }$( ${\displaystyle p}$/ ${\displaystyle {\rho \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) d ${\displaystyle d\mathrm{}}$ ${\displaystyle d}$ d d$$\$displaystyle \mathrm {d} e=\left(p/\rho ^{2}\right)\mathrm {d} \rho }$을(를) 사용하면 쓸 수 있다.

${\displaystyle m_{i}{\frac {\mathrm {d} {\boldsymbol {v}}_{i}}{\mathrm {d} t}}=-\sum _{j}m_{j}{\frac {p_{j}}{\rho _{j}^{2}}}{\frac {\partial \rho _{j}}{\partial {\boldsymbol {r}}_{i}}}+m_{i}{\boldsymbol {g}},}$

SPH 밀도 보간술의 ${\displaystyle \frac{{}_{}}{}}$를 꽂고 명시적으로 ${\displaystyle \frac{{differentiating}_{}}{}}{\displaystyle \frac{\mathrm{}}{}}$j ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\${\$boldsymbol{r}_{i}}}}}}}$을(를) 구별하면 다음과 같은 결과를$$ 얻을 수 있다.

${\displaystyle {\frac {\mathrm {d} {\boldsymbol {v}}_{i}}{\mathrm {d} t}}=-\sum _{j}m_{j}\left({\frac {p_{i}}{\rho _{i}^{2}}}+{\frac {p_{j}}{\rho _{j}^{2}}}\right)\nabla W_{ij}+{\boldsymbol {g}},}$

즉, SPH 모멘텀 방정식이 이미 언급되어 있으며, $여기$서 G ${\$연산자를$$ 인식한다. 이는 선형 운동량이 보존되는 이유를 설명하고 각 운동량과 에너지를 보존할 수 있게 한다.^[47]

시간 통합

대형 액셀러레이터에서 점성 입자의 수치적 통합에 관한 80년대와 90년대에 행해진 작업으로부터, 적절한 시간 통합자들은 장기적으로 정확한 보존 특성을 가지고 개발되었다; 그것들은 동정적 통합자라고 불린다. SPH 문헌에서 가장 인기 있는 것은 각 $입자{\displaystyle }$ i ${\displaystyle i}$에 대해 읽는 비약적 구조다$.$

${\displaystyle{\begin{정렬}{\boldsymbol{v}}_{나는}^{n+1/2}&, ={\boldsymbol{v}}_{나는}^{n}+{\boldsymbol{}}_{나는}^{n}{\frac{\Delta지}{2}},\\{\boldsymbol{r}}_{나는}^{n+1}&, ={\boldsymbol{r}}_{나는}^{n}+{\boldsymbol{v}}_{나는}^{i+1/2}\Delta t,\\{\boldsymbol{v}}_{나는}^{n+1}&, ={\boldsymbol{v}}_{나는}^{n+1/2}+{\boldsymbol{}}_{나는}^{i+1}{\frac{\Delta지}{2}.},\end{aligned}}$

여기서 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle t}$ ${\displaystyle \Delta t}$은 시간 단계, 위첨자는 시간 반복을 나타내며, ${\displaystyle {}_{}}$ ${\${\$boldsymbol{a}_{i}}}$는 운동 방정식의 우측에 의해 주어지는 입자 가속이다$$.

다른 공감 통합자가 존재한다(참고 교재 참조). 여러 번 반복한 후 오류가 누적되지 않도록 고순도 비순차 방식 대신 공감(순차마저 낮음) 방식을 사용하는 것이 좋다.

밀도 통합은 광범위하게 연구되지 않았다(자세한 내용은 아래 참조).

공감각적 계획은 보수적이지만 명시적이기 때문에 수치적 안정성은 Courant-Friedrichs-Lewy 조건과 유사하게 안정성 조건을 요구한다(아래 참조).

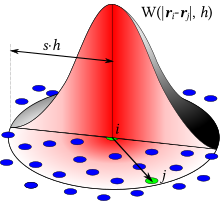
경계 기법

SPH 콘볼루션을 경계 가까이, 즉 s · h보다 더 가까운 곳에서 연습해야 하는 경우, 일체형 지지대가 잘린다. 실제로, 경계에 의해 경합이 영향을 받는 경우, 경합은 두 개의 통합으로 분할되어야 한다.

${\displaystyle A({\boldsymbol{r})=\int_{\Oomega({\boldsymbol{r}})}A\왼쪽({\boldsymbol {r^{\premy }}\오른쪽)W({\boldsymbol{r}-{\boldsymbol {r^{\premy}},h)d{\boldsymbol {r^{\premy}+\int_{B({\boldsymbol{r}})-\Oomega({\boldsymbolmbolmbol{r})}}}}}}}})A\왼쪽({\boldsymbol {r^{\premy }}\오른쪽)W({\boldsymbol{r}-{\boldsymbol {r^{\premy}},h)d{\boldsymbol {r^{\premy}},}$

여기서 B(r)는 r을 중심으로 한 콤팩트 서포트 볼이며, 반경 s · h를 가지고 있으며, Ω(r)은 계산 영역 내부의 컴팩트 서포트 부분인 Ω ∩ B(r)를 나타낸다. 따라서 SPH에서 경계 조건을 부과하는 것은 오른쪽 측면의 두 번째 적분 근사치에 완전히 기초한다. 미분 연산자 연산에도 물론 같은 것을 적용할 수 있다.

${\displaystyle \nabla A({\boldsymbol{r}})=\int_{\Oomega({\boldsymbol{r}})}A\left({\boldsymbol {r^{\prime }}}\right)\nabla W({\boldsymbol {r}}-{\boldsymbol {r^{\prime }}},h)d{\boldsymbol {r^{\prime }}}+\int _{B({\boldsymbol {r}})-\Omega ({\boldsymbol {r}})}A\왼쪽({\boldsymbol {r^{\premy }}\오른쪽)\나블라 W({\boldsymbol {r}-{\boldsymbol {r^{}},h)d{\boldsymbol {r^{\preme}}.}$

과거에 SPH에서 경계를 모형화하기 위해 몇 가지 기법이 도입되었다.

일체적 방심

가장 직접적인 경계 모델은 적분을 무시하는 것이고,

${\displaystyle \int_{B({\boldsymbol{r})-\Oomega({\boldsymbol{r}})}A\왼쪽({\boldsymbol {r^{\premy }}\오른쪽)\나블라 W({\boldsymbol {r^{\premy }h)d{\boldsymbol{r^{\premyme{}}}\simeq {\boldsymbol {0},}$

대량 상호작용이 고려될 수 있도록,

${\displaystyle \nabla A_{i}=\sum _{j\in \Oomega_{i}V_{j}A_{j}\나블라 W_{ij}.}$

이것은 단일 물질 시뮬레이션에서 자유 표면이 고려될 때 널리 사용되는 접근법이다.^[49]

이 경계 조건의 주된 이점은 명백한 단순성이다. 그러나 이 경계 기법을 적용할 때는 몇 가지 일관성 문제를 고려해야 한다.^[49] 그것은 사실 그것의 잠재적인 적용에 대한 큰 제한이다.

유체 익스텐션

아마도 SPH에서 경계 조건을 부과하는 가장 인기 있는 방법론, 또는 적어도 가장 전통적인 방법론은 유체 확장 기법일 것이다. 이러한 기법은 경계를 가로지르는 콤팩트한 지지대를 이른바 유령 입자로 채워서 자기장 값을 편리하게 부과하는 것을 기본으로 한다.^[50]

이 선을 따라, 일체형 방심 방법론은 A 필드가 계산 영역 밖으로 사라지는 유체 확장의 특정 사례로 간주할 수 있다.

이 방법론의 주요 이점은 경계 기여도가 대량 상호작용의 일부로 계산되는 경우 단순성이다. 또한 이 방법론은 문헌에서 깊이 분석되어 왔다.^[51][50][52]

반면에 잘린 영역에 유령 입자를 배치하는 것은 복잡한 경계 모양을 모델링하는 것이 번거로워질 정도로 사소한 작업이 아니다. 빈 영역을 유령 입자로 채우기 위해 가장 인기 있는 두 가지 접근법은 미러-파티클과 고정파티클이다.^[50]

경계 적분

가장 최근의 경계 기법은 경계 적분 방법론이다.^[54] 이 방법론에서 빈 볼륨 적분은 표면 적분으로 대체되며, 리노말화:

${\displaystyle \nabla A_{i}={\frac {1}{\gamma_{i}}\좌(\sum _{j\in \Oomega_{i}V_{j})A_{j}\nabla W_{ij}+\sum _{j\in \partial \Oomega_{i}}}S_{j}A_{j}{\boldsymbol{n}_{j}W_{ij}\오른쪽),}$

${\displaystyle \gamma _{i}=\sum _{j\in \Oomega_{i}V_{j}W_{ij}}$

일반_j j-th 경계 요소의 정규 분포를 n개 포함. 표면 항도 반분석적 표현을 고려해 풀 수 있다.^[54]

모델링 물리학

수력역학

약하게 압축 가능한 접근 방식

밀도를 결정하는 또 다른 방법은 SPH 스무딩 연산자 자체에 기초한다. 따라서 SPH 보간법을 활용한 입자분포에서 밀도를 추정한다. 커널 절단을 통해 자유 표면에서 원치 않는 오류를 극복하기 위해 밀도 제형이 다시 시간 내에 통합될 수 있다. ^[54]

유체 역학에서 약하게 압축할 수 있는 SPH는 Navier의 탈색에 기초한다.–압축성 유체에 대한 스톡스 방정식 또는 오일러 방정식 시스템을 닫기 위해 $적절한{\displaystyle }$ 상태의 방정식을 활용하여 압력 p ${\displaystyle p}$과 밀도 $\rho {\displaystyle }$ ${\displaystyle \rho }$을 연결한다$.$ 일반적으로 SPH에서는 소위 콜 방정식(때로는 "Tait 방정식"으로 잘못 언급되기도 한다)을 사용한다. 라고 쓰여 있다.

${\displaystyle p={\frac {\rho_{0}c^{2}}:{\lock}\frac {\rho _{0}\rho _{0}\right)^{\no }}{\1\p_{0}}}}}}}}}$

여기서 ${\displaystyle {\rho \mathrm{}}_{}}$ 0${\$$displaystyle \rho_{0}$는 기준$$$$ 밀도이며 c {\$displaystyle$ c$}$ 음속이다. 물의 경우 ${\displaystyle \mathrm{\gamma }}$= 7 ${\displaystyle \gamma =7}$이(가) 일반적으로 사용된다$$. 배경 압력 $p{\displaystyle {}_{}}$ ${\$을 추가하여 음의 압력 값을 피한다.

물과 같은 거의 압축할 수 없는 실제 유체는 10 $[\디스플레이$ 스타일 $10^{3}m/s}$의 음속의 매우 빠른 속도로 특징지어진다$.$ 따라서 압력 정보는 실제 대량 흐름과 비교하여 빠르게 이동하며, 이는 매우 작은 마하 수 $[\디스플레이$ 스타일$$M}]으로 이어진다$.$ 모멘텀 방정식은 다음과 같은 리로 이어진다.lation:

${\displaystyle {\fraca \delta \rho _{0}}\proxy {\frac {\\boldsymbol{v}}}}}{c^{2}}=M^{2}}:$

여기서 $\rho {\displaystyle }$ ${\displaystyle \rho}$은(는) 밀도 변화이고 $v{\displaystyle }$ ${\displaystyle$ v$}$은(는) 속도$$ 벡터다. 실제로 시간 통합 계획에서 시간 단계가 너무 작은 것을 피하기 위해 실제 값보다 작은 c 값을 채택한다. 일반적으로 1% 미만의 밀도 변화가 허용되도록 음속의 수치적 속도를 채택한다. 이른바 약압 가정이다. 이는 0.1보다 작은 마하 숫자에 해당하며, 이는 다음을 의미한다.

${\displaystyle c=10v_{\text{max}}}$

최대 $속도{\displaystyle {}_{}}$ ${\displaystyle {\text{vmax}}_{}}$ {\$displaystyle v_{\text{max}}$을(를) Torricelli의 법칙이나 숙련된 추측으로 추정해야 하는$$ 경우$.$ 작은 밀도 변화만 발생하므로 다음과 같은 상태의 선형 방정식을 채택할 수 있다.^[56]

${\displaystyle p=c^{2}\왼쪽(\rho -\rho _{0}\오른쪽)}$

일반적으로 약하게 압축할 수 있는 계획은 압력 및 밀도 장에 고주파 스퓨얼 소음에 의해 영향을 받는다. ^[57] 이 현상은 음향파의 비선형 상호작용에 의해 야기되며, 사실 그 계획은 시간에 명시되어 있고 우주에 집중되어 있다.^[58]

몇 년 동안, 이 문제를 없애기 위해 몇 가지 기술이 제안되었다. 그들은 세 개의 다른 그룹으로 분류될 수 있다.

1. 밀도 필터를 채택하는 계획,
2. 연속성 방정식에 분산 항을 추가하는 모델,
3. 입자 상호작용을 모델링하기 위해 리만 솔버를 사용하는 계획들

밀도 필터 기법

첫 번째 그룹의 계획은 필터를 밀도 필드에 직접 적용하여 가짜 수치 노이즈를 제거한다. 가장 많이 사용되는 필터는 MLS(이동 최소 사각형)와 쉐퍼드 필터로, 각 시간 단계 또는 n 시간 단계에서 적용할 수 있다. 필터링 절차의 사용 빈도가 높을수록 규칙적인 밀도와 압력장을 얻는다. 반면에, 이것은 계산 비용의 증가로 이어진다. 장기간 시뮬레이션에서 필터링 절차를 사용하면 정수압 구성 요소의 중단과 전지구 유체 부피와 밀도 장 사이의 불일치로 이어질 수 있다. 또한 동적 자유 표면 경계 조건의 시행을 보장하지 않는다.

확산용어기법

밀도와 압력장을 매끄럽게 하는 다른 방법은 연속성 방정식(그룹 2) 내부에 확산성 용어를 추가하는 것이다.

${\displaystyle {\displaystyle {\frac {d\rho _{i}}{dt}}=\sum _{j}m_{j}\left({\boldsymbol {v}}_{i}-{\boldsymbol {v}}_{j}\right)\cdot \nabla W_{ij}+{\mathcal {D}}_{i}(\rho ),}}$

그러한 접근법을 채택한 첫 번째 계획은 페라리 및 확산 용어가 밀도 영역의 라플라시아어로 모델링된 몰테니에서^[56] 설명되었다. 비슷한 접근법이 파티와 만자리에서도 사용되었다.^[60]

Antuono 등에서는 자유표면에 가까운 일부 불일치를 제거하기 위해 Molteni의^[56] 확산 용어에 대한 보정이 제안되었다. 이 경우 채택된 확산 용어는 밀도 분야에서 고차 미분 연산자와 동등하다.^[62] 이 계획은 Δ-SPH라고 불리며, 확산 없이 SPH의 모든 보존 특성(예: 선형 및 각도 모멘트, 총 에너지, 참조)^[63]을 보존하고 밀도와 압력장을 부드럽고 규칙적으로 표현한다.

세 번째 그룹에는 입자 상호작용을 모델링하기 위해 Riemann 솔버를 통해 얻은 숫자의 플럭스를 사용하는 SPH 체계가 있다.^[64][65][66]

리만 해결사 기법

For an SPH method based on Riemann solvers, an inter-particle Riemann problem is constructed along a unit vector ${\displaystyle {\mathbf {e}}_{ij}=-{\mathbf {r}}_{ij}/r_{ij}}$ pointing form particle ${\displaystyle i}$ to particle ${\displaystyle j}$. In this Riemann problem the i질소 왼쪽 및 오른쪽 상태는 각각 $입자{\displaystyle }$ i ${\displaystyle i}$ $및$ j ${\displaystyle j}$에 있다.$$ $L{\displaystyle }$ ${\displaystyle L}$ 및$$ $R{\displaystyle }$ ${\displaystyle R}$ 상태는$$

${\displaystyle {\begin{cases}(\rho _{L},U_{L},P_{L})=(\rho _{i},{\mathbf {v}}_{i}\cdot {\mathbf {e}}_{ij},P_{i})\\(\rho _{R},U_{R},P_{R})=(\rho _{j},{\mathbf {v}}_{j}\cdot {\mathbf {e}}_{ij},P_{j}).\end{case}}$

리만 문제의 해결은 불연속성에서 나오는 세 파장을 낳는다. 충격파나 희박파일 수 있는 두 개의 파동은 가장 작거나 가장 큰 파속력으로 이동한다. The middle wave is always a contact discontinuity and separates two intermediate states, denoted by ${\displaystyle (\rho _{L}^{\ast },U_{L}^{\ast },P_{L}^{\ast })}$ and ${\displaystyle (\rho _{R}^{\ast },U_{R}^{\ast },P_{R}^{\ast })}$. By assuming that the intermediate state satisfies ${\displaystyle U_{L}^{\ast }=U_{R}^{\ast }=U^{\ast }}$ and ${\displaystyle P_{L}^{\ast }=P_{R}^{\ast }=P^{\ast }}$, a linearized Riemann solver for smooth flows or with only moderately strong shocks can be written as

${\displaystyle {\displaysty}U^{\ast }={\overline {U}+{\frac {1}{1}:{2}}: {\frac {(P_{L}-P_{R}}}}{\bar {\\rho }}}}\P^{\ast }={\overline{P}+{\frac {1}{1}:{2}}:{\bar {\rho }}}{{0}{(U_{L}-U_{R}}}}}}}},\case}}}}}}}$

where ${\displaystyle {\overline {U}}=(U_{L}+U_{R})/2}$ and ${\displaystyle {\overline {P}}=(P_{L}+P_{R})/2}$ are inter-particle averages. 리만 문제 해결로, 다시 말해서. ${\displaystyle U^{}}$$∗{\$ $P{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}${\$displaystyle$ P$^{\ast$ $\}\},$ SPH 방법의 디스커트화는

${\dfrac{d\rho_{dt}=2\rho_{i}}{j}{\frac{m_{j}{\rho_{j}}}({\mathbf{v}-{v}-{\mathbf{v}^{\ast }}}}\cdot \cdla _{i}}}}W_{ij}}$

${\dfrac{\mathbf{v}_{i}}{dt}=-2\sum _{j}{j}{j}{\bigg (}{\frac {P^{\ast }}}{\rho _{j}}}{j}}}}\nabla _{i}}W_{ij}}$

where ${\displaystyle {\mathbf {v}}^{\ast }=U^{\ast }{\mathbf {e}}_{ij}+({\overline {\mathbf {v}}}_{ij}-{\overline {U}}{\mathbf {e}}_{ij})}$. 이는 입자간 평균 속도와 압력이 단순히 리만 문제의 해결책으로 대체된다는 것을 나타낸다. 이 둘을 비교함으로써 입자간 평균에서 나오는 중간 속도와 압력은 각각 밀도 정규화와 수치 점도와 같은 암묵적 소산에 해당한다는 것을 알 수 있다.

위의 디스트리뷰테이션은 매우 소멸적이기 때문에 간단한 수정은 다음과 같이 중간 압력을 제한함으로써 도입된 암묵적 수치 소멸을 줄이기 위한 제한장치를 적용하는 것이다.

${\displaystyle P^{\ast }={\overline{P}+{\frac {1}{1}:{2}}:\beta{\overline{\rho}}}}{{(U_{L}-U_{R}}}}}}}}}}},}}$

제한 장치가 다음과 같이 정의되는 경우

${\displaystyle \beta =\min {\big(}\eta \max(U_{L}-U_{R},0),{\overline {c}{\big )}.}$

$\beta {\displaystyle }$ ${\displaystyle \beta }$은(는) 유체가 팽창 파형의 작용 하에 있을 때, 즉, 소산되지 않도록 보장한다는$$ 점에 유의하십시오. < R ${\$ 및 이 매개 변수 η ${\displaystyle \eta }$은$$유체가 압축파의 작용 아래에 있을 때 방산을 변조하는 데 사용된다. ${\displaystyle U_{}}$ ${\displaystyle L_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle R_{}}$ ${\$수치 실험 결과 ${\displaystyle \mathrm{\eta }}$= 3 ${\displaystyle \eta =3}$이(가) 일반적으로$$ 효과가 있는 것으로 나타났다. 또한 중속도에 의해 유입되는 소산은 제한되지 않는다는 점에 유의한다.

압축할 수 없는 접근법

점도 모델링

일반적으로 유체역학적 흐름에 대한 설명은 Navier의 점도를 모델링하기 위한 확산 과정의 편리한 처리가 필요하다.-스토크 방정식. 그것은 라플라시안 차동 운영자를 포함하기 때문에 특별한 고려가 필요하다. 직접 연산은 만족스러운 결과를 제공하지 못하기 때문에 확산 모델링을 위한 몇 가지 접근법이 제안되었다.

• 인공 점도

모나한과 진골드에 의해 소개된 인공 점도는 높은 마하 수 유체 흐름을 다루기 위해 사용되었다. 라고 쓰여 있다.

${\displaystyle \Pi _{ij}={\begin{cases}{\dfrac {-\alpha {\bar {c}}_{ij}\phi _{ij}+\beta \phi _{ij}^{2}}{{\bar {\rho }}_{ij}}}&\quad {\boldsymbol {v}}_{ij}\cdot {\boldsymbol {r}}_{ij}<0\\0&\quad {\boldsymbol {v}}_{ij}\cdot {\boldsymbol {r}}_{ij}\geq 0\end{cases}}}$

여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$이(가) 볼륨 점도를 제어하는 반면$$ $\beta {\displaystyle }$ ${\displaystyle \beta$ }은$($는) Neumann Richtmeyr 인공 점도와 유사하게 작용한다$$. $\varphi {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$은(는) 다음에 의해 정의된다$$.

${\displaystyle \phi_{ij}={\frac {h{\boldsymbol{v}_{ij}\cdot{\boldsymbol{r}}}}{ij}}}{\vert {\boldsymbol{r}}}\{2}+\e}}}}}}}}.}$

인공 점도는 또한 일반적인 흐름 시뮬레이션의 전반적인 안정성을 향상시키는 것을 보여주었다. 따라서, 다음과 같은 형태로 불시의 문제에 적용한다.

${\displaystyle \Pi_{ij}=\알파 hc{\frac {{\boldsymbol{v}}}{ij}}}\cdot{\boldsymbol{r}}}}}{ij}}}{{ij}}}}}}\vert{{{{2}+\eta}}}}}}.}$

이 접근방식에 의해 비실시적 시뮬레이션을 안정화할 뿐만 아니라 물리적 점도를 모델링하는 것도 가능하다. 그렇게 하기 위해서

${\displaystyle \c=2(n+2){\frac {\mu}{\rho}}}}$

위의 방정식에서 대체되며, $여기$서 n ${\displaystyle n}$은(는) 모델의 스페어 치수의 수입니다. 이 접근방식은 대량 $점성{\displaystyle }$ ${\displaystyle =}$ = ${\displaystyle 5\frac{\mathrm{}}{}}$ ${\displaystyle 3\mu }$ ${\displaystyle \zeta ={\frac$ {$5}{3}}\mu }$을(를) 도입한다$.$

• 모리스

낮은 레이놀즈 숫자의 경우 모리스의 점성 모델이 제안되었다.

${\displaystyle [\nu \Delta {\boldsymbol {v}}]_{ij}={\frac {2\nu }{\rho _{j}}}\,{\frac {{\boldsymbol {r}}_{ij}\cdot \nabla w_{h,ij}}{\Vert {\boldsymbol {r}}_{ij}\Vert ^{2}+\eta _{h}^{2}}}\,{\boldsymbol {v}}_{ij}.}$

• 로사오

추가물리학

• 표면장력
• 열전달
• 난류

다중 경로 확장

천체물리학

종종 천체물리학에서는 순수한 수력역학 외에 자기중력을 모형화하기를 원한다. SPH의 입자 기반 특성은 예를 들어 나무 중력 코드,^[70] 입자 메쉬 또는 입자 입자 입자 메쉬와 결합하는 것을 이상적으로 만든다.

고체 역학과 유체 구조 상호작용(FSI)

고체 역학을 위한 총 라그랑어 공식

고체 역학의 지배 방정식을 분간하기 위해, 수정 행렬 ${\displaystyle {\mathrm{}}^{}}$ 0 ${\$이(가) 먼저 도입되어$$^[71][72] 강체-신체 회전을 다음과 같이 재현한다.

${\displaystyle \mathbb {B} _{a}^{0}=\left(\sum _{b}V_{b}^{0}\left(\mathbf {r} _{b}^{0}-\mathbf {r} _{a}^{0}\right)\otimes \nabla _{a}^{0}W_{ab}\right)^{-1}}$

(1)

어디에

$\displaystyle \nabla _{a}^{0}W_{a}={\frac {\partial W\left(\mathbf {r} _{ab}^{0},h\right)}{\partial \mathbf {r} _{ab}^{0}}}}}}{ab}^{ab}^{0}}}}}}}}}}}}}}}}}}$

초기 기준 구성에서 평가된 커널 함수의 그라데이션이다. $고형{\displaystyle }$ 입자를 나타내기 위해 $첨자$ a {\$displaystyle$ a} 및 b {\displaystyle $b}$이$($가$)$ 사용되며$$, 평활 $길이{\displaystyle }$ h$${\$displaystyle h$}은(는) 유체 방정식의 변위법과 동일하다는 점에$$ 유의하십시오.

초기 구성을 기준으로 하여 고체 밀도를 직접 평가한다.

${\displaystyle \rho_{a}=\rho_{a}^{0}{\frac{1}{J}}}$

(2)

여기서 $J{\displaystyle }$= ${\displaystyle det}$(${\displaystyle F\mathbb{}}$) ${\displaystyle$ J$=\det(\mathb {F} )}$은 변형 텐서 $F{\displaystyle \mathbb{}}$ ${\$의 Jacobian 결정 요인이다$.$

이제 다음 형태로 모멘텀 방정식을 확인할 수 있다.

${\displaystyle m_{a}{\frac {{\text{d}}\mathbf {v} }{{\text{d}}t}}=2\sum _{b}V_{a}V_{b}{\tilde {\mathbb {P} }}_{ab}\nabla _{a}^{0}W_{ab}+\mathbf {g} +\mathbf {f} _{a}^{F:p}+\mathbf {f} _{a}^{F:v}}$

(3)

여기서 입자간 평균은 첫 번째 Piola-Kirchhoff 스트레스 $P{\displaystyle \stackrel{}{\mathbb{}}}$~ ${\$로 정의된다.

${\displaystyle {\tilde {\mathb {P}}}}{{ab}={\frac {1}{1}{1}{1}}\좌측(\mathb {P} _{a}\mathb {B}+{b}\mathb {B}_{B}\mathb}^{0}\우측).}$

(4)

또한$$ ${\displaystyle {}_{}^{}}$: ${\displaystyle p_{}^{}}$ ${\$$displaystyle \mathbf {f} _{a}^{F:p}$ 및$$ $f{\displaystyle {\mathbf{}}_{}^{}}$: ${\displaystyle v_{}^{}}$ ${\$ {f$} _{a}^{F:v$$\}$는 각각 고체 입자 a}에 작용하는 유체 $압력과 점성력$에 해당한다.

유체-구조 커플링

유체 구조 커플링에서 주변 고체 구조물은 유체의 이동 경계로 작용하고 있으며, 유체 구조 인터페이스에서 미끄럼 방지 경계 조건이 부과된다. ${\displaystyle {}_{}^{}}$한 고체 $입자{\displaystyle }$ a ${\displaystyle$ a$}$의 존재로 인해 p {\$displaystyle$ $\mathbf$$${$f} _{i}^{S:v}$ 및$$ ${\displaystyle {}_{}^{}}$ S :${\displaystyle v_{}^{}}$ ${\$$displaystyle i}$에 작용하는$$ 상호작용 힘은 {\displaystystyle a}$$로 얻을 수 있다$.$

${\displaystyle \mathbf {f} _{i}^{S:p}=-2\sum _{a}V_{i}V_{a}{\frac {p_{i}\rho _{a}^{d}+p_{a}^{d}\rho _{i}}{\rho _{i}+\rho _{a}^{d}}}\nabla _{i}W(\mathbf {r} _{ia},h)}$

(5)

그리고

${\displaystyle \mathbf {f} _{i}^{S:v}=2\sum _{a}\eta V_{i}V_{a}{\frac {\mathbf {v} _{i}-\mathbf {v} _{a}^{d}}{r_{ia}}}{\frac {\partial W(\mathbf {r} _{ia},h)}{\partial {{r}_{ia}}}}.}$

(6)

여기서 상상압력 p a ${\displaystyle {}_{}^{}}$ ${\$ 및 ${\displaystyle {}_{}^{}}$ v ${\displaystyle {}_{}^{}}$ d$${\$displaystyle \mathbf {v} _{a}^{d}}$는 다음과 같이 정의된다$$.

${\displaystyle {\begin{cases}p_{a}^{d}=p_{i}+\rho _{i}\max(0,(\mathbf {g} -{\frac {{\text{d}}\mathbf {v} _{a}}{{\text{d}}t}})\cdot \mathbf {n} ^{S})(\mathbf {r} _{ia}\cdot \mathbf {n} ^{S})\\\mathbf {v} _{a}^{d}=2\mathbf {v} _{i}-\mathbf {v} _{a}.\end{case}}}$

(7)

여기서 $n{\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}$ ${\$는 고체 구조의 표면 정상 방향을 나타내며$$, 가상의 입자 밀도 $\rho {\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$는 상태의 방정식을 통해 계산된다$$.

$따라서$, $f{\displaystyle {\mathbf{}}_{}^{}}$: ${\displaystyle p_{}^{}}$ ${\displaystyle$ $\mathbf {f} _{a}^{F:p}$ 및$$ ${\displaystyle {}_{}^{}}$: ${\displaystyle v_{}^{}}$ ${\$$}}$가 $부여$한 고체$$ 입자에 작용한다$$.

${\displaystyle \mathbf {f} _{a}^{F:p}=-2\sum _{i}V_{a}V_{i}{\frac {p_{a}^{d}\rho _{i}+p_{i}\rho _{a}^{d}}{\rho _{i}+\rho _{a}^{d}}}\nabla _{a}W(\mathbf {r} _{ai},h)}$

(8)

그리고

${\displaystyle \mathbf {f} _{a}^{F:v}=2\sum _{i}\eta V_{a}V_{i}{\frac {\mathbf {v} _{a}^{d}-\mathbf {v} _{i}}{r_{ia}}}{\frac {\partial W(\mathbf {r} _{ia},h)}{\partial {{r}_{ai}}}}.}$

(9)

커널 함수의 파생상품에 대한 반대칭 특성은 상호작용하는 $입자{\displaystyle }$ i ${\displaystyle i}$와$${\$displaystyle a}$의 각 쌍에 대한 모멘텀 보존을 보장할 것이다$.$

다른이들

세분화된 물질을 시뮬레이션하는 데 사용되는 이산 요소 방법은 SPH와 관련이 있다.

방법의 변형

이 구간은 비어 있다. 추가하면 도움이 된다.(2018년 7월)

참조

추가 읽기

• 후버, W. G. (2006) 부드러운 입자 적용 역학: 세계 과학, 예술의 상태
• SPH Stelingwerf, R. F., Wingate, C. A., Memorie deella Societa Cosmitalia Italiana, Vol. 65, 페이지 1117(1994)로 충격 모델링.
• 아마다, T, 이무라, M, 야스무로, Y, 마나베, Y, 치하라(2004) GPU에 대한 입자 기반 유체 시뮬레이션(2004년 8월, 캘리포니아 주 로스앤젤레스, 범용 컴퓨팅에 관한 ACM 워크샵 진행)
• 데스브룬, M.과 카니, M-P. (1996년) 평활 입자: 매우 변형 가능한 신체에 활기를 불어넣기 위한 새로운 패러다임. 컴퓨터 애니메이션과 시뮬레이션에 관한 유로그래픽스 워크숍(1996년 8월, 프랑스 푸아티에)에서.
• 헤겔만, K, Car, N.A.와 밀러, G.S.P. 입자 기반 유체 시뮬레이션 GPU.In International Conference of Computing Science (Reading, UK, 2006년 5월) 컴퓨터 과학 대 3994/2006년에 강의 노트(Springer-Verlag)로 발행된 절차.
• M. 켈라거 (2006) 평활입자 수력역학, M. 켈라가르(MS논문, Univ)를 이용한 라그랑기 유체역학 코펜하겐).
• 코브, A, 쿤츠, N. (2005) GPU 기반 유체 시뮬레이션을 위한 동적 입자 커플링 제18회 시뮬레이션 기법 심포지엄(2005) 페이지 722-727.
• 류, G.R., 류, M.B. 평활입자 수역학: 메쉬 없는 입자법. 싱가포르: 월드 사이언티픽(2003년).
• 모나한, J.J. (1992년). 평활 입자 수역학. 안누. 우주 비행사 목사님. 천체. (1992년) 30 : 543–74.
• 컴퓨터 애니메이션에 관한 Eurographics/SIGGRAP 심포지엄(2003)에서 Muller, M, Charypar, D. and Gross, M. 입자 기반 유체 시뮬레이션. D. 브린과 M. 린.
• Vesterlund, M. 평활 입자 수역학을 이용한 점성 유체의 시뮬레이션 및 렌더링(MS Statement, Umea University, 스웨덴)
• Violeau, D, Fluid Mechanics 및 SPH 방법. 옥스퍼드 대학 출판부(2012년).

외부 링크

• SPH를 이용한 항성 형성의 첫 번째 대규모 시뮬레이션
• SPERE(SPH research and engineeRing International Community)
• ITVO는 수치 시뮬레이션 아카이브의 데이터베이스를 조회하기 위해 만들어진 이탈리아 이론 가상 천문대의 웹 사이트다.
• SPHC 이미지 갤러리에는 SPH 코드 SPHC의 다양한 테스트 사례, 실험 검증 및 상업적 용도가 묘사되어 있다.
• Navier-Stokes 방정식에서 시작되는 SPH 모델의 파생

소프트웨어

• 알고두는 SPH를 이용한 교육을 위한 2D 시뮬레이션 프레임워크다.
• AQUAgupusph는 연구자들이 연구자들에게 무료로 제공하는 (GPLv3) SPH이다.
• 다이브 솔루션은 CFD 목적을 위한 상용 웹 기반 SPH 엔지니어링 소프트웨어다.
• 듀얼SPHysics는 주로 SPHysics를 기반으로 GPU 컴퓨팅을 사용하는 오픈 소스 SPH 코드다. 오픈 소스 부품은 LGPL에서 사용할 수 있다.
• FLUIDS v.1은 CPU 및 GPU용 액체를 C+++로 실시간 3D SPH 구현하는 간편한 오픈 소스(Zlib)이다.
• Fluidix는 OneZero 소프트웨어에서 사용할 수 있는 GPU 기반 입자 시뮬레이션 API이다.
• GAGET [1]은 우주론 N-body/SPH 시뮬레이션을 위해 자유롭게 사용할 수 있는 (GPL) 코드다.
• 점도가 있는 GPUSPH SPH 시뮬레이터(GPLv3)
• 파시모도는 입자 기반 시뮬레이션 방법(예: SPH)을 위한 프로그램 패키지다.
• 물리 추상화 레이어는 SPH 지원으로 실시간 물리 엔진을 지원하는 오픈소스 추상화 시스템이다.
• PreonLab은 502 Technology가 암묵적 SPH 방법을 구현하여 개발한 상용 엔지니어링 소프트웨어다.
• Punto는 입자 시뮬레이션을 위해 자유롭게 사용할 수 있는 시각화 도구다.
• Python에서 Smoothed Particle Hydrodynamics를 위한 Pysph 오픈 소스 프레임워크 (New BSD License)
• RealFlow Commercial SPH 해결사 영화 산업용.
• RheoCube는 전자안트랩의 상용 SaaS 제품으로, 마이크로스케일 MD 시뮬레이션을 통해 중시경 SPH 모델을 결합한 제품이다.
• SimPARTIX는 프라운호퍼 IWM의 SPH 및 이산요소법(DEM) 시뮬레이션을 위한 상용 시뮬레이션 패키지다.
• SPH-흐름
• 스페라
• SPHinXsys는 오픈 소스 다중 물리학, 다중 해상도 SPH 라이브러리 입니다. 물리적 정밀한 시뮬레이션을 위한 C++ API를 제공하고, 유체, 고체, 다체역학 등을 포함한 결합된 산업역학 시스템의 모델링을 목표로 한다.
• SPHysics는 Fortran에서 오픈 소스 SPH 구현
• SPLASH는 SPH 시뮬레이션을 위한 오픈 소스(GPL) 시각화 툴이다.
• SYMPER: 프리부르크 대학의 프리웨어 SYMbolic Spitle SimulatoR.
• Nauticle은 입자 기반 수치법을 위한 범용 계산 툴이다.