쇼어 알고리즘

쇼어의 알고리즘은 정수의 소인수를 구하는 양자 알고리즘입니다. 1994년 미국 수학자 피터 쇼어에 의해 개발되었습니다.^[1][2] 그것은 가장 잘 알려진 고전적(즉, 비양자적) 알고리즘에 비해 강력한 잠재적 응용과 다항 속도 향상의 강력한 증거를 가진 몇 안 되는 알려진 양자 알고리듬 중 하나입니다.^[3] 반면에 실질적인 중요성의 수를 인수분해하려면 가까운 미래에 사용할 수 있는 큐비트보다 훨씬 더 많은 큐비트가 필요합니다.^[4] 또 다른 우려는 양자 회로의 노이즈가 결과를 손상시킬 ^[5]수 있어 양자 오류 수정을 위해 추가 큐비트가 필요하다는 것입니다.

Shor는 인수분해 문제, 이산 로그 문제, 주기 찾기 문제를 해결하는 유사한 알고리즘을 여러 개 제안했습니다. "쇼어의 알고리즘"은 보통 그의 알고리즘이 인수분해를 해결하는 것을 언급하지만, 세 가지를 각각 언급할 수도 있습니다. 이산 로그 알고리즘과 인수분해 알고리즘은 기간 찾기 알고리즘의 예이며, 세 가지 모두 숨겨진 부분군 문제의 예입니다.

양자 컴퓨터에서 정수 $N$ ${\displaystyle$ N$}$을 인수분해하기$$위해 Shor의 알고리즘은 다항식 시간으로 실행되며, 이는 입력으로 주어진 정수의 크기인 $로그$⁡ N ${\displaystyle$ \log N}에서 소요되는 시간이 다항식임을 의미합니다. 구체적으로, $순서$ ${\displaystyle O^{}}$(로그 ⁡ N${\displaystyle )}$ ${\displaystyle 2}$(${\displaystyle \mathrm{로그}}$ ⁡ $로그$⁡ N)의 양자 ${\displaystyle \mathrm{게이트}}$(로그${\displaystyle }$⁡ $로그$ ⁡ N)를 취합니다. {\display O\!빠른 곱셈을 사용하여$\left((\log$ N$)^{2}(\log \log$ N$)(\log \log N)\right)}$ 또는 심지어 $O{\displaystyle ((({로그}^{}}$ $⁡$ ${\displaystyle N}$)${\displaystyle }$2(${\displaystyle 로그}$ $⁡$ $로그$ $⁡$ N)) {\display O\!하비와 반 더 호벤으로 인해 현재 알려진 가장 빠른 곱셈 알고리즘을 활용하여$\left((\log N)^{2}(\log \log N)\right)},$^[8] 따라서 정수 인수분해 문제가 양자 컴퓨터에서 효율적으로 해결될 수 있으며 결과적으로 복잡도 클래스 BQP에 있음을 보여줍니다. 이는 하위 지수 시간에서 작동하는 가장 효율적인 알려진 고전적 인수분해 알고리즘인 일반 숫자 $필드$ 체보다 훨씬 빠릅니다:${\displaystyle }$O (e ${\displaystyle {.9}^{}}$ ${\displaystyle {({로그}^{}}^{}}$ ⁡${\displaystyle {N^{}}^{}}$) 1 / 3 (로그 ⁡ $로그$ ⁡ N ) 2 / 3 ) {\display O\!$\left(e^{1.9(\log N)^{1/3}(\log \log N)^{2/3}}\right)}$.^[9]

실현가능성 및 영향

충분한 수의 큐비트를 가진 양자 컴퓨터가 양자 잡음 및 기타 양자 결맞음 현상에 굴복하지 않고 작동할 수 있다면 쇼어의 알고리즘을 사용하여 다음과 같은 공개 키 암호 체계를 깰 수 있습니다.

• RSA 스킴
• 유한장 디피-헬만 키 교환
• 타원 곡선 디피-헬만 키 교환^[10]

RSA는 큰 정수를 인수분해하는 것이 계산상 다루기 어렵다는 가정을 기반으로 합니다. 알려진 바로는, 이 가정은 고전적인 (양자가 아닌) 컴퓨터에 유효합니다. 다항 시간에 정수를 인수분해할 수 있는 고전적인 알고리즘은 알려져 있지 않습니다. 그러나 Shor의 알고리즘은 이상적인 양자 컴퓨터에서 정수를 인수분해하는 것이 효율적이므로 큰 양자 컴퓨터를 구축하여 RSA를 물리치는 것이 가능할 수 있음을 보여줍니다. 또한 양자 컴퓨터의 설계와 구축, 새로운 양자 컴퓨터 알고리즘 연구에 강력한 동기부여가 되었습니다. 또한 양자 컴퓨터로부터 안전한 새로운 암호 시스템에 대한 연구를 촉진했으며, 이를 총칭하여 포스트 양자 암호학이라고 합니다.

물리적 구현

현대 양자 컴퓨터의 높은 오류율과 양자 오류 수정을 사용하기에 너무 적은 큐비트를 감안할 때, 실험실 시연은 극히 일부의 시도에서만 정확한 결과를 얻습니다.

2001년 IBM의 그룹은 7 큐비트의 양자 컴퓨터의 NMR 구현을$$사용하여 ${\displaystyle$ $15{\displaystyle \mathrm{}\}}$를 3$$× 5 {\$displaystyle 3\times 5}$로 분리하여 쇼어의 알고리즘을 입증했습니다.^[11] IBM의 구현 이후 두 개의 독립적인 그룹이 포토닉 큐비트를 이용한 쇼어 알고리즘을 구현하면서 쇼어 알고리즘 회로를 구동할 때 다중 큐비트 얽힘이 관찰되었음을 강조했습니다.^[12][13] 2012년에는 솔리드 스테이트 큐비트를 ${\displaystyle \mathrm{사용}}$하여 15 {\$displaystyle$ 15$}$의 인수분해가$$ 수행되었습니다$.$^[14] 이후 2012년에는 ${\displaystyle 21}$ ${\displaystyle 21}$의 인수분해를 달성했습니다$$.^[15] 2019년 IBM Q System One에서 Shor의 알고리즘을 사용하여$$ 숫자 ${\displaystyle 35}$ ${\displaystyle 35}$를 인수분해하려고 시도했지만 오류가 누적되어 알고리즘에 실패했습니다.^[16] 양자 컴퓨터가 다른 알고리즘을 사용하여 더 큰 수를 인수분해했지만,^[17] 이러한 알고리즘은 요인의 고전적인 단순한 검사와 유사하므로 쇼어의 알고리즘과 달리 고전적 인수분해 알고리즘보다 더 나은 성능을 발휘하지 못할 것으로 예상됩니다.^[18]

쇼어 알고리즘의 이론적 분석은 잡음과 오류가 없는 양자 컴퓨터를 가정합니다. 그러나 단기적인 실제 구현은 그러한 원치 않는 현상을 처리해야 합니다(더 많은 큐비트를 사용할 수 있을 때 양자 오류 수정이 도움이 될 수 있습니다). 2023년 진이 카이(Jin-Yi Cai)는 노이즈의 영향을 연구하고 특수한 종류의 숫자(반 소수에 밀도가 높은 A073024의 두 소수의 곱)가 있다고 결론지었습니다. 쇼어의 알고리즘은 노이즈가 있는 경우 이러한 숫자를 인수분해할 수 없습니다.^[5] 따라서 모든 숫자를 Shor의 알고리즘으로 인수분해할 수 있으려면 오류 수정이 필요합니다.

알고리즘.

우리가 풀려고 하는 문제는 홀수 합성수 $N{\displaystyle }$ ${\displaystyle$ N$}$이 주어졌을 때$,$ 그 정수 인자를 찾는 것입니다.

이를 달성하기 위해 쇼어의 알고리즘은 두 부분으로 구성됩니다.

1. 인수분해 문제를 순서 찾기 문제로 고전적으로 축소한 것입니다. 이 감소는 2차 체와 같은 다른 인수분해 알고리즘에 사용되는 것과 유사합니다.
2. 순서 찾기 문제를 해결하기 위한 양자 알고리즘입니다.

고전적 축소

임의의 $N{\displaystyle }$ ${\displaystyle N}$을 1보다$$ 큰 두 정수 $p{\displaystyle }$ ${\displaystyle$ p$}$와 $q{\displaystyle }$ ${\displaystyle q}$로 효율적으로 인수분해할 수 있다면 완전 인수분해 알고리즘이 가능합니다. $p{\displaystyle }$ ${\displaystyle p}$ 또는$$ $q{\displaystyle }$ ${\displaystyle q}$ 중 하나가 소수가$$ 아닌 경우 소수만 남을 때까지 인수분해 알고리즘을 차례로 실행할 수 있습니다.

기본적인 관찰은 유클리드의 알고리즘을 사용하면 항상 두 정수 사이의 GCD를 효율적으로 계산할 수 있다는 것입니다. 특히 $N{\displaystyle }$ ${\displaystyle$ N$}$이(가) 짝수인지 여부를 효율적으로 확인할 수 있으며, 이 경우 2는 사소한 요인입니다. $따라서{\displaystyle }$ 이 논의의 나머지 부분에서 N ${\displaystyle$ N$}$이 홀수라고 가정합니다. 그런 다음 효율적인 고전 알고리즘을 사용하여 $N{\displaystyle }$ ${\displaystyle N}$이 소수인지 확인할 수 있습니다.^[19] 소수의 경우 효율적인 고전적 인수분해 알고리즘이 ^[20]존재하므로 나머지 양자 알고리즘은 $N{\displaystyle }$ ${\displaystyle N}$이 소수가 아니라고$$ 가정할 수 있습니다.

이러한 쉬운 케이스가 $N{\displaystyle }$ ${\displaystyle N}$의 사소한 인자를 생성하지 않는 경우 알고리즘은 나머지 케이스를 처리하기 위해 진행합니다$.$ 저희는 무작위 2≤ < {\$displaystyle 2\leqa< N}$을 선택합니다 N$${\$displaystyle$N}의 가능한 비자분수는 유클리드 알고리즘을 사용하여 고전적이고 효율적으로 수행할 수 있는$$${\displaystyle gcd(a,}$ ${\displaystyle N)}$ ${\displaystyle \gcd(a,$ N$)}$를 계산하여 $찾을{\displaystyle }$ 수 있습니다$$. 이것이 사소하지 않은 인자(${\displaystyle gcd(a,}$ ${\displaystyle N))}$를 생성하는 경우 ≠ 1 {\$displaystyle \gcd$(a, N)\n$eq 1}),$ 알고리즘이 완료되었으며, 다른 비소용 인자는 $\frac{Ngcd(a,}{}$ N$\frac{)}{}$ ${\$ N$)}}$입니다$.$ 비소용 인자가 식별되지 않은 경우, $이$는 N$${\$displaystyle$N}과$${\$displaystyle$ a$}$의 선택이$$ 코프라임임을 의미합니다. 여기서 알고리즘은 양자 서브루틴을 실행하여 ${\display a}$의 $순서{\displaystyle }$ ${\displaystyle r}$을(를) 반환합니다$.$ 이는 다음을 의미합니다.

${\displaystyle a^{r}\equiv 1{\bmod {N}}.$

양자 서브루틴은 ${\displaystyle$ a$}$ 및 N ${\displaystyle N}$이(가) 코프림이어야 하며,^[2] 이는 알고리즘의 이 시점에서 ${\displaystyle gcd(a,}$ N${\displaystyle )}${\$displaystyle \gcd(a, N)}$가 N$${\$displaystyle$N}의 $사소한$ 인자를 생성하지$$ 않았기 때문에 사실입니다$.$ $N$ ${\displaystyle N}$이${\displaystyle {}^{}}$가) ${\displaystyle \mathrm{r}}$- 1 {\$displaystyle a^{r$1$}$을 ${\displaystyle \mathrm{분할}}$하고$$N ∣ r - 1${\displaystyle N$mid a^{r}-1}로 쓴 것을 동등성에서 확인할 수 있습니다. 이는 제곱의 차이를 사용하여 인수분해할 수 있습니다.

이러한 방식으로 식을 인수분해했기 때문에 알고리즘이 홀수 $r${\$display$r}($$${\displaystyle {ar}^{}}$ ${\displaystyle {/}^{}}$ ${\displaystyle {2\mathrm{}}^{}}${\$display a^{r/2}}$가 정수여야$$ 하므로)에 대해 작동하지 않습니다$.$ 즉, 알고리즘이 $새{\displaystyle }${\$displaystyle$a}로 다시 시작해야 합니다. 따라서 $이후$에는 r ${\display r}$이 짝수라고 가정할 수 있습니다. It cannot be the case that ${\displaystyle N\mid a^{r/2}-1}$, since this would imply ${\displaystyle a^{r/2}\equiv 1{\bmod {N}}}$, which would contradictorily imply that ${\textstyle {\frac {r}{2}}}$ would be the order of ${\displaystyle a}$, 이미 $r$ ${\displayr}$ 이었습니다$.$ 이때 ${\displaystyle N^{}}$ ∣${\displaystyle \mathrm{ar}}$ / 2 + $1$ ${\displaystyle N\mida^{$r$/$2}+1}일 수도 있고 아닐 수도 있습니다. ${\displaystyle N^{}}$ ∣${\displaystyle \mathrm{ar}}$ / 2 + $1$ ${\displaystyle N\mid a^{$r$/$2}+1}이 참이 아니면 N ${\displaystyle$N}의 사소$인자$를 찾을 수 있습니다.If ${\displaystyle d=1}$, then that means ${\displaystyle N\mid a^{r/2}+1}$ was true, and a nontrivial factor of ${\displaystyle N}$ cannot be achieved from ${\displaystyle a}$, and the algorithm must restart with a new ${\displaystyle a}$. Otherwise, $N{\displaystyle }$ ${\displaystyle N}$의 사소한 인자를 찾았고$,$ 다른 인자는 $\frac{\mathrm{Nd}}{}$ ${\$이며$,$ 알고리즘은 완료되었습니다. 이 단계에서는 ${\displaystyle gcd(N,}$ ${\displaystyle {ar}^{}}$${\displaystyle {}^{}}$/ ${\displaystyle 2^{}}$+ ${\displaystyle 1)}$ ${\displaystyle \gcd(N,a^{r/2}+1)}$를 계산하는 것과 동일하며$,$ ${\displaystyle gcd(N,}$ ${\displaystyle {ar}^{}}$ ${\displaystyle {/}^{}}$2 -${\displaystyle 1}$)$${\$displaystyle \gcd(N,a^{r/2}-1)}$가 사소한 경우 사소한 인자를 생성하지 않습니다(여기서 $N$ ∣${\displaystyle \mathrm{ar}{}^{}}$/$$2 + 1${\displaystyle N\mid a^{$r/2}+1}).

알고리즘은 곧 다음과 같이 재작성되었습니다. $N{\displaystyle }$ ${\displaystyle$ N$}$은(는) 소수가 아니라 홀수입니다. $N{\displaystyle }$ ${\displaystyle N}$의 두 개의 사소한 인자를 출력하고자 합니다$.$

이것은 몇 번의 주행 후에 성공할 가능성이 있는 것으로 나타났습니다.^[2] 실제로 양자 순서 찾기 서브루틴에 대한 한 번의 호출만으로도 N ${\displaystyle N}$을 매우 높은 성공 확률로 완전히 인수분해하기에 충분합니다.^[21]

양자 순서 찾기 서브루틴

The goal of the quantum subroutine of Shor's algorithm is, given coprime integers ${\displaystyle N}$ and ${\displaystyle 1<a<N}$, to find the order ${\displaystyle r}$ of ${\displaystyle a}$ modulo ${\displaystyle N}$, ${\displaystyle r}$ ≡ 1($mod$N) ${\displaystyle$a^{$r}\equiv 1{\$pmod$${N}}만큼 가장 작은 양의 정수입니다. 이를 위해 쇼어의 알고리즘은 두 개의 레지스터를 포함하는 양자 회로를 사용합니다. 두 번째 레지스터는 $n{\displaystyle }$ ${\displaystyle$ $n$$}$ 큐비트를$$ 사용하며, 여기서 $n{\displaystyle }$ ${\displaystyle$ n$}$은 $N{\displaystyle \le {\mathrm{}}^{}}$ ${\displaystyle n^{}}$ ${\$ 2$^{n}$이 되도록 가장 작은 정수입니다$.$ 첫 번째 레지스터의 크기는 회로가 얼마나 정확한 근사치를 산출하는지를 결정합니다. ${\displaystyle \mathrm{2n}}$+ ${\displaystyle 1}$ ${\displaystyle 2n+1}$ 큐비트를$$ 사용하면 $r{\displaystyle }$ ${\displaystyle$ r$}$을(를) 찾을 수 있습니다$.$ 정확한 양자 회로는 문제를 정의하는 매개 변수 $a{\displaystyle }$ ${\displaystyle a}$ 및 $N$ ${\displaystyle$ N$}$에 따라 달라집니다$.$ 알고리즘에 대한 다음 설명은 $브라-켓$ 표기법을 사용하여 양자 상태를 나타내고 ⊗ {\$displaystyle$\otimes}는 논리적 OR 또는 논리적 XOR이 아닌 텐서 곱을 나타냅니다.

알고리즘은 크게 두 단계로 구성됩니다.

1. 양자 위상 추정은 {\$displaystyle a}$를$$곱하는 동작을 나타내는$$ $유니터리{\displaystyle }$ U ${\displaystyle U}$와 함께 사용합니다($$$모듈$ N ${\displaystyle$ N$}).$ $입력$ 상태 ${\displaystyle 0^{}}$⟩ ⊗ ${\displaystyle 2^{}}$ n +$1$⊗$$1 ⟩ {\displaystyle 0\rangle ^{\otimes$$2n+1}\otimes 1\rangle }(여기서 두 번째 레지스터는 n {\displaystyle n} 큐비트로 만든 ⟩ {\displaystyle 1\rangle })입니다. 이 $U$ ${\displaystyle$ U$}$의 고유값은 기간에 대한 정보를 인코딩하며, $1$⟩ ${\displaystyle$ 1\rangle }은 고유 벡터의 합으로 쓰기 가능한 것으로 볼 수 있습니다. 이러한 특성 덕분에 양자 위상 추정 단계는 ${\displaystyle {랜덤}^{}}$ $j$${\displaystyle {}^{}}$= ${\displaystyle 0,}$1$,$ r - 1 {\$displaystyle {\frac {j}{r}}2^{2n+1}$ $형태$의 ${\displaystyle {\mathrm{랜덤}}^{}}$ 정수를 출력으로 제공합니다.
2. 연속 분수 알고리즘을 사용하여 이전 단계에서 얻은 측정 결과에서$$ $주기{\displaystyle }$ r ${\displaystyle$ r$}$을 추출합니다. 이것은 출력 양자 상태를 측정하여 얻은 측정 데이터를 (클래식 컴퓨터로) 후처리하고 기간을 검색하는 절차입니다.

양자 위상 추정과의 연관성은 쇼어 알고리즘의 원래 공식에서는 논의되지 않았지만,^[2] 후에 Kitaev에 의해 제안되었습니다.^[22]

양자위상추정

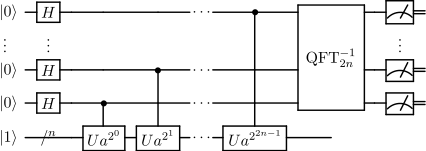
일반적으로 양자 위상 추정 알고리즘은 U$$ψ ⟩ = e 2 π i θ ψ ⟩ {\$displaystyle$ $}$ 및 고유 상태 ψ ⟩ {\$displaystyle$${\displaystyle }$\rangle}에 대해 U psi = e^{2\pi i\theta} \psi \rangle }, sends inputs states ${\displaystyle 0\rangle \psi \rangle }$ into output states close to ${\displaystyle \phi \rangle \psi \rangle }$, where ${\displaystyle \phi }$ is an integer close to ${\displaystyle 2^{2n+1}\theta }$. In other words, U$${\displaystyle U}의 각 고유 상태$$ψ j ⟩${\displaystyle$ \psi _${$$}\rangle$}을(를) 연관된 고유 값에 가까운 상태로 보냅니다. 양자 순서 찾기를 위해, 우리는 행동에 의해 정의된 유니터리를 사용하여 이 전략을 사용합니다.

≤ < 2 $n$k<2^{n}인 $상태$ ${\displaystyle k}$ ⟩ ${\displaystyle$ k\}에서 $U$ ${\displaystyle$ U$}$의 동작은 알고리즘의 기능에 중요하지 않지만 전체 변환이 잘 정의된 양자 게이트임을 보장하기 위해 포함되어야 합니다. $U{\displaystyle }$ ${\displaystyle U}$로 양자 위상 추정을 위한 회로를 구현하려면 게이트 U ${\displaystyle {{2j}^{}}^{}}$ ${\$ U$^{2^{j}}$를 효율적으로 구현할 수 있어야$$ 합니다$.$ 이는 알고리즘의 가장 느린 부분인 모듈식 지수화를 통해 달성할 수 있습니다. 이렇게 정의된 게이트는 ${\displaystyle Ur}$ = I ${\$displaystyle U$^{r$}= I}를 만족하며, 이는 고유값이 r {\displaystyle r}번째 일치 ω r k = e 2 π ik / r {\displaystyle \omega_{r}^{k}= e^{2\piik/r}}임을 즉시 의미합니다. 또한, 각 고유값$$ω r ${\displaystyle \omega_{$r}^{k}}는${}_{}$ψ j${}^{}$⟩ =$\underset{}{\overset{}{}}$r$$- $1$/ 2 ∑ k = 0 r - 1 ω r - k j k ⟩ {\textstyle \ psi _{j}\rangle = r^{-1/2}\sum _{k=0}^{r-1}\omega _{r}^{-kj} a^{k}\rangle } $형태$의 고유 벡터를 가지며, 이러한 고유 벡터는 다음과 같습니다.

여기서 $\underset{}{\overset{}{마지막}}$ 항등식은$$∑ $\underset{}{\overset{}{\mathrm{j}}}$ = $0$r - $1$ ω r j k = 0 {\textstyle \sum _{j=0}^{r-1}\omega _{r}^{jk}=0}을 의미합니다.

${\displaystyle 입력}$ 상태 0${\displaystyle {}^{}}$⟩ ⊗ ${\displaystyle 2}$ n${\displaystyle {}_{}}$+$$1 ψ j ⟩ {\$displaystyle$ 0\rangle ^{\otimes 2n+1} \psi _{j}\rangle }에서 양자 위상 추정을 사용하면 각 ϕ j {\displaystyle \phi _{j}\rangle ⟩ ψ {\displaystyle \phi _{j}\rangle }가 중첩을 나타내는 출력 ϕ j ⟩가 발생합니다. 약 ${\displaystyle {\mathrm{22n}}^{}}$+ ${\displaystyle {}^{}}$/ ${\displaystyle r}$ ${\displaystyle$ 2$^{2n+1}j/r}$ 정수$$중 가장 정확한 측정은 ≥ 4 π 2 ≈ 0.$4053 {\textstyle$\geq {\$frac {4}{\$pi ^{2}}\approx 0.4053}의 측정값입니다(추가 큐비트를 사용하여 임의로 1에 가깝게 만들 수 있습니다). ${\displaystyle {\mathrm{따라서}}^{}}$ 입력 ${\displaystyle 0{}^{}}$⟩ ⊗ ${\displaystyle 2}$ n${\displaystyle }$+$11$ ⟩ {\$displaystyle 0\rangle ^{\otimes$ 2n$+$1} 1\rangle } 대신 사용하면 출력은${\displaystyle j}$ =${\displaystyle 0}$, $...,$ r - 1 {\displaystyle j = 0,...,r-1}과 $같은$ 상태의 중첩입니다. 즉, 이 입력을 사용하면 $U{\displaystyle }$ ${\displaystyle U}$의 고유 벡터의 중첩에 대해 양자 위상 추정을 실행하는 것과 같습니다$.$ 보다 구체적으로, 양자 위상 추정 회로는 변환을 구현합니다.

첫 번째 레지스터를 측정하면 각$$ϕ j ⟩${\displaystyle$\phi_{j}\rangle }을 찾을 수 있는 균형 확률 $1{\displaystyle /r}$ ${\displaystyle 1/r}$이 있으며, 각 레지스터는$$22n + $1j$ /r${\displaystyle$2^{2n+1}j/r${\displaystyle \}}$의 정수${\displaystyle {}^{}}$를 제공합니다. ${\displaystyle {\mathrm{이}}^{}}$를 ${\displaystyle {22n\mathrm{}}^{}}$+ 1 {\$displaystyle$ 2$^{2n+1}}$로 나누어$$ $j{\displaystyle }$/ ${\displaystyle r}$ ${\displaystyle j/r}$에 대한 십진 근사치를 얻을 수 있습니다$.$

기간 검색을 위한 계속 분수 알고리즘

그런 다음 연속 분수 알고리즘을 적용하여 $정수$ b ${\textstyle b}$와 c ${\textstyle$ c$}$를 찾습니다$.$ 여기서 $\frac{\mathrm{bc}}{}$ ${\$는 회로에서 측정된 근사치에 대해 최상의 분수 근사치를 제공합니다$$. $b$ < N ${\textstyle$ b$,$$c$$<N}$ 및 coprime$b$ {\$textstyle b}$ 및 c${\textstyle$ c$}$입니다$.$ 근사의 정확도를 결정하는$$${\displaystyle \mathrm{2n}}$ + 1 ${\displaystyle$ 2n$+1}$ 첫 번째 $레지스터$의 큐비트 수는 다음을 보장합니다.

ϕ$$j ⟩ {\textstyle \phi_{j}\rangle}의 중첩으로부터 가장 좋은 근사치가 주어졌을 때 (추가 비트를 사용하고 출력을 잘라냄으로써 임의로 가능하게 만들 수 있음) 측정되었습니다. $그러나$ b ${\textstyle b}$ $및$ c ${\textstyle c}$는 coprime이지만 $j$ ${\textstyle j}$ $및$ r ${\textstyle r}$은 coprime이 아닐$$ 수 있습니다. 이 때문에 $b$ ${\textstyle b}$ 및$$ $c$ ${\textstyle$ c$}$에서 j ${\textstyle$ j$}$ 및$$ $r$ ${\textstyle r}$에 있던 일부 요소가 손실되었을$$ 수 있습니다$.$ 이는 임의의 횟수로 양자 서브루틴을 다시 실행하여 분수 근사치 목록을 생성함으로써 해결할 수 있습니다.$여기$서 ${\textstyles}$은(는) 알고리즘이 실행된 횟수입니다. 회로가 $여러$개의 $가능$한 j {\$textstyle$ c_{k$}$를 측정했기 때문에 각 ck$${\$textstyle$ j$}$에서 다른 ${인자}_{}$를 제거할$$수 있습니다. $실제$r {\$textstyle$r} 값을$$ ${복구}_{}$하려면 각$$ck {\$textstyle$c_{$k}$의 최소 공배수를 취할 수 있습니다$.$최소 공배수는 원래 $정수$ a ${\textstyle a}$의 차수 ${\textstyle$ r$}$$$ 확률이 높습니다.

첫번째 레지스터의 크기 선택

위상 추정은 알고리즘의 정확도를 결정하기 위해 첫 번째 레지스터의 크기를 선택해야 하며, 쇼어 알고리즘의 양자 서브루틴의 경우, ${\displaystyle 2}$ ${\displaystyle n}$+ ${\displaystyle 1}$ ${\displaystyle 2n+1}$ 큐비트는 위상 추정에서 측정된 최적의 비트${\displaystyle \mathrm{열}}$($k^{}$$⟩$ ${\displaystyle$ k$\$$rangle$}${의미}^{}$)을 보장하기에 충분합니다$.$ $여기$서 k /$22$n + $1 {\$textstyle k/2^{2n+1}는 위상 추정에서 위상의 가장 정확한 근사치입니다.)은 실제 값을 허용합니다.${\displaystyle r}$ ${\displaystyle$ r$}$을(를) 복구해야$$ 합니다.

Shor의 알고리즘에서 측정하기 전의$$각 ϕ j ⟩ {\$displaystyle$\phi_{j}\rangle}은${\displaystyle }$약$$22n + $1j$ / r${\displaystyle$2^{2n+1}j/r}에 $해당$하는 정수의 중첩을 나타냅니다. Let ${\displaystyle k\rangle }$ represent the most optimal integer in ${\displaystyle \phi _{j}\rangle }$. The following theorem guarantees that the continued fractions algorithm will recover ${\displaystyle j/r}$ from ${\displaystyle k/2^{2{n}+1}}$:

^[3] $k{\displaystyle }$ ${\displaystyle$ k$}$가 위상 추정의 최적 비트열이므로 $k{\displaystyle }$/ ${\displaystyle {22}^{}}$ n${\displaystyle {}^{}}$+ 1 ${\$는 j${\displaystyle }$/ ${\displaystyle r}$ ${\displaystyle j/r}$에 2 ${\displaystyle n}$+ ${\displaystyle 1}$ ${\displaystyle 2n+1}$ 비트만큼$$ 정확합니다$$. 따라서,

이는 연속 분수 알고리즘이 j ${\displaystyle$ j$}$ $및{\displaystyle }$ r$$ ${\displaystyle r}($또는 최대 공약수를 제거한 상태에서)를 복구한다는 것을 의미합니다.

병목현상

쇼어 알고리즘의 런타임 병목 현상은 양자 모듈 지수화로 양자 푸리에 변환 및 고전적인 사전/사후 처리보다 훨씬 느립니다. 모듈식 지수화를 위한 회로를 구성하고 최적화하는 방법에는 여러 가지가 있습니다. 가장 간단하고 (현재) 가장 실용적인 접근 방식은 리플 캐리 가산기로 시작하여 가역적인 게이트를 가진 기존의 산술 회로를 모방하는 것입니다. 기저와 지수 계수를 알면 추가 최적화가 용이합니다.^[23][24] 가역 회로는 일반적으로 $n{\displaystyle {}^{}}$ ${\$ $n$$^{3}$ 게이트의 ${\displaystyle {순서}^{}}$로 $n{\displaystyle }$ ${\displaystyle$ n$}$ 큐비트에$$ 사용됩니다. 대체 기술은 양자 푸리에 변환을 사용하여 게이트 수를 점근적으로 개선하지만 높은 상수로 인해 600 큐비트 미만으로 경쟁력이 없습니다.

기간 찾기 및 이산 로그

불연속 로그에 대한 Shor의 알고리즘과 순서 찾기 문제는 알고리즘이 주기 찾기 문제를 해결하는 예입니다.^{[citation needed]} 세 가지 모두 숨겨진 부분군 문제의 예입니다.

이산 로그에 대한 Shor의 알고리즘

Given a group ${\displaystyle G}$ with order ${\displaystyle p}$ and generator ${\displaystyle g\in G}$, suppose we know that ${\displaystyle x=g^{r}\in G}$, for some ${\displaystyle r\in \mathbb {Z} _{p}}$, and we wish to compute ${\displaystyle r}$, 이산 로그인 $r$ = ${\displaystyle {\log }_{}}$g ( x ) {\$display r$ = {\log _{g}(x)}입니다. 각 인자가 모듈식 값의 덧셈에 해당하는 아벨 군 Z p × Z p {\displaystyle \mathbb {Z}_{p}\times \mathbb {Z}_{p}를 생각해 보십시오. 이제, 함수를 생각해 보세요.

${\displaystyle f\colon \mathbb {Z} _{p}\times \mathbb {Z} _{p}\to G\;;\;f(a,b)=g^{a}x^{-b}}$

이는 아벨리안 은닉 부분군 문제를 제공하며, 여기서 $f{\displaystyle }$ ${\displaystyle$ f$}$는 군 동형에 해당합니다$$. 커널은${\displaystyle }$(${\displaystyle r,}$ ${\displaystyle 1)}$ ${\displaystyle (r, 1)}$의 배수에 해당합니다$.$ 따라서 커널을 찾을 수 있다면 r ${\displaystyle r}$을 찾을 수 있습니다$.$ 이 문제를 해결하기 위한 양자 알고리즘이 존재합니다. 이 알고리즘은 인자 찾기 알고리즘과 마찬가지로 Hadamard 게이트를 사용하여 중첩을 생성한 후$f{\displaystyle }$ {\$displaystyle$ f$}$를 양자 변환으로$$ 구현하고 마지막으로 양자 푸리에 변환으로 구현하기 때문입니다.^[3] 이 때문에 이산 로그를 계산하는 양자 알고리즘을 '쇼어의 알고리즘'이라고 부르기도 합니다.

순서 찾기 문제는 숨겨진 부분군 문제로도 볼 수 있습니다.^[3] 이를 보려면 아래 정수의 군과 $주어진$∈ $Z$ ${\$$display$ a$\in \mathbb$ {Z}에 $대하여$ ${\displaystyle 다음}$과 같은 r = 1 ${\displaystyle$ a^{r}=1}, 함수를 생각해 보십시오.

${\displaystyle f\colon \mathbb {Z} \to \mathbb {Z} \;;\;f(x)=a^{x},\;f(x+r)=f(x).}$

임의의 유한 아벨 군 $G{\displaystyle }$ ${\displaystyle G}$에 대하여$,$ $G{\displaystyle }$ ${\displaystyle G}$에 대한 숨겨진 부분군을 다항 시간에 풀기$$ 위한 양자 알고리즘이 존재합니다.^[3]

참고 항목

• GEECM, 인수분해 알고리즘 "종종 쇼어보다 훨씬 빠르다"^[25]
• 그로버 알고리즘

참고문헌

더보기

• Nielsen, Michael A. & Chuang, Isaac L. (2010), Quantum Computation and Quantum Information, 10th Anniversary Edition, Cambridge University Press, ISBN 9781107002173.
• Phillip Kaye, Raymond Laflamme, Michele Mosca, 양자 컴퓨팅 소개, Oxford University Press, 2007, ISBN 0-19-857049-X
• 스콧 애런슨(Scott Aaronson)의 "거리에 있는 사람을 위한 설명", 피터 쇼어(Peter Shor)의 "승인". (Shor)는 "훌륭한 기사예요, 스콧! 그것이 바로 제가 본 거리의 사람에게 양자 컴퓨팅을 설명하는 최고의 작업입니다.") QFT에 대한 대체 비유가 댓글 중 하나에서 제시되었습니다. 스콧 애런슨(Scott Aaronson)은 다음의 12개의 참고 문헌을 추가 판독으로 제안합니다("이미 웹에 있는¹⁰⁵⁰⁰⁰ 10개의 양자 알고리즘 튜토리얼" 중).
• Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM J. Comput., 26 (5): 1484–1509, arXiv:quant-ph/9508027v2, Bibcode:1999SIAMR..41..303S, doi:10.1137/S0036144598347011Peter Shor의 논문 원본 Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM J. Comput., 26 (5): 1484–1509, arXiv:quant-ph/9508027v2, Bibcode:1999SIAMR..41..303S, doi:10.1137/S0036144598347011수정본 ("28쪽, LaTeX). 이것은 1994년 11월 20일-22일, NM, Santa Fe, 컴퓨터 과학의 기초에 관한 제35회 연례 심포지엄(Proceedings on the Foundations of Computer Science, NM)에 등장한 논문의 확장판입니다. 1996년 1월("1996년 1월)의 사소한 개정.
• 양자 컴퓨팅과 쇼어의 알고리즘, Matthew Hayward의 양자 알고리즘 페이지, 2005-02-17, imsa.edu , LaTeX2원본 LaTeX 문서의 HTML 버전, PDF 또는 포스트스크립트 문서로도 사용 가능합니다.
• 양자 계산과 쇼어의 인수분해 알고리즘, Ronald de Wolf, CWI and University of 암스테르담, 1999년 1월 12일 9페이지 포스트스크립트 문서
• 2004년 10월 4일자 7페이지 포스트스크립트 문서, Berkeley CS 294-2 강의 9의 노트, Shor's Factoring Algorithm.
• 제6장 웨이백 머신에서 보관된 양자 계산 2020-04-30, 91페이지 포스트스크립트 문서, Caltech, Preskill, PH229.
• 양자 계산: Samuel L. Braunstein의 튜토리얼.
• 닐 영의 쇼어 알고리즘의 양자 상태 마지막 수정: 화 5월 211:47:38 1996.
• III. 양자 컴퓨터로 RSA 암호화 깨기: Shor's Factoring Algorithm, Connell University, Physics 481–681, CS 483; N. David Mermin의 2006년 봄. 최종 개정 2006-03-28, 30페이지 PDF 문서
• Lavor, C.; Manssur, L. R. U.; Portugal, R. (2003). "Shor's Algorithm for Factoring Large Integers". arXiv:quant-ph/0303175.
• Lomonaco, Jr (2000). "Shor's Quantum Factoring Algorithm". arXiv:quant-ph/0010034. 이 논문은 피터 쇼어의 양자 인수분해 알고리즘을 다룬 1시간짜리 강의의 서면 버전입니다. 22페이지입니다.
• 20장 양자 계산, 계산 복잡도로부터: 현대적 접근, 책의 초안: 2007년 1월 날짜, 프린스턴 대학의 산지브 아로라와 보아즈 바라크. 산지프 아로라의 양자계산 제10장 Boaz Barak, "계산 복잡도: 현대적 접근", Cambridge University Press, 2009, ISBN 978-0-521-426-4
• 양자 컴퓨팅을 향한 한 걸음: Wayback Machine에서 보관된 2011-01-20, "Discover Magazine", 2011년 1월 19일자.
• Josef Gruska - 양자 컴퓨팅에 대한 도전 또한 수학 무제한: 2001년 이상, 편집자 Björn Engquist, Wilfried Schmid, Springer, 2001, ISBN 978-3-540-66913-5

외부 링크

• libquantum 버전 1.0.0: 시뮬레이션된 양자 컴퓨터 라이브러리와 함께 Shor의 알고리즘의 C 언어 구현을 포함하지만 실행 시간 복잡성을 개선하려면 shor.c의 너비 변수를 1로 설정해야 합니다.
• PBS 인피니트 시리즈는 쇼어의 알고리즘 뒤에 숨겨진 수학을 설명하는 두 개의 영상인 '암호를 깨는 방법'과 '쇼어의 알고리즘으로 양자 속도로 해킹하기'를 만들었습니다.