트라히텐베르크 제도
Trachtenberg system트라히텐베르크 제도는 빠른 정신적 계산의 체계다.이 시스템은 산술 연산을 매우 빨리 수행할 수 있도록 쉽게 기억되는 연산으로 구성된다.나치의 강제수용소에 있는 동안 러시아 기술자 야코우 트라크텐베르그가 정신을 집중시키기 위해 개발한 것이다.
이 글의 나머지 부분은 트라히텐베르그가 고안한 몇 가지 방법을 제시한다.트라크텐베르그가 개발한 알고리즘 중 일부는 일반적인 곱셈, 나눗셈, 덧셈을 위한 알고리즘이다.또한 트라히텐베르크 시스템은 5에서 13 사이의 작은 숫자에 곱하기 위한 몇 가지 전문화된 방법을 포함한다(그러나 여기에 2-12가 표시됨).
추가 섹션은 곱셈에도 적용할 수 있는 계산을 확인하는 효과적인 방법을 보여준다.
일반 곱셈, 트라크텐베르크 수학 이론
일반 곱셈 방법은 공간 복잡성이 낮은 을(를) 곱하기 위한 방법이다. 즉, 메모리에 보관할 수 있는 임시 결과가 거의 없다.이는 최종 자릿수가 승수의 마지막 자릿수에 곱하여 완전히 결정된다는 점에 유의함으로써 달성된다.이것은 일시적인 결과로서 보류된다.다음 숫자를 찾으려면 이 숫자에 영향을 미치는 모든 것이 필요하다. 결과, 의 마지막 자릿수는 의 다음부터 마지막 자릿수인 b 의 다음부터 마지막 자릿수는 b 이다이 계산은 수행되며, 최종 두 자리수에서 정확한 임시 결과가 나온다.
일반적으로 최종 결과의 각 위치 에 대해 모든 을(를) 합한다
사람들은 이 알고리즘을 배울 수 있고 따라서 머릿속에 네 자리 숫자를 곱할 수 있다 – 최종 결과만을 적는다.그들은 가장 오른쪽 숫자로 시작해서 가장 왼쪽 숫자로 끝마칠 것이다.
트라히텐베르그는 이 알고리즘을 두 자릿수에 한 자릿수를 곱하는 쌍방향 곱셈의 일종으로 정의했는데, 기본적으로 결과의 중간 자릿수만을 유지한다.위의 알고리즘을 이 쌍의 곱셈으로 수행함으로써, 더 적은 수의 임시 결과를 보유할 필요가 있다.
예:
답의 첫 번째(가장 오른쪽) 숫자를 찾으려면 승수의 첫 번째 숫자에서 시작하십시오.
- 단위 자릿수 × . 6\
- 의 첫 번째 숫자는 10자리 은(는) 무시된다.
답의 두 번째 숫자를 찾으려면 승수의 두 번째 숫자에서 시작하십시오.
- 단위 자릿수는 에 수십 자릿수는 더하기
- 단위 자릿수 6
- + + = .
- 답의 두 번째 자릿수는 이며, 세 번째 자리까지 을(를) 운반한다.
답의 세 번째 숫자를 찾으려면 승수의 세 번째 숫자에서 시작하십시오.
- 단위 자릿수는 에 수십 자릿수는 5 더하기
- 단위 자릿수는 × 에 수십 자릿수는
- 자릿수 7
- 답의 세 번째 는 7이고, 자릿수로 1 을(를) 운반한다.
답의 네 번째 숫자를 찾으려면 승수의 네 번째 숫자에서 시작하십시오.
- 단위 자릿수 3 3 + 10 자리 수 +
- 단위 자릿수는 에 수십 자릿수는 더하기
- 단위 자릿수는 7\이고, 10 자릿수는 이다
- + + + + + 5+ = +5
- 답의 네 번째 자리는 6이고, 다음 자리까지 을(를) 운반한다.
동일한 방법으로 계속하여 나머지 숫자를 얻으십시오.
트라히텐베르크는 이것을 '2 핑거 메서드'라고 불렀다.위의 예에서 네 번째 숫자를 찾기 위한 계산은 오른쪽에 예시되어 있다.9의 화살표는 항상 승수의 숫자를 가리키며 찾으려는 답의 숫자 바로 위에 다른 화살표는 각각 한 자릿수를 오른쪽으로 가리킨다.각 화살표 헤드는 UT Pair 또는 Product Pair를 가리킨다.수직 화살표는 유닛 자릿수를 얻을 제품을 가리키고, 경사진 화살표는 제품 쌍의 십진수를 얻을 제품을 가리킨다.화살표가 숫자가 없는 공백을 가리킬 경우 해당 화살표는 계산되지 않는다.각 자릿수에 대해 해결할 때 모든 화살표가 접두사 0을 가리킬 때까지 각 화살표를 승수 위로 한 자리씩 왼쪽으로 이동시킨다.
트라히텐베르크 시스템의 분할은 곱셈에서와 거의 같지만 덧셈 대신 뺄셈으로 이루어진다.배당금을 더 작은 부분 배당금으로 나눈 다음, 이 부분 배당금을 디비저의 가장 왼쪽 자리 숫자로만 나누면 한 번에 한 자리씩 답이 나온다.답의 각 숫자를 풀면 부분 배당금에서 제품 쌍(UT 쌍)과 NT 쌍(숫자-텐)을 빼서 다음 부분 배당금을 찾는다.Product Pairs는 지금까지 답의 숫자와 구분자 사이에서 발견된다.감산 결과 음수가 나오면 한 자리를 백업하고 그 숫자를 한 자리만큼 줄여야 한다.충분히 연습하면 이 방법은 머릿속에서 할 수 있다.
일반추가
첫 번째 작업을 반복하지 않고 숫자 열을 추가하고 결과를 정확하게 확인하는 방법.중간 합계는 두 자릿수 행의 형태로 생성된다.중간 결과의 합을 L자형 알고리즘으로 취함으로써 답을 얻는다.마지막 단계로서, 둘 다 옹호되는 점검 방법은 원래의 오류를 반복할 위험을 제거하고 오류가 동시에 발생하는 정확한 열을 식별한다.이것은 nine-remainder 방법과 같은 체크(또는 자릿수) 합계를 기초로 한다.
절차가 효과적이 되려면 각 단계에서 사용하는 다른 조작을 구별해야 하며 그렇지 않으면 간섭의 위험이 있다.
기타 곱셈 알고리즘
이러한 곱셈 알고리즘 중 하나를 수행할 때는 다음과 같은 "단계"를 적용해야 한다.
답은 한 번에 한 자리씩 최소 유의한 자리부터 시작하여 왼쪽으로 이동해야 한다.마지막 계산은 승수의 선행 0에 있다.
각각의 자리에는 이웃, 즉 오른쪽에 있는 자리가 있다.가장 오른쪽 숫자의 이웃은 후행 0이다.
'할브' 작전은 트라히텐베르크 시스템에 특별한 의미를 갖는다.이것은 "반쪽 자리, 반올림"을 의미하지만, 속도 때문에 트라크텐베르크 제도를 따르는 사람들은 이 반쪽짜리 과정을 즉각적으로 만들도록 권장된다.그래서 "7명 중 절반이 3명이고, 그래서 3명"이라고 생각하는 대신에 "7명, 3명"이라고 생각하는 것이 제안된다.이렇게 하면 계산이 상당히 빨라진다.이와 같은 방법으로 10 또는 9에서 숫자를 빼기 위한 표를 기억해야 한다.
그리고 규칙이 이웃의 절반 추가를 요구할 때마다 현재 숫자가 홀수일 경우 항상 5를 추가하십시오.이것은 다음 자릿수의 계산에서 0.5를 떨어뜨린 것을 보충한다.
2로 곱하기
규칙: 각 자릿수에 2를 곱하십시오(내장 포함).
예: 8624 x 2
왼쪽에서 오른쪽으로 작업:
- 8+8=16,
- 6+6=12 (1에 해당),
- 2+2=4
- 4+4=8;
- 8624 x 2 = 17248
예제:76892 x 2
왼쪽에서 오른쪽으로 작업:
- 7+7=14
- 6+6=12
- 8+8=16
- 9+9=18
- 2+2=4;
- 76892 x 2 =153784
3 곱하기
규칙:
- 10에서 가장 오른쪽에 있는 숫자를 빼라.
- 9에서 나머지 자릿수를 뺀다.
- 결과를 두 배로 늘리다.
- 오른쪽에 이웃의 반을 더하고 숫자가 홀수일 경우 5를 더한다.
- 선행 0의 경우 이웃의 절반에서 2를 뺀다.
예제: 492 × 3 = 1476
오른쪽에서 왼쪽으로 작업:
- (10 - 2) × 2 + 0의 절반 = 166을 쓰고, 1을 운반한다.
- (9 - 9) × 2 + 2의 절반 + 2 (1) + 5 (9는 홀수이므로) + 1 (운반) = 7. 7. 쓰시오.
- (9 - 4) × 2 + 9(4)의 절반 = 14.4번 쓰세요, 1번 나르세요.
- 4의 절반 - 2 + 1 (운반) = 1. 쓰시오.
4 곱하기
규칙:
- 10에서 가장 오른쪽에 있는 숫자를 뺀다.
- 9에서 나머지 자릿수를 뺀다.
- 숫자가 홀수인 경우 이웃의 반을 더하고 5를 더한다.
- 선행 0의 경우 이웃의 절반에서 1을 뺀다.
예: 346×4 = 1384
오른쪽에서 왼쪽으로 작업:
- (10 - 6) + 0의 절반 = 4. 4를 쓴다.
- (9 - 4) + 6의 절반(3) = 8. 8을 쓴다.
- (9 - 3) + 4(2)의 절반 + 5 (3은 홀수이므로) = 13.3번 써라, 1번 나르세요.
- 3의 절반 - 1 + 1 (운반) = 1. 쓰시오.
5로 곱하기
- 규칙: 이웃의 절반을 가져간 다음, 현재 숫자가 홀수인 경우 5를 추가한다.
예: 42×5=210
- 2의 이웃인 0의 절반은 0이다.
- 4명의 이웃의 절반은 1이다.
- 선두 0의 이웃의 절반은 2이다.
- 43×5 = 215
- 3의 이웃의 절반은 0이고, 3은 홀수이기 때문에 5는 5이다.
- 4명의 이웃의 절반은 1이다.
- 선두 0의 이웃의 절반은 2이다.
- 93×5=465
- 3의 이웃의 절반은 0이고, 3은 홀수이기 때문에 5는 5이다.
- 9의 이웃의 절반은 1이고, 9는 이상해서 5는 6이다.
- 선두 0의 이웃의 절반은 4이다.
6 곱하기
규칙:
- 각 숫자에 인접 네트워크의 절반을 추가하십시오.현재 자릿수가 홀수인 경우 5를 추가하십시오.
예: 357 × 6 = 2142
오른쪽에서 왼쪽으로 작업:
- 7은 이웃이 없고, 5를 더하면(7은 홀수이므로) = 12이다.2번 쓰세요, 1번 들고 가.
- 5 + 7(3)의 절반 + 5(시작 자리 5가 홀수이므로) + 1(점수) = 14.4번 쓰세요, 1번 나르세요.
- 3 + 5(2)의 절반 + 5 (3은 홀수이기 때문에) + 1 (1) = 11.1을 쓰고, 1을 운반한다.
- 0 + 3 (1)의 절반 + 1 (운반) = 2. 2를 쓴다.
7 곱하기
규칙:
- 각 자릿수를 두 배로 늘린다.
- 그 이웃의 반을 더하라.
- 기본 자릿수가 홀수일 경우 5를 추가하십시오.
예: 523 × 7 = 3,661
오른쪽에서 왼쪽으로 작업:
- 3×2 + 0 + 5 = 11, 1.
- 2×2 + 1 + 1 = 6.
- 5×2 + 1 + 5 = 16, 6.
- 0×2 + 2 + 1 = 3.
8 곱하기
규칙:
- 10에서 가장 오른쪽 자리를 빼라.
- 9에서 나머지 자릿수를 뺀다.
- 결과를 두 배로 늘리다.
- 이웃을 추가하십시오.
- 선행 0의 경우 인접 항목에서 2를 뺀다.
예: 456 × 8 = 3648
오른쪽에서 왼쪽으로 작업:
- (10 - 6) × 2 + 0 = 8. 8을 쓴다.
- (9 - 5) × 2 + 6 = 14, 쓰기 4, 운반 1.
- (9 - 4) × 2 + 5 + 1 (16) =6을 쓰고, 1을 운반한다.
- 4 - 2 + 1 (운반) = 3. 3을 쓰시오.
9로 곱하기
규칙:
- 10에서 가장 오른쪽에 있는 숫자를 뺀다.
- 9에서 나머지 자릿수를 뺀다.
- 합에 인접 항목 추가
- 선행 0의 경우 인접 항목에서 1을 뺀다.
규칙 9, 8, 4, 3의 경우 첫 번째 자리만 10에서 뺀다.그 후, 각각의 자릿수는 대신 9에서 뺄셈이다.
예: 2,130 × 9 = 19,170
오른쪽에서 왼쪽으로 작업:
- (10 − 0) + 0 = 10.0을 쓰고, 1을 운반한다.
- (9 - 3) + 0 + 1 (운반) = 7. 7을 쓴다.
- (9 − 1) + 3 = 11.1을 쓰고, 1을 운반한다.
- (9 - 2) + 1 + 1 (운반) = 9. 9. 쓰시오.
- 2 - 1 = 1. 1을 쓰세요.
11 곱하기
규칙:
- 숫자를 옆에 추가하십시오.("이웃"으로 말하면, 우리는 오른쪽의 숫자를 의미한다.)
예:
- (0 + 3) (3 + 4) (4 + 2) (2 + 5) (5 + 0)
- 3 7 6 7 5
설명하기 위해:
- 11=10+1
그러므로,
12 곱하기
규칙: 12를 곱하는 방법:
맨 오른쪽 숫자부터 시작하여 각 숫자를 두 번 추가하고 이웃을 추가한다. ("이웃"은 오른쪽 숫자다.)
대답이 한 자리 수보다 크면 여분의 자리(1 또는 2)를 다음 작업으로 옮기기만 하면 된다.남은 자릿수는 최종 결과의 한 자릿수다.
예:
0316과 0316에서 이웃을 결정한다.
- 6번 자리에는 오른쪽 이웃이 없다.
- 숫자 1은 이웃 6을 가지고 있다.
- 숫자 3은 이웃 1을 가지고 있다.
- 숫자 0(접두사 0)에 인접 3이 있음
출판물
- 루산 지아트디노프, 사지드 무사.초등학생의 알고리즘적 사고를 위한 도구로서의 신속한 정신 계산 시스템.유럽 연구원 25(7): 1105-1110, 2012 [1].
- 야코우 트라히텐베르크의 기초수학 속도계 A.커틀러(트랜슬레이터), R. 맥쉐인(트랜슬레이터)은 1960년 뉴욕 더블웨이와 컴퍼니, Inc. 가든 시티에 의해 출판되었다.[1]
이 책에는 위의 각 연산에 대한 구체적인 대수적 설명이 수록되어 있다.
이 기사에 실린 대부분의 정보는 원저에서 나온 것이다.
곱셈 등에 대한 알고리즘/운용은 대수적 설명에 관한 장에도 불구하고 책이 명시하지 않은 다른 보다 작은 방법으로 표현할 수 있다.[a]
대중문화에서
2017년 미국 영화 '인디멘티드'는 7살 때 트라히텐베르크 시스템을 이용해 머릿속으로 계산을 해 스승에게 깊은 인상을 주는 신동 이야기를 다룬다.[2]
기타 시스템
정신수학에는 그 밖에도 여러 가지 계산법이 있다.아래 목록은 비록 완전히 정신적인 것은 아닐지라도, 계산하는 몇 가지 다른 방법을 보여준다.
- 바라티 크리슈나 티르타의 저서 "베딕 수학"
- 정신적 주판 – 학생들이 손가락으로 주판을 조작하는 것에 익숙해짐에 따라, 그들은 일반적으로 머리에 주판을 시각화하여 계산을 하도록 요청 받는다.거의 모든 숙련된 주판 사용자들은 정신적으로 산수를 하는 데 능숙하다.[citation needed]
- 지산밥
소프트웨어
이 섹션의 외부 연결 사용은 위키피디아의 정책이나 지침을 따르지 않을 수 있다.(2016년 5월)(이를 과 시기 |
다음은 교육 도구로 사용할 수 있는 알려진 프로그램 및 출처
웹
아이폰
안드로이드
메모들
- ^ 이 모든 정보는 1960년에 출판되고 인쇄된 원본에서 나온 것이다.원서는 7장의 장으로 되어 있으며, 길이는 270페이지나 된다.장의 제목은 다음과 같다.각 장의 수많은 하위 카테고리는 나열되지 않는다.트라히텐베르크 기초수학 속도계
- 1장 표 또는 표 없음
- 제2장 직접법에 의한 빠른 곱하기
- 3장 속도 곱셈-"두 손가락" 방법
- 제4장 덧셈과 정답
- 5장 분장 – 속도와 정확도
- 6장 정사각형 및 정사각형
- 제7장 방법의 대수적 설명
- 고속 곱셈, 나누기, 덧셈, 뺄셈, 제곱근을 위한 혁신적인 새로운 방법."(1960)
- "계산기 없이 고속 곱셈, 나누기, 덧셈, 뺄셈, 제곱근에 가장 잘 팔리는 방법."(2009년 재인쇄)
- 곱셈은 곱셈표 없이 이루어진다.
- 「70초에 5132437201 곱하기 4522736502785를 곱할 수 있는가?」 「트랙텐베르크 기초수학 속도계(tractenberg speed system of the Basic mathics)를 사용하여 한 어린 소년이 성공하였다.
- 야코우 트라크텐베르크(그 설립자)는 히틀러의 독일을 제2차 세계대전이 끝날 무렵의 활동적인 기관에서 탈출했다.트라크텐베르크 교수는 자신의 조국 러시아에서 황제의 정권이 전복되자 독일로 도망쳐 30대 중반까지 그곳에서 평화롭게 살았다.그는 도망자였고 붙잡혔을 때, 총 7년을 다양한 강제 수용소에서 보냈다.트라히텐베르크 교수가 스피드 수학의 체계를 고안한 것은 이 몇 년 동안이었다.그의 작업은 대부분 펜이나 종이 없이 이루어졌다.그러므로 대부분의 기술은 정신적으로 수행될 수 있다.
참조
- ^ Trachtenberg, Jakow (1960). Cutler, Ann (ed.). The Trachtenberg Speed System of Basic Mathematics]. Translated by A. Cutler, R. McShane. Doubleday and Company, Inc. p. 270. 1962년판:ISBN9780285629165.
- ^ @GiftedtheMovie (9 March 2017). "Hobbies include playing with legos and learning the Trachtenberg system 👷♀️📚✏️ @McKennaGraceful is Mary // #GiftedMovie" (Tweet) – via Twitter.
추가 읽기
- 트라히텐베르크, J. (1960).트라히텐베르크 기초수학 속도계미국 뉴욕 가든 시티의 더블데이 앤 컴퍼니.
- Катлер Э., Мак-Шейн Р.ссеаааооо п п п п паааааааааа п п паееа,, 1967년(러시아어)
- 루산 지아트디노프, 사지드 무사."초등학생의 알고리즘적 사고를 위한 도구로서의 신속한 정신 계산 시스템," 유럽 연구원 25(7): 1105-1110, 2012.
외부 링크
- 찬드라셰카르, 키란웨이백 머신에서 "[Learn All about] Mathematical 바로 가기", SapnaEdu.in(2018년 5월 30일 방영)
- 영재(2017년 영화) 이 영화는 트라히텐베르크 제도에 대한 내용으로, 이 기법을 배운 젊은 예술가 매키나 그레이스가 주인공을 맡았다.

 마지막 자릿수는
마지막 자릿수는 






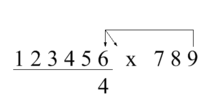
 수십 자릿수는
수십 자릿수는 


 , 세 번째 자리까지
, 세 번째 자리까지

 수십 자릿수는
수십 자릿수는 

 ,
, 

 수십 자릿수는
수십 자릿수는  , 10 자릿수는
, 10 자릿수는 









![{\begin{aligned}6\times 2&=12{\text{ (2 carry 1) }}\\1\times 2+6+1&=9\\3\times 2+1&=7\\0\times 2+3&=3\\0\times 2+0&=0\\[10pt]316\times 12&=3,792\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/943f833e78415c7525b0e939b2d7c2a17d627f3a)


