파괴 역학

균열 팁의 하중은 세 가지 독립적인 응력 강도 계수의 조합으로 감소될 수 있습니다.

파괴 역학은 재료의 균열 전파에 관한 연구와 관련된 역학 분야입니다.분석 고체 역학 방법을 사용하여 균열의 구동력을 계산하고 실험 고체 역학 방법을 사용하여 재료의 파괴 저항성을 특징짓습니다.

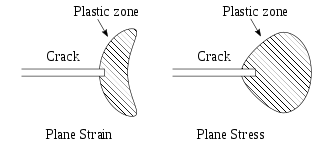
이론적으로 날카로운 균열 선단 앞의 응력은 무한하므로 균열 주변의 상태를 설명할 수 없다.균열 역학은 균열의 하중을 특징짓기 위해 사용되며, 일반적으로 균열 끝의 전체 하중 상태를 설명하기 위해 단일 매개변수를 사용합니다.다양한 파라미터가 개발되었습니다.균열 끝의 플라스틱 부위가 균열 길이에 비해 작은 경우 균열 끝의 응력 상태는 재료 내부의 탄성력에 의한 것으로 LEFM(Linear Elastic Fracture)이라 불리며 응력 강도 $계수$ K(\ $displaystyle$ K $K$ 를 이용하여 특징지을 수 있다.제멋대로, 1957년 G. Irwin은 어떠한 상태라도 세 가지 독립적인 스트레스 강도 인자의 조합으로 감소될 수 있음을 발견했다.

Mode I – 개방 모드(균열 면에 수직인 인장 응력),
Mode II – 슬라이딩 모드(균열 면과 평행하고 균열 전면에 수직인 전단 응력) 및
모드 III – 찢김 모드(균열면과 평행하고 균열전면에 평행하게 작용하는 전단응력)

균열 팁의 플라스틱 부위가 너무 크면 J 적분이나 균열 팁 개구부 변위 등의 파라미터와 함께 탄성 플라스틱 파단 역학을 사용할 수 있다.

특성화 매개변수는 균열 팁의 상태를 나타내며, 균열 팁은 유사성을 보장하기 위해 실험 조건과 관련될 수 있습니다.균열 성장은 파라미터가 일반적으로 특정 임계값을 초과할 때 발생합니다.응력 부식 응력 강도 임계값을 초과하면 균열이 서서히 커질 수 있다.마찬가지로 작은 결함도 반복 하중을 가할 때 균열이 커질 수 있다.피로( fatigue cracks)로 알려진 긴 균열의 경우 성장률은 하중을 가하여 균열에서 발생하는 응력강도 $\Delta K$ K(\ $displaystyle\Delta$ K $)$ 의 $\Delta K$ 범위에 따라 크게 좌우되는 것으로 나타났다.응력 강도가 재료의 파단 인성을 초과하면 빠른 파단이 발생합니다.균열 성장 예측은 내손상성 기계 설계 분야의 핵심이다.

동기

재료 제조, 가공, 가공 및 성형 공정은 완성된 기계 부품에 결함을 초래할 수 있습니다.제조 공정에서 발생하는 내부 및 표면 결함은 모든 금속 구조에서 발견됩니다.이러한 모든 결함이 서비스 조건 하에서 불안정한 것은 아닙니다.파괴 역학은 안전한(즉, 성장하지 않는) 결함 및 균열로 전파되기 쉬운 결함 및 결함 구조의 고장을 일으키는 결함을 발견하기 위한 분석입니다.이러한 본질적인 결함에도 불구하고, 손상 내성 분석을 통해 구조물의 안전한 작동을 달성할 수 있다.골절 역학은 중요한 연구의 대상으로서 100년 동안 거의 존재하지 않았기 때문에 비교적 ^[1]^[2]새로운 것이다.

파괴 역학은 다음과 ^[2]같은 질문에 대한 정량적 답변을 제공해야 한다.

균열크기의 함수로 구성부품의 강도는 얼마입니까?
서비스 하중을 받을 때 허용되는 균열 크기는 어느 정도입니까? 즉, 최대 허용 균열 크기는 얼마입니까?
균열이 초기 크기(예: 최소 탐지 가능한 균열 크기)에서 최대 허용 가능한 균열 크기까지 커지는 데 얼마나 걸립니까?
특정 기존 결함 크기(예: 제조 결함)가 존재한다고 가정할 때 구조물의 수명은 얼마나 됩니까?
균열검출 가능한 기간 동안 구조물의 균열 여부를 얼마나 자주 점검해야 하는가?

선형탄성파괴역학

그리피스 기준

길이(\displaystyle

a

)

의

a

그리피스 균열(날개)이 중앙에^[3]^[4] 무한대의 큰 재료입니다.

파단 역학은 1차 세계대전 중에 영국 항공 기술자 A에 의해 개발되었다. A. 그리피스(즉 그리피스 균열)는 부서지기 쉬운 ^[5]물질의 고장을 설명하기 위한 것입니다.그리피스의 연구는 두 가지 모순된 사실에 의해 동기를 부여받았다.

벌크 글라스를 깨는 데 필요한 응력은 약 100MPa(15,000psi)입니다.
유리의 원자 결합을 깨는 데 필요한 이론적 응력은 약 10,000 MPa(1,500,000 psi)입니다.

이러한 상반된 관찰을 조화시키기 위해 이론이 필요했다.또 그리피스가 직접 실시한 유리섬유 실험 결과 섬유지름이 작아질수록 파괴응력이 증가하는 것으로 나타났다.따라서 그리피스 이전에 재료 고장을 예측하기 위해 광범위하게 사용되었던 단축 인장 강도는 표본에 의존하지 않는 재료 특성이 될 수 없었다.그리피스는 낮은 골절 강도 실험에서 관찰되지만 뿐만 아니라 힘의 size-dependence와, 아주 작은 결함의 대량 물질의 존재 때문에 있다고 시사했다.

이러한 결함 가설을 확인하기 위하여, 그리피스는 실험적인 유리 표본에 인공 결함을 소개했다.인공 결함 많은 표본에 다른 결함 더 크다는 표면 균열의 형태에 있었다.그 실험들은 결함 길이(한{\displaystyle})의 제곱 근과 골절(σ f{\displaystyle \sigma_{f}})에서 스트레스 제품 거의, 방정식으로 표현되어 변하지 않는 것이었고: 보여 주었다.

\sigma _{f}{\sqrt {a}}\about C

선형 탄성 이론의 관점에서 이 관계를 설명하는 것은 문제가 있다.선형 탄성 이론은 선형 탄성 재료의 날카로운 흠집 끝에 있는 응력(그러므로 변형률)이 무한하다고 예측합니다.그 문제를 피하기 위해 그리피스는 그가 관찰한 관계를 설명하기 위해 열역학적인 접근법을 개발했다.

균열의 성장, 즉 균열의 양쪽에 있는 표면의 연장은 표면 에너지의 증가를 필요로 한다.Griffith는 탄성판의 유한 균열의 탄성 문제를 해결하여 균열의 표면 에너지 측면에서 $상수$ C {\ $displaystyle$ C $}$ 에 $C$ 대한 식을 구하였다.간단히 말하면, 접근법은 다음과 같습니다.

단축 인장하중을 받는 상태에서 완벽한 시료에 저장된 전위에너지를 계산한다.
가해진 하중이 작용하지 않도록 경계를 고정하고 시료에 균열을 도입한다.균열은 응력을 완화시켜 균열면 근처의 탄성 에너지를 감소시킨다.한편, 균열은 시료의 총 표면 에너지를 증가시킨다.
자유에너지(표면에너지 - 탄성에너지)의 변화를 균열길이의 함수로 계산한다.자유에너지가 임계 균열길이의 피크값에 도달했을 때 고장이 발생하며, 이 값을 초과하면 균열길이의 증가에 따라 자유에너지가 감소한다(즉, 파단을 일으킴).이 절차를 통해 그리피스는

C=sqrt {\pi }} {\pi }

$E$ 서 E $(\displaystyle$ E $)$ 는 $E$ 재료의 영 계수이고 $\gamma$ (\ $displaystyle \gamma)$ 는 $\gamma$ 재료의 표면 에너지 밀도입니다.E $E=62\ {\text{GPa}}$ $E=62\ {\text{GPa}}$ $E=62\ {\text{GPa}}$ (\ $displaystyle$ E $=62\\text{)$ 라고 $E=62\ {\text{GPa}}$ 합니다. $GPa}}$ 및 $E=62\ {\text{GPa}}$ $\gamma =1\ {\text{J/m}}^{2}$ $\gamma =1\ {\text{J/m}}^{2}$ $\gamma =1\ {\text{J/m}}^{2}$ J/ $\gamma =1\ {\text{J/m}}^{2}$ {{ $displaystyle$ \ $displaystyle = 1\{text{J/m}}^2}}$ 은 $\gamma =1\ {\text{J/m}}^{2}$ Griffith의 예측파괴응력과 유리의 실험결과가 매우 일치한다.

하중과 수직인 균열이 있는 단순한 직사각형 판의 경우 에너지 방출 속도 G $(\display G$ 는 다음과 같습니다.

({displaystyle G=syslogfrac ^{2}a}{E}}

여기서 $\sigma$ δ { $displaystyle \sigma}$ 는 $\sigma$ $가해진$ 응력, { $displaystyle$ a $}$ 는 $a$ 균열 길이의 절반, $E$ {\ $displaystyle$ E $}$ 는 $E$ 영 계수입니다. 평면 변형률의 경우 이를 플레이트 $계수$ ( $(1-\nu ^{2})$ - $†$ 2)로 나누어야 합니다 $(1-\nu ^{2})$ 변형률 에너지 방출 속도는 물리적으로 균열의 성장에 의해 에너지가 흡수되는 속도로 이해할 수 있습니다.

단, 다음과 같은 것도 있습니다.

({displaystyle G_{c}=blac {pi \f}^{2}a}{E}},

$G$ { $displaystyle$ G} $G_{c}$ c { $displaystyle$ G _ { $c$ } $G_{c}$ , $G$ ≥ ≥ 、 $G_{c}$ 전파를 시작하는 기준입니다.

균열 전파 전 변형률이 높은 재료의 경우 선형 탄성 파괴 역학 제형이 더 이상 적용되지 않으며, 연질 재료의 파단 등 균열 선단에 가까운 응력 및 변위장을 기술하기 위해 적합한 모델이 필요하다.

어윈의 수정

연성재료의 균열선단부 주변의 소성부

그리피스의 작업은 1950년대 초반까지 공학계에 의해 대부분 무시되었다.그 이유는 (a) 실제 구조 재료에서 파괴를 일으키는 데 필요한 에너지 수준이 해당 표면 에너지보다 크기이고, (b) 구조 재료에서는 균열 전면 주위에 항상 다음과 같은 선형 탄성 매체의 가정을 만드는 몇 가지 비탄성 변형이 있기 때문이다.균열 끝의 무한 응력이 매우 비현실적입니다. ^[6]

그리피스의 이론은 유리와 같은 부서지기 쉬운 재료에 대한 실험 데이터와 매우 일치합니다.강철과 같은 연성 재료는 $\sigma _{f}{\sqrt {a}}=C$ f $\sigma _{f}{\sqrt {a}}=C$ $=$ {\ $displaystyle \displaystyle$ _ ${f}{\displayrt {a$ }}= $C}$ 의 $\sigma _{f}{\sqrt {a}}=C$ 관계는 유지되지만 그리피스 이론에 의해 예측되는 표면 에너지(displaystyle \displayrt {a}=C})는 일반적으로 비현실적으로 높다.제2차 세계대전 중 미국 해군 연구소의 G. R. 어윈^[7] 밑에서 일하는 한 그룹은 가소성이 연성 물질의 파괴에 중요한 역할을 해야 한다는 것을 깨달았다.

연성 재료(그리고 부서지기 쉬운 것으로^[8] 보이는 재료에서도)에서는 균열의 끝에 플라스틱 영역이 형성됩니다.가해지는 하중이 증가함에 따라 균열의 크기가 커지고 균열 끝의 탄성 변형 물질이 배출될 때까지 플라스틱 구역의 크기가 커진다.균열 팁 근처의 플라스틱 로딩 및 언로드 사이클은 열로 인한 에너지 소산으로 이어집니다.따라서 그리피스가 메짐성 물질에 대해 고안한 에너지 균형 관계에 소멸 용어를 추가해야 합니다.물리적 측면에서 연성 재료의 균열 성장에 있어 메짐성 재료에 비해 추가적인 에너지가 필요하다.

Irwin의 전략은 에너지를 두 부분으로 나누는 것이었습니다.

균열이 커짐에 따라 방출되는 축적된 탄성 변형 에너지.이것이 골절의 열역학적 추진력이다.
소성 소산과 표면 에너지(및 작용하고 있을 수 있는 기타 모든 소멸력)를 포함하는 소멸 에너지.소멸된 에너지는 열역학적 파괴 저항성을 제공합니다.그러면 총 에너지는

G=2\gamma +G_{p}

여기서 $\gamma$ { $displaystyle \gamma }$ 는 $\gamma$ 표면 $G_{p}$ 이며 G $G_{p}$ p { $displaystyle G_{p}$ 는 $G_{p}$ 균열 성장 단위 면적당 소성 소산(및 다른 소스로부터의 소산)입니다.

그리피스의 에너지 기준의 수정된 버전은 다음과 같이 기록될 수 있습니다.

\displaystyle _{f}{\displayrt {a}}=\displayrt {E~G}{\pi }}}.}

유리 등 연성 재료의 경우 표면 에너지 항이 $G\approx 2\gamma =2\,\,{\text{J/m}}^{2}$ 이며 G $G\approx 2\gamma =2\,\,{\text{J/m}}^{2}$ 2 $G\approx 2\gamma =2\,\,{\text{J/m}}^{2}$ 2 $G\approx 2\gamma =2\,\,{\text{J/m}}^{2}$ 2 {\ $display style$ G $\approx$ 2 $=$ 2 $,$ {\ $text {J/m}$ ^ $2$ {\ $G\approx G_{p}=1000\,\,{\text{J/m}}^{2}$ { $G\approx G_{p}=1000\,\,{\text{J/m}}^{2}$ /m} } {{2}} {\display G\ $style$ G p $G\approx G_{p}=1000\,\,{\text{J/m}}^{2}$ $G\approx G_{p}=1000\,\,{\text{J/m}}^{2}$ J/ $G\approx G_{p}=1000\,\,{\text{J/m}}^{2}$ 2 {\p } {\ $display$ G\style G\style G\style } {\display} {\display } {\disp} {\disp}} {\display}}유리 전이 온도에 가까운 폴리머의 $(\displaystyle$ G $)$ 값은 $G$ 2 ~ $(\$ {J/ $m}^2$ 입니다.

응력 강도 계수

Irwin과 그의 동료들이 이룬 또 다른 중요한 성과는 선형 탄성 ^[7]고체에서 균열 전면 주변의 점근 응력과 변위장의 관점에서 파괴에 사용할 수 있는 에너지의 양을 계산하는 방법을 찾는 것이었습니다.모드 I 로딩의 스트레스 필드에 대한 이 점근식은 다음과 ^[9]같은 스트레스 강도 계수_I K와 관련이 있습니다.

\displaystyle _{ij}=\left\displayac {K_{I}}{\sqrt {2\pi r}}\right}~f_{ij}(\theta)}

여기서 θ는_ij Cauchy 응력, r은 균열 팁으로부터의 거리, θ는 균열 평면에 대한 각도_ij, f는 균열 형상 및 하중 조건에 따라 달라지는 함수이다.어윈은 K 양을 스트레스 강도 인자라고 불렀다.f의 양이_ij 무차원적이므로 응력 강도 계수는 ${\text{MPa}}{\sqrt {\text{m}}}$ m \ $displaystyle$ \ text ${$ } $단위$ 로 표시할 수 있습니다. $MPa}}$ {\ $sqrt {text {m$

응력 강도가 변형률 에너지 방출 속도를 대체하고 파괴 인성이라는 용어가 표면 약점 에너지를 대체했습니다.이 두 용어는 그리피스가 사용한 에너지 항과 단순히 관련이 있습니다.

\displaystyle K_{I=\sigma {\pi a}

그리고.

K_{c}={\sqrt {EG_{c}}}\,

c

K_{c}={\sqrt {EG_{c}}}\,

K_{c}={\sqrt {EG_{c}}}\,

K_{c}={\sqrt {EG_{c}}}\,

{

displaystyle K_{c

} =

sqrt {EG_{c}},}

(평면 응력용)

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

c

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

1 -

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

2

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

{

displaystyle K_{c

} =

sqrt

{

frac

{

EG

_ { c } { 1 - \

nu

^ {2

}

} } （

K_{c}={\sqrt {\frac {EG_{c}}{1-\nu ^{2}}}}\,

strain strain ）

$K_{I}$ 서 $(\$ $I}$ 는 $K_I$ 응력 강도, $K_{c}$ c $K_{c}$ { $display style$ K _ { $c$ }는 $K_{c}$ 파괴 인성, $\nu$ {\ { \ $display$ style \ $nu }$ 는 $\nu$ Poisson의 비율입니다.

골절은 $K_{I}\geq K_{c}$ c $\$ 에서 $K_{I}\geq K_{c}$ 합니다. $I}\geq K_{c$ 평면 스트레인 변형의 특수한 경우 $K_{c}$ c { $style$ K_ ${c}$ 는 $K_c$ $K_{Ic}$ $K_{Ic}$ c { $style$ K_ ${Ic}$ 가 $K_{Ic}$ $K_{Ic}$ 재료 특성으로 간주됩니다.첨자 I은 균열이 확산될 수 있도록 재료를 적재하는 방법이 다르기 때문에 발생합니다.모드 II 또는 III가 아닌 이른바 "모드 I" 로딩입니다.

$K_{I}$ 의 $K_{I}$ (\ $style$ K_ ${$ $I}}$ 는 $K_I$ 응력강도계수에 관한 기사에서 설명한 바와 같이 중심 균열 무한판 이외의 기하학적 구조에서는 다르다.따라서 형상을 특징짓기 위해 무차원 보정 계수 Y를 도입할 필요가 있다.흔히 기하학적 형상 계수라고도 하는 이 보정 계수는 경험적으로 결정된 직렬에 의해 주어지며 균열 또는 노치의 유형과 형상을 설명합니다.다음과 같은 것이 있습니다.

\displaystyle K_{I)=Y\sigma(Y\sigma)

여기서 Y는 길이 2a의 관통 두께 균열을 포함하는 유한 폭 W의 시트에 대해 주어진 시트의 균열 길이와 폭의 함수이다.

\displaystyle Y\left({\frac {a}){W}}\오른쪽)= sqrt {\sec \ left \ frac \ pi a }W}}\right}}}}},

변형 에너지 방출

Irwin은 균열의 크기에 비해 균열 주변의 플라스틱 구역의 크기가 작을 경우 균열 ^[6]끝의 응력(플라스틱 구역) 상태에 따라 균열 성장에 필요한 에너지가 크게 좌우되지 않는다는 것을 최초로 관찰했다.즉, 순수 탄성 용액을 사용하여 파괴에 사용할 수 있는 에너지의 양을 계산할 수 있다.

균열성장에 대한 에너지 방출률 또는 변형률 방출률은 균열성장의 단위면적당 탄성 변형률의 변화로 계산할 수 있다.

\displaystyle G:=\left[{\cfrac U}{\partial a}}\right]_{P}=-\left[{\cfrac {\partial U}{\partial a}}\right]_{u}

여기서 U는 시스템의 탄성 에너지이고 a는 균열 길이입니다.상기 식을 평가하면서 부하 P 또는 변위 u 중 하나가 일정하다.

I 균열 모드(개방 모드)의 경우 스트레인 에너지 방출 속도와 응력 강도 계수는 다음과 같이 관련이 있음을 Irwin은 보여주었습니다.

G=G_{I}=snotbegin{case}{\cfrac {K_{I}^{2}}{E}}&{\text{평면응력}}\{\cfrac{(1-\nu^{2})K_{I}^{2}}{E}}&{\text {plane strain}}\end {case}

여기서 E는 영 계수, θ는 포아송 비율, K는_I 모드 I의 스트레스 강도 계수입니다.Irwin은 또한 선형 탄성체 내 평면 균열의 변형 에너지 방출 속도는 가장 일반적인 하중 조건에 대한 모드 I, 모드 II(슬라이딩 모드) 및 모드 III(티어링 모드) 응력 강도 인자로 표현될 수 있음을 보여주었다.

다음으로, Irwin은 메짐성 파괴 동안 에너지 소산 구역의 크기와 모양이 거의 일정하게 유지된다는 추가 가정을 채택했다.이 가정은 단위 파괴 표면을 생성하는 데 필요한 에너지가 재료에만 의존하는 상수임을 시사합니다.이 신소재 특성은 파단 인성(fracture strength)이라는 이름으로 지정되었고 G로 지정되었다_Ic.오늘날, 평면 변형 조건에서 발견되는 임계 응력 강도 계수_Ic K는 선형 탄성 파괴 역학의 정의 특성으로 받아들여진다.

균열 선단 플라스틱 구역

이론적으로 반지름이 거의 0에 가까운 균열 끝의 응력은 무한대인 경향이 있다.이는 응력 특이점으로 간주되며 실제 애플리케이션에서는 가능하지 않습니다.이러한 이유로 파괴 역학 분야의 수치 연구에서 균열 끝 특이점을 ^[9]대체하는 응력 집중의 기하학적 의존 영역을 사용하여 균열을 둥근 끝 노치로 표현하는 것이 종종 적절하다.실제 실제 재료 내 균열 끝의 응력 농도는 유한하지만 시료에 가해지는 공칭 응력보다 큰 것으로 밝혀졌다.

그럼에도 불구하고, 그러한 균열이 자발적으로 확산되는 것을 방지하는 어떤 종류의 메커니즘이나 특성이 있어야 한다.균열 팁의 소성 변형으로 균열 팁이 효과적으로 흐려지는 것으로 가정합니다.이러한 변형은 주로 적용 가능한 방향으로 가해지는 응력(대부분의 경우 이것은 일반 데카르트 좌표계의 y방향), 균열 길이 및 ^[10]시료의 형상에 따라 달라진다.이 소성 변형 구역이 균열 팁에서 어떻게 확장되었는지를 추정하기 위해 Irwin은 재료의 항복 강도를 균열을 따라 Y 방향의 원계 응력과 동일시하고 유효 반지름에 대해 해결했습니다.Irwin은 이 관계에서 균열의 하중이 임계응력강도계수에 가해진다고 가정하고 균열 끝의 소성변형부 이상반경에 대해 다음과 같은 식을 개발하였다.

({displaystyle r_{p}=black {K_{C}^2}}{2\pi \pi \pi _{Y}^2}}}

이상적인 재료 모델을 통해 이 가소성 구역이 균열 ^[11]끝의 중심에 있음을 알 수 있었습니다.이 방정식은 균열 팁 너머의 플라스틱 구역 변형의 대략적인 이상적인 반지름을 제시하는데, 이는 재료가 응력을 받았을 때 어떻게 반응하는지에 대한 좋은 추정치를 제공하기 때문에 많은 구조 과학자들에게 유용합니다.상기 식에서 응력강도계수 및 재료인성 $K_{C}$ 인 K C $(\$ 와 항복응력 $\sigma _{Y}$ Y(\ $displaystyle \sigma$ _ ${Y$ 의 파라미터는 재료와 재료의 특성 및 플라스틱 영역에 대한 많은 것을 나타내기 때문에 중요하다. $K_{c}$ 를 들어 $K_{c}$ c $K_{c}$ { $display$ $style$ K _ $K_{c}$ { $c$ } , 、 Y $\sigma _{Y}$ { $display$ style \ $\sigma _{Y}$ _ { $Y$ } , , , , $\sigma _{Y}$ ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile ile이 두 파라미터의 비율은 플라스틱 존의 반지름에 중요합니다.예를 들어 $\sigma _{Y}$ Y \ $display$ style \ $sigma$ _ { $Y$ } , $K_{C}$ \ $display$ $style$ K _ { $C$ } $\sigma _{Y}$ Y \ $sigma$ _ { $Y$ }의 $\sigma_Y$ $K_{C}$ $\sigma_Y$ 제곱비가 크므로 플라스틱 반경이 커집니다.이는 재료가 소성 변형될 수 있으므로 견고함을 의미합니다.^[10]균열 팁 너머의 플라스틱 구역의 크기를 추정하면 균열이 있을 때 물질이 어떻게 반응하는지를 보다 정확하게 분석할 수 있습니다.

단일 이벤트 로드에 대해 위에서 설명한 것과 동일한 프로세스가 및 주기적 로딩에도 적용됩니다.반복하중을 받는 시료에 균열이 있으면 균열 끝부분이 소성변형을 일으켜 균열성장을 지연시킨다.과부하 또는 이탈의 경우, 이 모델은 재료가 이전에 경험한 응력의 급격한 증가를 수용하기 위해 약간 변경됩니다.충분히 높은 하중(과부하)에서 균열은 그것을 포함하고 있던 플라스틱 영역에서 자라나 원래의 플라스틱 변형 주머니를 남긴다.이제 과부하 응력이 시료를 완전히 파괴할 정도로 높지 않다고 가정할 때, 균열은 새로운 균열 선단 주변에서 추가적인 소성 변형을 일으켜 잔류 소성 응력 영역을 확대한다.이 과정은 새로운 플라스틱 영역이 일반적인 스트레스 조건보다 크기 때문에 재료의 수명을 더욱 강화하고 연장합니다.이를 통해 재료는 더 많은 로드 사이클을 거치게 됩니다.이 아이디어는 알루미늄 그래프로 설명할 수 있으며 중심 ^[12]균열은 과부하 현상을 일으킵니다.

제한 사항

1943년 SS 스넥터디호는 입항 중 부서지기 쉬운 골절로 갈라졌다.

그러나 NRL 연구진에게 문제가 생긴 것은 선박용 철과 같은 해군 재료는 완벽한 탄성은 없지만 균열의 끝에서 상당한 소성 변형을 겪기 때문이다.Irwin의 선형 탄성 파단 역학의 기본 가정 중 하나는 균열 길이에 비해 플라스틱 구역의 크기가 작은 조건인 작은 항복이다.그러나 이러한 가정은 구조강의 특정 유형의 기능 상실에 대해서는 상당히 제한적이지만 이러한 강재는 다수의 치명적인 기능 상실을 초래하는 메짐성 파괴를 일으킬 수 있다.

선형 탄성 파괴 역학은 구조용 강철에 제한적으로 사용되므로 파괴 인성 시험은 비용이 많이 들 수 있습니다.

탄성-소성 파괴 역학

아메리칸 항공 587편과 분리된 수직 안정기가 치명적인 추락으로 이어졌다.

대부분의 엔지니어링 재료는 큰 ^{[citation needed]}하중을 수반하는 작동 조건 하에서 일부 비선형 탄성 및 비탄성 거동을 보여줍니다.이러한 재료에서 선형 탄성 파괴 역학의 가정은 유지되지 않을 수 있다. 즉,

균열 끝의 플라스틱 구역은 균열 크기와 동일한 크기의 크기를 가질 수 있다.
가해지는 하중이 증가하고 균열 길이가 증가함에 따라 플라스틱 구역의 크기와 모양이 변할 수 있다.

따라서 다음을 설명할 수 있는 탄성 플라스틱 재료에 대해 보다 일반적인 균열 성장 이론이 필요합니다.

균열 끝의 공극(붕괴)의 핵 형성, 성장 및 결합을 포함하는 초기 균열 성장을 위한 국소 조건.
추가적인 균열 성장과 불안정한 골절의 전지구 에너지 균형 기준.

CTOD

지금까지 엘라스토 플라스틱 부위의 파괴 인성 측정의 첫 번째 매개변수는 균열 팁 개구 변위(CTOD) 또는 "균열 정점의 개구부"였다.이 매개변수는 구조강 연구 중에 Wells에 의해 결정되었으며, 이는 높은 인성 때문에 선형 탄성 파괴 역학 모델로는 특성화할 수 없었다.그는 골절이 발생하기 전에 균열벽이 이탈하고^{[clarification needed]} 있었으며 균열 끝부분은 균열 후 플라스틱 변형으로 인해 급성부터 반올림까지 다양했다고 지적했다.또한 인성이 뛰어난 강철에서는 균열 팁의 둥글림이 더욱 두드러졌다.

CTOD에는 많은 대체 정의가 있습니다.가장 일반적인 두 가지 정의에서 CTOD는 원래 균열 선단에서의 변위와 90도 절편입니다.후자의 정의는 라이스에 의해 제안되었고, 그러한 유한 요소 모델에서 CTOD를 추론하는 데 일반적으로 사용된다.균열 팁이 반원 모양으로 깜박이는 경우 이 두 정의는 동일합니다.

CTOD의 대부분의 실험실 측정은 3점 벤딩으로 로드된 가장자리 균열 검체에 대해 수행되었습니다.초기 실험에서는 균열에 삽입된 평평한 패들 모양의 게이지를 사용했습니다. 균열이 열리면 패들 게이지가 회전하고 전자 신호가 x-y 플로터로 전송되었습니다.그러나 패들 게이지로 균열 선단에 도달하기 어려웠기 때문에 이 방법은 정확하지 않았습니다.현재 균열구에서의 변위 V를 측정하여 시료 반쪽이 강성이며 힌지점(균열선단)을 중심으로 회전한다고 가정하여 CTOD를 추정한다.

R-곡선

탄성-플라스틱 파괴 역학의 방향에서 초기 시도는 Irwin의 균열 연장 저항 곡선, 균열 성장 저항 곡선 또는 R-곡선이었다.이 곡선은 탄성 플라스틱 재료의 균열 크기가 커짐에 따라 내파괴성이 증가한다는 사실을 인정한다.R-곡선은 균열크기의 함수로써 총 에너지 소산률을 나타낸 그림으로, 균열크기의 성장이 느리고 불안정한 파단이 발생하는 과정을 조사하는 데 사용할 수 있다.그러나 R-곡선은 1970년대 초반까지 응용 분야에서 널리 사용되지 않았다.주된 이유는 R-곡선이 시료의 형상에 따라 달라지고 균열구동력을 ^[6]계산하기 어렵기 때문으로 보인다.

J적분

1960년대 중반 제임스 R. Rice(당시 Brown University의 Rice)와 G. P. Cherepanov는 부품이 더 이상 선형 탄성 근사치를 따르지 않는 충분한 균열 끝 변형이 있는 경우를 설명하기 위해 새로운 인성 측정을 독자적으로 개발했다.균열 팁에 앞서 비선형 탄성(또는 단조 변형 이론 플라스틱) 변형을 가정한 Rice의 분석은 ^[13]J-적분이라고 한다.이 분석은 균열 팁의 소성 변형이 하중을 받는 부품의 가장 먼 가장자리까지 확장되지 않는 경우에 한정됩니다.또한 재료의 가정된 비선형 탄성 거동이 실제 재료의 하중 반응에 대한 형태와 크기 면에서 합리적인 근사치여야 한다.탄성-플라스틱 고장 매개변수는 J로 지정되며_Ic, 본 문서 부록의 식(3.1)을 사용하여 K로_Ic 변환된다.또한 J 적분 접근법은 선형 탄성 거동에 대한 그리피스 이론으로 감소한다는 점에 유의하십시오.

J 적분의 수학적 정의는 다음과 같다.

{\displaystyle J=\int _{\Gamma }(w,dy-T_{i}{\frac {\frac u_{i}}{\int x},ds}\paret w=\int _{0}^{\varepsilon _{ij},d\varepsilon _{i})

어디에

γ

{

displaystyle

\

\Gamma

Gamma

\Gamma

}는 균열의 정점을 시계방향으로 도는 임의의 경로입니다.

\displaystyle

w는

w

변형 에너지의 밀도입니다.

(

T_

{i

})는

T_{i}

트랙션 벡터의 구성요소입니다.

u_{i}

i

u_{i}

{

display

style

u

_ {

u_{i}

i}}는

u_{i}

변위 벡터의 구성요소입니다.

\displaystyle

ds는

\displaystyle

의 증분 길이입니다.

\sigma _{ij}

i

\sigma _{ij}

\ display

style _

{

\sigma _{ij}

ij

\sigma _{ij}

} 및

\varepsilon _{ij}

i

\varepsilon _{ij}

\ display

style

\

varepsilon _

{

\varepsilon _{ij}

ij

\varepsilon _{ij}

}는 스트레스와 스트레인 텐서입니다.

엔지니어가 K를 사용하여_Ic 파괴 인성을 특성화하는 데 익숙해졌기 때문에 J를 K에 대해 감소시키는_Ic 관계가 사용되었습니다.

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

c

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

K_{Ic}={\sqrt {E^{*}J_{Ic}}}\,

c {

display style

K _ {

Ic

} =

sqrt

{

E^

{ * }

J

_ {

Ic

} , , } 。

E^{*}=E

서

K_{Ic} = \sqrt{E^* J_{Ic}}\,

평면

E^{*}={\frac {E}{1-\nu ^{2}}}

에

E^{*}=E

는

E^* = E

E

E^{*}=E

E^{*}={\frac {E}{1-\nu ^{2}}}

E^{*}={\frac {E}{1-\nu ^{2}}}

E^{*}=E

=

E^{*}={\frac {E}{1-\nu ^{2}}}

∗

1

E^{*}={\frac {E}{1-\nu ^{2}}}

-

E^{*}={\frac {E}{1-\nu ^{2}}}

{

E^{*}={\frac {E}{1-\nu ^{2}}}

}

응집성 구역 모델

균열 팁 주변의 상당한 영역이 소성변형을 겪었을 경우, 균열의 추가 확대 가능성 및 균열의 성장 및 분기 방향을 결정하기 위해 다른 방법을 사용할 수 있다.수치 계산에 쉽게 통합되는 간단한 기술은 1960년대 초 바렌블랫과^[14] 더그데일에^[15] 의해 독립적으로 제안된 개념에 기초한 응집 구역 모델 방법이다.더그데일-배런블랫 모형과 그리피스의 이론 사이의 관계는 1967년 ^[16]윌리스에 의해 처음 논의되었다.1968년 ^[13]라이스는 메짐성 골절의 맥락에서 두 접근법의 동등성을 보여주었다.

전환 결함 크기

균열크기의 함수로서의 고장응력

재료에 항복강도 $\sigma _{Y}$ Y $(\$ style _ ${Y})$ 와 $\sigma_Y$ 모드 I $K_{Ic}$ c(\ $display$ $style$ K_ ${Ic$ 의 파단 인성을 부여합니다.파단역학에 따라 재료는 응력 $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ fail $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ $display$ style $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ \ $dgeal$ _{\fail} $\sigma _{\text{fail}}=K_{Ic}/{\sqrt {\pi a}}$ = $K_{Q}$ {rtext{{rate}} {Rt}/{Rt}에서 파괴됩니다. $\sigma _{fail}=\sigma _{Y}$ 는 " $\sigma _{fail}=\sigma _{Y}$ $\sigma _{fail}=\sigma _{Y}$ i $=$ " $\sigma _{fail}=\sigma _{Y}$ { $displaystyle \displaystyle$ _ ${fail$ }=\ $display$ _ ${Y$ 일 때 산출됩니다.이러한 곡선은 a $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ 2 / $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ 2 {\ $displaystyle$ a $=K_{$ Ic $}^{2}/\pi$ \ $display_$ { $Y$ $}^2}$ 일 때 교차합니다 $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ $a=K_{Ic}^{2}/\pi \sigma _{Y}^{2}$ {\ $displaystyle$ a}의 $a$ $값$ 을t {\ $displaystyle a_{t}}}$ 라고 하며 $a_{t}$ 의 재료 특성에 따라 달라집니다. $a<a_{t}$ < $a<a_{t}$ < $displaystyle$ a < $a$ { $t$ the 、 a $a>a_{t}$ > $a>a_{t}$ < $displaystyle$ a > a _ { $t$ } $a>a_{t}$ 、 fracture mechanics fracture when when when 。엔지니어링 합금의 t $(\$ $a_{t}$ 은 $a_{t}$ 100mm이고 세라믹의 경우 0.001mm입니다.^{[citation needed]}제조 공정에서 마이크로미터의 순서로 결함이 발생할 수 있다고 가정하면, 세라믹은 파괴에 의해 고장날 가능성이 높은 반면 엔지니어링 합금은 소성 변형에 의해 고장날 가능성이 높다는 것을 알 수 있습니다.

「」를 참조해 주세요.

AFGROW – 파괴 역학 및 피로 균열 성장 분석 소프트웨어
콘크리트 파단해석 – 콘크리트의 파단역학에 관한 연구
지진 – 지각의 급격한 움직임
피로 – 반복하중에 의한 재료 균열의 시작 및 전파
단층(지질) – 암석의 균열 또는 불연속성(변위)
노치(엔지니어링) – 평면 재료의 외부 생성 움푹 패인 부분
페리디나믹스, 불연속성을 가진 변형, 특히 파열을 지향하는 연속체 역학의 공식
충격(메트릭) – 갑작스러운 과도 가속
재료의 강도 – 응력과 변형에 노출되는 고체 물체의 거동
응력 부식 균열 – 부식 환경에서의 균열 성장
구조 파괴 역학 – 구조 공학 분야

레퍼런스

^ T.L. Anderson (1995). Fracture Mechanics: Fundamentals and Applications. CRC Press. ISBN 978-0849316562.
^ ^a ^b H.L. Ewalds; R.J.H. Wanhill (1984). Fracture Mechanics. Edward Arnold and Delftse Uitgevers Maatschappij. ISBN 978-0-7131-3515-2.
^ McMeeking, Robert M. (May 2004). "The energy release rate for a Griffith crack in a piezoelectric material". Engineering Fracture Mechanics. 71 (7–8): 1149–1163. doi:10.1016/S0013-7944(03)00135-8.
^ Lenci, Stefano (2001). "Analysis of a crack at a weak interface". International Journal of Fracture. 108 (3): 275–290. doi:10.1023/A:1011041409243. S2CID 115306909.
^ 를 클릭합니다Griffith, A. A. (1921), "The phenomena of rupture and flow in solids", Philosophical Transactions of the Royal Society of London, A, 221 (582–593): 163–198, Bibcode:1921RSPTA.221..163G, doi:10.1098/rsta.1921.0006.
^ ^a ^b ^c E. 에르도안(2000) 파괴 역학, 국제 고체 및 구조 저널, 37, 페이지 171–183.
^ ^a ^b Irwin G(1957), 판을 가로지르는 균열 끝 부근의 응력 및 변형률 분석, Journal of Applied Mechanics 24, 361–364.
^ 오로완, E., 1949년고형물의 파괴 및 강도.물리학 XII의 진보에 관한 보고서, 185–232.
^ ^a ^b Liu, M.; et al. (2015). "An improved semi-analytical solution for stress at round-tip notches" (PDF). Engineering Fracture Mechanics. 149: 134–143. doi:10.1016/j.engfracmech.2015.10.004.
^ ^a ^b Weisshaar, Terry (July 28, 2011). Aerospace Structures- an Introduction to Fundamental Problems. West Lafayette, IN: Purdue University.
^ "Crack Tip Plastic Zone Size". Handbook for Damage Tolerant Design. LexTech, Inc. Retrieved 20 November 2016.
^ "Retardation". Handbook for Damage Tolerant Design. LexTech, Inc. Retrieved 20 November 2016.
^ ^a ^b 를 클릭합니다Rice, J. R. (1968), "A path independent integral and the approximate analysis of strain concentration by notches and cracks" (PDF), Journal of Applied Mechanics, 35 (2): 379–386, Bibcode:1968JAM....35..379R, CiteSeerX 10.1.1.1023.7604, doi:10.1115/1.3601206.
^ Barenblatt, G. I. (1962), "The mathematical theory of equilibrium cracks in brittle fracture" (PDF), Advances in Applied Mechanics, 7: 55–129, doi:10.1016/s0065-2156(08)70121-2, ISBN 9780120020072
^ Dugdale, D. S. (1960), "Yielding of steel sheets containing slits", Journal of the Mechanics and Physics of Solids, 8 (2): 100–104, Bibcode:1960JMPSo...8..100D, doi:10.1016/0022-5096(60)90013-2, S2CID 136484892
^ 를 클릭합니다Willis, J. R. (1967), "A comparison of the fracture criteria of Griffith and Barenblatt", Journal of the Mechanics and Physics of Solids, 15 (3): 151–162, Bibcode:1967JMPSo..15..151W, doi:10.1016/0022-5096(67)90029-4.

추가 정보

Buckley, C.P. "Material Failure", 강의 노트(2005), 옥스퍼드 대학교.
데이비지, R.W., Cambridge 솔리드 스테이트 사이언스 시리즈, 세라믹스의 기계적 거동(1979년)
Demaid, Adrian, Fail Safe, Open University (2004)
그린, D, 세라믹의 기계적 특성에 대한 입문, 케임브리지 솔리드 스테이트 사이언스 시리즈, Eds.클라크, D.R., 수레쉬, 사우스, 워드, I.M.(1998년)
케임브리지 고체 과학 시리즈, B.R., 부서지기 쉬운 고체의 파괴, 제2편 (1993)
Farahmand, B., Bockrath, G. 및 Glassco, J. (1997년) 고위험 부품의 피로 및 파괴 역학, Chapman & Hall.ISBN 978-0-412-12991-9.
Chen, X., Mai, Y.-W, 전자파 재료의 파괴역학: 비선형 자기장 이론과 응용, 임페리얼 칼리지 프레스, (2012)
A.N. 젠트, W.V. 마스, 수신: 제임스 E.Mark, Burak erman and Mike Roland 편집자, 제10장 – 고무의 강도, 제4판, 학술 출판사, 보스턴, 2013년, 페이지 473-516, ISBN 9780123945846, 10.1016/B978-1245000-3984
젠더, 앨런Fracture Mechanics, SpringerLink, (2012).

외부 링크

비선형 파단 역학에 대한 교수님의 설명.하버드 대학교 존 허친슨
박막의 파괴와 다층화에 관한 교수님의 주의사항.하버드 대학교 존 허친슨
네덜란드, TU 에인트호벤, Piet Schreurs의 파괴 역학

[anderson-1] T.L. Anderson (1995). Fracture Mechanics: Fundamentals and Applications. CRC Press. ISBN 978-0849316562.

[ewalds-2] H.L. Ewalds; R.J.H. Wanhill (1984). Fracture Mechanics. Edward Arnold and Delftse Uitgevers Maatschappij. ISBN 978-0-7131-3515-2.

[3] McMeeking, Robert M. (May 2004). "The energy release rate for a Griffith crack in a piezoelectric material". Engineering Fracture Mechanics. 71 (7–8): 1149–1163. doi:10.1016/S0013-7944(03)00135-8.

[4] Lenci, Stefano (2001). "Analysis of a crack at a weak interface". International Journal of Fracture. 108 (3): 275–290. doi:10.1023/A:1011041409243. S2CID 115306909.

[griffith21-5] 를 클릭합니다Griffith, A. A. (1921), "The phenomena of rupture and flow in solids", Philosophical Transactions of the Royal Society of London, A, 221 (582–593): 163–198, Bibcode:1921RSPTA.221..163G, doi:10.1098/rsta.1921.0006.

[Erdogan00-6] E. 에르도안(2000) 파괴 역학, 국제 고체 및 구조 저널, 37, 페이지 171–183.

[Irwin57-7] Irwin G(1957), 판을 가로지르는 균열 끝 부근의 응력 및 변형률 분석, Journal of Applied Mechanics 24, 361–364.

[8] 오로완, E., 1949년고형물의 파괴 및 강도.물리학 XII의 진보에 관한 보고서, 185–232.

[notch-9] Liu, M.; et al. (2015). "An improved semi-analytical solution for stress at round-tip notches" (PDF). Engineering Fracture Mechanics. 149: 134–143. doi:10.1016/j.engfracmech.2015.10.004.

[Purdue_University-10] Weisshaar, Terry (July 28, 2011). Aerospace Structures- an Introduction to Fundamental Problems. West Lafayette, IN: Purdue University.

[11] "Crack Tip Plastic Zone Size". Handbook for Damage Tolerant Design. LexTech, Inc. Retrieved 20 November 2016.

[12] "Retardation". Handbook for Damage Tolerant Design. LexTech, Inc. Retrieved 20 November 2016.

[rice-13] 를 클릭합니다Rice, J. R. (1968), "A path independent integral and the approximate analysis of strain concentration by notches and cracks" (PDF), Journal of Applied Mechanics, 35 (2): 379–386, Bibcode:1968JAM....35..379R, CiteSeerX 10.1.1.1023.7604, doi:10.1115/1.3601206.

[baren-14] Barenblatt, G. I. (1962), "The mathematical theory of equilibrium cracks in brittle fracture" (PDF), Advances in Applied Mechanics, 7: 55–129, doi:10.1016/s0065-2156(08)70121-2, ISBN 9780120020072

[dug-15] Dugdale, D. S. (1960), "Yielding of steel sheets containing slits", Journal of the Mechanics and Physics of Solids, 8 (2): 100–104, Bibcode:1960JMPSo...8..100D, doi:10.1016/0022-5096(60)90013-2, S2CID 136484892

[willis-16] 를 클릭합니다Willis, J. R. (1967), "A comparison of the fracture criteria of Griffith and Barenblatt", Journal of the Mechanics and Physics of Solids, 15 (3): 151–162, Bibcode:1967JMPSo..15..151W, doi:10.1016/0022-5096(67)90029-4.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

v t 연속체 역학의 토픽
디비전	고체 역학 유체역학 음향학 진동 강체 역학
법률과 정의	법률 질량 보존 운동량 보존 나비에스토크스 베르누이 푸아세유 아르키메데스 파스칼 에너지 절약 엔트로피 부등식 정의들 스트레스 코시 강세 스트레스 측정 변형 작은 변종 반평면 전단 큰 변종 호환성.
솔리드 및 구조 역학	솔리드 탄력성 선형의 후크의 법칙 횡등방성 직교성 초탄성 막탄성 상태 방정식 휴고니오 JWL 저탄성 코시 탄성 점탄성 크리프 콘크리트 크리프 소성 암괴 소성 점소성 수율기준 브레슬러피스터 컨택 메카니즘 마찰 없음 마찰 재료고장론 드러커 안정성 재료고장론 피로 파괴 역학 J적분 콤팩트 장력 시료 데미지 존슨 홀름퀴스트 구조물들 구부러지다 굽힘 모멘트 판의 굽힘 샌드위치 이론
유체역학	유체 유체 정전기 유체 역학 나비에-스토크스 방정식 베르누이의 원리 푸아세유 방정식 부력 점성 뉴턴의 비뉴욕인 아르키메데스의 원리 파스칼의 법칙 압력. 액체 표면 장력 모세관 작용 가스 대기. 보일의 법칙 샤를의 법칙 게이-루삭의 법칙 복합가스 법칙 플라즈마
음향학	음향 이론 에어로어쿠스틱스
레올로지	점탄성 스마트 유체 자기 지질학 전기기후학 강유체 레오메트리 레오미터
과학자	베르누이 보일 코시 찰스 오일러 게이루삭 후크 파스칼 뉴턴 경이다. 나비에 스토크스
어워드	§ 잉겐 메달 윌리엄 프라거 메달

Search

파괴 역학

네임스페이스

더

목차

동기

선형탄성파괴역학

그리피스 기준

어윈의 수정

응력 강도 계수

변형 에너지 방출

균열 선단 플라스틱 구역

제한 사항

탄성-소성 파괴 역학

CTOD

R-곡선

J적분

응집성 구역 모델

전환 결함 크기

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

파괴 역학

동기

선형탄성파괴역학

그리피스 기준

어윈의 수정

응력 강도 계수

변형 에너지 방출

균열 선단 플라스틱 구역

제한 사항

탄성-소성 파괴 역학

CTOD

R-곡선

J적분

응집성 구역 모델

전환 결함 크기

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.