연속체 역학에서 어떤 물질은 특정 평면에 걸쳐 응력 벡터가 0이면 평면에 응력을 받는다고 한다. 그러한 상황이 얇은 판의 경우처럼 구조물의 전체 요소에 걸쳐 발생할 때, 스트레스 상태는 치수 2의 텐서(3 × 3이 아닌 2 × 2 행렬로 표현됨)로 나타낼 수 있기 때문에 스트레스 분석이 상당히 단순화된다. [1] 관련 개념인 평면 스트레인은 종종 매우 두꺼운 구성원에게 적용된다.
평면 응력은 일반적으로 얇은 평판에서 발생하며, 평면에 평행한 하중력에 의해서만 작용한다. 어떤 상황에서는 완만하게 휘어진 얇은 판도 응력 분석을 목적으로 평면 응력을 갖는다고 가정할 수 있다. 예를 들어 압력을 받는 액체로 채워진 박벽 실린더가 이에 해당한다. 이러한 경우 플레이트에 수직인 응력 구성요소는 플레이트에 평행한 구성요소에 비해 무시할 수 있다.[1]
그러나 다른 상황에서는 얇은 판의 휨응력을 무시할 수 없다. 여전히 2차원 도메인을 사용해 분석을 단순화할 수 있지만 각 지점의 평면 응력 텐서는 굴절 용어로 보완해야 한다.
수학적 정의
수학적으로 재료의 어느 지점에서 발생하는 응력은 3가지 주요 응력 중 하나(Cauchy 응력 텐서의 고유값)가 0이면 평면응력이다. 즉, 스트레스 텐서가 형태를 갖는 데카르트 좌표계가 있다.

를 들어,  y
y  및 을 따라 10, 40 및 5cm 크기의 직사각형 블록을 고려하십시오
및 을 따라 10, 40 및 5cm 크기의 직사각형 블록을 고려하십시오 이 블록은 x x 방향으로
이 블록은 x x 방향으로
 확장되고 y } 방향으로 되고 있다.udes 10 N과 20 N은 각각 해당 면에 균일하게 분포한다. 블록 내부의 응력 텐서는
확장되고 y } 방향으로 되고 있다.udes 10 N과 20 N은 각각 해당 면에 균일하게 분포한다. 블록 내부의 응력 텐서는

보다 일반적으로 처음 두 좌표 축을 임의로 선택하지만 0 응력 방향과 수직인 경우 응력 텐서는 형태를 갖게 된다.

따라서 2 × 2 행렬로 나타낼 수 있다.

구성 방정식
- Hoke의 법칙#Plane_stress 참조
곡선 표면에서의 평면 응력
어떤 경우에는 평면 응력 모델을 사용하여 부드럽게 곡선된 표면을 분석할 수 있다. 예를 들어, 림을 따라 균일하게 분포하고 가압 유체로 채워진 축압하중을 받는 얇은 벽면 실린더를 고려하십시오. 내부 압력은 벽에 반응 후프 응력을 발생시키며, 실린더 축에 수직으로 지시되고 표면과 접선되는 정상적인 인장응력을 발생시킨다. 실린더는 한 방향의 인장하중과 다른 방향의 압축하중을 받는 평평한 얇은 직사각형 판으로서, 두 방향 모두 플레이트에 평행하게, 개념적으로 연접되지 않고 분석할 수 있다.
평면 변형률(스트레인 행렬)
한 치수가 다른 치수에 비해 매우 큰 경우, 가장 긴 치수의 방향에서 주 변형이 구속되고 상수로 가정될 수 있으며, 이는 변형을 따라 효과적으로 제로 변형이 발생하여 평면 변형 조건이 발생함을 의미한다(그림 7.2). 이 경우 모든 주응력이 0이 아니지만 가장 긴 치수의 방향에서 주응력은 계산을 무시할 수 있다. 따라서, 예를 들어 저수지에 의해 적재된 단면에서 분석된 댐과 같은 스트레스의 2차원 분석을 허용한다.
해당 변형률 텐서는 다음과 같다.

여기서 0이 아닌 33 용어는 포아송 효과에서 발생한다. 이 변형 항은 응력 분석에서 일시적으로 제거되어 평면 내 항만 남길 수 있으므로 분석을 2차원으로 효과적으로 줄일 수 있다.[1]
포아송 효과에서 발생한다. 이 변형 항은 응력 분석에서 일시적으로 제거되어 평면 내 항만 남길 수 있으므로 분석을 2차원으로 효과적으로 줄일 수 있다.[1]
평면응력과 평면변형의 응력변환
평면 응력 또는 평면 변형 상태의 에서 스트레스 구성 요소 _ y, y와
구성 요소 _ y, y와 기타 모든 스트레스 구성 요소가 0과 같은 점을 고려하십시오(그림 8.1). From static equilibrium of an infinitesimal material element at
기타 모든 스트레스 구성 요소가 0과 같은 점을 고려하십시오(그림 8.1). From static equilibrium of an infinitesimal material element at  (Figure 8.2), the normal stress
(Figure 8.2), the normal stress  and the shear stress
and the shear stress  on any plane perpendicular to the
on any plane perpendicular to the  -
- plane passing through
plane passing through  with a unit vector
with a unit vector  making an angle of
making an angle of  with the horizontal, i.e.
with the horizontal, i.e.  is the direction cosine in the
is the direction cosine in the  방향(direction(방향:
방향(direction(방향:


These equations indicate that in a plane stress or plane strain condition, one can determine the stress components at a point on all directions, i.e. as a function of  , if one knows the stress components
, if one knows the stress components  on any 그 지점에서 두 개의 수직 방향
on any 그 지점에서 두 개의 수직 방향  - 평면과
- 평면과 평행한 방향으로 최소 요소의 단위 영역을 고려하고 있음을 명심해야 한다.
평행한 방향으로 최소 요소의 단위 영역을 고려하고 있음을 명심해야 한다.

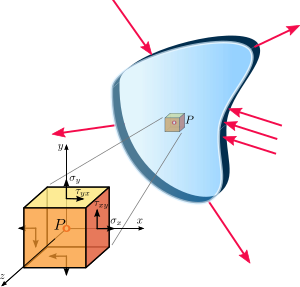
그림 8.1 - 평면 응력 조건에서 연속체의 한 지점에서 응력 변환. 
그림 8.2 - 평면 응력 조건 하에서 연속체의 한 지점을 통과하는 평면의 응력 구성 요소. 주요 방향(그림 8.3), 즉 전단 응력 구성요소가 0인 평면의 방향은 전단 응력 에 대한 이전 방정식을 0과 동일하게 만들어 얻을 수 있다. 따라서 다음과 같은 이점을 얻을 수 있다.
만들어 얻을 수 있다. 따라서 다음과 같은 이점을 얻을 수 있다.

그리고 우리는 얻는다.

이 방정식은 의 두 값을 정의하며, 이 값은 이다
이다 (그림 8.3). The same result can be obtained by finding the angle
(그림 8.3). The same result can be obtained by finding the angle  which makes the normal stress
which makes the normal stress  a maximum, i.e.
a maximum, i.e. 
The principal stresses  and
and  , or minimum and maximum normal stresses
, or minimum and maximum normal stresses  and
and  , respectively, can then be obtained by replacing both values of
, respectively, can then be obtained by replacing both values of  into the previous equation for
into the previous equation for  . This can be achieved by rearranging the equations for
. This can be achieved by rearranging the equations for  and
and  먼저 첫 번째 방정식의 첫 번째 용어를 바꾸어 각 방정식의 양쪽을 제곱한 다음 그것들을 추가한다. 그래서 우리는
먼저 첫 번째 방정식의 첫 번째 용어를 바꾸어 각 방정식의 양쪽을 제곱한 다음 그것들을 추가한다. 그래서 우리는
![\left[ \sigma_\mathrm{n} - \tfrac{1}{2} ( \sigma_x + \sigma_y )\right]^2 + \tau_\mathrm{n}^2 = \left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2 \,\!](/immutable/placeholder.png)

어디에
![R = \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2} \quad \text{and} \quad \sigma_\mathrm{avg} = \tfrac{1}{2} ( \sigma_x + \sigma_y )\,\!](/immutable/placeholder.png)
즉, 좌표가 있는 점 a , 을 중심으로 한 R 의 원의 방정식이며
한 R 의 원의 방정식이며![[\sigma_\mathrm{avg}, 0]\,\!](/immutable/placeholder.png) Mohr's circle이라 불린다. 그러나 주계약자가 전단응력 = }=을(를
Mohr's circle이라 불린다. 그러나 주계약자가 전단응력 = }=을(를 강조한다는 것을 알고 우리는 이 방정식을 통해 다음을 얻는다.
강조한다는 것을 알고 우리는 이 방정식을 통해 다음을 얻는다.
![\sigma_1 =\sigma_\mathrm{max} = \tfrac{1}{2}(\sigma_x + \sigma_y) + \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2}\,\!](/immutable/placeholder.png)
![\sigma_2 =\sigma_\mathrm{min} = \tfrac{1}{2}(\sigma_x + \sigma_y) - \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2}\,\!](/immutable/placeholder.png)

그림 8.3 - 주 응력 및 최대 및 최소 전단 응력 작용면을 보여주는 2차원 응력 변환. When  the infinitesimal element is oriented in the direction of the principal planes, thus the stresses acting on the rectangular element are principal stresses:
the infinitesimal element is oriented in the direction of the principal planes, thus the stresses acting on the rectangular element are principal stresses:  and
and  . Then the normal stress
. Then the normal stress  and shear stress
and shear stress  as a function of the principal stresses can be determined by making
as a function of the principal stresses can be determined by making  . Thus we have
. Thus we have


그런 다음 최대 전단 응력 은(는) 죄 = 1 = 1 예 \ = ^{ },\!}!}일
예 \ = ^{ },\!}!}일 그림 83)일
그림 83)일 ).
).

Then the minimum shear stress  occurs when
occurs when  , i.e.
, i.e.  (Figure 8.3):
(Figure 8.3):

참고 항목
참조
- ^ a b c 메이어스와 차울라(1999년) : "물질의 기계적인 거동," 66-75.