포아송비

재료과학과 고체역학에서, 포아송의 비$$ν${\$displaystyle \n$u }$ $$(nu)는 포아송 효과, 특정 하중 방향에 수직인 방향으로 재료의 변형(팽창 또는 수축)을 측정한 것입니다. 포아송 비율의 값은 축 변형률에 대한 가로 변형률의 비율의 음수입니다. 이러한 변경 사항의 작은 값의 경우$$ν {\displaystyle \n$u}$는 가로 신장량을 축방향 압축량으로 나눈 값입니다. 대부분의 재료는 포아송의 비율 값이 0.0에서 0.5 사이입니다. 고무와 ^[1]같이 부피 탄성률이 전단 탄성률보다 훨씬 높은 연성 재료의 경우 포아송의 비율은 0.5에 가깝습니다. 오픈셀 폴리머 폼의 경우 포아송의 비율은 거의 0에 가깝습니다. 왜냐하면 세포들이 압축적으로 붕괴되는 경향이 있기 때문입니다. 많은 전형적인 고체들은 포아송의 비율이 0.2-0.3 범위에 있습니다. 이 비율은 프랑스의 수학자이자 물리학자인 시메옹 푸아송의 이름을 따서 지어졌습니다.

기원.

포아송 비율은 물질이 압축 방향에 수직인 방향으로 팽창하는 경향이 있는 현상인 포아송 효과의 척도입니다. 반대로 소재를 압축하는 것이 아니라 신축하는 경우, 신축하는 방향에 대해 가로 방향으로 수축하는 경향이 일반적입니다. 고무줄을 늘리면 눈에 띄게 얇아지는 것이 일반적인 관찰입니다. 다시 포아송 비율은 상대적 팽창에 대한 상대적 수축의 비율이 될 것이며 위와 같은 값을 가질 것입니다. 일부 드문 ^[2]경우에는 압축(또는 늘이면 확장) 시 재료가 실제로 가로 방향으로 축소되어 포아송 비율의 음의 값을 얻을 수 있습니다.

영률, 전단 탄성률 및 벌크 탄성률이 양의 값을 갖기 위해서는 안정적이고 등방성이며 선형 탄성재의 포아송비가 -1.0에서 +0.5 사이가 되어야 합니다.^[3] 대부분의 재료는 포아송의 비율 값이 0.0에서 0.5 사이입니다. 작은 변형률에서 탄성 변형된 완전한 비압축 등방성 물질은 정확히 0.5의 포아송 비율을 가질 것입니다. 대부분의 강철 및 강직 폴리머는 설계 한계(수율 전) 내에서 사용될 때 약 0.3의 값을 나타내며, 대부분 일정한 부피에서 발생하는 수율 후 변형의 경우 0.5로 증가합니다.^[4] 고무의 포아송 비율은 거의 0.5입니다. 코크의 포아송 비율은 0에 가까워 압축 시 측면 팽창이 거의 없고 유리는 0.18에서 0.30 사이입니다. 일부 물질, 예를 들어 일부 폴리머 폼,^[5][6] 종이 접기 및 특정 세포는 푸아송 비율이 음수일 수 있으며, 이를 보조 물질이라고 합니다. 이러한 보조 물질을 한 방향으로 늘리면 수직 방향으로 두꺼워집니다. 반면 탄소나노튜브, 지그재그 기반의 접힌 시트 재료,^[7][8] 벌집형 보조 메타^[9] 재료 등의 일부 이방성 재료는 특정 방향에서 0.5를 초과하는 하나 이상의 포아송 비율을 나타낼 수 있습니다.

재료가 한 방향으로만 늘어나거나 압축되었다고 가정할 때(아래 그림의 x축):

${\displaystyle \nu =-{\frac {d\varepsilon _{\mathrm {trans} }}{d\varepsilon _{\mathrm {axial} }}}=-{\frac {d\varepsilon _{\mathrm {y} }}{d\varepsilon _{\mathrm {x} }}}=-{\frac {d\varepsilon _{\mathrm {z} }}{d\varepsilon _{\mathrm {x} }}}}$

어디에

• $ν$$u}$는 결과 포아송의 비율입니다.
• ${\displaystyle {}_{}}$ trans${\$displaystyle \varepsilon _{\mathrm {trans}}}는 가로 변형입니다.
• ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{축}}_{}}${\displaystyle \varepsilon _{\mathrm {axial}}}는 축 변형입니다.

양의 변형률은 확장을 나타내고 음의 변형률은 수축을 나타냅니다.

기하학적 변화에 따른 포아송의 비율

길이변화

δ$L$ ${\$$displaystyle$ \Delta L$}$의 x 방향 길이 증가와 δL$'의$y 방향 및 z 방향 길이 ${\displaystyle {}^{}}$가 있는${\displaystyle {}^{}}$x 방향으로 늘어진 정육면체(그림 1 참조)의 경우, 무한대$$대각선 변형은 다음과 같이 주어집니다.

${\displaystyle d\varepsilon _{x}={\frac {dx}{x}}\qquad d\varepsilon _{y}={\frac {dy}{y}}\qquad d\varepsilon _{z}={\frac {dz}{z}}.}$

변형을 통해 포아송의 비율이 일정한 경우, 이 식을 통합하여 포아송의 비율의 정의를 사용하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle -\nu \int _{L}^{L+\Delta L}{\frac {dx}{x}}=\int _{L}^{L+\Delta L'}{\frac {dy}{y}}=\int _{L}^{L+\Delta L'}{\frac {dz}{z}}.}$

δ$L$ {\displaystyle \$Delta$ L$}$과$$δL$' {\displaystyle$ \Delta L'} 사이의 관계를 풀이하고 지수화하면 다음과$$같습니다.

${\displaystyle \left(1+{\frac {\Delta L}{L}}\right)^{-\nu }=1+{\frac {\Delta L'}{L}}.}$

δ$L$ {\displaystyle \$Delta$ L} ${\displaystyle {}^{}}$δL$' {\displaystyle$ $\backslash$Delta L'}의 매우$$작은 값의 경우 1차 근사치가 다음과 같이 산출됩니다.

${\displaystyle \nu \approx -{\frac {\Delta L'}{\Delta L}}.}$

부피변화

이제 재료의 신축으로 인한 정육면체의 부피 δV/V의 상대적인 변화를 계산할 수 있습니다. $V$ = ${\displaystyle {}^{}}$ ${\$$displaystyle$ V = $L^{$3}} 및 V + δ V = (L + δ L ) (L + δ L') 2 {\displaystyle V+\Delta V = (L+\Delta L')\left (L+\Delta L'\right)^{2} :

${\displaystyle {\frac {\Delta V}{V}}=\left(1+{\frac {\Delta L}{L}}\right)\left(1+{\frac {\Delta L'}{L}}\right)^{2}-1}$

${\displaystyle 위}$에서 도출한$$δ$L$ {\displaystyle$$\$Delta$ L}과$$δL'${\displaystyle$ $\backslash$Delta L'} 사이의 관계를 사용합니다.

${\displaystyle {\frac {\Delta V}{V}}=\left(1+{\frac {\Delta L}{L}}\right)^{1-2\nu}-1}$

그리고$$매우 작은$$δ$$L {\$displaystyle$ \${\displaystyle {}^{}}$ L}${\displaystyle {}^{}}$및$$δ L' {\$displaystyle$ $\backslash$Delta L'} 값의 경우 1차 근사치가 산출됩니다.

${\displaystyle {\frac {\Delta V}{V}\approx (1-2\n)u ){\frac {\Delta L}{L}}}$

등방성 물질의 경우 라메의 관계식을^[10] 사용할 수 있습니다.

${\displaystyle \nu \approx {\frac {1}{2}}-{\frac {E}{6K}}}$

여기서 $K{\displaystyle }$ ${\displaystyle K}$는 벌크 모듈러스이고 $E{\displaystyle }${\$displaystyle$ E$}$는 영 모듈러스입니다.

폭변화

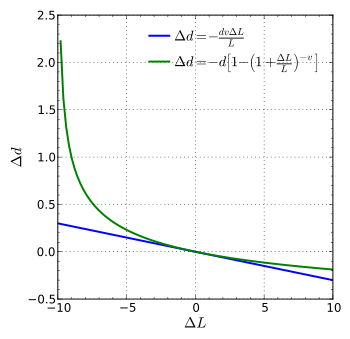
직경(또는 폭, 또는 두께)이 d이고 길이가 L인 막대가 장력을 받아 길이가 δL만큼 변화하면 직경 d는 다음과 같이 변화합니다.

${\displaystyle {\Delta \over d} = -\nu {\frac {\Delta L}{L}}}$

위의 공식은 작은 변형의 경우에만 해당되며, 변형이 크면 다음과 같은 (더 정확한) 공식을 사용할 수 있습니다.

${\displaystyle \Delta d=-d\left(1-{\left(1+{\frac {\Delta L}{L}}\right)}^{-\nu}\right)}$

어디에

• ${\displaystyle d}$ ${\displaystyle$ d$}$이(가) 원래 직경입니다.
• ${\displaystyle$ \Delta} 가 로드 직경 변경입니다.
• $ν$$u}$은(는) 포아송의 비율입니다.
• ${\displaystyle L}$ ${\displaystyle L}$은(는) 원래 길이이며, 스트레치 전입니다.
• ${\displaystyle$ \DeltaL}은 길이의 변화입니다.

길이가 증가함에 따라 감소하므로 값이 음수입니다.

특징소재

등방성

압축력(즉, 정상적인) 힘만을 받는 선형 등방성 재료의 경우, 한 축 방향으로 재료가 변형되면 다른 축을 따라 3차원으로 재료가 변형됩니다. 따라서 훅의 법칙(압축력의 경우)을 세 가지 차원으로 일반화할 수 있습니다.

${\displaystyle \varepsilon_{xx}={\frac {1}{E}}\left[\sigma_{xx}-\nu \left(\sigma _{y}+\sigma _{zz}\right)}$

${\displaystyle \varepsilon_{y}={\frac {1}{E}}\left[\sigma_{y}-\nu \left(\sigma _{xx}+\sigma _{zz}\right)\right]}$

${\displaystyle \varepsilon_{zz}={\frac {1}{E}}\left[\sigma_{z}-\nu \left(\sigma _{xx}+\sigma _{yy}\right)\right]}$

위치:

• ${\displaystyle \varepsilon _{xx}}$, ${\displaystyle \varepsilon _{yy}}$, and ${\displaystyle \varepsilon _{zz}}$ are strain in the direction of ${\displaystyle x}$, ${\displaystyle y}$ and ${\displaystyle z}$ axis
• ${\displaystyle \sigma _{xx}}$, ${\displaystyle \sigma _{yy}}$, and ${\displaystyle \sigma _{zz}}$ are stress in the direction of ${\displaystyle x}$, ${\displaystyle y}$ and ${\displaystyle z}$ axis
• ${\displaystyle E}$ ${\displaystyle E}$은(등방성 재료의$$ 경우 $x{\displaystyle }$ ${\displaystyle$ x$\},$ $y{\displaystyle }$ ${\displaystyle$ y$}$및 $z{\displaystyle }$ ${\displaystyle$ z$}$의 $모든$ 방향에서 동일) 영률입니다.
• $ν$$u}$은(등방성 재료의$$ 경우 $x{\displaystyle }$ ${\displaystyle$ x$\},$ $y{\displaystyle }$ ${\displaystyle$ y$}$ 및$$ $z{\displaystyle }$ ${\displaystyle$ z$}$의 포아송 $비율$입니다.)

이 방정식들은 모두 다음과 같이 합성될 수 있습니다.

${\displaystyle \varepsilon_{ii}={\frac {1}{E}}\left[\sigma_{ii}(1+\n)u )-\nu \sum _{k}\sigma _{kk}\right]}$

가장 일반적인 경우에는 전단 응력도 정상 응력과 마찬가지로 유지되며, 후크 법칙의 완전한 일반화는 다음과 같이 주어집니다.

${\displaystyle \varepsilon _{ij}={\frac {1}{E}}\left[\sigma _{ij}(1+\nu )-\nu \ delta _{ij}\sum _{k}\sigma _{kk}\right]}$

여기서$$δ ij ${\displaystyle \delta$ _{ij}}는 크로네커 삼각주입니다. 아인슈타인 표기법은 일반적으로 다음과 같이 채택됩니다.

${\displaystyle \sigma _{kk}\equiv \sum _{l}\delta _{kl}\sigma _{kl}}$

방정식을 간단히 다음과 같이 적습니다.

${\displaystyle \varepsilon _{ij}={\frac {1}{E}}\left[\sigma _{ij}(1+\nu )-\nu \delta _{ij}\sigma _{kk}\right]}$

이방성

비등방성 재료의 경우 포아송 비율은 확장 및 가로 변형 방향에 따라 달라집니다.

${\displaystyle \nu (\mathbf {n},\mathbf {m})=-E\left(\mathbf {n} \right)s_{ij\alpha \beta }n_{i}n_{j}m_{\alpha }m_{\beta }$

${\displaystyle E^{-1}(\mathbf {n})= s_{ij\alpha \beta }n_{i}n_{j}n_{\alpha }n_{\beta }$

$여기$서$$ν {\displaystyle \n$u}$는 포아송의 비율, $E{\displaystyle }$ ${\displaystyle$ E$}$는 영률, n ${\$은 확장 방향을 따라 향하는 단위 벡터, $m{\displaystyle \mathbf{}}${\$displaystyle \mathbf {m}$은 확장 방향에 수직으로 향하는 단위 벡터입니다. 포아송의 비율은 이방성의 종류에 따라 특별한 방향의 수가 다릅니다.^[11][12]

정사향성

직교성 재료는 재료 특성에 있어서 세 개의 서로 수직인 대칭면을 가지고 있습니다. 예를 들어, 곡물을 따라 가장 뻣뻣하고(강하며) 다른 방향에서는 덜 뻣뻣한 나무가 있습니다.

그렇다면 후크의 법칙은 행렬 형태로 표현할 수 있습니다^[13][14].

${\displaystyle {\begin{bmatrix}\epsilon_{xx}\\epsilon_{y}\\epsilon_{zz}\\2\epsilon_{zx}\2\epsilon_{xy}\end{bmatrix}}={\tfrac {1}{E_{x}}&-{\tfrac {\nu_{yx}}{E_{y}}&-{\tfrac {\nu _{zx}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xy}}{E_{x}}}&{\tfrac {1}{E_{y}}}&-{\tfrac {\nu _{zy}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xz}}{E_{x}}}&-{\tfrac {\nu _{yz}}{E_{y}}}&{\tfrac {1}{E_{z}}}&0&0&0\\0&0&0&{\tfrac {1}{G_{yz}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{zx}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{xy}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}\\\sigma _{yy}\\\sigma _{zz}\\\\sigma _{yz}\\\\sigma _{zx}\\\sigma _{xy}\end{bmatrix}}}$

어디에

• ${\displaystyle {Ei}_{}}$ ${\$는 축 $i{\displaystyle }$ ${\displaystyle$ i$}$에 따른 영률입니다.
• ${\displaystyle {\mathrm{Gij}}_{}}$ ${\$는 법선이 $i{\displaystyle }$ 방향인 평면에서$$ $j{\displaystyle }$ 방향 ${\$$displaystyle j$$}$의 전단 탄성 계수입니다$.$
• $ν$$u_{ij}}$는 $방향{\displaystyle }$ i ${\displaystyle i}$로 확장을 적용했을$$ 때 방향 $j{\displaystyle }$ ${\displaystyle j}$의 수축에 해당하는 포아송 비율입니다$.$

각 방향(x, y, z)에서 직교성 재료의 포아송 비율이 다릅니다. 그러나 응력 텐서와 변형 텐서의 대칭성은 방정식에서 6개의 포아송 비율이 모두 독립적인 것은 아님을 의미합니다. 독립적인 재료 특성은 탄성 모듈리 3개, 전단 모듈리 3개, 포아송비 3개 등 9개에 불과합니다. 나머지 세 개의 포아송 비율은 관계식에서 구할 수 있습니다.

${\displaystyle {\frac {\nu_{yx}}{E_{y}}}={\frac {\nu _{xy}}{E_{x}}}~,\qquad {\frac {\nu _{zx}}{E_{z}}}={\frac {\nu _{xz}}{E_{x}}}~,\qquad {\frac {\nu _{yz}}{E_{y}}}={\frac {\nu_{zy}}{E_{z}}}$

위의 관계를 통해 Ex > {\$displaystyle E_{x}>$일 경우$E_{y}}$ 다음$ν$ y >$ν$ x {\displaystyle \n$u_{xy}>\n$$u_{yx$ 포아송의 비율이 클수록(이 경우 xy${\displaystyle$ \n ν)$u_{xy$은$($ 경우 $ν$y x ${\displaystyle$ \n) 큰 포아송의 비율이라고 합니다.$u_{yx$는 마이너 포아송 비율이라고 합니다. 우리는 다른 포아송의 비율 사이에 유사한 관계를 찾을 수 있습니다.

가로등방성

횡방향 등방성 물질은 탄성 특성이 등방성인 등방성 평면을 가지고 있습니다. 이 등방성의 평면을 $y{\displaystyle }$- ${\displaystyle z}$ ${\displaystyle$ y - $z}$라고 가정하면$,$ 훅의 법칙은 다음과^[15] 같은 형태를 취합니다.

${\displaystyle {\begin{bmatrix}\epsilon_{xx}\\epsilon_{y}\\epsilon_{zz}\\2\epsilon_{zx}\2\epsilon_{xy}\end{bmatrix}}={\tfrac {1}{E_{x}}&-{\tfrac {\nu_{yx}}{E_{y}}&-{\tfrac {\nu _{zx}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xy}}{E_{x}}}&{\tfrac {1}{E_{y}}}&-{\tfrac {\nu _{zy}}{E_{z}}}&0&0&0\\-{\tfrac {\nu _{xz}}{E_{x}}}&-{\tfrac {\nu _{yz}}{E_{y}}}&{\tfrac {1}{E_{z}}}&0&0&0\\0&0&0&{\tfrac {1}{G_{\rm {yz}}}}&0&0\\0&0&0&0&{\tfrac {1}{G_{\rm {zx}}}}&0\\0&0&0&0&0&{\tfrac {1}{G_{\rm {xy}}}\\\end{bmatrix}}{\begin{bmatrix}\sigma _{xx}\\\\sigma _{y}\\\sigma _{y}\\\sigma _{yz}\\\\sigma _{zx}\\\sigma _{xy}\end{bmatrix}}}$

등방성 $y{\displaystyle }$- ${\displaystyle z}$ ${\displaystyle y-z}$의 평면을 사용하여 상수의 수를 줄였습니다. $즉$, ${\displaystyle {\mathrm{Ey}}_{}}$ =${\displaystyle {Ez}_{}}$, ν x$$= ν x ${\displaystyle$ E_{y} = E_{z}, ~\n$u_{xy}=\n$$u_{xz},~\n$$u_{yx}=\n$$u_{zx$

응력과 변형 텐서의 대칭성은 다음을 의미합니다.

${\displaystyle {\frac {\nu _{xy}}{E_{x}}}={\frac {\nu_{yx}}{E_{y}}~,~~\nu_{yz}=\nu_{zy}~.}$

이렇게 하면 6개의 독립 상수 ${\displaystyle {Ex}_{}}$ ${\displaystyle Y_{}}$ ${\displaystyle {\mathrm{Gxy}}_{}}$ ${\displaystyle {\mathrm{Gyz}}_{}{}_{}}$ν ${\displaystyle {\mathrm{xy}}_{}}$,$$νyz ${\displaystyle$ E_{x}가 됩니다.$E_{y},G_{xy},G_{yz},\n$$u_{xy}\n$$u_{yz$ 그러나 횡방향 등방성은 ${\displaystyle {\mathrm{Gyz}}_{}}$ ${\displaystyle G_{yz}}$와 ${\displaystyle {\mathrm{Ey}}_{}{}_{}}$$ν$$yz$ {\displaystyle E_{y},\n 사이에 추가 제약을 발생시킵니다.$u_{yz}},$ 즉$$

${\displaystyle G_{yz}={\frac {E_{y}}{2(1+\nu_{yz}}}~.}$

따라서, 5개의 독립적인 탄성 재료 특성이 있으며, 그 중 2개는 포아송의 비율입니다. 가정된 대칭 평면의 경우$$ν x y ${\displaystyle$ \n 중 큰 값을 사용합니다.$u_{xy}}$ ${\displaystyle {및}_{}}$$ν$y x ${\displaystyle$ \n$u_{yx}}$는 장조 포아송의 비율입니다. 다른 장·단 푸아송의 비율은 같습니다.

여러 재료에 대한 포아송 비율 값

재료.	포아송비
고무의	0.4999[17]
골드	0.42–0.44
포화 점토	0.40–0.49
마그네슘	0.252–0.289
티타늄의	0.265–0.34
구리	0.33
알루미늄-	0.32
찰흙을 바르다	0.30–0.45
스테인리스 스틸	0.30–0.31
강철의	0.27–0.30
주철	0.21–0.26
모래의	0.20–0.455
구체적인	0.1–0.2
유리	0.18–0.3
금속 안경	0.276–0.409[18]
거품을 내다	0.10–0.50
코르크 마개	0.0

재료.	대칭면	${\displaystyle \nu_{\rm {xy}}$	${\displaystyle \nu _{\rm {yx}}}$	${\displaystyle \nu _{\rm {yz}}}$	${\displaystyle \nu_{\rm {zy}}$	${\displaystyle \nu _{\rm {zx}}}$	${\displaystyle \nu_{\rm {xz}}$
노멕스 벌집 심	${\displaystyle x}$- ${\displaystyle y}$ ${\displaystyle x{\text{-}} y$ $리본{\displaystyle }$ x ${\displaystyle$ x$}$ 방향$$	0.49	0.69	0.01	2.75	3.88	0.01
유리섬유 epoxy 수지	${\displaystyle x{\text{-}}y}$	0.29	0.32	0.06	0.06	0.32

음의 포아송 비율 재료

보조 재료로 알려진 일부 재료는 푸아송의 비율이 음입니다. 세로축에서 양의 변형률을 받으면 재료의 가로 변형률은 실제로 양의 변형률을 보일 것입니다(즉, 단면적을 증가시킬 것입니다). 이러한 재료의 경우, 일반적으로 독특하게 배향된 힌지 분자 결합 때문입니다. 이러한 결합이 세로 방향으로 늘어나려면 힌지가 가로 방향으로 '열려야' 하며, 이는 양의 변형을 효과적으로 보여줍니다.^[19] 이것은 또한 구조화된 방식으로 수행될 수 있으며 기계적 메타물질에 대한 재료 설계의 새로운 측면으로 이어질 수 있습니다.

연구에 따르면 일부 고체 목재 유형은 압축 크리프 테스트 중에만 푸아송 비율이 음인 것으로 나타났습니다.^[20][21] 압축크리프 실험은 초기에는 포아송의 비율이 양으로 나타나지만, 음의 값에 도달할 때까지 점차 감소합니다. 결과적으로 이것은 또한 목재에 대한 푸아송의 비율이 일정한 하중 동안 시간에 의존적임을 보여주는데, 이는 축방향과 횡방향의 변형률이 동일한 비율로 증가하지 않는다는 것을 의미합니다.

미세 구조가 조작된 매체는 푸아송의 비율이 음수일 수 있습니다. 단순한 경우에는 물질을 제거하고 주기적인 다공성 매체를 생성하는 보조성이 얻어집니다.^[22] 격자는 등방성의 경우 한계 값 -1에 무한히 가까울 수 ^[23]있는 포아송 비율의 더 낮은 값에 도달할 수 있습니다.^[24]

300개 이상의 결정 물질은 푸아송의 비율이 음입니다.^[25][26][27] 예를 들어, Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn Sr, Sb, ${\displaystyle {}_{\mathrm{}}}$ 2 ${\$ 등이$$ 있습니다.

포아송 함수

유한 변형에서 가로 및 축 변형$$ε 트랜스 ${\displaystyle \varepsilon_{\text{$trans}}와$$ε 축 {\$displaystyle \varepsilon_{\$text{axial}} 사이의 관계는 일반적으로 포아송 비율로 잘 설명되지 않습니다. 사실 포아송 비율은 큰 변형률 체제에서 적용된 변형률의 함수로 간주되는 경우가 많습니다. 이러한 경우 포아송 비율은 여러 가지 경쟁적인 정의가 있는 포아송 함수로 대체됩니다.^[28] 가로 신축 λ trans =$$ε$$trans + 1$$${\displaystyle$\lambda _{\text{trans}}=\varepsilon _{\text{trans}+1} 및 축 신축 λ 축 = ε 축 + 1 {\displaystyle \lambda _{\text{axial}}=\varepsilon _{\text{axial}+1} 정의, 여기서 가로 신축은 축 신축의 함수입니다(즉,). ${\displaystyle {}_{}}$t${\displaystyle r_{}}$a${\displaystyle n_{}}$s =${\displaystyle {}_{}{\text{λ}}_{}}$ $tr$ (${\displaystyle \lambda }$ 축) {\displayst${\displaystyle {\mathrm{yle\; \backslash l}}_{}}$ambda _{\text{tr${\displaystyle a_{}}$n${\displaystyle {\mathrm{s\}\}=\backslash l}}_{}}$ambda _{\text{tran${\displaystyle {\mathrm{s\}\}(\backslash l}}_{}}$ambda _{\text{axial}}) 가장 일반적인 함수는 Henky, Biot,Green 및 Almansi 함수입니다.

${\displaystyle {\begin{aligned}\nu^{\text{Hencky}}&=-{\frac {\ln \ lambda _{\text{trans}}{\ln \ lambda _{\text{axial}}}\[6pt]\nu^{\text{Biot}}&={\frac {1-\lambda _{\text{trans}}{\lambda _{\text{axial}-1}}\\[6pt]\nu^{\text{Green}}&={\frac{1-\lambda _{\text{trans}}^{2}}{\lambda _{\text{axial}}^{2}-1}\[6pt]\nu^{\text{Almansi}}&={\frac{\text{trans}}^{-2}-1}{1-\ _{\text{axial}}^{-2}}\end{align}}}$

포아송 효과의 응용

포아송의 효과가 상당한 영향을 미치는 한 영역은 가압관 유동에 있습니다. 파이프 내부의 공기나 액체가 높은 압력을 받으면 파이프 내부에 균일한 힘을 가하여 파이프 재료 내에 후프 응력이 발생합니다. 포아송의 효과로 인해 이 후프 응력은 파이프의 직경이 증가하고 길이가 약간 감소합니다. 특히 길이의 감소는 파이프 접합부에 눈에 띄는 영향을 줄 수 있습니다. 왜냐하면 그 효과는 직렬로 연결된 파이프의 각 섹션마다 누적될 것이기 때문입니다. 구속된 조인트가 분리되거나 그렇지 않으면 고장이 날 가능성이 있습니다.^{[citation needed]}

포아송의 효과에 대한 또 다른 응용 분야는 구조 지질학의 영역에 있습니다. 암석은 대부분의 물질과 마찬가지로 스트레스를 받는 동안 포아송의 영향을 받습니다. 지질학적인 시간 규모에서 지각의 과도한 침식이나 퇴적은 기반 암석에 큰 수직 응력을 생성하거나 제거할 수 있습니다. 이 암석은 가해진 응력의 직접적인 결과로 수직 방향으로 팽창하거나 수축하게 되며, 또한 포아송의 영향으로 수평 방향으로 변형하게 됩니다. 이러한 수평방향의 변형률 변화는 암석의 접합부 및 휴면응력에 영향을 미치거나 형성할 수 있습니다.^[29]

역사적으로 코르크는 불활성 특성, 불침투성, 유연성, 밀봉 능력 및 복원력을 포함한 다른 이유로 와인 병을 밀봉하기 위해 선택되었지만 ^[30]코르크의 포아송 비율 0은 또 다른 이점을 제공합니다. 코르크가 병에 삽입되면서 아직 삽입되지 않은 상부가 축방향으로 압축되면서 직경이 확장되지 않습니다. 병에 코르크를 삽입하는 데 필요한 힘은 코르크의 반경방향 압축으로 인해 코르크와 병 사이의 마찰에서만 발생합니다. 예를 들어, 스토퍼가 고무로 제조된 경우(포아송의 비가 약 1/2), 고무 스토퍼 상부의 반경방향 팽창을 극복하기 위해 필요한 추가적인 힘이 상대적으로 클 것입니다.

대부분의 자동차 정비사들은 당김의 장력으로 호스의 직경이 축소되어 스터브를 꽉 움켜쥐게 되므로 금속 파이프 스터브에서 고무 호스(예: 냉각수 호스)를 당기는 것이 어렵다는 것을 알고 있습니다. (이 효과는 중국의 핑거 트랩과 동일합니다.) 넓고 평평한 블레이드를 사용하는 대신 호스를 스텁에서 더 쉽게 밀어낼 수 있습니다.

참고 항목

• 선형탄성
• 훅의 법칙
• 임펄스 여기 기법
• 직교방성 소재
• 전단 탄성률
• 영률
• 열팽창계수

참고문헌

외부 링크

• 포아송 비율의 의미
• 음의 포아송 비율 재료
• 음의 포아송 비율 재료(auxetic)에 대한 더 많은 정보 2018-02-08 Wayback Machine에서 보관

변환식
균질한 등방성 선형 탄성 재료는 이들 중 임의의 두 개의 모듈리에 의해 고유하게 결정되는 탄성 특성을 갖습니다. 따라서 임의의 두 개가 주어지면 다른 탄성 모듈리는 3D 재료(표의 첫 번째 부분)와 2D 재료(두 번째 부분) 모두에 대해 제공되는 이러한 공식에 따라 계산될 수 있습니다.
3차원 공식	${\displaystyle K=\,}$	${\displaystyle E=\,}$	${\displaystyle \lambda =\,}$	${\displaystyle G=\,}$	${\displaystyle \nu =\,}$	${\displaystyle M=\,}$	메모들
${\displaystyle (K,\,E)}$			${\displaystyle {\tfrac {3K(3K-E)}{9K-E}}}$	${\displaystyle {\tfrac {3KE}{9K-E}}$	${\displaystyle {\tfrac {3K-E}{6K}}}$	${\displaystyle {\tfrac {3K(3K+E)}{9K-E}}}$
${\displaystyle (K,\,\lambda )}$		${\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}}$		${\displaystyle {\tfrac {3(K-\lambda )}{2}}$	${\displaystyle {\tfrac {\lambda }{3K-\lambda }}}$	${\displaystyle 3K-2\lambda \,}$
${\displaystyle (K,\,G)}$		${\displaystyle {\tfrac {9KG}{3K+G}}$	${\displaystyle K-{\tfrac {2G}{3}}$		${\displaystyle {\tfrac {3K-2G}{2(3K+G)}}}$	${\displaystyle K+{\tfrac {4G}{3}}$
${\displaystyle (K,\,\n)u )}$		${\displaystyle 3K(1-2\n)u )\,}$	${\displaystyle {\tfrac {3K\nu}{1+\nu}}}$	${\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\n)u )}}}$		${\displaystyle {\tfrac {3K(1-\n)u )}{1+\nu}}}$
${\displaystyle (K,\,M)}$		${\displaystyle {\tfrac {9K(M-K)}{3K+M}}}$	${\displaystyle {\tfrac {3K-M}{2}}$	${\displaystyle {\tfrac {3(M-K)}{4}}$	${\displaystyle {\tfrac {3K-M}{3K+M}}}$
${\displaystyle (E,\,\lambda )}$	${\displaystyle {\tfrac {E+3\lambda +R}{6}}$			${\displaystyle {\tfrac {E-3\lambda +R}{4}}$	${\displaystyle {\tfrac {2\lambda }{E+\lambda +R}}}$	${\displaystyle {\tfrac {E-\lambda +R}{2}}$	${\displaystyle R={\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}}$
${\displaystyle (E,\,G)}$	${\displaystyle {\tfrac {EG}{3(3G-E)}}}$		${\displaystyle {\tfrac {G(E-2G)}{3G-E}}}$		${\displaystyle {\tfrac {E}{2G}}-1}$	${\displaystyle {\tfrac {G(4G-E)}{3G-E}}}$
${\displaystyle(E,\,\n)u )}$	${\displaystyle {\tfrac {E}{3(1-2\nu )}}}$		${\displaystyle {\tfrac {E\nu}{(1+\n)u )(1-2\n)u )}}}$	${\displaystyle {\tfrac {E}{2(1+\n)u )}}}$		${\displaystyle {\tfrac {E(1-\n)u )}{(1+\n)u )(1-2\n)u )}}}$
${\displaystyle (E,\,M)}$	${\displaystyle {\tfrac {3M-E+S}{6}}}$		${\displaystyle {\tfrac {M-E+S}{4}}}$	${\displaystyle {\tfrac {3M+E-S}{8}}}$	${\displaystyle {\tfrac {E-M+S}{4M}}}$		${\displaystyle S=\pm {\sqrt {E^{2}+9M^{2}-10EM}}$ 두 가지 유효한 해결책이 있습니다. 더하기 기호는$$ν ≥ 0 {\$displaystyle$ \n으로 이어집니다.$u \geq$ 0$\}.$ 빼기 기호는 ν ≤ 0 ${\displaystyle$ \n으로 이어집니다.$u \leq$ 0$\}.$
${\displaystyle(\lambda,\,G)}$	${\displaystyle \lambda +{\tfrac {2G}{3}}$	${\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}}$			${\displaystyle {\tfrac {\lambda}{2(\lambda +G)}}}$	${\displaystyle \lambda +2G\,}$
${\displaystyle(\lambda,\,\n)u )}$	${\displaystyle {\tfrac {\lambda(1+\n)u )}{3\nu}}}$	${\displaystyle {\tfrac {\lambda(1+\n)u )(1-2\n)u )}{\nu}}}$		${\displaystyle {\tfrac {\lambda(1-2\n)u )}{2\nu}}}$		${\displaystyle {\tfrac {\lambda(1-\n)u )}{\nu}}}$	ν =$0$ ⇔ λ = 0 ${\displaystyle$ \n에서는 사용할 수 없습니다.$u = 0\좌측 화살표 \ lambda = 0}$
${\displaystyle(\lambda,\,M)}$	${\displaystyle {\tfrac {M+2\lambda }{3}}}$	${\displaystyle {\tfrac {(M-\lambda )(M+2\lambda )}{M+\lambda }}}$		${\displaystyle {\tfrac {M-\lambda}{2}}$	${\displaystyle {\tfrac {\lambda }{M+\lambda }}}$
${\displaystyle (G,\,\n)u )}$	${\displaystyle {\tfrac {2G(1+\n)u )}{3(1-2\n)u )}}}$	${\displaystyle 2G(1+\n)u )\,}$	${\displaystyle {\tfrac {2G\nu}{1-2\nu}}}$			${\displaystyle {\tfrac {2G(1-\n)u )}{1-2\nu}}}$
${\displaystyle (G,\,M)}$	${\displaystyle M-{\tfrac {4G}{3}}$	${\displaystyle {\tfrac {G(3M-4G)}{M-G}}}$	${\displaystyle M-2G\,}$		${\displaystyle {\tfrac {M-2G}{2M-2G}}}$
${\displaystyle(\n)u,\,M)}$	${\displaystyle {\tfrac {M(1+\n)u )}{3(1-\n)u )}}}$	${\displaystyle {\tfrac {M(1+\n)u )(1-2\n)u )}{1-\nu}}}$	${\displaystyle {\tfrac {M\nu}{1-\nu}}}$	${\displaystyle {\tfrac {M(1-2\n)u )}{2(1-\n)u )}}}$
2차원 공식	${\displaystyle K_{\mathrm {2D} =\,}$	${\displaystyle E_{\mathrm {2D} =\,}$	${\displaystyle \lambda _{\mathrm {2D} =\,}$	${\displaystyle G_{\mathrm {2D} =\,}$	${\displaystyle \nu _{\mathrm {2D} }=\,}$	${\displaystyle M_{\mathrm {2D} =\,}$	메모들
${\displaystyle(K_{\mathrm {2D}},\,E_{\mathrm {2D})}$			${\displaystyle {\tfrac {2K_{\mathrm {2D} }(2K_{\mathrm {2D} }-E_{\mathrm {2D} })}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }E_{\mathrm {2D} }}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }-E_{\mathrm {2D} }}{2K_{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {4K_{\mathrm {2D} }^{2}}{4K_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle(K_{\mathrm {2D}},\lambda_{\mathrm {2D})}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }(K_{\mathrm {2D} }-\lambda _{\mathrm {2D} })}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$		${\displaystyle K_{\mathrm {2D}}-\lambda _{\mathrm {2D}}}$	${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}}}$	${\displaystyle 2K_{\mathrm {2D} }-\lambda _{\mathrm {2D} }}$
${\displaystyle(K_{\mathrm {2D}},\,G_{\mathrm {2D})}$		${\displaystyle {\tfrac {4K_{\mathrm {2D} }G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D}}-G_{\mathrm {2D}}}$		${\displaystyle {\tfrac {K_{\mathrm {2D} }-G_{\mathrm {2D} }}{K_{\mathrm {2D} }+G_{\mathrm {2D} }}}}$	${\displaystyle K_{\mathrm {2D}}+G_{\mathrm {2D}}}$
${\displaystyle(K_{\mathrm {2D}}),\,\nu _{\mathrm {2D} })}$		${\displaystyle 2K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2K_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {K_{\mathrm {2D} }(1-\nu _{\mathrm {2D} })}{1+\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2K_{\mathrm {2D} }}{1+\nu _{\mathrm {2D} }}}}$
${\displaystyle(E_{\mathrm {2D}},\,G_{\mathrm {2D})}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }G_{\mathrm {2D} }}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {2G_{\mathrm {2D} }(E_{\mathrm {2D} }-2G_{\mathrm {2D} })}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D}}}} {2G_{\mathrm {2D} }}}-1}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }^{2}}{4G_{\mathrm {2D} }-E_{\mathrm {2D} }}}}$
${\displaystyle(E_{\mathrm {2D}}),\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1-\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D}}\nu _{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$	${\displaystyle {\tfrac {E_{\mathrm {2D} }}{2(1+\nu _{\mathrm {2D} })}}}$		${\displaystyle {\tfrac {E_{\mathrm {2D} }}{(1+\nu _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}}}$
${\displaystyle(\lambda_{\mathrm {2D}},\,G_{\mathrm {2D})}$	${\displaystyle \lambda_{\mathrm {2D}}+G_{\mathrm {2D}}}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(\lambda _{\mathrm {2D} }+G_{\mathrm {2D} })}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {\lambda _{\mathrm {2D} }}{\lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }}}}$	${\displaystyle \lambda _{\mathrm {2D} }+2G_{\mathrm {2D} }\,}$
${\displaystyle(\lambda_{\mathrm {2D}}),\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {\lambda_{\mathrm {2D}}(1+\n)u _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$	${\displaystyle {\tfrac {\lambda_{\mathrm {2D}}(1+\n)u _{\mathrm {2D} })(1-\nu _{\mathrm {2D} })}{\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda_{\mathrm {2D}}(1-\n)u _{\mathrm {2D} })}{2\nu _{\mathrm {2D} }}}}$		${\displaystyle {\tfrac {\lambda _{\mathrm {2D}}}{\nu _{\mathrm {2D} }}}}$	ν ${\displaystyle {\mathrm{2}}_{}}$ D = ${\displaystyle 0}$ ⇔ λ 2 D = 0 ${\displaystyle$ \n에서는 사용할 수 없습니다.$u_{\mathrm {2D} =0\좌측 화살표 \lambda _{\mathrm {2D} =0}$
${\displaystyle(G_{\mathrm {2D}}),\,\nu _{\mathrm {2D} })}$	${\displaystyle {\tfrac {G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })}{1-\nu _{\mathrm {2D} }}}}$	${\displaystyle 2G_{\mathrm {2D} }(1+\nu _{\mathrm {2D} })\,}$	${\displaystyle {\tfrac {2G_{\mathrm {2D} }\nu _{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$			${\displaystyle {\tfrac {2G_{\mathrm {2D} }}{1-\nu _{\mathrm {2D} }}}}$
${\displaystyle(G_{\mathrm {2D}},\,M_{\mathrm {2D})}$	${\displaystyle M_{\mathrm {2D}}-G_{\mathrm {2D}}}$	${\displaystyle {\tfrac {4G_{\mathrm {2D} }(M_{\mathrm {2D} }-G_{\mathrm {2D} })}{M_{\mathrm {2D} }}}}$	${\displaystyle M_{\mathrm {2D} }-2G_{\mathrm {2D} }\,}$		${\displaystyle {\tfrac {M_{\mathrm {2D} }-2G_{\mathrm {2D} }}{M_{\mathrm {2D} }}}}$