메이저 스케일

Major scale
메이저 스케일
모드I, II, III, IV, VI, VII
컴포넌트 피치
C, D, E, F, G, A, B
품질
피치 클래스 수7
최대 균등성
포르테 번호7-35
보완하다5-35
흰색 키로 시작하는 메이저 스케일

장음계(또는 이오니아 모드)는 특히 서양 음악에서 가장 일반적으로 사용되는 음계 중 하나입니다.그것은 온음계 중 하나이다.많은 음계와 마찬가지로, 그것은 7개의 음계로 구성되어 있다: 8번째 음은 첫 번째 음을 두 배 주파수로 복제하기 때문에 같은 음의 높은 옥타브라고 불린다.

쓰기 가장 간단한 메이저 스케일은 샤프나 플랫이 필요하지 않은 유일한 메이저 스케일인 C 메이저입니다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4 d e f g a b c } }

장음계는 서양 음악, 특히 일반적인 연습 기간과 대중 음악에서 중심적인 중요성을 가지고 있었다.

카르나틱 음악에서는 Sankarabharanam으로 알려져 있다.힌두스타니 클래식 음악에서는 빌라발이라고 알려져 있다.

구조.

메이저 스케일의 특징적인 전보 및 반보 패턴

장음계의 강장음(음표)에서 제2음, 제3음, 제6음, 제7음계까지의 간격을 장음이라고 [1]합니다.

메이저 스케일은 온음계입니다.장음계의 음표 사이의 간격 순서는 다음과 같습니다.

통, 통, 통, 통, 통, 통, 통, 통, 반

여기서 "half"는 전체 톤(그림에서 빨간색 u자형 곡선)을 나타내고 "half"는 반음(그림에서 [2]빨간색 각진 선)을 나타냅니다.

메이저 스케일은 하나의 톤으로 분리된2개의 동일한 테트라코드라고 볼 수 있습니다.각 테트라코드는 두 개의 온음(전체, 전체, 절반)에 이어 반음(semitone)으로 구성됩니다.

메이저 스케일은 최대 균등합니다.

축척도

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 15/4 c4-1 d-2 e-3 f-4 g-5 a-6 b-7 c-8 b-7 a-6 g-5 f-4 e-3 d-2 c-1 } }

스케일 도수는 다음과 같습니다.

삼합회 품질

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/1 <c e g>1_\markup I <d f a>_\markup ii <e g b>_\markup iii <f a c>_\markup IV <g b d>_\markup V <a c e>_\markup vi <b d f>_\markup vii° } }

각 축척도에 세워진 삼합회는 독특한 패턴을 따릅니다.로마 숫자 분석은 괄호 안에 나와 있습니다.

  • 첫 번째 : 메이저 3인조 (I)
  • 두 번째: 마이너 트라이어드 (ii)
  • 세 번째: 마이너 트라이어드(ii)
  • 제4회: 메이저 3인조 (IV)
  • 제5회: 메이저 트라이어드(V)
  • 6위 : 마이너 트라이어드 (vi)
  • 7위 : 삼합회 감소 (세부o)

제7화음성

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/1 <c e g b>1_\markup IM7 <d f a c>_\markup ii7 <e g b d>_\markup iii7 <f a c e>_\markup IVM7 <g b d f>_\markup V7 <a c e g>_\markup vi7 <b d f a>_\markup viiø7}}

각각의 음계도에 만들어진 일곱 번째 화음은 독특한 패턴을 따릅니다.로마 숫자 분석은 괄호 안에 나와 있습니다.

메이저 키와의 관계

악곡(또는 악곡의 일부)이 장음인 경우 해당 장음계의 음은 전음계로 간주되며 장음계 이외의 음은 반음계로 간주됩니다.또한, 음악(또는 섹션)의 주요 시그니처는 일반적으로 해당 장음계의 우연성을 반영합니다.

예를 들어 악곡이 E♭장조인 경우에는 E♭장조의 7개 피치(E♭, F, G, A♭, B♭, C, D)를 디오토닉 피치로 하고, 나머지 5개 피치(E♭, F/G♭, A/G♭, B♭, C/D)를 디오토닉 피치로 한다.이 경우 키 서명은 세 개의 플랫(B♭, E♭ 및 A♭)을 가집니다.

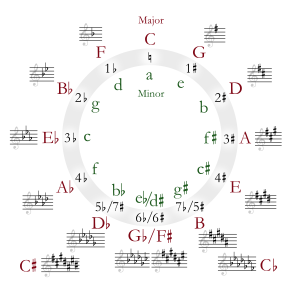
다음 그림은 12개의 상대적인 메이저키와 마이너키를 모두 나타내고 있으며, 외부에는 메이저키가, 내부에는 마이너키가 5분의 1의 원 주위에 배치되어 있습니다.

동그라미 안의 숫자는 키 시그니처의 샤프 또는 플랫의 수를 나타냅니다.샤프 키는 시계방향으로, 플랫 키는 C장조(샤프 또는 플랫이 없음)에서 시계반대방향으로 이동합니다.원형 배열은 원의 엔히모닉 관계에 따라 달라지며, 일반적으로 F shar = G=의 주 키의 경우 6개의 [3]샤프 또는 플랫으로 계산되며, 단조 키의 경우 D♭ = E♭로 계산된다.7개의 샤프 또는 플랫은 5개의 플랫 또는 샤프(D♭메이저 또는 B메이저)와 함께 철자가 더 편리할 수 있는 메이저 키(C+장조 또는 C♭메이저)를 만든다.

넓은 의미

"장음계"라는 용어는 또한 1도, 3도, 5도가 3도인 다른 음계의 이름에서도 사용된다.

고조파 장음계는[4][5] 마이너 6을 가진다.3도만 높이면 고조파 단음계와 다릅니다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { Harmonic major scale } d e f g aes b c } }

멜로디 장음계라는 이름으로 불리는 두 가지 음계가 있습니다.

첫 번째는 재즈 마이너[citation needed] 스케일의 5번째 모드이며, 6도, 7도가 내려간 메이저 스케일(아이오니아 모드) 또는 3도가 올라간 자연 마이너 스케일의 자연 마이너 스케일(어올리언 모드)이라고 할 수 있다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { Melodic major scale } d e f g aes bes c } }

두 번째는 이오니아 오름차순과 이전의 멜로디 장조 오름차순을 합친 음계입니다.3단계가 [6]3단조로 올라가는 것만으로 멜로디 단음계와 다르다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { Melodic major (ascending and descending) } d e f g a b c bes aes g f e d c } }

이중 고조파 장음계에는[7] 단초와 단초 6이 있습니다.헝가리 단음계의 다섯 번째 모드입니다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 7/4 c4^\markup { Double harmonic major scale } des e f g aes b c } }

「 」를 참조해 주세요.

레퍼런스

  1. ^ Benward, Bruce & Saker, Marilyn(2003).음악: 이론과 실천, Vol. I, 페이지 52제7판 ISBN978-0-07-294262-0.
  2. ^ "Major scale music".
  3. ^ Drabkin, William (2001). "Circle of Fifths". In Sadie, Stanley; Tyrrell, John (eds.). The New Grove Dictionary of Music and Musicians (2nd ed.). London: Macmillan Publishers.
  4. ^ Rimsky-Korsakov, Nikolai (2005). Practical Manual of Harmony. Carl Fischer, LLC. ISBN 978-0-8258-5699-0.
  5. ^ Tymoczko, Dmitri (2011). "Chapter 4". A Geometry of Music. New York: Oxford.
  6. ^ "Archived copy". Archived from the original on 2014-03-11. Retrieved 2014-03-13.{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크)
  7. ^ Stetina, Troy (1999). The Ultimate Scale Book. p. 59. ISBN 0-7935-9788-9.

추가 정보

외부 링크