양자 난소성

에 관한 일련의 기사의 일부
양자역학
${\displaystyle i\hbar {\frac t} \psi (t) \rangle = {H} \psi (t) \rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전 역학 구 양자론 브라켓 표기법 해밀턴식 방해다
기초 상보성 데코히렌스 얽힘 에너지 레벨 측정. 비국소성 양자수 주 중첩 대칭 터널링 불확실성 파동 함수 접다
실험 벨 부등식 데이비슨-게르머 더블 슬릿 엘리추르-바이드만 프랑크-헤르츠 레깃-가르그 부등식 마흐-젠더 포퍼 양자 지우개 선택 지연 슈뢰딩거의 고양이 스턴-게라크 휠러의 지연 선택
제제 개요 하이젠베르크 상호 작용 매트릭스 위상 공간 슈뢰딩거 Sum-over-History(경로 적분)
방정식 디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석 개요 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션
상세 토픽 상대론적 양자역학 양자장론 양자정보과학 양자 컴퓨팅 양자 카오스 밀도 매트릭스 산란 이론 양자통계역학 양자 기계 학습
과학자 아하로노프 벨 베테 블래킷 블로치 쾅 보어 태어난 보스 드 브로글리 콤프턴 디락 데이비슨 데비 에렌페스트 아인슈타인 에버렛 폭 페르미 파인만 글라우버 거츠빌러 하이젠베르크 힐베르트 조던 크래머스 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 온네스 플랑크 라비 라만 리드버그 슈뢰딩거 시몬스 솜메르펠트 폰 노이만 와일 빈 위그너 지만 자이링거
v t

이론물리학에서 양자비국위성은 다분할 양자시스템의 측정통계가 국소실재론의 관점에서 해석을 허용하지 않는 현상을 말한다.양자 비대위성은 다른 물리적 ^{[1][2][3][4][5]}가정 하에서 실험적으로 검증되었다.양자 이론을 대체하거나 대체하는 것을 목표로 하는 물리 이론은 그러한 실험을 설명해야 하며, 따라서 국지적 사실주의를 이행할 수 없다; 양자적 비대위성은 자연에 대한 우리의 설명과 독립적인 우주의 속성이다.

양자 비대위성은 빛보다 빠른 ^[6]통신을 허용하지 않기 때문에 특수 상대성 이론과 물체의 보편적 속도 제한과 양립할 수 있다.따라서 양자이론은 특수상대성이론에 의해 정의된 엄밀한 의미에서 국소적이며, 따라서 "양자 논로컬리티"라는 용어는 때때로 잘못된 명칭으로 여겨진다.그럼에도 불구하고, 그것은 양자 이론에 관한 많은 근본적인 논의를 촉발시킨다.

역사

아인슈타인, 포돌스키, 로젠

1935년 아인슈타인, 포돌스키, 로젠은 그들이 ^[7]묘사한 미시적 규모의 국소적 인과관계 위반과 관련하여 코펜하겐의 양자역학 해석의 불완전성을 드러내고자 하는 사고 실험을 발표했다.그 후 아인슈타인은 에르빈 ^[8]슈뢰딩거에게 보낸 편지에서 이 아이디어의 변형을 제시했는데, 이것이 여기에 제시된 버전이다.여기서 사용되는 상태와 표기법은 좀 더 현대적이며, EPR에 ^[9]대한 David Bohm의 견해와 유사합니다.측정 전 두 입자의 양자 상태는 다음과 같이 기록될 수 있습니다.

${\displaystyle \left \psi _{AB}\right\rangle = specfrac {1}{\bigg (}\left 0\right\rangle _{A}\left 1\right\rangle _{B}-\left 1\right 0\rangle _{B}-rangle _{A}\rangle }$

여기서${\displaystyle }$± ${\displaystyle ⟩}$ ${\displaystyle =}$ ${\displaystyle 1\frac{\mathrm{}}{}\frac{\sqrt{2\mathrm{}}}{}}$ ( ${\displaystyle 0\mathrm{}⟩}$ ± ${\displaystyle 1\mathrm{}}$) $){$ $displaystyle \ left$ \$pm \right$ \rangle =$specfrac {1}{\right$rt {$2}\left$(\$left$ 0$\right \pm \left$ 1$\right$\rangle \$right$ )$}$^[10]

여기서 첨자 "A"와 "B"는 두 입자를 구별합니다. 그러나 이러한 입자를 앨리스와 밥이라고 불리는 두 실험자가 소유하고 있는 것으로 언급하는 것이 더 편리하고 일반적입니다.양자 이론의 법칙은 실험자들이 수행한 측정의 결과에 대한 예측을 제공한다.예를 들어 앨리스는 평균 50%의 측정값으로 회전하는 입자를 측정합니다.단, 코펜하겐 해석에 따르면 Alice의 측정은 두 입자의 상태를 붕괴시키기 때문에 Alice가 z방향으로 스핀 측정을 수행하는 경우$,{\displaystyle }$ 즉 ${\displaystyle {기준\mathrm{}}_{}}$ {${\displaystyle {}_{}}$ A, ${\displaystyle {1\mathrm{}}_{}}$ A$$ {\$displaystyle \{\left$ 0$\right \rangle$ _${A},$ \$left$ 1$\right {A$ {\rangle _RANG}}에 대해 실행됩니다.의 시스템은 {${\displaystyle {0\mathrm{}}_{}}$ B${\displaystyle {}_{}}$}${\displaystyle }$、 ${\displaystyle {1\mathrm{}}_{}}$ B$}$ { $displaystyle$ \ { \$left$0 \ $right$\$rangle _$ { $B$}$$} 。또한 Alice가 x방향으로 스핀을 측정하는 경우$,{\displaystyle }$ 즉 ${\displaystyle {}_{}}$ ${\displaystyle {\{}_{}}$ + ${\displaystyle {\}}_{}}$ - $}$ft $-$ $\ right$ \ $rangle$_ { $A$} \$$${\displaystyle {\}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {、}_{}}$ B$}$（ \ $display$ \ { \ $style$ \ { \$left$ + \$right$ \ $rangle$_ { $B }$）${\displaystyle }$。슈뢰딩거는 이 현상을 "스티어링"^[11]이라고 부릅니다.이 스티어링은 이러한 상태 업데이트를 수행하여 신호를 보낼 수 없는 방식으로 발생합니다. 양자 비국소성은 메시지를 즉시 보내는 데 사용할 수 없으므로 특수 상대성 ^[10]이론의 인과 관계 우려와 직접적으로 충돌하지 않습니다.

이 실험의 코펜하겐 관점에 따르면 앨리스의 측정, 특히 앨리스의 측정 선택은 밥의 상태에 직접적인 영향을 미칩니다.단, 지역성이라는 가정 하에 앨리스의 시스템에서의 동작은 밥의 시스템의 "진짜" 또는 "독성" 상태에 영향을 주지 않습니다.Alice가 양자 상태 중 하나로 결론을 내릴 수 있기 때문에 Bob 시스템의 온틱 상태는 양자 상태 ${\displaystyle {\uparrow }_{}}$ $(\$\left $\uparrow \right \rangle$ _${B})$ 또는$$ ${\displaystyle {\downarrow }_{}}$ $(\$ _${B$ 중 하나와 호환되어야 합니다.그의 시스템의.동시에 양자 상태 ${\displaystyle {\leftarrow }_{}}$ ${\displaystyle {}_{}}$ \ $displaystyle \$left \ $arrow \ right$ \ $rangle$_ { $B$} 또는$$ $display$ B \ $displaystyle$ \$left \ right$ \ $rangle$ _ { B$$} 중$$ 하나와 호환성이 있어야 합니다.따라서 밥의 시스템의 온전한 상태는 적어도 두 개의 양자 상태와 양립할 수 있어야 한다. 따라서 양자 상태는 그의 시스템을 완전히 설명하는 것이 아니다.아인슈타인, 포돌스키, 로젠은 파동 함수가 이 국소적인 가정하에서 양자 시스템에 대한 완전한 설명이 아니기 때문에 양자 이론의 코펜하겐 해석의 불완전성의 증거로 보았다.그들의 논문은 다음과 같이 결론:^[7]

따라서 우리는 파동 함수가 물리적 현실에 대한 완전한 설명을 제공하지 않는다는 것을 보여주었지만, 그러한 설명이 존재하는지 여부에 대한 질문은 열어두었다.그러나 우리는 그러한 이론이 가능하다고 믿는다.

다양한 저자들(특히 닐스 보어)이 EPR ^[12][13]논문의 애매한 용어를 비판했지만, 그럼에도 불구하고 사고 실험은 많은 관심을 불러일으켰다."완전한 설명"에 대한 그들의 개념은 나중에 측정 결과의 통계를 결정하지만 관찰자가 접근할 ^[14]수 없는 숨겨진 변수의 제안으로 공식화되었다.보미안 역학은 숨겨진 변수의 도입과 함께 양자 역학의 완성도를 제공합니다; 그러나 이론은 명백하게 ^[15]국부적이지 않습니다.따라서 이 해석은 양자역학의 완전한 ^[16]설명이 "국소 작용의 원리"에 부합하는 지역적 숨겨진 변수들의 관점에서 주어질 수 있는지 여부에 대한 아인슈타인의 질문에 대한 답을 주지 못한다.

벨 부등식

1964년 존 벨은 아인슈타인의 질문에 그러한 국지적인 숨겨진 변수들이 ^[17]양자이론에 의해 예측된 모든 범위의 통계적 결과들을 재현할 수 없다는 것을 보여주면서 대답했다.Bell은 국소 숨은 변수 가설이 측정 결과의 상관 관계에 대한 제한으로 이어진다는 것을 보여주었다.양자역학에 의해 예측된 대로 벨 부등식이 실험적으로 침해된다면, 현실은 국지적인 숨겨진 변수로 묘사될 수 없고 양자 비국지적 인과관계에 대한 미스터리는 남는다.Bell에 ^[17]따르면:

이 [극히 국소적이지 않은 구조]는 양자역학적 예측을 정확하게 재현하는 모든 이론의 특징입니다.

Clauser, Horne, Shimony 및 Holt(CHSH)는 실험 테스트에 더 도움이 되는 방식으로 이러한 불평등을 재구성했다(CHSH ^[18]불평등 참조).

벨이 제안한 시나리오(벨 시나리오)에서는 앨리스와 밥이라는 두 실험자가 별도의 실험실에서 실험을 수행합니다.앨리스(Bob)는 매번 $실험실$에서 x$($$)\$$displaystyle$(y)\$displaystyle(y)\$displaystyle a$($$)\displaystyle(b$displaystyle(b)\displaystyle(b)\style(a, b)\$displaystyle$(yle)\style) $실험$을 여러 번 반복하면 $확률{\displaystyle }$P(${\displaystyle a,}$ ${\displaystyle b,}$ $)$를 추정할 수 있습니다.$P(a,$b x$, y$ 즉 Alice와 Bob이 각각 x, y 실험을 수행할 때 a${\displaystyle ,}$ $(\displaystyle$ a,$b)$ $결과$를 관찰할 확률.다음 각 확률${\displaystyle \mathrm{세트}}${${\displaystyle }$P (${\displaystyle a}$ , ${\displaystyle b}$x ,${\displaystyle y}$) :${\displaystyle }$a ,${\displaystyle b}$ ,${\displaystyle x}$ , ${\displaystyle y}$ { $displaystyle$$$\ { P $( a$ , ${\displaystyle b}$$x$ ,$y$ ) : $a$, ${\displaystyle b}$$$, ${\displaystyle x}$$$, $y$$}$$non$ non 、 non $nonality$ $non{\displaystyle }$、 P (${\displaystyle }$${\displaystyle a}$$$, b ,$x$, y )$$。

Bell은 각 $시스템$의 ^[17]측정 결과를 로컬로 특징짓기 위해 파라미터$${\(\$displaystyle\lambda)$를 도입함으로써 숨겨진 변수의 개념을 공식화했습니다. "이것은 무관심의 문제입니다.θ가 단일 변수인지 집합인지 그리고 변수가 이산형인지 연속형인지.$그러나{\displaystyle }$ Alice와 Bob이 실험 셋업을 재부팅했을 때 ${\displaystyle \{\backslash }$ ( ${\displaystyle )}$ $)\displaystyle \rho$( \$lambda$)가$$$$ $발생$할 가능성이 있는 로컬 "전략" 또는 "${\displaystyle \mathrm{메시지}}$"라고 생각하는 것은 동등하고 직관적입니다.EPR의 로컬 분리 가능성 기준은 Alice가 x 실험을 수행하고 $Bob이$ 실험을 $수행$하는 경우 각 로컬 전략이 독립적인 결과의 분포를 정의하도록 규정한다$.$

$여기$서 ${\displaystyle {PA}_{}x,}$ $)$ {$displaystyle P_{A}(a,\lambda_{A})$ $$(${\displaystyle {PB}_{}b}$ y${\displaystyle ,}$ ${\displaystyle b_{}}$B$)$ {$displaystyle$ $P_{B}(b$ y$,\lambda_{B$는 Alice$(by$,\lambda_{B$\})$${\displaystyle }$가 결과를 얻을 확률을 나타냅니다$.$${\displaystyle (}$ ${\displaystyle y}$)$${$displaystyle ( y$ ) the$$ the the the the describ describ describ describ ${\displaystyle {describ}_{}}$ A$$\ $displaystyle$\ $lambda$_ { $A$}$$ （ ${\displaystyle B_{}}$\ $displaystyle$\$lambda$ _ {$B$}$$ ） 。

${\displaystyle {}_{}{}_{}}$ $(\$ _${A},\lambda$ _${B})$가 일부 세트$\lambda {\displaystyle \mathrm{}}$(\$displaystyle$$$\$lambda$ _$\{$B})에서 값을 가져올 수 있다고 가정합니다.${\displaystyle {각}_{}}$ 값의 ${\displaystyle {쌍}_{}}$이 A${\displaystyle {}_{}}$ ${\displaystyle \mathrm{B}}$,$$ \$displaystyle$ \$lambda$_{$A},$ \lambda }인$$${\displaystyle {}_{}{}_{}}$ 경우, \lambda$}$_lamda {\$lam$}, \lamda}의 값을 $가져옵니다$.$선택된 람다$ _${B}}($예$$: ${\displaystyle a_{}}$A , ${\displaystyle b_{}}$B \ $displaystyle \lambda$ _${A}$ ,\$lambda$ _${B}$ )의$$ 경우, 이 분포에 대한 평균을 구하여 각 측정 결과의 결합 확률에 대한 공식을 구할 수 있습니다.

이러한 분해를 허용하는 상자를 Bell local 또는 classical box라고 합니다.a${\displaystyle ,}$ ${\displaystyle b,}$ ${\displaystyle x,}$ $(\displaystyle$ a,$b, x, y$)가 각각 취할 수 있는 값의 수를 고정하면 각 $상자{\displaystyle }$ P${\displaystyle (a,}$ b${\displaystyle x}$, $)$ (\$displaystyle$ P$(a,$b ${\displaystyle {x,}_{}}$$y$${\displaystyle {))}_{}}$를 엔트리${\displaystyle {}_{}}$P${\displaystyle {(a,}_{}}$ ${\displaystyle b_{}}$ x, ${\displaystyle {y),}_{}}$ a${\displaystyle {,}_{}}$ $,$ $, y($의 유한 벡터로 나타낼 수 있습니다., 모든 고전적인 상자의 집합은 볼록한 폴리토프를 형성합니다.CHSH에 의해 연구된 $Bell{\displaystyle \mathrm{시나리오}}$에서는$,$ $,$ x, y(\$displaystyle a, b,$ x, y$$${\displaystyle )}$는$$0,$$1(\$displaystyle$ {0$,$1$\})$ $내$의 값을 가질 수 있으며, 모든 Bell $로컬박스{\displaystyle }$ P$(a, b, y)$는 CHSH 부등식을 충족해야 합니다.

어디에

위의 고려사항은 양자 실험 모델에 적용됩니다.초당 광자 상태에서 국소 편광 측정을 수행하는 두 당사자를 고려합니다.광자의 편광에 대한 측정 결과는 두 값 중 하나를 취할 수 있다(비공식적으로 광자가 그 방향으로 편광되는지 직교 방향으로 편광되는지 여부).각 당사자가 2개의 서로 다른 편광 방향 중 하나를 선택할 수 있는 경우 실험은 CHSH 시나리오에 들어맞습니다.CHSH에 기재된 바와 같이 양자상태와 편광방향이 존재하며, ${\displaystyle {S\mathrm{}}_{}}$ ${\displaystyle {\mathrm{C}}_{}}$ ${\displaystyle {\mathrm{H}}_{}}$H H {\$displaystyle S_{\rm {CHSH}}$가 ${\displaystyle 2⁄2.828}${\$displaystyle$ 2$\qrt}$인 박스$(a, b$가 생성됩니다.국소적이고 국소적인 측정과 국소적인 작용만이 양자 이론의 확률론적 예측과 일치할 수 없는 논리적 상태, 아인슈타인의 가설을 반증한다.알랭 애스펙트와 같은 실험론자들은 벨의 부등식의 다른 공식뿐만 아니라 CHSH 부등식의 양자 위반을 검증하여 국지적인 숨겨진 변수 가설을 무효화하고 EPR의 의미에서 현실이 국지적이지 않음을 확인하였다.

가능성론적 논로컬리티

벨에 의한 국소성의 증명은 양자역학에 의해 예측된 정확한 확률을 국소이론에 의해 충족시킬 수 없다는 점에서 확률론적이다.(간단히 "국소이론"은 "국소 숨은 변수 이론"을 의미한다.)그러나 양자역학은 국지적인 이론의 훨씬 더 강력한 위반을 허용한다: 국지적인 이론이 얽힌 시나리오에서 어떤 사건이 가능하거나 불가능한지에 대해 양자역학과조차 일치하지 않는 가능성론이다.이러한 종류의 첫 번째 증거는 1993년^[20] Greenberger, Horne, Zeilinger에 의해 있었습니다. 관련된 주는 종종 GHZ 상태로 불립니다.

1993년, 루시엔 하디는 GHZ 증명처럼 양자 논국적성의 논리적 증거를 ^[21][22][23]증명했다.먼저 아래에 정의된 상태 $(\$})를$$ 몇 가지 시사적인 방법으로 기술할 수 있습니다.

$(\displaystyle \left \psi \right\rangle = specfrac {1} {\right {3}\left (\left 00\right\rangle +\left 01\right\rangle +\left 10\right\rangle +\right) = spec frac {1} {\left\right {\right}각도 +{\frac {1}{\fracrt {2}}\left(\left 1+\right\rangle +\left 1-right\rangle \right)\right)}$

여기서 ± ${\displaystyle ⟩}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle =\frac{}{}\frac{\sqrt{1\mathrm{}}}{}}$ ${\displaystyle 2\mathrm{}}$ ( 0${\displaystyle 1\mathrm{}}$ ± 1$)$ $){ displaystyle \pm$ \rangle =$fr tfrac${1}{\$suptrt {$2$}$ $（ left$0 \$right 1$ \ $right$ \ $rangle$） $\}$${\displaystyle }$。

실험은 두 실험자가 공유하는 이 얽힌 상태로 구성됩니다.각 실험자는 기본 {$0$ 1${\displaystyle }$⟩$\},{\displaystyle }$ ${\displaystyle$ \{\left 0$\right\rangle,\left$ 1$\right\rangle$\} 또는$$${\displaystyle }${ +$$ -$}$ {\$displaystyle \{\$$left$ \right \$right$ \$rangle\$rangle$\$rangle }}에 $대해$ 측정할 수 있습니다.$$. ${\displaystyle 각각\mathrm{}}$ {0 ${\displaystyle ,}$ 、 ${\displaystyle 1\mathrm{}}$⟩ $}$ { $displaystyle$\ { \$left$0 \ $right$ \ $rangle$} , \ $left$$1$$$\$$$right$ \ $rangle$ ${\$ with ${\displaystyle with\mathrm{}}$ 、 { $0$$$ 、 ${\displaystyle 1\mathrm{}}$ $、 right$ \ rangle$$$}$⟩ $⟩{\displaystyle }$ ⟩ ${\displaystyle see\mathrm{}}$ see see see see see see see with with with with see see see the see with the with with with with the the the the the the with with with with$angle \}$ 및$$ 기타 { +${\displaystyle +}$ 、${\displaystyle }$-${\displaystyle }$display${\displaystyle }$${\displaystyle \}(\backslash }$$displaystyle$$$\{\$left +\right \rangle$ $,\backslash$left $-$${\displaystyle \backslash }$$right$$$$\$${\displaystyle rangle}$$$${\displaystyle \mathrm{}}$$$)의${\displaystyle }$결과는 표시되지 않습니다$.-$ 0 -$$0 - 0 - "$$${\displaystyle 。}$ 단, \$displaystyle$\$left$ $0$$$-$\$right \$rangle$${\displaystyle }$$.$$t$ $--\right\rangle }$ { +${\displaystyle \},}$- ${\displaystyle \}}${$displaystyle \{\left +\right\rangle,\left -\right\rangle$에${\displaystyle }$대해 측정하는 경우, ${\displaystyle ⟨}$ -${\displaystyle =}$ - ${\displaystyle \frac{1\mathrm{}}{}}$ ${\displaystyle \frac{2\sqrt{\mathrm{}}}{}}$ ${\displaystyle \frac{\ne }{}0}$. \ $display style -- \ psi$ \ $rangle$= - { $right$ \ rangle } { $right$\ $rangle$} { rangle } { rangle } { rangle } } { rangle } { rangle } } } } }

이것은 역설로 이어집니다. -${\$ { $displaystyle --$ \ $rangle$} $실험자$ 중 한 명이 { 0$$ , 1${\displaystyle 1\mathrm{}}{\displaystyle \}}$ { \$display style$ \ $right$\ rangle , \$left$ 1 \ right \ rangle$$ $\$ }$$instead instead ${\displaystyle instead\mathrm{}}$ instead instead instead with with with with with with with with with with with with with 、 1$$、 1 -1 -1 -1 $-1$ -1 -1 -1 -1 -1 -1 $-1$ ${\displaystyle -}$${\displaystyle e\mathrm{}}$$}$ ${\displaystyle 또는}$ 1 - 0$$- 0 ${\$ { $displaystyle${ - }$$0 \ rangle$$ $}$ ${\displaystyle 및\mathrm{}}$0 - 0 - $⟩$ { $displaystyle 0$- \ $rangle$$$$}$은${\displaystyle (}$는) 불가능합니다.단, 둘${\displaystyle 다\mathrm{}}$ {${\displaystyle 0\mathrm{}}$ ${\displaystyle ,}$ }, 1${\displaystyle }$⟩$}$ { $displaystyle$\ { \ $left 0$ \$right$ \ rangle }, \ $left$1 \$right$ \ rangle$$}에$$ 대해 측정했을 경우, 지역별로도 결과는 11$${\(\ $displaystyle$\ $left$ 11 $\ right$ \ $rangle$이어야 합니다.

전파 속도가 유한한 로컬 숨김 변수 모델

Bancal ^[24]et al.의 연구는 양자 이론에서 달성할 수 있는 상관관계가 또한 많은 종류의 초광속 숨겨진 변수 모델과 양립할 수 없다는 것을 증명함으로써 벨의 결과를 일반화한다.이 프레임워크에서는 빛보다 빠른 시그널링은 제외됩니다.단, 초광속적인 영향(유한하지만 그 외에는 알려지지 않은 속도)이 한 지점에서 다른 곳으로 전파될 수 있는 충분한 시간이 있는 경우, 한 당사자의 설정 선택은 다른 당사자의 먼 위치에 있는 숨겨진 변수에 영향을 미칠 수 있습니다.이 시나리오에서는 벨의 비국소성을 드러내는 모든 초당적 실험은 숨겨진 영향의 전파 속도에 대한 하한을 제공할 수 있다.그럼에도 불구하고, 세 명 이상의 당사자가 있는 양자 실험은 이러한 모든 비국소 숨겨진 변수 모델을 ^[24]반증할 수 있다.

보다 복잡한 인과 구조에서의 벨 정리 유사점

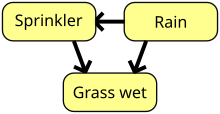
일반 실험에서 측정된 랜덤 변수는 서로 복잡한 방식으로 종속될 수 있습니다.인과 추론 분야에서, 그러한 의존성은 베이지안 네트워크를 통해 표현된다: 각 노드가 변수를 나타내며 변수에서 다른 노드로의 에지를 나타내는 방향 비순환 그래프는 전자가 후자에 영향을 미친다는 것을 나타내며, 그렇지 않은 경우에는 그림을 참조한다.표준 초당 벨 실험에서는 앨리스(Bob'$$s)의 $설정{\displaystyle }$ x$($$y)$와 로컬 변수 ${\displaystyle a_{}}$ A$(\$$\lambda$ _${A})$가 함께 로컬 $디스플레이$에 $영향$을 줍니다$(\displaystyle \$$lambda$$$_${B}).$$$$$따라서 벨의 정리는 하나의 숨겨진 노드$({\displaystyle }$ ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$ ${\displaystyle b_{}}$ B$)$를 가진 인과 구조의 유형에서 양자 예측과 고전 예측 사이의 분리로 해석될 수 있다.\$displaystyle (\lambda$_{$A},\lambda$_{$B$ 다른 유형의 인과 ^[25]구조에서도 유사한 분리가 확립되었다.이러한 확장 벨 시나리오에서 고전적 상관관계에 대한 경계를 특성화하는 것은 어렵지만,^[26][27] 이를 달성하기 위한 완전한 실용적인 계산 방법이 존재한다.

얽힘과 비장소성

양자 비대위성은 때때로 얽힘과 동등하다고 이해된다.그러나 이것은 사실이 아니다.양자 얽힘은 양자 역학의 형식주의 내에서만 정의될 수 있다. 즉, 모델에 의존하는 특성이다.이와는 대조적으로, 비국소성은 국소적인 숨겨진 변수 모델의 관점에서 관측된 통계를 설명하는 것이 불가능함을 의미하므로, 실험을 설명하는 데 사용되는 물리적 모델과 독립적이다.

순수하게 얽힌 상태에 대해 Bell 비국소 상관관계를 생성하는 측정의 선택지가 존재하는 것은 사실이지만 혼합 상태의 경우 상황은 더 복잡합니다.Bell 비로컬스테이트는 얽혀 있을 필요가 있지만, Bell 비로컬^[28] 상관관계를 생성하지 않는(혼합된) 스테이트가 존재합니다(다만, ^[29]이러한 스테이트의 몇개의 카피로 동작하거나 로컬의 포스트 ^[30]선택을 실행했을 경우, 로컬 이외의 효과를 볼 수 있습니다).게다가 ^[31]얽힘에는 촉매가 있지만, ^[32]비국소성에는 촉매가 없습니다.마지막으로, 가장 큰 위반을 주는 양자 상태가 절대 최대로 얽힌 상태가 아닌 벨 부등식의 합리적으로 단순한 예가 발견되었고, 얽힘은 어떤 의미에서는 비국소성에 ^[33][34][35]비례하지 않는다는 것을 보여준다.

양자 상관

그림과 같이, 고전적인 시스템에서 실험을 수행하는 둘 이상의 당사자가 달성할 수 있는 통계는 중요하지 않은 방법으로 제약된다.마찬가지로, 양자 이론에서 개별 관측자가 달성할 수 있는 통계도 제한된다.B로 인해 양자 상관 집합에 대한 사소한 통계적 한계의 첫 번째 파생입니다. 치렐슨,^[36] 치렐슨 바운드라고 알려져 있어요.앞에서 설명한 CHSH Bell 시나리오를 고려하지만 이번에는 Alice와 Bob이 양자 시스템을 준비하고 측정한다고 가정합니다.이 경우 CHSH 파라미터는 다음과 같이 제한됨을 나타낼 수 있습니다.

${\displaystyle -2{\sqrt {2}}\leq \mathrm {CHSH} \leq 2{\sqrt {2}}.}$

양자 상관관계와 시렐슨의 문제

수학적으로 $박스{\displaystyle }$ P${\displaystyle (a,}$ ${\displaystyle b}$x, $)$ {$displaystyle$ P$(a, b x, y$)}는$$ Hilbert $공간{\displaystyle {}_{}}$ $,$(\$displaystyle$ H_${A}, H_{B$ 정규화 벡터 $display$ ${\displaystyle {H\_Display}_{}}$가 존재하는 경우에만 양자 실현이 가능합니다${\displaystyle {}_{}}$$연산자{\displaystyle {}_{}^{}}$ ${\displaystyle E_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}{}_{}^{}}$: ${\displaystyle H_{}}$ A ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle A_{}}$、 ${\displaystyle F_{}^{}}$ ${\displaystyle {}_{}^{}}$y : ${\displaystyle H_{}}$ B ${\displaystyle {}_{}}$ ${\displaystyle H_{}}$B ( \ $displaystyle E_{a$}^{$x):$$H_{A}\to H_{A}, F_{b}^{y}:$$H_{B}\to$ H_${B}}$는 다음과 같습니다.

1. $모든{\displaystyle }$ x${\displaystyle ,}$ ${\displaystyle y}${\$displaystyle$ x$,y$에 대해 세트 $\{{\displaystyle E_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle a_{},}$ {${\displaystyle F_{}^{}}$ b ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle b_{}}$ ${{$\{$E_{a}^{x}\}_{a},\{F_{b}^{y}\}_{b}$는 완전한 측정을 나타냅니다.즉,${\displaystyle \underset{}{}{aa}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}^{}{}_{}{I}_{}}$ A${\displaystyle \underset{}{}}$ ${\displaystyle {bb}_{}^{}}$ F b ${\displaystyle {}_{}^{}}$ $=$ ${\displaystyle {\mathbb{}}_{}}$ $({displaystyle$ \$sum _{a}E_{a$}^{x}= $mathmathbb {I}_{A},\sum$_{$b}F_{y$}= $mathmathbbbb {I})_{$B$\}$이다.
2. ${\displaystyle }$$P{\displaystyle }$${\displaystyle }$( ${\displaystyle a}$, ${\displaystyle bx}$ ,${\displaystyle y}$ ) ${\displaystyle =}$${\displaystyle }$${\displaystyle {displaydisplayE}_{}^{}}$ a ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}^{}}$ b y ${\displaystyle displaydisplay{}_{}^{}}$ $、$ \ $display$ $style$$$P ($a$ , $b x$ , y ) = \$left$ \ $psi$\$right$ E _ { $a$}^{$x$${\displaystyle }$} \$otimes$ F _ { $y$$$$\}$ \ ${\displaystyle \mathrm{left}}$ $\$$psi$ \ $right$\$rangle$$。$

다음에서는 이러한 상자의 집합을 Q$(\displaystyle$ Q$)$라고 $부릅니다{\displaystyle }$. 기존의 상관 관계 집합과 달리 확률 공간에서 볼 때 Q$(\displaystyle$ Q$)$는 폴리토프가 아닙니다.반대로 직선 ^[37]경계와 곡선 경계를 모두 포함하고 있습니다.또한 Q$(\$$displaystyle$ Q$)$는 닫혀 ^[38]있지 않습니다.이는 양자 시스템에 의해 임의로 근사할 수 있지만 양자 자체는 아닌 $상자{\displaystyle }$ P$(a, b$x,$y)$가 존재함을 의미합니다.

위의 정의에서 벨 실험을 수행하는 두 당사자의 공간 같은 분리는 연관된 연산자 대수가 전체 힐베르트 $공간{\displaystyle }$ H ${\displaystyle =}$ ${\displaystyle H_{}}$ = ${\displaystyle {}_{}}$⊗ H B $디스플레이$H =$H$= H _ { ${\displaystyle A_{}}$$$${\displaystyle {}_{}}$의 $다른 요인$ H ${\displaystyle A_{}}$ , $B 에$ 작용하도록 하여 모델링되었다.실험.대안으로, 이 두 대수가 통근하도록 함으로써 우주와 같은 분리를 모델링할 수 있다.그러면 다음과 같은 정의가 달라집니다.

${\displaystyle P}$( ${\displaystyle a}$, ${\displaystyle bx}$ ,${\displaystyle y}$ $){$ $displaystyle$P ($a$ , $b x$ ,$y$ ){ $displaystyle$ H$\}$는 정규화$$ 벡터 ${\displaystyle \psi }$ψ ${\displaystyle H}${ $displaystyle \$ psi \ $right \rangle$\ $in$H } 및$$ 투영 $연산자{\displaystyle {}_{}^{}}$ ${\displaystyle E_{}^{}}$ : A ${\displaystyle x{}_{}^{}}$H${\displaystyle {}_{}^{}\to }$ ${\displaystyle F}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$하는 경우에만 필드 양자 실현을 허용한다.$H\to H,F_{b}^{y}:$$그렇게 H\to$ H$\$to$$ H\toH

1. $모든{\displaystyle }$ x${\displaystyle ,}$ ${\displaystyle y}${\$displaystyle$ x$,y$에 대해 세트 $\{{\displaystyle E_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle a_{},}$ {${\displaystyle F_{}^{}}$ b ${\displaystyle {}_{}^{}{}_{}}$ ${\displaystyle b_{}}$ ${{$\{$E_{a}^{x}\}_{a},\{F_{b}^{y}\}_{b}$는 완전한 측정을 나타냅니다.즉,${\displaystyle \underset{}{}{\beta }_{}^{}}$ a ${\displaystyle {}_{}^{}}$ $=$,${\displaystyle \underset{\beta }{}}$ ${\displaystyle \underset{}{}{}_{}^{}}$ ${\displaystyle {}_{}^{}}$ y $=$ ${\displaystyle I\mathbb{}}${\$displaystyle \sum$ _${a}E_{a$}^{$x}={sum mathbb$ {I}},\$sum$ _{$b}F_{y$}=$mathbb {I}}}}}$이다$.$
2. ${\displaystyle }$$P$${\displaystyle }$( ${\displaystyle a}$, ${\displaystyle b}$x ,${\displaystyle }$y ) ${\displaystyle =}$${\displaystyle \mathrm{displaydisplayE}}$ ${\displaystyle {}_{}^{}}$ x ${\displaystyle F_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle displaydisplay{}_{}^{}}$displaydisplay$$displaydisplay $display$ 、 \ $display$ $style$$$P ($a$ , $b x$ , $y$ ) = \ $left$\$psi$\ $right$ E _ { $a$}^{ $x$$$} $F$_ { $b }$ \ right \$psi$\$rangle$$$、 $y$$。$
3. $displaystyle [E_{a}^{x}$$F_{b}^{y}=0$$모든{\displaystyle }$ a${\displaystyle ,}$ ${\displaystyle b,}$ ${\displaystyle x,}$ $\displaystyle$ a,$b, x, y$displaystyle a, y\)에 대해).

${\displaystyle Q_{}}$ c$${ $displaystyle$ Q _ { $c$} call$$ 、${\displaystyle }correl{\displaystyle }$ ${\displaystyle \mathrm{correl}}$ correl correl pP${\displaystyle }$( a ,${\displaystyle b}$ ${\displaystyle x}$,$$y ){ $displaystyle P$( a ,$b x$, y )$$} 를 호출합니다.

이 새로운 세트는 위에서 정의한 보다 $일반적$인$$Q(\$displaystyle$ Q$)$와 어떻게 관련되어 있습니까?${\displaystyle Q_{}}$c { $display Q$_ { $c$} closed$$ $closed{\displaystyle {}_{}}$ 。게다가, Q}\subseteq Q_{c}}, Q¯{\displaystyle{\bar{Q}}}Q{Q\displaystyle}의 폐쇄를 의미한다. Tsirelson의 problem[39]로 이루어져 있는지 여부 Q⊆ Qc{\displaystyle{\bar{Q}¯의 포함 관계}\subseteq Q_{c}}, 즉, whe엄격한 것인지 결정에⊆ Qc{\displaystyle{\bar{Q}¯.그r 또는 $not{\displaystyle \stackrel{}{}}$ Q ${\displaystyle =}$ ${\displaystyle Q_{}}$c { $displaystyle${$$Q$$}$$=$Q$_ { $c$} 。이 문제는 무한 차원에서만 발생합니다.${\displaystyle Q_{}}$ c$${ $displaystyle$ Q _ { $c$} $の$ Hilbert $space{\displaystyle }$ H$$（ \ $displaystyle$ Q _ { c } ） $this---{\displaystyle \stackrel{}{}}$ equals equals equals equals equals equals this this this this this this this this this this this h h h H { \ $displaystyle${$Q }$^[39]$）$ ${\displaystyle \stackrel{}{。}}$

2020년 1월, Ji, Natarajan, Vidick, Wright 및 Yuen은 양자 복잡도^[40] 이론의 결과를 ${\displaystyle {주장}_{}}$했는데$,$ 이는 Q${\displaystyle }$c c c c cr ({$displaystyle {Q}}\neQ Q_{c$를 암시하는 것으로 치렐슨의 ^{[41][42][43][44][45][46][47]}문제를 해결한 것이다.

치렐슨의 문제는 연산자 대수의 이론에서 유명한 추측인 코네스의 ^[48][49][50]삽입 문제와 동등하다는 것을 보여줄 수 있다.

양자 상관의 특성화

$(\$와 $(\$$displaystyle$ $H_{B})$의 치수는 원칙적으로 무제한이기 때문에 특정$a,$ y$)$의 양자 실현 여부를 판단하는 것은 복잡한 문제입니다.사실 양자상자가 로컬이 아닌 게임에서 만점을 받을 수 있는지 여부를 결정하는 이중 문제는 ^[38]판가름할 수 없는 것으로 알려져 있다.또한 P${\displaystyle (a,}$ ${\displaystyle b}$ x${\displaystyle ,}$ $)$ {$displaystyle$ P$(a, b$x, $y)}$가 $정밀도{\displaystyle \mathrm{}}$1/${\displaystyle \mathrm{poly}}$θ(${\displaystyle X}$Y$)$ {$displaystyle$ 1$/\operatorname {poly}(X$ Y$)}$의 양자계로 근사할 수 있는지 $여부$를 결정하는 ^[51]문제는 NP-hard이다.양자 박스를 특징짓는 것은 선형 제약 ^[52]조건 하에서 완전히 양의 반정의 행렬의 원뿔을 특징짓는 것과 같다.

작은 고정 $치수{\displaystyle {}_{}}$ ${\displaystyle {dA}_{}}$ $({$의 경우${\displaystyle ,}$ P(${\displaystyle a_{}}$, b${\displaystyle x}$,$)({displaystyle$ P$(a,$b$x,y$$)})$가 초당 양자 $시스템{\displaystyle {}_{}}$ HA${\displaystyle {}_{}{}_{}}$ ${B}$에서 실현될 수 있는지 $여부$를 변분법을 사용하여 탐색할 수 있다.$le \dim(H_{A})=d_{$${\displaystyle A}$$\}\},$ dim ${\displaystyle (}$ ( ${\displaystyle {HB}_{}}$) ${\displaystyle =}$ ${\displaystyle {dB}_{}}$ $($ \$displaystyle \dim$ ( $H_${$B$$}$=$d_{B$ ). 단, 이 방법은 P$$($a ,$ ,$y )$의 실현가능성을 증명하기 위해 사용할 수 있으며 양자시스템에서는 실현가능성이 아니다$.$

비현실성을 증명하기 위해 가장 잘 알려진 방법은 Navascués-Pironio-입니다.Acin(NPA) 계층.^[53]이것은 $상관관계{\displaystyle {}^{}}$ ${\displaystyle {세트}^{}}$의 무한감소 ${\displaystyle {시퀀스}^{}}$입니다.${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$ of${\displaystyle }$Q 2${\displaystyle {}^{}}$、 Q 3${\displaystyle }$. .$$\ $displaystyle$ Q^ { $1$ \ $supset$ Q^ { 2$$} \ $supset$ Q^ { $3$} \ $supset ...$} 속성$$$:$

1. $P$${\displaystyle }$(${\displaystyle a}$ , ${\displaystyle b}$x ,${\displaystyle y}$ )${\displaystyle {}_{}}$ Q$c ( a$ , $b x$ ,$y$ )\ $in$ Q _ { $c$} 、${\displaystyle }P{\displaystyle }$(${\displaystyle a}$ , b${\displaystyle x}$ ,${\displaystyle y}$ ) q ${\displaystyle Q^{}}$k ( $a$, $b$$x$ , y$)\ in Q^$ {$k$$$}$$${\displaystyle {}^{}}$ ${\displaystyle 。}$
2. ${\displaystyle P}$(${\displaystyle }$a , ${\displaystyle b}$x ,${\displaystyle y}$ )${\displaystyle }$q ${\displaystyle {}_{}}$ ($a$ , $b$x , $y$)\ $in Q$_ { $c$}\$$$display style$$$P ( ${\displaystyle a}$, ${\displaystyle b}$ x${\displaystyle }$, ${\displaystyle y)\notin }$ Q$$ ( a , b , y )\ $displaystyle$ P $( a$ ,$x$ , y )\$not$\ $in$Q$^$ { k$$$\}\}$ 가 ${\displaystyle {}^{}}$합니다.
3. 임의의$k{\displaystyle }$(\$displaystyle$ k$)$에 대해 P${\displaystyle (a,}$ b${\displaystyle x}$, ${\displaystyle y){}^{}}$ Q$$(\$display$ P$(a,$b x$,y)\in$ Q$^{k})$를 반확정 프로그램으로 캐스팅할 수 있는지 $여부$를 결정합니다.

따라서 NPA 계층은 Q$({displaystyle$Q$\})$가 아니라 Q$({$${$c$\})$의 연산 특성을 제공합니다. 치렐슨의 문제가 Q$= Q({$로 해결된다면 위의 두 가지 방법은 실용적인 특성을 제공할 수 있습니다.$(\$ 반대로 Q$(\$가 아닌 $Q(\$displaystyle {Q$})$의 경우 $(\$ {Q_${c}-{$의 상관관계를 검출하는 새로운 방법이 필요합니다.

초양자 상관의 물리학

위의 연구는 양자 집합의 상관관계를 설명하지만 그 이유를 설명하지는 않습니다.양자상관관계는 피할 수 없는 것일까, 양자상관후 물리이론에서도 피할 수 없는 것일까, 아니면 반대로 Q$(\$ $밖$에는 어떠한 비물리적 동작도 초래하지 않는 상관관계가 존재할 수 있는가?

포페스쿠와 로를리히는 1994년 논문에서 양자 상관관계가 상대론적 인과관계에만 ^[54]호소함으로써 설명될 수 있는지 여부를 탐구했다.즉, 가상의 $상자{\displaystyle }$ P$a$ ${\displaystyle b}$ x${\displaystyle ,}$ ${\displaystyle y)q\stackrel{}{}}$ Q ${\$ \ $displaystyle$ P$(a,$b x,$y)\ in$ \ $bar {Q$})\ in \ bar {Q$}\$ in \ bar {Q}\ would$$ \ would \ displaystyle P(a, b x, y)\ ${\$ \ displaysty\ in \ disposside style any any any any any any any any any any any두 당사자 사이의 상관 관계 수준에서 아인슈타인의 인과관계는 앨리스의 측정 선택이 밥의 통계에 영향을 미치지 않아야 한다는 요구로 해석됩니다. 그리고 그 반대도 마찬가지입니다.그렇지 않으면 앨리스(Bob)가 측정 $설정{\displaystyle }$ x$\displaystyle$ x$\backslash$${\displaystyle }$displaystyle($)\displaystyle(y)$을 적절하게 선택하여 밥(Alice)에게 즉시 신호를 보낼 수 있습니다.수학적으로 포페스쿠와 로를리히의 무신호 조건은 다음과 같다.

$\displaystyle \sum _{a}P(a,b x,y)=\sum _{a}P(a,b x^{\prime },y)=:P_{B}(b y),}$

$\displaystyle \sum _{b}P(a,b x,y)=\sum _{b}P(a,b x,y^{\prime })=:P_{A}(a x)}$

고전적인 상자 집합과 마찬가지로 확률 공간에서 표현될 때 무신호 상자 집합은 폴리토프를 형성합니다.Popescu와 Rohrlich는 무신호 조건을 준수하면서도 치렐슨의 한계를 위반해 양자물리학에서는 실현 불가능한 $상자{\displaystyle }$ P$(a, b$를 확인했다$$.PR 박스라고 불리며 다음과 같이 기술할 수 있습니다.

$({displaystyle P(a,b x,y)=syslogfrac {1}{2}}\syslog_{xy,a\oplus b}).}$

$여기$서 a${\displaystyle ,}$ ${\displaystyle b,}$ ${\displaystyle x,}$(\$displaystyle a, b,$ x, y)는${\displaystyle }$0$,$1(\$displaystyle${0$,1$의 값을 취하며${\displaystyle ,}$ $(\displaystyle$ a$\oplus$ b$)$는 모듈로 2의 합을 나타냅니다.이 상자의 CHSH 값이 4인 것을 확인할 수 있습니다(Tsirlon $바운드{\displaystyle \mathrm{}}$ ${\displaystyle 22}$2.$({displaystyle$ 2${\sqrt {2}}\약$2.$828).$이 상자는 이전에 라스톨^[55], 칼핀, 치렐슨에 ^[56]의해 확인되었습니다.

이러한 불일치의 관점에서, Popescu와 Rohrlich는 양자 상관관계를 도출할 수 있는 무신호 조건보다 더 강한 물리적 원리를 식별하는 문제를 제기한다.몇 가지 제안이 뒤따랐다.

1. Non-trival Communication Complexity(NTCC;^[57] 단순하지 않은 통신 복잡도).이 원칙은 비국소적 상관관계가 두 당사자가 단 의 $통신비트를 사용$하여 p$>$ 1/$2$의 로 모든 단방향 통신문제를 해결할 수 있을 정도로 강해서는 안 된다고 규정하고 $있습니다$.Tirelson's bound by ${\displaystyle 2\sqrt{\mathrm{}}}$ $2{\displaystyle \mathrm{}}$( ${\displaystyle 2\frac{\mathrm{}}{}\frac{\sqrt{3\mathrm{}}}{}}$ -${\displaystyle 1)\approx }$ 0 . ${\displaystyle 4377}$( \ $displaystyle$2 \ $sqrt$ {$2$} \ left ( { \ $frac$ { } { \ $sqrt$ {3} $- 1$ \ right $)\ 약$0 . $4377$ ts ts ts ts it it it it it it it it 0 0 it it it it it it it 2 . 4377 。
2. Non Local Computation(NANLC;^[58] 로컬 이외의 계산)에는 이점이 없습니다.다음 시나리오가 고려됩니다.$f{\displaystyle {}_{}^{}}$ ${\displaystyle {0\mathrm{}}_{}^{}}$, ${\displaystyle 1_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ { \ $displaystyle$ f$_$ {$0$ ,$1$\$to$ 1$\}$ 의 $경우$, 2 개의 파티는 n$${\ $displaystyle$ n$}$ $bits$ x ,$$ { \ $displaystyle$x , $y$$$} 의$$ $스트링$을 분배하고${\displaystyle ,}$ ${\$ $displaystyle$ a, b$}$ 의$$ $비트$ $출력$을 $요구받습니다{\displaystyle }$.$f{\displaystyle }$( ${\displaystyle xy}$y$$) { $displaystyle$f ($x$ \ $oplus$y )$$uess 。NANLC의 원칙에는 로컬이 아닌 박스가 이 게임을 플레이하는 데 있어 양 당사자에게 어떠한 이점도 주어서는 안 된다고 명시되어 있습니다.치렐슨의 경계를 위반하는 어떤 상자라도 그런 이점을 제공할 수 있음이 증명되었다.
3. 정보원인성(IC).^[59]시작점은 초당적 통신 시나리오로, 부품(Alice) 중 하나에 n개$(\displaystyle$ n$)$ 비트의 $랜덤{\displaystyle }$ $문자열{\displaystyle }$x(\$style$ x$)$가 건네집니다.두 번째 부분인 Bob은 k ${\displaystyle \{}$ {${\displaystyle 1}$,${\displaystyle }$. , n $}$ { $display style$k \ $in$\ { $1$, , $n$\ }$$$a{\displaystyle }$ a a 。이들의 목표는 Bob에게$$ k $비트$(\$displaystyle x_$$k{\displaystyle {}_{}}$})를 전송하는 것입니다.이것에 의해 Alice는 $Bob{\displaystyle }$ s$\displaystyle$ s$\$bits를$$ 전송할 수 있습니다.IC의 원리는 앨리스의 비트와 밥의 추측 사이의 상호 정보 $(\displaystyle$ k$)$의 합계는 앨리스가 전송한 비트 $수{\displaystyle }$ s$(\displaystyle$ s$)$를 초과할 수 없음을 나타냅니다.치렐슨의 경계를 위반하는 어떤 상자든 두 당사자가 IC를 위반할 수 있는 것으로 나타났습니다.
4. 거시적 국소성(ML).^[60] 검토된 설정에서는 독립적으로 준비된 다수의 상관 입자 쌍에 대해 두 개의 개별 당사자가 광범위한 저해상도 측정을 수행합니다.ML은 이러한 "거시적" 실험은 로컬 숨겨진 변수 모형을 허용해야 한다고 말합니다.치렐슨의 한계를 위반할 수 있는 어떤 현미경 실험도 거시적 척도로 가져올 때 표준 벨의 비국소성을 위반할 수 있다는 것이 증명되었다.치렐슨의 결합 외에도 ML의 원리는 모든 2점 양자 상관자 집합을 완전히 복구합니다.
5. 로컬 직교성(LO)^[61]이 원칙은$$n개의 \$displaystyle$n이$$ 각각 x${\displaystyle {}_{}{1\mathrm{}}_{}}$,${\displaystyle }$.${\displaystyle }$. , x$$ \ $displaystyle x_{1},$ ...$x_{$n$$}개의 로컬 랩에서 $실험$을 $수행$하는 다단계 벨 시나리오에 적용됩니다.이들은 각각${\displaystyle {}_{}}$1, ${\displaystyle ...,}$ $(\$1}..., $a_{n$의 $결과$를 얻습니다.벡터${\displaystyle 쌍\stackrel{}{}}$( 「 ${\displaystyle x\stackrel{}{}}$ ${\displaystyle 」}$ $){$ $displaystyle {\bar${a$}}{$bar ${x$$}}})$은 이벤트라고 불립니다.2개의 ${\displaystyle 이벤트\stackrel{}{}}$${\displaystyle {(\{\backslash }^{\mathrm{}}}$$displaystyle({\$${\displaystyle bar{}^{}{\stackrel{}{}}^{}}$${a$${\displaystyle {}^{}}$ ${\$$bar {x$$\}\})$$${{$displaystyle}$ {\prime}${{\$bar {a}} ${{\prime}}})$는 x $= xdisplay$ $style$ {$x}$ {\prime$}$ {\$prime$})이$$ 존재하는 $경우{\displaystyle }$ 로컬 직교한다고 합니다.=${\displaystyle {a\_}_{}}${k}^{\prime }가 ${\displaystyle {아닌}_{}^{}}$k$′$ $。$LO의 원리는 모든 다중 부분 상자에 대해 쌍으로 국소적으로 직교하는 사건 집합의 확률 합계가 1을 초과할 수 없음을 나타냅니다.0.$({displaystyle$0.$052)$의 양으로 묶인 초당 박스를 위반하면 LO를 위반하는 것으로 입증되었습니다.

이 모든 원칙들은 실험적으로 조작될 수 있습니다. 두 개 이상의 사건들이 공간처럼 분리되어 있는지 여부를 결정할 수 있다는 가정하에서요.이것은 이 연구 프로그램을 일반화된 확률론적 이론을 통한 양자 역학의 자명한 재구성과는 별도로 한다.

위의 작업은 ^[62]배선 하에서 모든 물리적 상관관계 세트를 닫아야 한다는 암묵적인 가정에 의존합니다.즉, 고려된 세트 내에서 다수의 박스의 입력과 출력을 조합하여 제작된 모든 유효 박스도 세트에 속해야 합니다.배선 하에서의 폐로는 CHSH의 최대치에 제한을 가하지 않는 것으로 보인다.그러나, 이것은 무효 원칙이 아니다. 반대로, 확률 공간에서의 많은 단순하고 직관적인 일련의 상관관계가 우연히 그것을 위반한다는 것을 보여준다.

원래, 이러한 원칙(또는 해당 하위 집합)충분히 모든 제약 조건}Q¯{\displaystyle{\bar{Q}정의를 도출하기 위해}이 강했다. 이런 사태를 몇년 동안은 거의 양자의 건설 Q일{\displaystyle{\tilde{Q}을 세웠다까지 계속되었다}}.[63]Q일{\와 같이 알려지지 않았다.disp$laystyle${\$tilde {Q}}$은(는) 배선 하에서 닫히는 상관 관계 집합으로, 반무한 프로그래밍을 통해 특성화할 수 있습니다.$Q$ c${\displaystyle {}_{}q\stackrel{}{}}$ Q $、$ { $displaystyle Q _$ { c$$} \ $supset$ \ subset }$$${\displaystyle {}_{}}$ also also also also also p p q qP${\displaystyle }$(${\displaystyle a}$ ,${\displaystyle b}$ ,${\displaystyle y}$ ${\displaystyle )\notin Q_{}}$c c \ $displaystyle$P ($a$ ,$x$ ,$y$ )\$not \in$ Q _ { c$\}$ set within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within within $within{\displaystyle }$ within within within within within within또한 거의 퀀텀 박스가 IC를 준수한다는 수치적 증거도 있다.따라서, 위의 원칙들이 함께 취해진다고 해도, 두 개의 입력과 두 ^[63]개의 출력으로 이루어진 가장 단순한 벨 시나리오에서 양자 집합을 제외하기에는 충분하지 않은 것으로 보인다.

디바이스 독립형 프로토콜

논로컬리티는 실험에 관련된 준비 및 측정 장치의 내부 작동에 대한 지식에 의존하지 않는 양자 정보 작업을 수행하기 위해 이용될 수 있다.이러한 프로토콜의 보안 또는 신뢰성은 실험적으로 측정된 상관 $관계{\displaystyle }$ P$a$ ${\displaystyle b}$ x${\displaystyle ,}$ $)$ {\$displaystyle$ P$(a,$b$x,y$의 강도에 따라 달라집니다. 이러한 프로토콜을 장치 독립형 프로토콜이라고 합니다.

디바이스에 의존하지 않는 양자 키 배포

이 원시적인에서는 첫번째 장치 독립성의 프로토콜 제안한 것으로 장치 독립성의 양자 키 분배(QKD)[64], 두 먼 파티, 앨리스와 밥, 그들이 탐사하는데, 따라서 통계 P(a, b), y){P(a,b x,y)\displaystyle}를 얻고자 했다. 어떻게 비국부적 그 상자 P(a에 기초한 뒤엉킨 양자 상태 분포한다b${\displaystyle x}$,${\displaystyle y}$ $)({displaystyle$ P$(a,$b$x, y)}$는 우연히도 앨리스와 밥의 출력 값에 대해 외부 양자 대항마인 이브(도청자)가 얼마나 많은 지식을 가질 수 있는지를 앨리스와 밥이 추정합니다.이러한 추정을 통해 그들은 앨리스와 밥이 완벽하게 상관된 일회성 패드를 공유하는 화해 프로토콜을 고안할 수 있습니다. 이브는 아무런 정보도 가지고 있지 않습니다.그런 다음 원타임 패드를 사용하여 퍼블릭채널을 통해 비밀 메시지를 전송할 수 있습니다.디바이스에 의존하지 않는 QKD에 대한 첫 번째 보안 분석은 Eve가 특정 패밀리의 ^[65]공격을 수행하는 데 의존했지만, 최근 이러한 모든 프로토콜이 무조건 ^[66]안전한 것으로 입증되었습니다.

디바이스에 의존하지 않는 랜덤성 인증, 확장 및 증폭

비국소성은 벨 실험에서 당사자 중 한 명의 결과가 ^[67]외부 상대에게 부분적으로 알려지지 않았음을 증명하기 위해 사용될 수 있다.부분 랜덤 시드를 여러 비로컬박스에 공급하고 출력을 처리한 후 유사한 랜덤성의^[68] 긴(잠재적으로 무제한) 문자열 또는 더 짧지만 더 많은 랜덤 ^[69]문자열을 얻을 수 있습니다.이 마지막 원시는 고전적인 ^[70]환경에서는 불가능하다는 것을 증명할 수 있다.

자가 테스트

Alice와 Bob이 공유하는${\displaystyle }상자{\displaystyle P}$(${\displaystyle a,}$ ${\displaystyle b}$ x${\displaystyle ,}$ y$)$ {$displaystyle P(a, b x,$ y)}는 고유한 양자 실현만 허용됩니다.즉, 측정 $연산자{\displaystyle {}_{}^{}}$ ${\displaystyle E_{}^{}}$ ${\displaystyle {}_{}^{}}$x , ${\displaystyle F_{}^{}}$ b$$ {\$displaystyle E_{a}^{x}$가 존재함을 의미합니다.$F_{b}^{y}$ 및$$ 양자 상태 $({$로 인해$(a,$ $x, y)$가 발생하며 다른 물리적 실현${\displaystyle {\stackrel{}{}}_{}^{}}$E ~ ${\displaystyle {}_{}^{}}$,${\displaystyle {\stackrel{}{}}_{\stackrel{}{}}^{}}$ ~ ${\displaystyle {}_{}^{}}$ ~${\displaystyle {}_{}^{}y\stackrel{}{}}$ ~$$ ~ { $display$ $style$$${ $tilde$}^{a$}^{a$})가$됩니다$.${\displaystyle P}$의${\displaystyle }$\$right$${\displaystyle \backslash \mathrm{rangle}}$ $}$( a , b x ,${\displaystyle }$y$$) {{ $displaystyle P$ ( a ,$b$x , y$$$$) }는${\displaystyle {}_{}^{}}$E ${\displaystyle a_{}^{}}$ x , F b${\displaystyle {}_{}^{}}$ , ${\displaystyle \psi }$ {\$$displaydisplaydisplaydisplay{ $display style$ E _ { $a$}^{ $x$} 에 $접속$되어 있습니다$.$$로컬 유니터리$ 변환을 통해 $F_{$b$$$}^{y},\left$ \$psi$ \right\rangle$}.$디바이스 의존형 양자 단층 촬영의 한 예로 해석될 수 있는 이 현상은 치렐슨에^[37] 의해 처음 지적되었고 메이어스와 ^[64]야오에 의해 자가 테스트라고 명명되었다.자가 테스트는 시스템 노이즈에 대해 견고한 것으로 알려져 있습니다. 즉, 실험적으로 측정된 통계가 P${\displaystyle (a,}$ ${\displaystyle b}$x,${\displaystyle y})\backslash$$style$ P$(a,$ b $x,y)\$display에 $충분히{\displaystyle }$ 가깝다면 기본 상태 및 측정 연산자를 오류 ^[64]막대까지 결정할 수 있습니다.

치수 증인

양자 $상자{\displaystyle }$ P${\displaystyle (a}$, ${\displaystyle b}$x ,${\displaystyle y}$)의 위치 외 정도({$displaystyle$ P$(a,$b x$,y)}$도 Alice 및 ^[71]Bob이 액세스할 수 있는 로컬 시스템의 Hilbert 공간 치수에 하한을 제공할 수 있습니다.이 문제는 완전 양의 ^[72]반무한 순위가 낮은 행렬의 존재를 결정하는 것과 같다.통계를 기반으로 힐베르트 공간 차원에 대한 하한을 찾는 것은 어려운 일이며, 현재의 일반 방법은 매우 낮은 ^[73]추정치만 제공한다.그러나, 5개의 입력과 3개의 출력이 있는 벨 시나리오는 기본 힐베르트 공간 ^[74]차원에 임의로 높은 하한을 제공하기에 충분하다.앨리스와 밥의 시스템의 국소적 차원에 대한 지식을 가정하지만, 그 외에는 관련된 준비 및 측정 장치의 수학적 기술에 대한 주장을 하지 않는 양자 통신 프로토콜을 반디바이스 독립 프로토콜이라고 한다.현재 양자 키 배포 및 임의성 ^[76]확장을 위한 반디바이스 독립 프로토콜이 존재한다.

「 」를 참조해 주세요.

• 원거리 액션
• 포퍼의 실험
• 양자 유사 텔레파시
• 양자문맥성
• 양자 기초

레퍼런스

추가 정보

• Grib, AA; Rodrigues, WA (1999). Nonlocality in Quantum Physics. Springer Verlag. ISBN 978-0-306-46182-8.
• Cramer, JG (2015). The Quantum Handshake: Entanglement, Nonlocality and Transactions. Springer Verlag. ISBN 978-3-319-24642-0.
• Duarte, FJ (2019). Fundamentals of Quantum Entanglement. Institute of Physics (UK). ISBN 978-0-7503-2226-3.