마하수

이 문서의 선두 부분을 다시 써야 할 수 있습니다. 리드 레이아웃 가이드를 사용하여 섹션이 Wikipedia의 규범을 따르고 모든 필수 세부사항을 포함하도록 하십시오. (2021년 3월) (이 템플릿메시지를 삭제하는 방법과 시기에 대해 알아보기)

마하수(M 또는 Ma)(/mµµk/; 독일어: [max])는 유체역학에서 국소 ^[1][2]음속에 대한 유속 비율을 나타내는 무차원량이다.

${\displaystyle \mathrm {M} = flac {u}{c}}$

여기서:

M은 로컬 마하 수치입니다.

u는 경계에 관한 국소 유속(흐름에 담근 물체 등 내부 또는 채널 등 외부)입니다.

c는 매체의 음속이며, 공기 중의 음속은 열역학 온도의 제곱근에 따라 달라집니다.

정의에 따르면 마하 1에서 국소 유속 u는 음속과 같다.마하 0.65에서 u는 음속의 65%(아음속)이며, 마하 1.35에서 u는 음속(슈퍼소닉)보다 35% 더 빠릅니다.고고도 항공 우주 비행기의 조종사들은 비행 마하 수치를 사용하여 실제 비행 속도를 표현하지만, 차량 주변의 흐름장은 3차원으로 변화하며, 이에 상응하는 국부 마하 수치와 함께 변화한다.

음속과 마하 수치는 주변 가스의 온도에 따라 달라집니다.마하 수치는 주로 흐름을 압축할 수 없는 흐름으로 취급할 수 있는 근사치를 결정하기 위해 사용됩니다.매체는 기체 또는 액체일 수 있습니다.경계가 매체 내에서 이동할 수도 있고 매체가 매체를 따라 흐르는 동안 정지해 있을 수도 있고 둘 다 다른 속도로 움직일 수도 있습니다. 중요한 것은 서로에 대한 상대 속도입니다.경계는 매체에 담근 물체의 경계 또는 매체를 통과하는 노즐, 확산기 또는 풍동 등의 채널의 경계일 수 있습니다.마하수는 2단계의 비율로 정의되기 때문에 무차원 수치입니다.M < 0.2~0.3이고 흐름이 준안정적이고 등온일 경우 압축성 효과는 작으며 단순화된 비압축성 흐름 방정식을 ^[1][2]사용할 수 있다.

어원학

마하 수치는 모라비아의 물리학자이자 철학자인 에른스트 ^[3]마하의 이름을 따서 명명되었으며,^[4] 1929년 항공 기술자 야콥 아크레트가 제안한 명칭이다.마하 수는 측정 단위가 아닌 무차원 양이기 때문에 단위 뒤에 오며, 두 번째 마하 수는 2 마하(또는 마하)가 아닌 마하 2입니다.이것은 최초의 단위였던 초기의 현대 해양 측심 단위 마크(pathom의 동의어)를 다소 연상시키며 마하라는 용어의 사용에 영향을 미쳤을 수 있다.인간이 소리보다 빠르게 비행하기 이전 10년 동안, 항공 기술자들은 음속을 마하 ^[5]1이 아닌 마하 1의 수치로 언급했습니다.

개요

마하 수치는 유체 흐름의 압축성 특성을 나타내는 척도입니다. 유체(공기)는 다른 ^[6]변수에 관계없이 주어진 마하 수치에서 압축성의 영향을 받아 유사한 방식으로 작동합니다.국제 표준 대기에서 모델링한 바와 같이, 평균 해수면에서의 건조한 공기, 15°C(59°F)의 표준 온도, 음속은 초당 340.3m(1,116.5ft/s; 761.23mph; 661.49kn)^[7]이다.소리의 속도는 일정하지 않다; 기체에서는 절대 온도의 제곱근에 비례하여 증가하며, 일반적으로 해수면과 11,000 미터(36,089 피트) 사이의 고도가 증가함에 따라 대기 온도가 감소하기 때문에, 소리의 속도 또한 감소한다.예를 들어, 표준 대기 모델은 11,000m(36,089ft) 고도에서 -56.5°C(-69.7°F)까지 온도를 낮추며, 이에 상응하는 음속(Mach 1)은 초당 295.0m(967.8ft/s; 659.9mph; 573.4), 86.7%의 해수면 값에 해당합니다.

마하 체계의 분류

가장 순수한 의미에서 아음속과 초음속이라는 용어는 각각 로컬 음속보다 낮은 속도와 그 이상의 속도를 의미하지만, 공기역학자들은 종종 마하 값의 특정 범위에 대해 같은 용어를 사용합니다.이는 아음속 설계에 사용된 Navier-Stokes 방정식의 근사치가 더 이상 적용되지 않는 비행(자유 스트림) M = 1 주위의 천음속 상태 때문에 발생한다. 가장 간단한 설명은 자유 스트림 마하 수치가 이 값보다 낮더라도 기체 주변의 흐름이 국소적으로 M = 1을 초과하기 시작한다는 것이다.

한편, 초음속 정위는 보통 선형화 이론을 사용할 수 있는 마하 수, 예를 들어 (공기) 흐름이 화학적으로 반응하지 않는 경우, 그리고 공기와 차량 사이의 열 전달이 계산에서 상당히 무시될 수 있는 경우에 대해 이야기하는데 사용됩니다.

다음 표에서는 아음속과 초음속이라는 단어의 순수한 의미가 아니라 마하 값의 범위 또는 범위를 참조합니다.

일반적으로 NASA는 높은 극초음속도를 10에서 25 사이의 마하 수치로 정의하고 재진입 속도를 마하 25보다 큰 수치로 정의합니다.이 체제에서 운용되는 항공기는 우주왕복선과 개발 중인 다양한 우주 비행기들을 포함한다.

정권	비행 속도					일반적인 평면 특성
	(마하)	(표준)	(mph)	(km/h)	(m/s)
아음속	0.8 미만	530 미만	609 미만	980 미만	273 미만	대부분의 경우 프로펠러식 상용 터보팬 항공기로 높은 종횡비(슬렌더) 날개와 노즈 및 앞쪽 가장자리와 같은 둥근 특징을 가지고 있습니다. 아음속 범위는 항공기의 모든 기류가 마하 1보다 작은 속도 범위입니다.임계 마하 수(Mcrit)는 항공기의 모든 부분의 기류가 먼저 마하 1에 도달하는 최저 자유 흐름 마하 수이다.따라서 아음속 범위에는 Mcrit보다 낮은 모든 속도가 포함됩니다.
트랜스오닉	0.8–1.2	530–794	609–914	980–1,235	273–409	트랜스오닉 항공기는 거의 항상 날개를 쓸어내 항력-분산 지연을 유발하며 종종 휘트콤 영역 규칙의 원칙을 준수하는 설계를 특징으로 한다. 천음속 범위는 항공기의 다른 부분의 기류가 아음속과 초음속 사이의 속도 범위입니다.그래서 Mcrit에서 마하 1.3까지의 비행 체계를 트랜조닉 레인지라고 부릅니다.
초음속	1.2–5.0	794-3,308	915-3,806	1,235–6,126	410–1,702	초음속 범위는 항공기 상의 모든 기류가 초음속(마하 1 이상)인 속도 범위입니다.그러나 선행 가장자리를 충족하는 기류는 처음에는 감속되므로 항공기 상에서의 모든 흐름이 초음속임을 보장하기 위해 자유 흐름 속도가 마하 1보다 약간 더 커야 합니다.일반적으로 초음속 범위는 마하 1.3보다 큰 자유류 속도로 시작한다. 초음속으로 비행하도록 설계된 항공기는 마하 1을 초과하는 흐름의 급격한 차이 때문에 공기역학적 설계에서 큰 차이를 보인다.날카로운 모서리, 얇은 에어로포일 섹션, 움직이는 테일플레인/캐너 등이 일반적입니다.현대 전투기는 저속 조종을 유지하기 위해 타협해야 한다; "진정한" 초음속 디자인은 F-104 스타파이터, MiG-31, 북미 XB-70 발키리, SR-71 블랙버드, BAC/에로 스페이스 콩코드 등을 포함한다.
극초음속	5.0–10.0	3,308–6,615	3,806–7,680	6,126–12,251	1,702–3,403	마하 6.72의 X-15는 가장 빠른 유인 항공기 중 하나이다.또한 냉각된 니켈-티타늄 피부, 고도로 통합된(간섭 효과의 지배로 인해 비선형 거동은 별도의 구성요소에 대한 결과의 중첩이 무효임을 의미), 마하 5 X-51A 웨이버라이더와 같은 작은 날개.
극초음속	10.0–25.0	6,615–16,537	7,680–19,031	12,251–30,626	3,403–8,508	마하 9.6의 NASA X-43은 가장 빠른 항공기 중 하나이다.열 제어는 설계상의 주요 고려사항이 됩니다.구조물은 고온으로 작동하도록 설계되거나 특수 규산염 타일 등으로 보호되어야 합니다.화학적으로 반응하는 흐름은 차량의 피부 부식을 유발할 수도 있으며, 자유 원자 산소가 매우 빠른 흐름을 특징으로 합니다.극초음속 설계는 곡률 반경이 감소하면서 상승하는 공기역학적 가열 때문에 종종 무딘 구성으로 강제됩니다.
재진입 속도	25.0 이상	16,537 이상	19,031 이상	30,626 이상	8,508 이상	열차폐, 날개 작거나 없음, 뭉툭한 모양.러시아의 아방가르드(초음속 활공차)는 마하 27에 이른다.

물체 주위의 고속 흐름

비행은 대략 6가지 범주로 분류할 수 있다.

정권	아음속	트랜스오닉	음속	초음속	극초음속	고속화
마하	0.8 미만	0.8–1.2	1.0	1.2–5.0	5.0–10.0	8.8 이상

비교를 위해: 낮은 지구 궤도에 필요한 속도는 높은 고도에서 공기 중 약 7.5km/s = 마하 25.4이다.

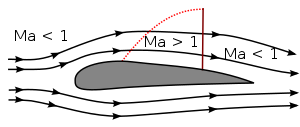
천음속에서는 물체 주위의 흐름장은 아음속 및 초음속 부분을 모두 포함한다.트랜소닉 기간은 M >1 흐름의 첫 번째 존이 오브젝트 주위에 표시되었을 때 시작됩니다.(항공기의 날개와 같은) 에어포일의 경우, 이는 일반적으로 날개 위에서 발생합니다.초음속 흐름은 정상적인 충격에서만 아음속으로 감속할 수 있다. 이는 일반적으로 후연 전에 발생한다. (그림 1a)

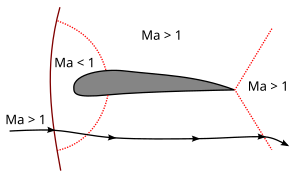
속도가 증가함에 따라 M >1 플로우존은 선행 및 후행 양쪽 에지를 향해 증가합니다.M = 1에 도달하고 통과할 때, 정상적인 충격은 후행 가장자리에 도달하고 약한 사선 충격이 됩니다. 즉, 유량은 충격에 따라 감속하지만 초음속 상태를 유지합니다.물체의 전방에서 정상적인 충격이 발생하며 흐름장의 유일한 아음속 영역은 물체의 앞쪽 가장자리 주변의 작은 영역이다. (그림 1b)

(a)	(b)

그림 1 에어포일 주위의 트랜조닉 에어플로우에서의 마하수(M < 1 (a) 및 M > 1 (b)).

항공기가 마하 1(즉, 방음벽)을 초과할 경우 항공기 바로 앞에 큰 압력 차이가 발생한다.충격파라고 불리는 이 갑작스러운 압력 차이는 원뿔 모양(이른바 마하 콘이라고 함)으로 항공기에서 뒤로 그리고 바깥쪽으로 퍼집니다.이 충격파가 빠르게 움직이는 항공기가 머리 위로 이동할 때 들리는 소닉 붐을 일으킨다.항공기 안에 있는 사람은 이 소리를 듣지 못할 것이다.속도가 높을수록 원뿔은 더 좁아진다. M = 1 바로 위에서는 원뿔이 거의 아니지만 약간 오목한 평면에 가깝다.

완전 초음속에서는 충격파가 원뿔 모양을 띠기 시작하고 흐름은 완전히 초음속이거나, 또는 (무딘 물체의 경우) 물체의 코와 전방에서 발생하는 충격파 사이에 아주 작은 아음속 흐름 영역만 남습니다.(날카로운 물체의 경우, 코와 충격파 사이에 공기가 들어가지 않습니다.충격파는 코에서 시작됩니다.

마하 수치가 증가함에 따라 충격파와 마하 콘의 강도도 점점 좁아집니다.유체의 흐름이 충격파를 통과할 때 유체의 속도가 감소하고 온도, 압력 및 밀도가 높아집니다.충격이 강할수록 변화는 커집니다.마하 수치가 충분히 높으면 충격에 의해 온도가 너무 높아져 충격파의 배후에 있는 가스 분자의 이온화와 해리가 시작됩니다.이러한 흐름을 극초음속이라고 합니다.

극초음속 속도로 이동하는 물체도 마찬가지로 코 충격파 뒤에 있는 기체와 같은 극단적인 온도에 노출되므로 내열성 물질의 선택이 중요합니다.

채널 내의 고속 흐름

채널의 흐름이 초음속이 되면 한 가지 중요한 변화가 일어납니다.질량 유량 보존은 유량 채널을 수축시키면 유속이 증가할 것으로 예상하게 되며(즉, 채널을 좁혀서 공기 흐름을 더 빠르게 만든다) 아음속에서는 이것이 그대로 유지된다.그러나 일단 흐름이 초음속이 되면 흐름 면적과 속도의 관계가 역전됩니다. 즉, 채널을 확장하면 실제로 속도가 증가합니다.

그 결과 초음속으로의 흐름을 가속화하려면 수렴 노즐이 필요한데, 수렴 노즐은 수렴 구간이 음속으로의 흐름을 가속하고 발산 구간이 가속을 계속한다.이러한 노즐은 드 라발 노즐이라고 불리며 극단적인 경우 극초음속 속도에 도달할 수 있습니다(20°C에서 마하 13 (15,900 km/h; 9,900 mph).

항공기 마하미터 또는 전자비행정보시스템(EFIS)은 정체압(피토튜브) 및 정압에서 도출된 마하수를 표시할 수 있다.

계산

음속이 알려지면 항공기가 비행하는 마하 수치는 다음과 같이 계산될 수 있다.

${\displaystyle \mathrm {M} = flac {u} {c}}$

여기서:

M은 마하 수

u는 움직이는 항공기의 속도이고

c는 특정 고도에서의 음속입니다(더 적절한 온도).

는 열역학적 온도에 그리고 소리의 속도 다양하게:.

$(T}},}.$

여기서:

기체의 비열의 일정한 압력은 일정 부피(1.4공기를 위해)에 난방을 할에서γ{\displaystyle \gamma\와 같이,}비율입니다.

R({\displaystyle R_{*}}구체적인 가스 공기에 상수입니다.

T,{\displaystyle T,}은 정적 대기 온도이다.

만약 소리의 속도는 알려지지 않았다, 마하수(정적 및 동적)고 1.0이하 마하 번호를 베르누이 방정식에서 파생된 다음 공식을 이용하여 다양한 공기 압력을 측정하여 결정할 수 있다.공기는 이상 기체, 공식은 아음속의 압축성 유동에서는 마하 수를 계산하기 위해 가정:[8] 있다.

${\displaystyle \mathrm{M}={\sqrt{{{2\frac}{\gamma)}}\left[\left({\frac{q_{c}}{p}}+1\right)^{\frac{\gamma)}{\gamma}}-1\right]}}\,}.$

여기서:

Qc은 충격 압력(동압력).

p은 정압

기체의 비열의 일정한 압력은 일정 부피(1.4공기를 위해)에 난방을 할에서γ{\displaystyle \gamma\와 같이,}비율입니다.

R({\displaystyle R_{*}}구체적인 가스 공기에 상수입니다.

초음속 압축 흐름에서 마하 수를 계산하는 공식은 레일리 초음속 피토 방정식에서 도출됩니다.

${\displaystyle {p_{t}}= left[{\frac +1} {M} ^{2}\right]^{\frac {\frac }{\frac -1}\cdot \left[{\frac +1-\fac +2\fac +\mathram {M2}} ^{\right} }$

피토 튜브 압력에서 마하 수치 계산

마하 수치는 온도와 실제 대기 속도의 함수입니다.그러나 항공기 비행 계기는 온도가 아닌 마하 수치를 계산하기 위해 압력 차이를 사용하여 작동한다.

공기가 이상적인 기체라고 가정할 때, 아음속 압축 흐름의 마하 수를 계산하는 공식은 M < 1에 대한 베르누이의 방정식에서 구할 수 있다.^[8]

${{displaystyle \mathrm {M} = left[\left\frac {q_{c}} {p}} + 1\right]^{\frac {2}-1\right]}},$

초음속 압축 흐름에서 마하 수를 계산하는 공식은 공기에 대한 매개변수를 사용하여 레일리 초음속 피토 방정식(위)에서 찾을 수 있습니다.

$\displaystyle \mathrm {M} \약 0.88128485{\sqrt {left({\frac {q_{c}}{p}}}+1\right)\left(1-{\frac {1}{7},\mathrm {M}}}\right)^{2}^2.5}}}}$

여기서:

q는_c 정상적인 충격 뒤에 측정된 동적 압력입니다.

볼 수 있듯이, M은 방정식의 양쪽 측면에와 실용적인 목적으로root-finding 알고리즘은 수치 햇법 M2유통에7th-order 다항식의 자세한 내용은 방정식의 해결 방안은 뿌리를 자르고, 비록 몇몇 이들의 명시적으로 해결될 수 있는 경우, Abel–Ruffini 정리한 그 뿌리를 어떠한 일반적인 형태 존재하는 사용해야 하는 것으로 보인다. of 이 다항식).먼저 아음속 방정식에서 M을 계산하여 M이 1.0보다 큰지 여부를 판정한다.이 시점에서 M이 1.0보다 크면 아음속 방정식의 M 값이 초음속 방정식의 고정점 반복의 초기 조건으로 사용되며, 보통 매우 빠르게 수렴한다.^[8]또는 뉴턴의 방법도 사용할 수 있다.

「 」를 참조해 주세요.

• 임계 마하 수
• 마하미터 – 비행 계기
• 램젯 – 초음속으로 작동하도록 설계된 대기식 제트 엔진
• 스크램젯 – 초음속 기류에서 연소가 발생하는 제트 엔진
• 음속 – 탄성 매체를 통한 음파 속도
• 진기속
• 매그니튜드 순서

메모들

외부 링크

• Gas Dynamics Toolbox 완벽하고 불완전한 가스의 혼합물에 대한 마하 수치와 정상 충격파 매개변수를 계산합니다.
• NASA의 마하 수치 인터랙티브 계산기 페이지.
• NewByte 표준 대기 계산기 및 속도 변환기