트랜스오닉

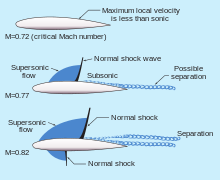
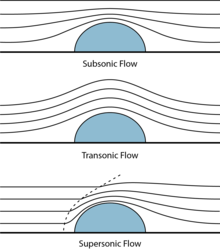
Transonic
미국 회사의 경우 트랜조닉 연소(Transonic 연소)를 참조하십시오.
트랜스오닉 F/A-18 주변 초음속 팽창팬의 공기역학적 응축증거
Sears-Hack 본체는 파형 항력을 최소화하는 단면적 변동을 나타낸다.
충격파는 초임계 날개를 가진 여객기 상공에서 약한 광학 장애로 나타날 수 있습니다.
임계 마하 수치 이상의 흐름 패턴을 나타내는 에어포일의 천음속 흐름 패턴

트랜소닉(또는 트랜스소닉) 흐름은 [1]물체 주위에 아음속 및 초음속 기류 영역을 생성하는 속도로 물체 주위를 흐르는 공기입니다.정확한 속도 범위는 물체의 임계 마하 수에 따라 달라지지만, 천음속 흐름은 음속(해발 343m/s)에 가까운 비행 속도(일반적으로 마하 0.8과 1.2 [1]사이)에서 나타난다.

천음속(또는 천음속) 문제는 2차 세계대전 [2]중에 처음 나타났다.조종사들은 방음벽에 접근하면서 기류가 항공기를 [2]불안정하게 만드는 것을 발견했다.전문가들은 충격파가 하류에서 대규모 분리를 일으켜 항력을 증가시키고 [3]차량 주변의 흐름에 비대칭성과 불안정성을 가중시킬 수 있다는 것을 발견했다.항충격체와 초임계 에어포일을 [3]이용하여 천음속 비행 시 충격파를 약화시키는 연구가 이루어졌다.

대부분의 현대 제트 동력 항공기는 천음속 공기 [4]속도로 작동하도록 설계되어 있다.트랜스오닉 에어스피드는 약 마하 0.8에서 드래그가 빠르게 증가하고 있으며 일반적으로 드래그의 연료비가 대기 속도를 제한한다.파도의 항력을 줄이기 위한 시도는 모든 고속 항공기에서 볼 수 있다.가장 주목할 만한 것은 쓸린 날개를 사용하는 것이지만, 또 다른 일반적인 형태는 휘트콤 지역 규칙의 부작용으로 말벌-허리 동체이다.

천음속도는 헬리콥터와 항공기의 회전자 날개 끝에서도 발생할 수 있다.이로 인해 로터 블레이드에 심한 불균등한 응력이 가해지며 발생할 경우 사고로 이어질 수 있습니다.이는 로터의 크기와 헬리콥터의 전진 속도의 제한 요인 중 하나이다(이 속도가 로터의 전방 스위핑 [선행] 측면에 추가되어 국부적인 트랜스오닉을 일으킬 수 있음).

역사

트랜소닉 에어플로우 검출

속도와 [5]관련된 항공기 비행 문제는 1941년 초음속 시대에 처음 나타났다.시험 비행사인 랄프 버든은 치명적인 [6]비행기 사고로 추락했다.그는 초음속 기류에 의한 충격파가 날개 위로 퍼져 비행기가 [6]정지하는 바람에 조종을 하지 못했다.버든은 마하 0.675의 속도로 음속보다 훨씬 낮게 비행했는데,[5] 이것은 비행기 주위에 다른 기류가 형성된다는 생각을 불러일으켰다.40년대에 켈리 존슨은 압축성이 [5]항공기에 미치는 영향을 조사한 최초의 엔지니어가 되었다.그러나 현대의 풍동에는 천음속 [6]효과를 시험하기 위해 마하 1에 가까운 풍속을 생성할 수 있는 기능이 없었다.얼마 지나지 않아, "트랜소닉"이라는 용어는 "음속 전반"을 의미하는 것으로 정의되었고 NACA의 Hugh Dryden 과 [5]California Institute의 Theodore von Karrmann에 의해 발명되었다.

항공기의 변화

처음에 NACA는 트랜스오닉 [5]비행에 도달할 때 비행기를 안정시키기 위해 "잠수 플랩"을 설계했다.비행기 하부에 있는 이 작은 플랩은 충격파를 막기 위해 비행기를 느리게 만들었지만, 이 디자인은 초음속으로 [5]비행하는 항공기에 대한 해결책을 찾는 것을 지연시킬 뿐이었다.새로운 풍동들이 설계되었기 때문에, 연구원들은 시험 조종사들의 [7]목숨을 위태롭게 하지 않고 새로운 날개 디자인을 시험할 수 있었다.나사(NASA)가 설계한 이 슬롯형 벽면 천음속 터널은 음속에 [7]가장 적합한 날개 끝 모양을 찾기 위해 연구자들이 천음속 공기 중 날개와 다른 날개 모양을 시험할 수 있게 해 주었다.

제2차 세계대전 이후 항공기 설계의 큰 변화가 천음속 [6]비행을 개선하는 것으로 나타났다.항공기를 안정시키는 주된 방법은 비행기 날개의 화음을 바꿔 날개 주변의 기류 속도를 줄이는 것이었는데,[5] 천음파를 막는 한 가지 해결책은 날개 쓸기였다.기류가 날개에 비스듬히 닿기 때문에 날개 두께와 현의 [5]비율이 낮아집니다.날개 모양은 충격파를 방지하고 [8]날개 위의 공기 흐름을 줄이기 위해 상단부가 평평하게 설계되었습니다.나중에, 리차드 휘트콤은 비슷한 [7]원리를 사용하여 최초의 초임계 비행포를 설계했습니다.

수학적 해석

평범하지 않은 뭉툭한 본체([9]파란색) 주위에 3개의 에어플로우 방식(검은색 선)을 합리화합니다.

강력한 컴퓨터가 등장하기 전에는 압축 가능한 흐름 방정식의 가장 단순한 형태도 비선형성 [6]때문에 풀기 어려웠다.이러한 비선형성을 회피하기 위해 사용되는 일반적인 가정은 흐름 내의 교란이 상대적으로 작다는 것입니다.이것에 의해 수학자와 엔지니어는 압축 가능한 흐름 방정식을 비교적 쉽게 풀 수 있는 아음속 또는 초음속 [6]흐름의 미분 방정식 세트로 선형화할 수 있습니다.물체에 의한 교란이 아음속 또는 초음속 흐름보다 훨씬 크기 때문에 이 가정은 근본적으로 사실이 아닙니다.마하 1에 가깝거나 마하 1에 가까운 유속에서는 스트림 튜브(3D 유로)가 물체 주위에 충분히 수축하여 교란이 확산됩니다.[9]공기역학자들이 천음속 흐름에 대한 초기 연구 중에 고전한 이유는 당시 이론이 국소 마하 수치가 1에 가까워짐에 따라 이러한 교란(따라서 항력)이 무한대에 도달했다는 것을 암시했기 때문이다. 이는 알려진 [6]방법을 사용하여 교정할 수 없는 명백한 비현실적인 결과이다.

트랜조닉 플로우 모델의 비선형성을 회피하기 위해 사용된 첫 번째 방법 중 하나는 호도그래프 [2]변환이었습니다.이 개념은 1923년 이탈리아 수학자 프란체스코 트리코미에 의해 처음 탐험되었는데, 그는 압축 가능한 흐름 방정식을 단순화하고 그것들이 [2]해결 가능하다는 것을 증명하기 위해 변환을 사용했다.호도그래프 변환 자체는 Ludwig Frandtl과 O.G.에 의해서도 탐구되었다.1929년 티에젠의 교과서들과 1937년 아돌프 부세만의 교과서들은 이 방법을 천음속 [2]흐름에 특별히 적용하지는 않았다.

독일 수학자이자 브라운슈바이크의 엔지니어인 고트프리드 구들리는 [2]제2차 세계대전이 끝날 무렵 호도그래프 방식을 천음속 흐름에 적용하는 과정에서 트리코미의 작품을 발견했다.그는 트리코미가 도출한 것과 같은 비선형 박공포 압축성 흐름 방정식에 초점을 맞췄지만, 이러한 방정식을 사용하여 에어포일을 통한 흐름을 해결하려는 그의 목표는 독특한 [2][6]과제를 제시했습니다.구데를리와 요시하라 히데오는 부세만으로부터의 입력과 함께 후에 트리코미 방정식의 단수해를 사용하여 이중 쐐기 날개 위의 트랜조닉 흐름의 거동을 해석적으로 풀었는데, 이는 얇은 날개 [2][6]이론의 가정만으로 풀 수 있는 최초의 것이었다.

성공적이긴 했지만, Guderley의 연구는 여전히 이론적인 것에 초점을 맞췄고, 마하 [2]1에서 이중 웨지 에어포일을 위한 단일 솔루션만 만들었습니다.Ames Laboratory의 미국인 엔지니어인 Walter Vincenti는 마하 1과 완전히 초음속 [2]흐름 사이의 천음속 범위를 커버하는 수치 해법으로 Guderley의 마하 1 작업을 보완하는 것을 목표로 했다.빈센티와 그의 조수들은 마하 [2]1 이상의 트랜스오닉 흐름에서 이중 쐐기 날개에 대한 드래그에 대한 4가지 수치 해법을 완성하기 위해 하워드 에몬스의 연구 및 트리코미의 원래 방정식을 이용했다.아음속과 마하 1의 흐름 사이의 간격은 나중에 줄리안 콜과 레온 트릴링에 의해 커버되어 [2]1950년대 초까지 에어포일의 천음속 거동이 완료되었다.

응결 구름

천음속에서는 초음속 팽창팬이 항공기 주변의 다양한 지점에서 저압, 저온 영역을 형성합니다.기온이 이슬점 아래로 떨어지면 눈에 보이는 구름이 형성될 것이다.이 구름들은 비행체가 이동하는 동안 계속 남아 있다.이러한 구름이 형성되기 위해 항공기 전체가 초음속에 도달할 필요는 없다.일반적으로, 항공기의 활이 아음속 비행을 하는 동안 항공기의 꼬리 부분은 초음속 비행에 도달한다.충격파로 끝나는 초음속 팽창팬의 거품이 꼬리를 감싼다.항공기가 가속을 계속함에 따라 초음속 팽창팬이 강해지고 무한대에 도달할 때까지 웨이크 충격파의 크기가 커지며, 이때 활 충격파가 형성된다.이것은 마하 1과 프란틀-글라우르트 특이점입니다.

천문학과 천체물리학에서의 천음속 흐름

천체물리학에서 충격의 증거가 있는 곳(서 있거나, 전파하거나, 진동하는 곳)에서는 초음속 흐름만이 충격을 형성하기 때문에 가까운 흐름은 천음속적이어야 합니다.모든 블랙홀 어카운트는 [10]천음파입니다.이러한 흐름의 대부분은 블랙홀에 매우 가까운 충격도 가지고 있습니다.

젊은 별의 물체나 블랙홀 주변의 원반으로부터의 유출이나 분출은 또한 천음속일 수 있습니다. 왜냐하면 그것들은 음소음속으로 시작되고 먼 거리에서는 항상 초음속이기 때문입니다.초신성 폭발은 초음속 흐름과 충격파를 동반한다.태양풍에서 발생하는 활 충격은 별로부터의 천음속 바람의 직접적인 결과입니다.오랫동안 우리 태양계의 태양권 주변에 활 충격이 존재한다고 여겨져 왔지만,[11] 2012년에 발표된 IBEX 자료에 따르면 그렇지 않은 것으로 밝혀졌다.

「 」를 참조해 주세요.

무료 사전인 Wiktionary에서 transonic을 찾아보세요.

레퍼런스

  1. ^ a b Anderson, John D., Jr. (2017). Fundamentals of aerodynamics (Sixth ed.). New York, NY. pp. 756–758. ISBN 978-1-259-12991-9. OCLC 927104254.
  2. ^ a b c d e f g h i j k l Vincenti, Walter G.; Bloor, David (August 2003). "Boundaries, Contingencies and Rigor". Social Studies of Science. 33 (4): 469–507. doi:10.1177/0306312703334001. ISSN 0306-3127. S2CID 13011496.
  3. ^ a b Takahashi, Timothy (15 December 2017). Aircraft performance and sizing. fundamentals of aircraft performance. p. 107. ISBN 978-1-60650-684-4. OCLC 1162468861.
  4. ^ Takahashi, Timothy (2016). Aircraft Performance and Sizing, Volume I. New York City: Momentum Press Engineering. pp. 10–11. ISBN 978-1-60650-683-7.
  5. ^ a b c d e f g h "Mach 1: Assaulting the Barrier". Air & Space Magazine. Retrieved 14 March 2021.
  6. ^ a b c d e f g h i Vincenti, Walter G. (1997). Engineering theory in the making: Aerodynamic calculation "breaks the sound barrier.". OCLC 1027014606.
  7. ^ a b c "From Engineering Science to Big Science: The NACA and NASA Collier Trophy Research Project Winners. Pamela E. Mack". Isis. 91 (2): 417–418. 2000–2006. doi:10.1086/384834. ISSN 0021-1753.
  8. ^ Hicks, Raymond M.; Vanderplaats, Garret N.; Murman, Earll M.; King, Rosa R. (1 February 1976). "Airfoil Section Drag Reduction at Transonic Speeds by Numerical Optimization". SAE Technical Paper Series. Warrendale, PA: SAE International. 1. doi:10.4271/760477. hdl:2060/19760009938.
  9. ^ a b Ramm, Heinrich J. (1990). Fluid dynamics for the study of transonic flow. New York: Oxford University Press. ISBN 1-60129-748-3. OCLC 228117297.
  10. ^ Chakrabarti, Sandip (1990). Theory of Transonic Astrophysical Flows. Singapore: World Scientific. ISBN 981-02-0204-0.
  11. ^ 를 클릭합니다"NASA – IBEX Reveals a Missing Boundary At the Edge of the Solar System", Science daily, 10 May 2012.