고정점 반복

수치 해석에서 고정점 반복은 함수의 고정점 계산 방법이다.

좀 더 구체적으로, 실제 $f$ 값을 가진 실수에 $f$ 된 함수f {\ $displaystyle f}$ 과 $(와$ ) f {\displaystyle $f}$ 의 도메인에서 $x_{0}$ $x_{0}$ $x_{0}$ 0 $x_{0}$ {\ $displaystyle x_{0}$ 이 주어진 $f$ 경우 고정점 반복은

x_{n+1}=f(x_{n}),\,n=0,1,2,\properties

x $x_{0},x_{1},x_{2},\dots$ $x_{0},x_{1},x_{2},\dots$ $x_{0},x_{1},x_{2},\dots$ , $x_{0},x_{1},x_{2},\dots$ x $x_{0},x_{1},x_{2},\dots$ …의 $x_{0},x_{1},x_{2},\dots$ 시퀀스 x 0, $x_{0},x_{1$ },x_{1 $},x_{2},\dots$ }을 $x_{0},x_{1},x_{2},\dots$ (를) 발생시키며 $x$ $f$ $f$ 이(가) 연속적인 $f$ , 획득한 $x$ ${\displaystystyle x$ i의 고정점임을 $x$ 증명할 수 있다.

f(x)=x.\,

보다 일반적으로 $f$ $f$ 함수는 동일한 공간에 값을 가진 모든 메트릭 공간에서 정의될 $f$ 수 있다.

예

a&gt의 제곱 근을 계산하는){\displaystyle f())={\frac{1}{2}}\left({\frac{}{x}}+x\right)f())12(는 x+))을 취하는 것이}로 첫번째고 유용한 간단한 예는 바빌로니아 법;0,, 즉 x와 a/x의 평균 값의 한계 x는{\displaystyle x={\sqrt{}}}wha(에서에 다가가는 것이다.tever 시작점 $x_{0}\gg 0$ 0 $x_{0}\gg 0$ 0 $x_{0}\gg 0$ $x_{0}\gg 0$ ) 이것은 아래에 인용된 뉴턴의 방법의 특수한 경우다.

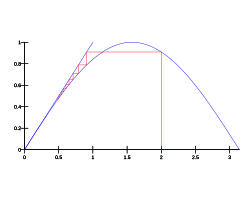
고정점 반복 x_n+1 = sin x와_n 초기값₀ x = 2는 0으로 수렴한다. 이 예는 바나흐 고정점 정리의 가정을 만족시키지 못하므로 수렴 속도는 매우 느리다.

고정점 반복 $x_{n+1}=\cos x_{n}\,$ $x_{n+1}=\cos x_{n}\,$ + 1 $x_{n+1}=\cos x_{n}\,$ = $x_{n+1}=\cos x_{n}\,$ $x_{n+1}=\cos x_{n}\,$ $x_{n+1}=\cos x_{n}\,$ $displaystyle x_{n+1}=\cos x_{n}\,}$ 는 함수 $f(x)=\cos x\,$ $f(x)=\cos x\,$ ) $f(x)=\cos x\,$ = $f(x)=\cos x\,$ cos $f(x)=\cos x\,$ x ${\$ x $\,},$ 모든 시작점 $x_{0}.$ $x_{0}.$ ${\displaystystyle x_{0}$ 의 고유한 $f(x)=\cos x\,$ 고정점으로 수렴한다 $x_{n+1}=\cos x_{n}\,$ . $}$ 이 예는 $x_{0}.$ 바나흐 고정점 정리의 가정을 만족시킨다. Hence, the error after n steps satisfies $x_{n}-x \leq {q^{n} \over 1-q} x_{1}-x_{0} =Cq^{n}$ (where we can take $q=0.85$ , if we start from $x_{0}=1$ .) 일부 상수 q에 대한 $q^{n}$ $q^{n}$ ${\$ 의 배수보다 오차가 적을 때 우리는 선형 수렴을 한다고 말한다. 바나흐 고정점 정리는 선형 수렴으로 고정점 반복을 얻을 수 있도록 한다.
$x_{n+1}=2x_{n}\,$ 지점 반복 $x_{n+1}=2x_{n}\,$ $x_{n+1}=2x_{n}\,$ + 1 $x_{n+1}=2x_{n}\,$ = 2 $x_{n+1}=2x_{n}\,$ $x_{n+1}=2x_{n}\,$ $displaystyle x_{n+1}=2x_{n}\,}$ 은(는) x $x_{0}=0$ = $x_{0}=0$ $x_{0}=0$ 이(가) 아닌 한 분산된다 $x_{n+1}=2x_{n}\,$ $x_{0}=0$ $f(x)=2x\,$ 는 f $f(x)=2x\,$ ( $f(x)=2x\,$ ) $f(x)=2x\,$ = $f(x)=2x\,$ $f(x)=2x\,$ ${\$ 의 고정 지점이 퇴보하고 있다고 $f(x)=2x\,$ 말한다.
다음 예에서 알 수 있듯이 f가 연속적이라는 요건은 중요하다. 반복 $x_{n+1}={\frac {x_{n}:{2}},&x_{n}\neq 0\1,&x_{n}=0\end{case}}}}}}}$ x $x_{0}$ ${\$ 의 모든 값에 대해 0으로 수렴한다 $x_{0}$ 단, 0은 함수의 고정점이 아니다. $f(x)={\fract{x}{x}{2}},&x\neq 0\1,&x=0\end{case}}}$ $x=0$ 함수는 x $x=0$ = $x=0$ ${\displaystyle x=0$ 에서 연속되지 않으며, 실제로 고정된 점이 없기 때문이다.

적용들

뉴턴이 주어진 서로 다른 함수 $f(x)$ ) $f(x)$ 의 루트를 찾는 방법은 $f(x)$ x ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ + ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ = ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ - ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ ( ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ n ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ ) f ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ ( ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ ) ${\textstyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.}$ . ${\textstyle x_{n+1}=x_{n}-{f(x_{n}){f(x_{n}}}}}}}}}}.$ $}$
${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ( ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ = x ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ - ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ( ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ${\textstyle g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\$ 을 $($ 를) 쓰면 뉴턴 반복을 ${\textstyle x_{n+1}=g(x_{n})}$ ${\textstyle x_{n+1}=g(x_{n})}$ x ${\textstyle x_{n+1}=g(x_{n})}$ + ${\textstyle x_{n+1}=g(x_{n})}$ = g $(x_{n})$ 로 다시 쓸 수도 있다 ${\textstyle x_{n+1}=g(x_{n})}$
이 반복이 ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ 의 고정점 $x$ 로 수렴되면 ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ = g ( ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ = ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ - ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ( ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ( x ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ ) ${\$ x $=g(x)=x-{\frac {f(x)}{f'($ ${\textstyle f(x)/f'(x)=0.}$ ${\textstyle x=g(x)=x-{\frac {f(x)}{f'(x)}}}$ 따라서 ${\textstyle f(x)/f'(x)=0.}$ ( ${\textstyle f(x)/f'(x)=0.}$ ) ${\textstyle f(x)/f'(x)=0.}$ / ${\textstyle f(x)/f'(x)=0.}$ x ${\textstyle f(x)/f'(x)=0.}$ = 0 ${\textstyle f(x)/f'(x)=0.}$ ${\textstyle$ f $(f)/f'$ x $)=0$ )=0). $}$
모든 것의 역수는 0이 아니므로 $f (x)$ = $0$ : $x$ 는 $f$ 의 루트다. 바나흐 고정점 정리의 가정 하에서, 고정점 방법으로 액자에 넣은 뉴턴 반복은 선형 수렴을 나타낸다. 그러나 보다 상세한 분석에서는 특정한 ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ 에서 ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ n - ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ < ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ ${\$ 과 ${\textstyle |x_{n}-x|<Cq^{2^{n}}}$ 와) 같은 2차 정합성이 나타난다.
핼리의 방법은 올바르게 동작할 때 뉴턴의 방법과 유사하지만, 그 $|x_{n}-x|<Cq^{3^{n}}$ 는 $|x_{n}-x|<Cq^{3^{n}}$ n - $|x_{n}-x|<Cq^{3^{n}}$ < $|x_{n}-x|<Cq^{3^{n}}$ $|x_{n}-x|<Cq^{3^{n}}$ 3 n ${\$ 큐빅 컨버전스)이다. 일반적으로 $k\in \mathbb {N}$ $k\in \mathbb {N}$ $k\in \mathbb {N}$ N ${\$ 에 대해서도 $Cq^{k^{n}}$ 속도 $Cq^{k^{n}}$ $Cq^{k^{n}}$ $Cq^{k^{n}}$ ${\$ displaystyle $Cq^{k^{n}}}}$ 과(와) 융합하는 방법을 설계할 수 있다 $k\in \mathbb {N}$ 일반적으로 $k$ 가 높을수록 안정성이 떨어지고, 연산적으로도 비싸진다. 이러한 이유로, 일반적으로 고차방법은 사용되지 않는다.
Runge-Kutta 방법과 수치 일반 미분 방정식 해결기는 일반적으로 고정점 반복으로 볼 수 있다. 실제로, ODE 해결사의 A-안정성을 분석할 때 핵심 아이디어는 특수한 $y'=ay$ y $y'=ay$ = $y'=ay$ {\ $displaystyle$ $y$ $'=ay$ 부터 시작하는 $a$ 으로, $a$ 서{\ $displaystyle$ a}은 $a$ (는) 복합적인 숫자로서, ${\displaystyle$ a $}$ 의 실제 부분이 $y=0$ $고정점$ y $y=0$ = $y=0$ ${\displaysty y=0$ }에 수렴되는지 확인하는 것이다. ${}$ 은 $a$ (는) 음수다.^[a]
보통의 미분방정식이 해답을 가지고 있음을 보여주는 피카르-린델뢰프 정리는 본질적으로 바나흐 고정점 정리를 고정점 반복을 형성하는 함수의 특별한 순서에 적용하여 방정식에 대한 해답을 구성한다. 이러한 방식으로 ODE를 해결하는 것을 Picard 반복, Picard의 방법 또는 Picard 반복 과정이라고 한다.
엑셀의 반복 기능은 콜브룩 방정식의 솔루션을 15개의 유의미한 숫자의 정확도로 찾는 데 사용할 수 있다.^[1]^[2]
벨먼의 기능 방정식을 풀기 위해 동적 프로그래밍에 사용되는 "성공 근사" 체계 중 일부는 복귀함수의 공간에서 고정점 반복에 기초한다.^[3]^[4]

수축

실제 값과 함께 실제 라인에 정의된 $f$ 함수 $f$ $f$ 이(가) 립스키츠 $L<1$ L $L<1$ < $L<1$ $L<1$ 과 $L<1$ 와) 연속된 립스키츠라면, 이 함수는 정확히 하나의 고정점을 가지며, 고정점 반복은 어떤 초기 추측 $x_{0}.$ $x_{0}.$ ${\displaystystyle x_{0}$ 을 위해 그 고정점으로 수렴한다. $}}$ 이 $x_{0}.$ 정리는 어떤 완전한 메트릭스 공간으로 일반화할 수 있다.

이 정리의 증거:

$f$ $f$ 은 $f$ Lipschitz 상수 $L<1$ < 1 $L<1$ 을(를) 사용하여 Lipschitz 연속이므로 $\{x_{n},n=0,1,2,\ldots \}$ { $\{x_{n},n=0,1,2,\ldots \}$ $\{x_{n},n=0,1,2,\ldots \}$ = 0 $\{x_{n},n=0,1,2,\ldots \}$ $\{x_{n},n=0,1,2,\ldots \}$ , $\{x_{n},n=0,1,2,\ldots \}$ , $…}$ {\ $displaysty$ \{ $x_},n=0,$ 1,2 $,\ldots$ \}} 순서에 대해 다음이 있다 $\{x_{n},n=0,1,2,\ldots \}$

{\begin{aligned} x_{2}-x_{1} = f(x_{1})-f(x_{0}) &\leq L x_{1}-x_{0} ,\\ x_{3}-x_{2} = f(x_{2})-f(x_{1}) &\leq L x_{2}-x_{1} ,\\&\,\,\,\vdots \ \ \ {\text{and}}\\ x_{n}-x_{n-1} = f(x_{n-1})-f(x_{n-2}) &\leq L x_{n-1}-x_{n-2} .\end{aligned}}

위의 불평등 산출물을 조합하면 다음과 같다.

x_{n}-x_{n-1} \leq L^{n-1} x_{1}-x_{0} .

$L<1$ < $L<1$ $L<1$ 이후 $L<1$ L $L^{n-1}\rightarrow 0$ - 1 $L^{n-1}\rightarrow 0$ → $L^{n-1}\rightarrow 0$ $[\displaystyle L^{n-1}\오른쪽$ 화살표 $0}$ 을 $L^{n-1}\rightarrow 0$ (를) $n\rightarrow \infty .$ → $【\displaystyle n\오른쪽$ 화살표 $\inft$ .}

따라서 { $\{x_{n}\}$ $\{x_{n}\}$ $\{x_{n}\}\}$ 은 $\{x_{n}\}$ (는) Cauchy 시퀀스로, 따라서 $x^{*}$ x $x^{*}$ {\ $displaystyle$ x $^{*}}$ 로 수렴된다 $x^{*}$

반복 $x_{n}=f(x_{n-1})$ $x_{n}=f(x_{n-1})$ = f $x_{n}=f(x_{n-1})$ ( $x_{n}=f(x_{n-1})$ n $x_{n}=f(x_{n-1})$ - $x_{n}=f(x_{n-1})$ ) ${\displaystyle x_{n}=f(x_{n-1})$ 의 경우 $x_{n}=f(x_{n-1})$ $n$ ${\$ displaystyle $n}$ 이( $x^{*}=f(x^{*})$ ) 방정식의 양쪽에서 무한대로 가도록 $n$ 하고, $x^{*}=f(x^{*})$ = $f$ ( x $){*}=f(x^{*}})$ 를 얻는다 $x^{*}=f(x^{*})$ 이를 $x^{*}$ x ${{\$ 가 $x^{*}$ f{\ $displaystyle f$ }의 고정점임을 알 수 있다 $f$ 그래서 우리는 반복이 결국 고정점으로 수렴될 것임을 증명했다.

이 특성은 모든 반복이 수렴 고정점에 도달할 수 없기 때문에 매우 유용하다. 고정점 반복을 구성할 때, 그것이 수렴되도록 하는 것이 매우 중요하다. 고정점의 존재를 보증하는 고정점 이론이 몇 가지 있지만, 반복함수가 연속적이기 때문에 우리는 대개 위의 정리를 사용하여 반복이 수렴되는지 여부를 시험할 수 있다. 미터법 공간을 완성하기 위한 일반화된 정리의 증명도 비슷하다.

수렴가속

반복 시퀀스의 수렴 속도는 아이트켄의 델타 제곱 공정과 같은 수렴 가속법을 사용하여 높일 수 있다. 에이트켄의 방식을 고정점 반복에 적용하는 것을 스테펜센의 방법이라고 하며, 스테펜센의 방법으로는 적어도 2차적인 수렴 속도를 산출한다는 것을 알 수 있다.

참고 항목

참조

^ 또한 이 항목의 범위를 벗어난 장기간 이행을 계속하는 경우 특정 반복 A-안정성을 고려할 수 있다.

^ M A 쿠마르(2010), 워크시트 내에서 암묵적 방정식(Colebrook) 해결, 공간 생성, ISBN 1-4528-1619-0
^ Brkic, Dejan (2017) Excel을 이용한 흐름 마찰에 대한 Implicid Colebrook 방정식의 솔루션, 교육용 스프레드시트(eJSiE): 제10권: Iss. 2, 제2조 https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel에서 이용 가능:
^ 벨만, R. (1957) 프린스턴 대학 출판부의 동적 프로그래밍.
^ 스니도비치, M. (2010) 동적 프로그래밍: Foundation and Principles, Taylor와 Francis.

추가 읽기

Burden, Richard L.; Faires, J. Douglas (1985). "Fixed-Point Iteration". Numerical Analysis (Third ed.). PWS Publishers. ISBN 0-87150-857-5.
Hoffman, Joe D.; Frankel, Steven (2001). "Fixed-Point Iteration". Numerical Methods for Engineers and Scientists (Second ed.). New York: CRC Press. pp. 141–145. ISBN 0-8247-0443-6.
Judd, Kenneth L. (1998). "Fixed-Point Iteration". Numerical Methods in Economics. Cambridge: MIT Press. pp. 165–167. ISBN 0-262-10071-1.

외부 링크

[1] 또한 이 항목의 범위를 벗어난 장기간 이행을 계속하는 경우 특정 반복 A-안정성을 고려할 수 있다.

[2] M A 쿠마르(2010), 워크시트 내에서 암묵적 방정식(Colebrook) 해결, 공간 생성, ISBN 1-4528-1619-0

[3] Brkic, Dejan (2017) Excel을 이용한 흐름 마찰에 대한 Implicid Colebrook 방정식의 솔루션, 교육용 스프레드시트(eJSiE): 제10권: Iss. 2, 제2조 https://sie.scholasticahq.com/article/4663-solution-of-the-implicit-colebrook-equation-for-flow-friction-using-excel에서 이용 가능:

[4] 벨만, R. (1957) 프린스턴 대학 출판부의 동적 프로그래밍.

[5] 스니도비치, M. (2010) 동적 프로그래밍: Foundation and Principles, Taylor와 Francis.

[a]

[1]

[2]

[3]

[4]

Search

고정점 반복

네임스페이스

더

목차

예

적용들

수축

수렴가속

참고 항목

참조

추가 읽기

외부 링크