학장번호

Dean number(De)는 유체역학에서 차원이 없는 그룹으로, 곡선 파이프와 채널의 흐름 연구에서 발생한다. 그것은 영국 과학자 W. R. Dean의 이름을 따서 명명되었는데, 그는 직선 파이프 안의 푸아세유 흐름에서 아주 작은 곡선의 파이프에 이르는 섭동 절차를 이용하여 층류 흐름을 위한 곡선 파이프를 통한 유체 운동의 이론적 해결책을 제공했다.^[1][2]

물리적 컨텍스트

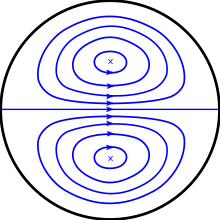
만약 유체가 어떤 지점이 곡선이 된 후 직선 파이프를 따라 움직이고 있다면, 굴곡부의 구심력은 유체 입자들의 주된 운동 방향을 바꾸게 할 것이다. 압력 증가와 함께 곡률에서 발생하는 역압 구배가 있어 볼록벽에 가까운 속도가 감소하며 파이프 외측을 향해 반대 현상이 발생한다. 이는 1차 흐름에 중첩된 2차 운동을 유발하며, 파이프 중심부의 유체는 커브 바깥쪽을 향해 쓸려가고 파이프 벽 근처의 유체는 커브 안쪽을 향해 되돌아간다. 이 2차 운동은 딘 vortices라고 불리는 역회전 세포의 한 쌍으로 나타날 것으로 예상된다.

정의

Dean 번호는 일반적으로 De(또는 Dn)로 표시된다. 파이프 또는 튜브의 흐름은 다음과 같이 정의된다.

${\displaystyle {\mathit {De}}={\frac {\sqrt {{\frac {1}{2}}\,({\text{inertial forces}})({\text{centripetal forces}})}}{\text{viscous forces}}}={\frac {\sqrt {{\frac {1}{2}}\,(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{D}})(\rho \,D^{2}\,R_{c}\,{\frac {v^{2}}{R_{c}}})}}{\mu {\frac {v}{D}}D\,R_{c}}}={\frac {\rho \,D\,v}{\mu }}{\sqrt {\frac {D}{2\,R_{c}}}}={\textit{Re}\,{\sqrt {\frac {D}{2\,R_{c}}}}}$

어디에

• ${\displaystyle \rho }$ ${\displaystyle \rho}$은(는) 유체의 밀도
• $[\displaystyle \mu }$은(는) 동적 점도
• ${\displaystyle v}$ ${\displaystyle v}$은(는) 축속 척도
• ${\displaystyle D}$ ${\displaystyle D}$은 직경(비원형 기하학의 경우 등가 직경이 사용됨. 레이놀즈 번호 참조)
• ${\displaystyle R_{}}$ ${\displaystyle c_{}}$ ${\$는 채널 경로의 곡률 반지름이다.
• ${\displaystyle \mathit{\text{Re}}}$ ${\$이(가) 레이놀즈 번호임.

따라서 Dean 번호는 레이놀즈 번호의 산물(직경 $D{\displaystyle }$ ${\displaystyle D}$ 파이프를 통한$$ 축류 $v{\displaystyle }$ ${\displaystyle v}$에 기초함$)$이며 곡률비의 제곱근이다.

난류 전이

이 흐름은 낮은 Dean 번호(De < 40~60)에 대해 완전히 단방향이다. 딘 수가 40~60~64~75년 사이에 증가함에 따라, 단면에서 일부 파동 섭동을 관찰할 수 있으며, 이는 어느 정도 이차적인 흐름을 증명한다. 그것(De > 64~75)보다 더 높은 Dean 번호에서 Dean vortices 쌍은 안정적이 되어 1차적인 동적 불안정성을 나타낸다. De > 75~200에 대해 2차 불안정성이 나타나는데, 여기서 vortices는 굴절, 비틀림, 그리고 결국 병합 및 쌍 분할을 나타낸다. De > 400에 대한 완전한 난류 흐름 형성.^[3] 층류에서 난류 흐름으로의 전환도 여러 연구에서 조사되었는데, 이는 파라미터가 곡률비에 크게 의존하기 때문에 보편적인 해결책이 존재하지 않는다.^[4] 다소 뜻밖에도 곡면성이 불안정성을 유발하는 것으로 알려져 있음에도 불구하고, 층류 흐름은 직선 파이프보다 더 큰 레이놀즈 수(연구된 가장 높은 곡률 비율의 경우 2배수까지)에 대해 유지될 수 있다.^[5]

더 딘 방정식

Dean 번호는 소위 Dean 방정식에 나타난다.^[6] 이것은 전체 Navier에 대한 근사치 입니다.–토로이드 파이프에서 뉴턴 유체의 일정한 축 균일한 흐름을 위한 방정식, 선행 순서 곡률 효과(즉${\displaystyle ,}$ /${\displaystyle r}$ ${\displaystyle \ll }$ ${\displaystyle 1}$ ${\displaystyle a/r\ll$ 1$}$에 대한 선행 순서 방정식)를 유지함으로써 얻는다.$$

We use orthogonal coordinates ${\displaystyle (x,y,z)}$ with corresponding unit vectors ${\displaystyle ({\hat {\boldsymbol {x}}},{\hat {\boldsymbol {y}}},{\hat {\boldsymbol {z}}})}$ aligned with the centre-line of the pipe at each point. 축방향은 $z{\displaystyle \stackrel{}{\mathit{}}}$^$${\$displaystyle${\$hat${\$boldsymbol{z$이고,${\displaystyle \stackrel{}{}}$x$^$ {\$displaystyle$ {\$boldsymbol$ {x$}}}$은(는) 중심선의 평면에서 $정상$이고${\displaystyle \stackrel{}{}}$y$$^ {\$displaystystyle {\hat{\bmbol{y}}}}}}}}}}}}}}}}}}$은(는 바이노말이다. For an axial flow driven by a pressure gradient ${\displaystyle G}$, the axial velocity ${\displaystyle u_{z}}$ is scaled with ${\displaystyle U=Ga^{2}/\mu }$. The cross-stream velocities ${\displaystyle u_{x},u_{y}}$ are scaled with ${\displayst$$yle (a/R)^{1/2}U$ ${\displaystyle {그리고\mathrm{}}^{}}$ ${\displaystyle U}$ 2${\displaystyle {}^{}}$/ ${\displaystyle L}$ ${\displaystyle \rho aU^{2}/L}$과(와) 교차 스트림 압력$.$ 길이는 튜브 반지름 $a{\displaystyle }$ ${\\displaystyle$ a$}$에 따라 크기가 조정된다$.$

이러한 비차원적 변수와 좌표로 볼 때, Dean 방정식은 그 다음이다.

${\displaystyle De\left({\frac {\mathrm {D} u_{x}}{{D} t}-u_{z}^{2}\오른쪽)=-De{\frac {\partial p}{\partial x}+\nabla ^{2}u_{x}}}}}}$

${\displaystyle De{\frac {\mathrm {D} u_{y}}{\mathrm {D}t}=-De{\frac {\partial p}{\partial y}+\nabla^{2}u_{y}}}}}$

${\displaystyle De{\frac {\mathrm {D} u_{z}}{\mathrm {D} t}=1+\nabla ^{2}u_{z}}}}$

${\displaystyle {\frac {\fract u_{x}}{\frac x}+{\fract u_{y}}{\frac y}=0}$

어디에

${\displaystyle {\frac {\mathrm {D}{\mathrm {D} t}=u_{x}{\frac {\partial x}+u_{y}{\frac {\partial y}}}}}$

대류파생이다.

Dean number De는 시스템에 남아 있는 유일한 파라미터로 선행 순서 곡률 효과를 캡슐화한다. 고차 근사치에는 추가 매개변수가 포함된다.

약한 곡률 효과(Small De)의 경우 Dean 방정식은 De에서 연속적인 확장으로 해결할 수 있다. 선행 축방향 Poiseuille 흐름에 대한 첫 번째 보정은 중앙을 가로지르는 곡선 안쪽에서 바깥쪽으로 그리고 가장자리를 중심으로 뒤쪽까지 흐름을 전달하는 단면 내 한 쌍의 vorticled-order Axial Poiseuille flows. 이 솔루션은 중요한 Dean 번호 D $e{\displaystyle }$ ${\displaystyle c_{}}$ ${\displaystyle {}_{}}$ $(\displaystyle De_{c}\$ 약 $956})$까지 안정적이다$.$^[7] 더 큰 De의 경우 여러 솔루션이 있는데, 대부분은 불안정하다.

누셀트 수와의 관계

${\displaystyle Nu=0.76\cdot Re^{-0.23}\cdot De^{-0.114}}$

여기서:

• 레이놀즈 수
• De is Dean Number
• 누는 누셀트 수

참조

추가 읽기

• Berger, S. A.; Talbot, L.; Yao, L. S. (1983). "Flow in Curved Pipes". Annu. Rev. Fluid Mech. 15: 461–512. Bibcode:1983AnRFM..15..461B. doi:10.1146/annurev.fl.15.010183.002333.