압축 흐름

압축성 흐름(또는 가스 역학)은 유체 밀도에 큰 변화가 있는 흐름을 다루는 유체 역학 분야입니다.모든 흐름은 압축 가능하지만 마하 수(흐름 속도와 음속의 비율)가 0.3보다 작을 경우 흐름은 압축 불가능으로 취급됩니다(^[1]이 경우 속도에 의한 밀도 변화가 약 5%이기 때문입니다).압축성 흐름에 대한 연구는 고속 항공기, 제트 엔진, 로켓 모터, 행성 대기권 진입, 가스 파이프라인, 연마재 블라스팅과 같은 상업적 용도 및 기타 많은 분야에 관련된다.

역사

가스 역학 연구는 종종 현대 고속 항공기의 비행과 우주 탐사 차량의 대기권 재진입과 관련이 있다. 그러나 그 기원은 단순한 기계에서 비롯된다.19세기 초, 발사된 총알의 동작에 대한 조사는 ^[2]총과 포의 정확성과 능력의 향상으로 이어졌다.세기가 지나면서, 구스타프 드 라발과 같은 발명가들은 이 분야를 발전시켰고, 에른스트 마하와 같은 연구원들은 실험을 통해 관련된 물리적 현상을 이해하려고 했다.

20세기 초에 가스 역학 연구의 초점은 결국 항공우주 산업이 될 것으로 옮겨갔다.루드비히 프란틀과 그의 학생들은 경계층에서 초음속 충격파, 초음속 풍동, 초음속 ^[2]노즐 설계에 이르는 중요한 개념을 제안했다.프란틀의 학생인 테오도르 폰 카르만은 초음속 흐름에 대한 이해를 계속 향상시켰다.다른 주목할 만한 인물들(마이어, 루이지 크로코 [it], 애셔 샤피로)도 현대 가스 역학의 기초가 되는 원리에 크게 기여했다.많은 다른 사람들도 이 분야에 기여했습니다.

20세기 초 가스 역학에 대한 개념적 이해의 향상과 함께 흔히 "음향 장벽"이라고 불리는 항공기의 도달 가능한 속도에 장벽이 존재한다는 대중의 오해가 있었다.사실 초음속 비행의 장벽은 극복해야 할 완고한 장벽이었지만 기술적인 장벽에 불과했다.다른 요인들 중에서, 기존의 에어로포일은 흐름이 음속에 가까워질 때 드래그 계수가 극적으로 증가했습니다.더 큰 저항을 극복하는 것은 현대적 디자인으로 입증되었고, 따라서 음향 장벽에 대한 인식은 어려웠다.그러나 항공기 설계는 Bell X-1을 생산할 정도로 충분히 진전되었다.척 예거가 조종한 X-1은 1947년 ^[3]10월 공식적으로 초음속을 달성했다.

역사적으로 가스 역학 지식을 강화하기 위해 두 가지 평행한 연구 경로를 따라왔다.실험 가스 역학에서는 발견을 문서화하기 위한 광학 기술을 사용하여 충격관 및 탄도 범위에서의 풍동 모델 실험 및 실험을 수행합니다.이론적인 가스 역학에서는 가변 밀도 가스에 적용되는 운동 방정식과 그 해법을 고려합니다.기본적인 기체 역학의 대부분은 분석적이지만, 현대의 계산 유체 역학은 특정 기하학적 구조와 흐름 특성에 대해 압축 가능한 흐름의 다루기 어려운 비선형 편미분 방정식을 해결하기 위해 계산 능력을 적용합니다.

입문 개념

압축 흐름의 기본 이론에는 몇 가지 중요한 가정이 포함되어 있습니다.모든 유체는 분자로 구성되어 있지만 흐름에서 엄청난 수의 개별 분자를 추적할 필요가 없습니다(예: 대기압).대신 연속체 가정은 낮은 밀도를 제외한 연속적인 물질로 흐르는 가스를 고려할 수 있게 한다.이 가정은 대부분의 가스-동적 문제에 대해 정확한 대폭적인 단순화를 제공합니다.희소가스 역학이라는 저밀도 영역에서만 개별 분자의 움직임이 중요해집니다.

관련된 가정은 고체 표면에서의 유속이 표면 자체의 속도와 동일하다고 가정되는 미끄럼 방지 조건이며, 이는 연속체 흐름을 가정한 직접적인 결과이다.미끄럼 방지 조건은 흐름이 점성이라는 것을 의미하며, 그 결과 저속 흐름과 마찬가지로 공기를 통해 고속으로 이동하는 물체에 경계층이 형성됩니다.

압축할 수 없는 흐름의 대부분의 문제는 두 가지 미지의 것, 즉 압력과 속도만을 수반합니다. 압력과 속도는 일반적으로 유체 밀도를 일정하게 가정한 상태에서 질량과 선형 운동량의 보존을 설명하는 두 가지 방정식을 풀어서 발견됩니다.그러나 압축 가능한 흐름에서는 가스 밀도와 온도도 변수가 됩니다.압축 흐름 문제를 해결하기 위해서는 기체에 대한 상태 방정식과 에너지 방정식의 보존이라는 두 가지 방정식이 더 필요합니다.대부분의 가스-동적 문제의 경우, 간단한 이상 기체 법칙이 적절한 상태 방정식입니다.

유체 역학 문제는 라그랑지앙과 오일러로 불리는 두 가지 유형의 참조 프레임을 가지고 있습니다.라그랑지안 접근법은 유동장을 통과할 때 고정된 동일성의 유체 질량을 따릅니다.반면, 오일러식 기준 프레임은 유체와 함께 움직이지 않습니다.오히려 액체가 흐르는 고정 프레임 또는 제어 볼륨입니다.오일러 프레임은 대부분의 압축 흐름 문제에서 가장 유용하지만, 운동 방정식은 호환 가능한 형식으로 작성되어야 합니다.

마지막으로 공간은 3차원을 갖는 것으로 알려져 있지만, 1차원의 공간만 중요한 경우에는 기체역학을 수학적으로 설명하는 데 있어 중요한 단순화를 얻을 수 있으므로 1차원 흐름을 가정한다.이는 흐름 특성이 흐름에 수직이 아닌 흐름 방향으로 주로 변화하는 덕트, 노즐 및 확산기 흐름에서 잘 작동합니다.그러나 고속으로 이동하는 물체 위를 흐르는 외부 흐름을 포함한 압축 가능한 흐름의 중요한 클래스는 적어도 2차원 처리가 필요합니다.3가지 공간 차원과 시간 차원이 모두 중요한 경우, 우리는 종종 지배 방정식의 컴퓨터화된 해법에 의존합니다.

마하 수, 파동 및 음속

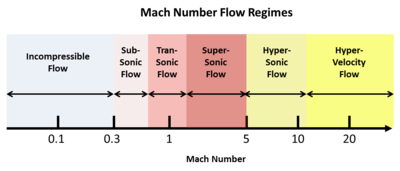
마하수(M)는 음속에 대한 물체(또는 흐름)의 속도의 비율로 정의됩니다.예를 들어, 상온에서 음속은 약 340m/s(1,100ft/s)입니다.M의 범위는 0 ~0 이지만, 이 넓은 범위는 자연스럽게 여러 흐름으로 분류됩니다.아음속, 천음속, 초음속, 극초음속, 초고속 흐름입니다.다음 그림은 이들 흐름의 마하 수치 "스펙트럼"을 나타내고 있습니다.

이러한 흐름 방식은 임의로 선택되는 것이 아니라 압축 가능한 흐름의 기초가 되는 강력한 수학적 배경에서 자연스럽게 발생한다(인용된 참조 교과서 참조).매우 느린 흐름 속도에서는 소리의 속도가 너무 빨라서 수학적으로 무시되고 마하 수치는 관련이 없습니다.그러나 흐름 속도가 음속에 가까워지면 마하 수치가 중요해지고 충격파가 나타나기 시작합니다.따라서 트랜조닉 체제는 다른(그리고 훨씬 더 복잡한) 수학적 처리에 의해 설명된다.초음속에서는 흐름은 마하각과 유사한 경사각도의 파동운동에 의해 지배된다.마하 5 이상에서는 이러한 파각은 너무 작기 때문에 다른 수학적 접근이 필요하며, 극초음속 속도를 정의한다.마지막으로, 수 km/s 범위에서 행성 대기권 진입과 비슷한 속도에서, 소리의 속도는 현재 매우 느려서, 다시 한번 고속화 체제에서 수학적으로 무시된다.

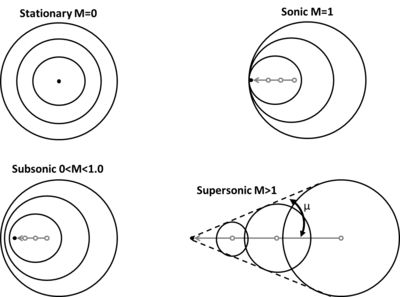
물체가 기체 내에서 아음속에서 초음속으로 가속할 때, 다양한 종류의 파동 현상이 발생한다.이러한 변화를 설명하기 위해 다음 그림은 대칭 음파를 방출하는 정지점(M = 0)을 보여준다.소리의 속도는 균일한 유체 안에서 모든 방향에서 동일하기 때문에, 이러한 파장은 단순히 동심원구입니다.음 발생점이 가속하기 시작하면 음파는 운동 방향으로 '뚝'하고 반대 방향으로 '뚝' 뻗는다.포인트가 음속(M = 1)에 도달하면 발생하는 음파와 동일한 속도로 이동합니다.따라서 무한히 많은 음파가 점보다 앞서 "확대"되어 충격파를 형성합니다.초음속 흐름에 도달하면 입자는 음파를 계속 남길 정도로 빠르게 움직이고 있다.이 경우 점 뒤에 이어지는 이러한 파형의 궤적은 마하 파형 각도 또는 마하 각도, μ:

$({displaystyle \mu =\arcsin \leftfrac {a}{V}}\right)=\arcsin \leftfrac {1}{M}\right)}$

$여기$서$$\$displaystyle$a는 기체 내 음속을 $나타내고$ V$\displaystyle$V는 물체의 속도를 나타냅니다$$.비록 오스트리아의 물리학자 에른스트 마흐의 이름을 따서 명명되었지만, 이 사선파는 크리스티안 도플러에 ^[4]의해 처음 발견되었다.

일차원 흐름

1차원(1-D) 흐름은 흐름 매개변수가 하나의 공간 차원, 즉 덕트 길이에 따라 유의하게 변화하는 것으로 가정되는 덕트 또는 채널을 통과하는 가스 흐름을 말한다.1-D 채널 흐름을 분석할 때 다음과 같은 여러 가지 가정을 합니다.

• 덕트 길이 대 폭의 비(L/D)는 약 5개(마찰 및 열 전달을 무시하기 위해),
• 안정성과 불안정한 흐름,
• 흐름은 등엔트로픽(즉, 가역 단열 과정),
• 이상기체의 법칙(즉, P = δRT)

집속 분산 라발 노즐

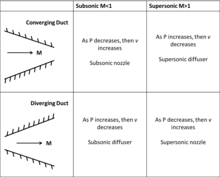
유속이 아음속에서 초음속으로 빨라짐에 따라 노즐과 디퓨저 흐름의 물리가 변화한다.유체 역학 및 열역학 보존 법칙을 사용하여 채널 흐름에 대한 다음과 같은 관계를 개발합니다(질량과 운동량 보존 조합).

$=$$$$A}}\right$

여기서 dP는 압력의 차분 변화, M은 마하 수, θ는 기체의 밀도, V는 흐름 속도, A는 덕트의 면적 변화, dA는 덕트의 면적 변화입니다.이 방정식은 아음속 흐름의 경우 수렴 덕트(dA < 0)는 흐름 속도를 증가시키고 발산 덕트(dA > 0)는 흐름 속도를 감소시킨다는 것을 나타냅니다.초음속 흐름의 경우 (1 - M²)의 부호 변화로 인해 그 반대가 발생하며, 수렴 덕트(dA < 0)는 흐름 속도를 감소시키고 발산 덕트(dA > 0)는 흐름 속도를 증가시킨다.마하 = 1에서 덕트 면적이 최대 또는 최소가 되어야 하는 특수한 경우가 발생합니다.실질적으로 마하 1 이상으로의 흐름을 가속할 수 있는 것은 최소 면적뿐입니다.서브 슈퍼바이저 디퓨저 및 노즐 표를 참조하십시오.

따라서 마하 1로의 흐름을 가속화하려면 노즐을 최소 단면적으로 수렴한 후 팽창하도록 설계해야 합니다.이 타입의 노즐, 즉 집속형 노즐은 그것을 발명한 구스타프 드 라발의 이름을 따서 드 라발 노즐이라고 불립니다.아음속 흐름이 수렴 덕트로 유입되어 면적이 감소하면 흐름이 가속됩니다.덕트의 최소 면적(노즐의 목구멍이라고도 함)에 도달하면 흐름은 마하 1에 도달할 수 있습니다.흐름의 속도가 계속 증가하려면 질량 보존을 준수하기 위해 밀도가 감소해야 합니다.이 밀도를 낮추려면 흐름이 확장되어야 하며, 그러기 위해서는 흐름이 분기 덕트를 통과해야 합니다.de Laval 노즐의 이미지를 참조하십시오.

기체의 최대 도달 속도

궁극적으로, 에너지 절약 법칙에 따라, 기체는 에너지 함량에 따라 일정한 최대 속도로 제한됩니다.기체가 도달할 수 있는 최대 속도 V는_max 다음과 같습니다.

${\displaystyle V_{\text{max}}=sqrt {2c_{p}T_{t}}}}:$

여기서_p c는 가스의 비열이고 T는_t 흐름의 정체 온도입니다.

등엔트로픽 흐름 마하 수 관계

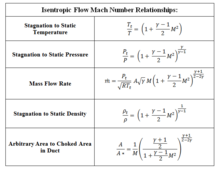
보수 법칙과 열역학을 사용하여 형태의 여러 관계

${\displaystyle {{\text{property}_{1}}{\text{property}_{2}}=f(M,\gamma)}$

얻을 수 있습니다.여기서 M은 마하 수치이고 θ는 특정 발열의 비율(공기의 경우 1.4)입니다).등엔트로픽 흐름 마하 수 관계 표를 참조하십시오.

초음속 흐름 실현

앞서 말한 바와 같이, 흐름이 초음속이 되기 위해서는 최소 면적의 덕트, 즉 소닉 인후를 통과해야 한다.또한 마하 1에 도달하기 위해서는 약 2의 압력비 P/P가_bt 필요하다.마하 1에 도달하면 목구멍의 흐름이 막힌다고 한다.다운스트림의 변화는 음속으로만 업스트림으로 이동할 수 있기 때문에 노즐을 통과하는 질량 흐름은 흐름이 막힌 후 다운스트림 상태의 변화에 영향을 받지 않습니다.

기체의 비등방성 1D 채널 흐름 - 정상 충격파

일반 충격파는 국소 흐름 방향에 수직인 충격파입니다.이러한 충격파는 압력파가 축적되어 운동 에너지를 열에너지로 변환하는 매우 얇은 충격파로 합쳐질 때 발생합니다.따라서 파동은 서로를 추월하고 보강하여 무한히 작은 일련의 음파로부터 유한 충격파를 형성합니다.충격에 걸친 상태 변화는 매우 돌이킬 수 없기 때문에 충격에 걸쳐 엔트로피가 증가합니다.정상적인 충격파를 분석할 때는 완벽한 기체의 1차원, 안정 및 단열 흐름을 가정한다.정체 온도와 정체 엔탈피는 충격의 상류와 하류에서 동일합니다.

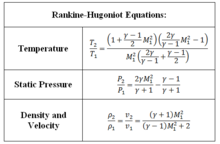
정상 충격파는 스탠딩 정상 충격과 이동 충격의 두 기준 프레임 중 하나로 쉽게 분석할 수 있습니다.일반 충격파 이전의 흐름은 초음속이어야 하며, 일반 충격 후의 흐름은 아음속이어야 한다.Rankine-Hugoniot 방정식은 흐름 조건을 해결하기 위해 사용됩니다.

2차원 흐름

1차원 흐름은 직접 분석할 수 있지만, 2차원 흐름의 특수한 사례에 불과합니다.따라서 1차원 흐름의 결정적인 현상 중 하나인 정상적인 충격도 마찬가지로 더 큰 종류의 경사 충격의 특수한 경우일 뿐입니다.또한 "정상"이라는 이름은 발생 빈도가 아닌 기하학에 관한 것입니다.비스듬한 충격은 항공기 흡입구 설계, 초음속 비행 물체, 그리고 (더 기본적인 수준에서) 초음속 노즐과 확산기와 같은 애플리케이션에서 훨씬 더 흔하다.유량 상태에 따라 활충격 형태로 유량에 사선충격을 부착하거나 유량에서 분리할 수 있다.

초음속 풍동 X-15 모델에 부착된 충격파

무딘 몸체에 대한 Bowshock

사선 충격파

사선 충격파는 일반 충격파와 유사하지만 흐름 방향과 90° 미만의 각도에서 발생합니다.0이 아닌 각도(θ)에서 흐름에 장애가 발생하면 흐름은 변화하는 경계 조건에 응답해야 합니다.따라서 비스듬한 충격이 형성되어 흐름의 방향이 변화합니다.

충격 극성 다이어그램

또, 흐름 편향 레벨(θ)에 근거해, 사선 충격은 강하거나 약한 것이 특징이다.강한 충격은 충격 전체에 걸쳐 더 큰 편향과 더 많은 엔트로피 손실을 특징으로 하며, 약한 충격은 그 반대이다.이러한 충격의 차이를 대략적으로 이해하기 위해 충격 극 다이어그램을 사용할 수 있습니다.충격 후의 정적 온도 T*에서는 충격 후의 음속은 다음과 같이 정의됩니다.

${\displaystyle A^{*}=\sqrt {\displaystyle RT^{*}}}$

R을 기체 상수로 하고 δ를 비열비로 한다.마하 수치는 데카르트 좌표로 분할할 수 있습니다.

${\displaystyle {begin { aligned} M_{2x}^{*}&=frac {V_{x} {a^{*}}\M_{2y}^*}&=frac {V_{y}}{\end{aligned}}}}$

유체 속도 V의 x 및 y 성분으로 V와 V를_y 사용한다_x.충격 전 마하 수치를 사용하여 조건의 궤적을 지정할 수 있습니다.일부_max trans에서는 흐름이 강한 경사 충격에서 약한 경사 충격으로 전환됩니다.θ = 0°일 때 강한 경사 충격 한계에서 정상적인 충격이 발생하고 약한 충격파 한계에서 마하파가 발생한다.

경사 충격 반사

충격의 기울기로 인해 경사 충격이 발생한 후, 아래에 설명하는 세 가지 다른 방식으로 경계와 상호작용할 수 있습니다.

입체 경계

유입 흐름은 처음에 흐름에 대해 각도θ만큼 회전한다.이 충격파는 고체 경계에서 반사되어 흐름은 – to만큼 회전하여 경계와 다시 평행하게 됩니다.각 진행성 충격파는 더 약하고 각도는 증가한다는 점에 유의해야 합니다.

불규칙반사

불규칙한 반사는 위에서 설명한 경우와 매우 유사하며, θ가 최대 허용 회전각보다 크다는 주의사항이 있습니다.따라서 분리된 충격이 형성되고 마하 반사로 알려진 더 복잡한 반사가 발생합니다.

프란틀-마이어 팬

프란틀-마이어 팬은 압축 팬과 확장 팬으로 표현할 수 있습니다.또한 프란틀-마이어 팬은 경계층(흐름 및 고체)을 통과하여 다른 변화에도 반응합니다.충격파가 단단한 표면에 닿으면 팬은 반대 패밀리의 팬으로 돌아오고, 한쪽이 자유 경계에 닿으면 팬은 반대 타입의 팬으로 돌아옵니다.

프란틀-마이어 확장 팬

지금까지 논의된 유일한 흐름 현상은 흐름을 느리게 하고 엔트로피를 증가시키는 충격파입니다.루드비히 프란틀과 테오도르 마이어의 이름을 딴, 이른바 '프란틀-마이어 팽창 팬'에서 초음속 흐름을 가속할 수 있다.확장 메커니즘은 다음 그림에 나와 있습니다.

경사진 장애물을 만나 경사충격을 형성하는 흐름과는 반대로 일련의 등엔트로픽 마하파를 통해 볼록한 모서리를 중심으로 팽창하고 팽창팬을 형성한다.팽창 "팬"은 초기 마하 각도에서 최종 마하 각도에 이르는 마하 파동으로 구성됩니다.마하수의 증가는 통로의 볼록한 각도(θ)에만 비례하므로 날카로운 모서리 또는 둥근 모서리 둘 다로 흐름이 확장될 수 있다.Prandtl-Meyer 팬을 생성하는 확장 코너는 날카롭거나(그림과 같이), 둥글게 할 수 있습니다.Total Turning 각도가 같으면 P-M flow 용액도 같습니다.

프란틀-마이어 팽창은 라발 노즐의 작동에 대한 물리적 설명으로 볼 수 있습니다.노즐의 윤곽은 부드럽고 연속적인 일련의 프랜드틀-마이어 팽창파를 생성합니다.

프란틀-마이어 압축팬

프랜드틀-마이어 압축은 프랜드틀-마이어 확장과 반대되는 현상입니다.서서히 θ의 각도로 흐르면 압축팬을 형성할 수 있다.이 선풍기는 일련의 마하파이며 결국 사선 충격으로 합쳐집니다.흐름은 등엔트로픽 영역(팬을 통과하는 흐름)과 비등엔트로픽 영역(사선 충격을 통과하는 흐름)에 의해 정의되므로 두 흐름 영역 사이에 슬립 라인이 발생합니다.

적용들

초음속 풍동

초음속 바람 터널은 마하 1.2에서 5 사이의 대략적인 마하 범위를 넘는 초음속 흐름의 시험과 연구에 사용된다.풍동 이면의 작동 원리는 상류에서 하류로 큰 압력 차이가 유지되어 흐름을 주도한다는 것입니다.

풍동(風洞)은 연속 작동 풍동(風洞)과 간헐 작동 풍동(風洞)의 두 가지 범주로 나눌 수 있다.연속적으로 작동하는 초음속 풍동에는 테스트 섹션의 크기에 따라 급격히 증가하는 독립적인 전력원이 필요합니다.간헐적인 초음속 풍동은 장시간 전기 에너지를 저장하고 일련의 간단한 테스트를 통해 에너지를 방출한다는 점에서 비용이 적게 든다.이 두 가지 차이는 배터리와 콘덴서의 비교와 유사합니다.

초음속 풍동 도식

랭글리 유도 초음속 풍동 진공구

블로 다운형 초음속 풍동에서는 레이놀즈 수치가 높고 저장 탱크가 작으며 건조한 공기를 쉽게 사용할 수 있습니다.그러나 고압의 위험을 초래하고 고정압을 유지하는 데 어려움을 겪으며 작동 중에 소음이 발생합니다.

유입 초음속 풍동은 압력 위험과 관련이 없고 일정한 정체 압력을 허용하며 비교적 조용하다.불행히도 레이놀즈 흐름의 수에 대한 범위가 한정되어 있어 큰 진공 탱크가 필요합니다.

초음속 풍동에서의 연구와 테스트를 통해 지식을 얻는다는 것에는 이견이 없다. 하지만, 그 시설은 종종 시험 조건에 필요한 큰 압력비를 유지하기 위해 엄청난 양의 전력을 필요로 한다.예를 들어, 아놀드 엔지니어링 개발 단지는 세계에서 가장 큰 초음속 풍동을 가지고 있으며 작은 도시를 작동시키기 위해 필요한 전력을 필요로 한다.이러한 이유로 대학에서는 대형 풍동이 흔하지 않게 되었다.

초음속 항공기 입구

아마도 비스듬한 충격의 가장 일반적인 요건은 마하 2 이상의 속도를 위한 초음속 항공기 입구일 것이다. (F-16은 최대 속도가 마하 2이지만 비스듬한 충격 흡입구가 필요하지 않다.)흡입구의 한 가지 목적은 유입되는 초음속 공기가 터보젯 엔진으로 들어가기 전에 아음속으로 감속하기 때문에 충격으로 인한 손실을 최소화하는 것입니다.이는 1개 이상의 경사 충격에 이어 업스트림 마하 수치가 보통 1.4 미만인 매우 약한 정상 충격에 의해 달성된다.흡기구를 통과하는 기류는 0에서 최대 초음속까지의 광범위한 속도 범위에서 올바르게 관리해야 합니다.이는 흡기 표면의 위치를 변경함으로써 이루어집니다.

이륙부터 마하 2를 초과하는 속도까지 허용 가능한 성능을 달성하기 위해 가변 기하학이 필요하지만 이를 달성할 수 있는 유일한 방법은 없다.예를 들어 최대 속도가 약 마하 3인 경우 XB-70은 램프 조절이 가능한 직사각형 인렛을, SR-71은 센터 콘 조절이 가능한 원형 인렛을 사용했습니다.

램프 포함 XB-70 직사각형 입구(보이지 않음)

SR-71 원형 입구(중앙 본체 포함)

「 」를 참조해 주세요.

• 압축할 수 없는 흐름
• 보존법
• 엔트로피
• 상태 방정식
• 가스 동력학
• 열용량비
• 등엔트로픽 노즐 흐름
• 흐름장의 라그랑지안과 오일러의 규격
• 프란틀-마이어 함수
• 열역학, 특히 "일반적으로 고려되는 열역학 프로세스" 및 "열역학 법칙"

레퍼런스

• Liepmann, Hans W.; Roshko, A. (1957) [1957]. Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0.
• Anderson, John D. Jr. (2003) [1982]. Modern Compressible Flow (3rd ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-242443-5.
• John, James E.; Keith, T. G. (2006) [1969]. Gas Dynamics (3rd ed.). Prentice Hall. ISBN 0-13-120668-0.
• Oosthuizen, Patrick H.; Carscallen, W. E. (2013) [1997]. Introduction to Compressible Flow (2nd ed.). CRC Press. ISBN 978-1439877913.
• Zucker, Robert D.; Biblarz, O. (2002) [1977]. Fundamentals of Gas Dynamics (2nd ed.). Wiley. ISBN 0471059676.
• Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press Company. ISBN 978-0-471-06691-0.
• Anderson, John D. Jr. (2000) [1989]. Hypersonic and High Temperature Gas Dynamics. AIAA. ISBN 1-56347-459-X.

외부 링크

• NASA 압축 공기역학 초보자 가이드
• 버지니아 공대 압축식 흐름 계산기
• [1]