복소 평면

수학에서 복소평면은 복소수에 의해 형성된 평면이며, 데카르트 좌표계는 실축이라 불리는 x축을 실수에 의해 형성하고, 허수축이라 불리는 y축을 허수에 의해 형성한다.

복소 평면을 사용하면 복소수를 기하학적으로 해석할 수 있습니다.또한 벡터처럼 추가됩니다.두 복소수의 곱은 극좌표로 더 쉽게 표현될 수 있다. 즉, 곱의 크기 또는 계수는 두 절대값의 곱이고, 곱의 각도 또는 인수는 두 개의 각도 또는 인수의 합이다.특히 복소수 계수 1에 의한 곱셈이 회전이 된다.

복소평면은 때때로 아르간드평면 또는 가우스평면으로 알려져 있다.

표기법

복소수

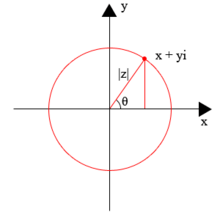
복소수 해석에서 복소수는 통상적으로 기호 z로 나타나며, 기호 z는 실(x) 부분과 허수(y) 부분으로 분리할 수 있다.

z=x+iy

예를 들어 z = 4 + 5i, 여기서 x와 y는 실수이고 i는 허수 단위입니다.이 관례 표기법에서 복소수 z는 데카르트 평면의 점(x, y)에 해당합니다.

데카르트 평면에서 점(x, y)은 다음과 같이 극좌표로 표현될 수 있다.

(x,y)=(r\cos \theta,r\sin \theta)\qquad (r,\theta)=\leftrt {x^{2}+y^{2}}}},\arctan(\frac {y}{x}}\right).

데카르트 평면에서 아크탄젠트는 -θ/2부터 θ/2까지(라디안 단위) 값을 취한다고 가정할 수 있으며, x 0 ^{[note 1]}0일 때 점(x, y)에 대해 보다 완전한 아크탄젠트 함수를 정의하기 위해 주의를 기울여야 한다.복합 평면에서 이러한 극좌표는 다음과 같은 형태를 취한다.

(\displaystyle z=x+iy=z \left(\cos \theta +i\sin \theta \오른쪽)=z e^{i\theta })

어디^{[note 2]}

z = displayrt {x^{2}+y^{2}}};\frac \theta =\frac(z)=frac {1}{i}}\ln {frac {z}=-i\ln {frac {z}{z}}}.

여기서 z는 복소수 z의 절대값 또는 계수이다. z의 인수인 θ는 보통 $구간$ 0 $\leq θ$ < 2 ;에서 취해지고, 마지막 등식(to^iθ z e)은 오일러의 공식에서 취해진다.복소수함수는 주기 2µi로 주기적이기 때문에 θ의 범위에 제약이 없으면 z의 인수는 다중값이다.따라서 θ가 arg(z)의 값 중 하나일 경우 다른 값은 arg( $z) = θ$ + $2n$ 으로 $지정$ 됩니다.여기서 n은 0이 아닌 ^[2]정수입니다.

복소수의 기하학적 뷰는 명시적으로 거의 사용되지 않지만, $복소수$ $w$ 와 z의 내부곱은 $\Re (w{\overline {z}})$ ( $\Re (w{\overline {z}})$ z $\Re (w{\overline {z}})$ δ $)\displaystyle \Re (w{\overline {z$ 에 의해 주어지는 차원 2의 유클리드 벡터 공간의 구조에 암묵적으로 기초한다. $복소수$ z의 $절대값$ 은 그 절대값과 일치한다.유클리드 노름과 그 $인수$ arg( $z)$ 는 각도가 1에서 $z$ 로 바뀐다.

등고선 통합 이론은 복잡한 분석의 주요 부분을 구성한다.이 맥락에서 닫힌 곡선 주위를 이동하는 방향은 중요합니다. 즉, 곡선이 횡단되는 방향을 반대로 하면 적분 값이 -1이 곱됩니다.관례상 양의 방향은 시계 반대 방향이다.예를 들어, z = 1 지점에서 시작한 후 z = i 지점을 통해 위쪽으로, 왼쪽으로 이동한 다음 -1 지점을 지나 아래쪽으로, -i 지점을 지나 -1 지점을 지나 아래쪽으로, 마지막으로 -i 지점을 지나 위쪽으로, 그리고 오른쪽으로 z = 1 지점을 지나 오른쪽으로 이동할 때 단위 원이 양의 방향으로 횡단됩니다.

거의 모든 복잡한 분석은 복잡한 함수, 즉 복잡한 평면의 일부 서브셋을 복잡한 평면의 다른(중복하거나 심지어 동일한) 서브셋에 매핑하는 함수와 관련이 있다.여기서 f(z)의 도메인은 z평면에 있다고 말하는 것이 관례이며, f(z)의 범위는 w평면의 포인트 세트라고 한다.기호로 쓰다

\displaystyle z=x+iy;\qquad f(z)=w=u+iv}

함수 f를 z 평면(좌표(x, y)에서 w 평면(좌표(u, v))으로 변환하는 것으로 간주하는 경우가 많습니다.

복소 평면 표기법

복소평면은 C $\mathbb {C}$ \ $displaystyle \mathbb {C$ 로 $\mathbb {C}$ 됩니다 $.$

아르간드 도표

복소 평면에서 복소수 점 z = x + yi의 기하학적 표현입니다.원점에서 점 z = x + yi까지의 선을 따른 거리는 z의 계수 또는 절대값입니다.각도 θ는 z의 인수이다.

아르간드 다이어그램은 x축을 실축으로, y축을 ^[3]허축으로 사용하여 복소수의 기하학적 그림을 $점$ z $= x$ + $iy$ 로 나타냅니다.이러한 플롯은 노르웨이-덴마크 육상 측량가이자 수학자인 카스파르 베셀 (1745–1818)^{[note 3]}에 의해 처음 설명되었지만, 장-로버트 아르간 (1768–1822)의 이름을 따서 명명되었다.아르간드 다이어그램은 복합 평면에서 함수의 0과 극의 위치를 플롯하는 데 자주 사용됩니다.

입체 투영

복소평면의 한 점을 제외한 구상의 모든 점을 매핑하는 리만 구

복잡한 평면이 구면을 차지하고 있는 것처럼 생각하면 유용할 수 있습니다.단위 반지름의 구가 주어진 경우 구상의 적도가 평면 내의 단위 원과 일치하고 북극이 평면 "위"에 오도록 복소 평면의 원점에 중심을 배치합니다.

북극을 뺀 구면상의 점과 복소평면상의 점과의 일대일 대응관계를 다음과 같이 설정할 수 있다.평면에 점을 지정하면 해당 점을 구의 북극과 연결하는 직선을 그립니다.그 선은 정확히 하나의 다른 점에서 구의 표면을 교차할 것이다. $z$ = $0$ 지점은 구의 남극에 투영된다.단위 원의 내부가 구 안에 있으므로 전체 영역( $z$ < 1)이 남반구에 매핑됩니다.단위 원 자체( $z$ = $1$ )는 적도에 매핑되고 단위 원 $외부 (z$ > 1)는 북극을 뺀 북반구에 매핑됩니다.분명히 이 절차는 가역적입니다.북극이 아닌 구면상의 어떤 점에서도 그 점을 북극에 연결하고 정확히 한 점에서 평면과 교차하는 직선을 그릴 수 있습니다.

이 입체 투영에서 북극 자체는 복합 평면의 어떤 점과도 연관되지 않는다.우리는 복잡한 평면에 1개의 점(일명 무한대의 점)을 더하고 구상의 북극과 식별함으로써 일대일 대응 관계를 완성한다.이 토폴로지 공간(복소 평면 + 무한대 점)을 확장 복소 평면이라고 합니다.우리는 복잡한 분석을 논의할 때 단일 "무한점"을 언급합니다.실수선에는 무한대(양수 및 음수)에 두 개의 점이 있지만 확장 복합 ^[5]평면에는 무한대(북극)에 한 점만 있습니다.

위도와 경도의 선이 구면에서 평면 위로 투영될 때 어떤 일이 일어날지 잠시 상상해 보십시오.위도 선은 모두 적도에 평행하므로 $원점$ z = $0$ 을 중심으로 완벽한 원이 됩니다. 그리고 경도 선은 원점을 통과하는 직선이 됩니다(구상의 북극과 남극을 모두 통과하기 때문에 "무한점"도 통과합니다).

이것은 두 개 이상의 값으로 구성된 평면에 구체를 투영하는 유일한 가능하지만 그럴듯한 입체 상황은 아니다.예를 들어, 구의 북극은 원점에 접하는 평면에서 $원점$ z = $-1$ 의 맨 위에 배치될 수 있습니다.디테일은 별로 중요하지 않아요.평면에 구체를 입체적으로 투영하면 "무한점에 있는 점"이 하나 생성되며, 구체의 위도와 경도의 선을 평면에 각각 원과 직선으로 매핑합니다.

평면 절단

복합 변수의 함수를 논할 때 종종 복합 평면의 절단을 생각하면 편리합니다.이 생각은 몇 가지 다른 맥락에서 자연스럽게 발생한다.

다중값 관계 및 분기점

단순한 두 값 관계를 고려합니다.

w=f(z)=\pm {nfrt {z}=z^{1/2}.

이 관계를 단일값 함수로 취급하기 전에 결과값의 범위를 제한해야 합니다.음수가 아닌 실수의 제곱근을 다룰 때 이것은 쉽게 할 수 있다.예를 들어, 우리는 단지 그 정의만 내릴 수 있다.

y=g(x)=syslogrt {x}=x^{1/2}

y = $x$ 가 $되도록 2$ 음이 아닌 실수 y가 되어야 한다.이 아이디어는 2차원 복잡한 평면에서는 잘 작동하지 않는다.그 이유를 알아보려면 점 z가 단위 원을 따라 이동함에 따라 f(z) 값이 어떻게 변하는지 생각해 보겠습니다.우리는 쓸 수 있다

\displaystyle z=re^{i\theta}\take w=z^{1/2}=sqrt {r},e^{i\theta /2}\qquad(0\leq \theta \leq 2\pi)}

분명히 z는 원을 따라 이동하기 때문에 원의 절반만 추적합니다.따라서 복소 평면에서 연속되는 하나의 운동은 양의 제곱근⁰ e = 1을 음의 $제곱근 iπ$ e = $-1$ 로 변환했다.

이 문제는 점 z = 0의 제곱근은 1개이고 다른 복소수 z 0 0은 정확히 2개의 제곱근을 가지기 때문에 발생합니다.실수선에서는 단일 점 x = 0에 "변형"을 세워 이 문제를 회피할 수 있었다. 복잡한 평면에 닫힌 윤곽이 분기점 z = 0을 완전히 둘러싸지 않도록 하려면 더 큰 장벽이 필요하다.이는 일반적으로 분기 절단을 도입함으로써 이루어진다. 이 경우 "절단"은 z = 0 지점에서 양의 실제 축을 따라 무한대 지점까지 확장될 수 있으므로 절단 평면에서 변수 z의 인수는 0 µ arg(z) < 2µ 범위로 제한된다.

우리는 지금)z.mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{w에 관한 완벽한 설명을 줄 수 있다.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1⁄2.그러기 위해서는 각각 실제 축을 따라 잘라낸 z-plane 복사본이 두 개 필요합니다.한 복사본에서는 1의 제곱근을 e = $1$ 로 $정의$ 하고⁰ 다른 복사본에서는 1의 제곱근을 e = -1로 정의합니다^iπ.우리는 이 두 개의 완전한 절단 평면 시트를 복사라고 부릅니다.연속성 인수를 지정하면 (현재 단일값) $함수$ w = $z$ 가^1⁄2 첫 번째 시트를 w-plane의 상반부에 매핑하고, 두 번째 시트를 w-plane의 하반부에 매핑하는 것을 알 수 있습니다( $여기$ 서 $π$ ( arg( $w)$ < $2$ ^[6]≤ ） ( ( arg(w) < 2 ≤ )

이 예에서 분기 절단은 실제 축을 따라 배치될 필요가 없습니다.일직선이 될 필요도 없어요.원점 z = 0과 무한대의 점을 연결하는 모든 연속 곡선이 작동합니다.경우에 따라서는 분기 절단이 무한대의 지점을 통과할 필요도 없습니다.예를 들어, 관계를 생각해 봅시다.

{{displaystyle w=g(z)=\left(z^{2}-1\right)^{1/2}.}

여기서 다항식² z - 1은 z = ± $1일$ $때$ 사라지므로 g는 분명히 두 개의 분기점을 갖는다.우리는 실제 축을 따라 평면을 -1에서 1로 "절단"하여 g(z)가 단일값 함수인 시트를 얻을 수 있다.또는 z = 1에서 무한대의 지점을 통해 양의 실제 축을 따라 이동한 다음, 음의 실제 축을 다른 분기 지점인 z = -1로 "상향"시킬 수 있습니다.

이 상황은 위에서 설명한 입체 투영을 사용하여 가장 쉽게 시각화할 수 있습니다.구면에서 이러한 절단 중 하나는 남반구를 종방향으로 관통하여 적도의 점(z = -1)을 적도(z = 1)의 다른 점(원점, z = 0)과 연결하고 도중에 남극(원점, z = 0)을 통과한다.두 번째 절단은 북반구를 종방향으로 관통하고 북극(즉 무한대의 점)을 통과함으로써 동일한 두 적도 지점을 연결합니다.

meromaphile 함수의 영역 제한

meromape 함수는 유한하거나 셀 수 있을 정도로 ^{[note 4]}무한하지 않은 점을 제외하고 영역의 모든 곳에서 해석되는 복잡한 함수입니다.이러한 함수를 정의할 수 없는 점을 다중 함수의 극이라고 합니다.때때로 이 모든 기둥들은 일직선으로 놓여 있다.이 경우 수학자들은 함수가 "절단면 위의 정형"이라고 말할 수 있다.여기 간단한 예가 있습니다.

감마 함수는 다음과 같이 정의된다.

\Gamma (z) = snfrac {e^{-\frac z} {z}} \ right [ \ left [ \ left ( 1 + { \ frac {z } { n} \ right ]^{ - 1 } e ^{ z / n } \ right } }

여기서 θ는 오일러-마셰로니 상수이며, z가 0일 때, 즉 ^{[note 5]}음의 정수일 때 무한곱에서 정확히 하나의 분모가 사라지기 때문에 0, -1, -2, -3, ...에 단순 극을 가진다.모든 극이 음의 실제 축에 위치하기 때문에, z = 0에서 무한대의 점까지 이 함수는 "절단면에서 음의 실제 축을 따라 뻗어나가는 절단 부분, 0(표준)에서 무한대의 점까지"로 설명할 수 있다.

또는 δ(z)는 "-solat < arg(z) < θ이고 z = 0을 제외한 절단면 내 holomiform"으로 설명할 수 있다.

이 절단은 이전에 접한 분기 절단과 약간 다릅니다. 절단면에서 음의 실제 축을 제외하기 때문입니다.분기절단은 절단면에 연결된 실제 축을 한쪽에 남겨두고(0 ≤ ), ), ), ）, 반대쪽을 따라 절단면에서 절단하였다( < < 2 π ）。

물론 δ(z)가 정형인 도메인을 구성하기 위해 전체 선분을 z = 0에서 -segment까지 제외할 필요는 없다.우리가 정말로 해야 할 일은 {0, -1, -2, -3, ...}의 셀 수 없을 정도로 무한한 점 집합에서 평면을 천공하는 것이다. 그러나 천공된 평면의 닫힌 윤곽선은 δ(z)의 극 중 하나 이상을 둘러싸서 잔차 정리에 의해 반드시 0이 될 필요는 없는 윤곽 적분을 제공할 수 있다.복잡한 평면을 절단함으로써 우리는 δ(z)가 이 제한된 영역에서 완전 형상임을 보장할 뿐만 아니라 절단면에 있는 모든 닫힌 곡선에 걸친 δ의 등고선 적분이 0과 동일하게 되도록 보장한다.

컨버전스 지역 지정

많은 복잡한 함수는 무한 급수 또는 연속 분수로 정의됩니다.이러한 무한히 긴 식을 분석할 때 기본적으로 고려해야 할 사항은 이들이 유한값으로 수렴하는 복소 평면의 부분을 식별하는 것이다.다음 예시와 같이 평면을 절단하면 이 프로세스가 쉬워질 수 있습니다.

무한 급수에 의해 정의된 함수를 고려합니다.

{{displaystyle f(z)=\sum _{n=1}^{\infty}\left(z^{2}+n\right)^{-2}.}

모든 복소수 z에 대해 z =(-z)²이므로² f(z)가 z의 짝수 함수이므로 분석을 복소 평면의 절반으로 제한할 수 있습니다.그리고 시리즈가 정의되지 않았기 때문에

z^{2}+n=0\displays \iff \displays z=\pm isqrt {n}

z가 순수한 ^{[note 6]}허수일 때 f(z)를 조사하는 더 힘든 작업을 수행하기 전에 전체 허수 축을 따라 평면을 자르고 z의 실제 부분이 0이 아닌 이 시리즈의 수렴을 설정하는 것이 이치에 맞는다.

이 예에서는 무한합이 정의되지 않은 점이 격리되어 있고 절단면을 적절한 펑크 평면으로 대체할 수 있기 때문에 절단은 단순한 편리함입니다.상황에 따라서는 편리한 것뿐만 아니라 절단이 필요한 경우도 있습니다.무한 주기 연속 분율을 고려합니다.

f(z)=1+{\displayac {z}{1+{\displayac {z}{1+{\displayac {z}}}}}}}.

z가 z < -1 $-4$ 와 $같은$ 음의 $실수$ 가 아닌 경우에만 f(z)가 유한값으로 수렴한다는 것을 알 수 있다.즉, 이 연속된 분수에 대한 수렴 영역은 컷 평면으로, 컷이 음의 실제 축을 따라 -1⁄4에서 ^[8]무한대의 점까지 진행됩니다.

절단 평면을 다시 접착

우리는 이미 그 관계가 어떻게 되어가는지 보았다.

{\displaystyle w=f(z)=\pm({displayrt {z}}=z^{1/2}})

f 영역을 두 개의 분리된 시트로 분할하여 단일 값 함수로 만들 수 있습니다. $f$ $(z$ )= $z$ 가^1/2 $전체$ w 평면인 홀모픽 함수로 정의될 수 있는 $단일$ 리만 표면을 형성하기 위해 두 시트를 다시 "결합"할 수도 있다(점 w = $0$ 제외).작동 방식은 이렇습니다.

z = $0$ 에서 무한대의 점까지 양의 실제 축을 따라 연장되는 절단 복합 평면의 복사본 두 개를 상상해 보십시오.한 장에 0 $µ$ arg( $z)$ < $2µ$ 를 $정의$ 하여^1/2 $정의상 0$ 1 = $e$ = 1로 한다.두 번째 시트에는 정의상 $1 =$ e $= -1이 되도록 1/2$ $2µ$ $arg iπ$ ( $z)$ < 4µ를 정의한다.이제 거꾸로, 그래서 가상의 축 둘 다 진정한 축이 같은 방향으로 가리키는은 첫번째 시트,는 두장"접착제"(그 첫번째 시트의 가장자리를 붙인"θ)0"에 반대 방향으로도 허축점 가장자리로 두번째 시트 위에"θ<>4π"표시 연결되어 있고, 두번째 시트 flip. 교육 $두$ 번째 시트의 ge는 첫 번째 시트의 ge < $2bc$ '라는 레이블이 붙은 가장자리에 연결됩니다.결과는 f $(z)$ = $z$ 가^1/2 $단일$ 값이고 완전 형상인 $리만$ 표면 $영역$ 이다(z = ^[6]0인 경우 제외).

f가 이 영역에서 단일 값인 이유를 이해하려면 첫 번째 시트의 z = $1$ 부터 $시작$ 하는 단위 원 주위의 회로를 상상해 보십시오. $0$ ≤ $π$ < 2 $we$ 、 아직 첫 번째 시트 위에 있습니다. $θ$ = $2$ we이면 두 번째 시트로 넘어갔으며, 두 개의 시트를 접착하는 방식 때문에 시작점으로 돌아가기 전에 $분기점$ z = $0$ 주위에 두 번째 완전한 회로를 만들어야 합니다. 여기서 $θ$ = $4$ is = $0$ 에 해당합니다.즉, 변수 z가 분기점을 중심으로 두 바퀴를 완전히 돌 때 w면 내의 z 화상은 하나의 완전한 원만 추적합니다.

형식적인 차별화를 통해 알 수 있습니다.

f(z)=z^{1/2}\crightarrow\crack f'(z)=crighttfrac {1}{2}}z^{-1/2}

여기서 f의 도함수는 z = $0일$ $때$ (즉, z = $0일$ $때$ 제외)를 제외하고 리만 표면 어디에나 존재하고 유한하다는 결론을 내릴 수 있다.

함수에 대한 리만 표면은 어떻게 할 수 있는가?

{{displaystyle w=g(z)=\left(z^{2}-1\right)^{1/2}}

또한 위에서 논의한 바와 같이, 구축되어야 하는가?다시 두 개의 z-평면 복사본으로 시작하지만, $이번$ 에는 z = $-1$ 에서 z = 1까지 이어지는 실제 선분을 따라 각 복사본이 잘려나갑니다. 이것이 g(z)의 두 분기점입니다.이 중 하나를 거꾸로 뒤집으면 두 개의 가상 축이 반대 방향을 가리키고 두 컷 시트의 해당 모서리를 접착합니다.z = $1$ 을 $중심$ 으로 한 단위 반지름 원의 원을 중심으로 회로를 추적하여 g가 이 표면에서 단일 값 함수임을 확인할 수 있습니다. 첫 번째 $시트$ 의 $z$ = 2 지점에서 시작하여 $z$ = $0$ 에서 절단을 만나기 전에 원의 반 바퀴를 돌립니다.절단은 z가 분기점 z = $1$ 을 중심으로 한 바퀴를 완전히 추적했을 때 w가 전체 $회전$ 의 절반만 걸렸을 때 w의 기호는 반전되었고(e = $-1$ $이후 iπ$ ), 우리의 경로는 표면의 두 번째 시트의 z = $2$ 지점으로 $우리$ 를 이동시켰다.또 다른 반바퀴를 돌면 절단면의 반대편( $z$ = $0$ )을 만나 분기점을 두 바퀴 완전히 돌면 마침내 시작점(첫 번째 시트의 z = $2$ )에 도달합니다.

$이$ 예에서 $= arg$ ( $z)$ 에 라벨을 붙이는 자연스러운 방법은 첫 번째 시트에 $-setting$ < $>$ 를 $설정$ 하고 두 번째 시트에 $"<$ > $3$ "을 설정하는 것입니다.두 시트의 가상 축은 반대 방향을 가리키므로 닫힌 윤곽선이 한 시트에서 다른 시트로 이동할 때 시계 반대 방향의 양의 회전 감각이 유지됩니다(두 번째 시트는 거꾸로 되어 있음).이 표면이 xy 평면에 평행한 두 시트가 있는 3차원 공간에 포함되어 있다고 상상해 보십시오.그리고 표면에 수직 구멍이 있는 것처럼 보이는데, 여기서 두 개의 절단 부분이 함께 결합됩니다.절단이 실제 $축$ 을 $따라$ z = -1에서 무한대 지점까지, $z$ = 1에서 $실제$ 축을 따라 절단이 이루어지면 어떻게 됩니까?다시 리만 표면을 구성할 수 있지만, 이번에는 "구멍"이 수평입니다.위상학적으로 볼 때, 이 리만 표면의 두 버전은 동일하며, 이들은 1속 방향성이 있는 2차원 표면입니다.

제어 이론에서 사용

제어 이론에서는 복합 평면을 s 평면이라고 합니다.시스템의 동작(특성 방정식)을 그래픽으로 설명하는 방정식의 뿌리를 시각화하는 데 사용됩니다.이 방정식은 보통 라플라스 변환의 매개변수 's'에서 다항식으로 표현되므로 's' 평면이라는 이름이 붙습니다.s-평면의 포인트는 s $=$ + j ${\$ { $displaystyle$ s $=\displays$ + $j\obe$ 의 형태를 취하며, 여기서 'j'는 가상의 구성요소를 나타내기 위해 일반적인 'i' 대신 사용됩니다.

복합 평면의 또 다른 관련 용도는 나이키스트 안정성 기준이다.이는 복합 평면에서 주파수(또는 루프 전송 함수)의 함수로서 개방 루프 크기와 위상 응답의 나이키스트 플롯을 검사하여 폐쇄 루프 피드백 시스템의 안정성을 결정할 수 있는 기하학적 원리입니다.

z 평면은 s 평면의 이산 시간 버전이며, 여기서 Laplace 변환 대신 z 변환이 사용됩니다.

이차 공간

복소 평면은 두 개의 서로 다른 2차 공간과 연관되어 있습니다.복소 평면에서의 $점$ z $= x$ + $iy$ 에 대해, 제곱 함수² z와 노름 $x^{2}+y^{2}$ x $x^{2}+y^{2}$ + $x^{2}+y^{2}$ 2(\ $displaystyle$ x $^{2}+y^{2})$ 는 $x^2 + y^2$ 모두 2차 형식이다.전자는 복합 평면에서 미터법을 사용한 후 종종 무시된다.2차 공간으로서의 복소 평면의 이러한 구별되는 면은 케일리-딕슨 과정을 통해 장에 걸친 대수학 구조에서 발생한다.이 절차는 어느 필드에나 적용할 수 있으며, 필드 R과 C에 대해 다른 결과가 발생합니다.R이 이륙 필드일 경우 C는 $x^{2}+y^{2},$ $x^{2}+y^{2},$ x 2 + $x^{2}+y^{2},$ 2, $x^{2}+y^{2},$ {\ $display$ x $^{2}+y^{2$ }로 $x^{2}+y^{2},$ 구성되지만, 프로세스는 C와² z로 시작할 수 있으며, 이 경우 R에서 파생된 것과 다른 대수가 생성됩니다.어떤 경우에도 생성된 대수는 합성 대수로, 이 경우 복소평면은 두 개의 다른 합성 대수에 대해 설정된 포인트이다.

"복잡한 평면"의 다른 의미

이 기사의 이전 섹션에서는 복소수의 기하학적 표현 측면에서 복소 평면을 다룬다."복소 평면"이라는 용어의 사용은 오래되고 수학적으로 풍부한 역사를 가지고 있지만, "복소 평면"으로 특징지을 수 있는 유일한 수학적 개념은 결코 아니다.적어도 세 가지 추가 가능성이 있습니다.

2차원 복소 벡터 공간, 즉 좌표가 복소수인 2차원 벡터 공간이라는 의미에서의 "복소 평면"입니다.다음 항목도 참조하십시오.복잡한 아핀 공간 two 2차원.
(1 + 1)차원 민코프스키 공간은 분할 복소 평면이라고도 하며 대수 분할 복소수가 데카르트 평면의 점 $(x,$ $y)$ 과 쉽게 연관되는 두 개의 실제 성분으로 분리될 수 있다는 점에서 "복소 평면"이다.
실수에 걸친 이중 숫자 집합은 데카르트 평면의 점 $(x,$ $y)$ 과 일대일로 대응시킬 수 있으며 "복소 평면"의 또 다른 예를 나타냅니다.

「」를 참조해 주세요.

만델브로트 프랙탈, 복잡한 평면에 이미징된

메모들

^ 완전한 아크탄젠트의 관점에서 복잡한 인수의 상세한 정의는 atan2 함수의 설명에서 찾을 수 있다.
^ 복소수 지수 함수, 삼각 함수 및 복소수 로그의 모든 $e^{z}$ 한 속성은 $e^{z}$ e $z$ 의 멱급수열에서 직접 추론할 수 있습니다. 특히 $\log r$ r \ $displaystyle \log$ $e^{z}$ $r$ $e^{z}$ $|r|=1$ \ $displaystyle$ r $1$ ) 。기하학적 ^[1]또는 삼각구조를 참조하지 않고 레이트를 적용했습니다.
^ 베셀의 회고록은 1797년에 덴마크 아카데미에 제출되었고, 아르간드의 논문은 1806년에 ^[4]출판되었다.
^ 홀모픽 함수가 해석적이라는 증명도 참조하십시오.
^ δ(z)에 대한 무한곱은 분모가 사라지지 않는 경계 영역에서 균일하게 수렴하므로 복소 평면에서 ^[7]meromape 함수를 정의합니다.
^ Re(z) > 0일 때, 이 합은 θ(2)와 비교하여 모든 경계 영역에서 균일하게 수렴한다. 여기서 θ(s)는 리만 제타 함수이다.

레퍼런스

^ (Whittaker & Watson 1927), 부록을 참조하십시오.
^ (Whittaker & Watson 1927), 페이지 10을 참조하십시오.
^ Weisstein, Eric W. "Argand Diagram". mathworld.wolfram.com. Retrieved 19 April 2018.
^ (Whittaker & Watson 1927), 페이지 9를 참조하십시오.
^ (Flanigan 1983), 페이지 305를 참조하십시오.
^ ^a ^b (Moretti 1964), 페이지 113–119를 참조하십시오.
^ (Whittaker & Watson 1927), 페이지 235 – 236을 참조하십시오.
^ (1948년 벽), 페이지 39를 참조하십시오.

인용된 저작물

Flanigan, Francis J. (1983). Complex Variables: Harmonic and Analytic Functions. Dover. ISBN 0-486-61388-7.
Moretti, Gino (1964). Functions of a Complex Variable. Prentice-Hall.
Wall, H. S. (1948). Analytic Theory of Continued Fractions. D. Van Nostrand Company. 첼시 출판사 ISBN 0-8284-0207-8에 의해 전재(1973).
Whittaker, E. T.; Watson, G. N. (1927). A Course in Modern Analysis (Fourth ed.). Cambridge University Press.

외부 링크

Weisstein, Eric W. "Argand Diagram". MathWorld.
Jean-Robert Argand, "Essai sur un maniére de représenter des quantités imaginaires déométriques", 1806년 온라인 및 BibNum에서 분석(영어판은 'a télecharger' 클릭)

[1] 완전한 아크탄젠트의 관점에서 복잡한 인수의 상세한 정의는 atan2 함수의 설명에서 찾을 수 있다.

[3] 복소수 지수 함수, 삼각 함수 및 복소수 로그의 모든 $e^{z}$ 한 속성은 $e^{z}$ e $z$ 의 멱급수열에서 직접 추론할 수 있습니다. 특히 $\log r$ r \ $displaystyle \log$ $e^{z}$ $r$ $e^{z}$ $|r|=1$ \ $displaystyle$ r $1$ ) 。기하학적 ^[1]또는 삼각구조를 참조하지 않고 레이트를 적용했습니다.

[7] 베셀의 회고록은 1797년에 덴마크 아카데미에 제출되었고, 아르간드의 논문은 1806년에 ^[4]출판되었다.

[10] 홀모픽 함수가 해석적이라는 증명도 참조하십시오.

[12] δ(z)에 대한 무한곱은 분모가 사라지지 않는 경계 영역에서 균일하게 수렴하므로 복소 평면에서 ^[7]meromape 함수를 정의합니다.

[13] Re(z) > 0일 때, 이 합은 θ(2)와 비교하여 모든 경계 영역에서 균일하게 수렴한다. 여기서 θ(s)는 리만 제타 함수이다.

[2] (Whittaker & Watson 1927), 부록을 참조하십시오.

[4] (Whittaker & Watson 1927), 페이지 10을 참조하십시오.

[5] Weisstein, Eric W. "Argand Diagram". mathworld.wolfram.com. Retrieved 19 April 2018.

[6] (Whittaker & Watson 1927), 페이지 9를 참조하십시오.

[8] (Flanigan 1983), 페이지 305를 참조하십시오.

[Moretti-9] (Moretti 1964), 페이지 113–119를 참조하십시오.

[11] (Whittaker & Watson 1927), 페이지 235 – 236을 참조하십시오.

[14] (1948년 벽), 페이지 39를 참조하십시오.

[note 1]

[note 2]

[2]

[3]

[note 3]

[5]

[6]

[note 4]

[note 5]

[note 6]

[8]

[1]

[4]

[7]

Search

복소 평면

네임스페이스

더

목차

표기법