단열 과정

열역학
고전적인 카르노 히트 엔진
나뭇가지 고전적인 통계 화학의 양자 열역학 평형/비평형
법률 제로스 첫번째 둘째 셋째
시스템들 폐쇄형 시스템 오픈 시스템 격리 시스템 주 상태 방정식 이상 기체 실가스 상황 위상(매터) 평형 볼륨 제어 인스트루먼트 과정 이소바릭 아이소코리 등온 단열성 등엔트로픽 이센탈픽 준정전성 폴리트로픽 자유 확장 가역성 불가역성 내복원성 사이클 히트 엔진 히트 펌프 열효율
시스템 속성 주의: 이탤릭체로 표시된 켤레 변수 속성도 집약적이고 광범위한 속성 프로세스 기능 일하다. 열 국가 기능 온도/엔트로피(개요) 압력/볼륨 화학 퍼텐셜/입자수 증기 품질 속성 감소
재료 특성 속성 데이터베이스 비열 용량 ${\displaystyle c=}$ ${\displaystyle T}$ $\displaystyle \partial S\$ ${\displaystyle N}$ ${\displaystyle\partial T}$ 압축성 $\displaystyle \displays =-}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ $(\displaystyle\displayp)$ 열팽창 $\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ ${\displaystyle\partial T}$
방정식 카르노의 정리 클라우시우스 정리 기본 관계 이상기체의 법칙 맥스웰 관계 온사저 호혜 관계 브리지만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 ${\displaystyle A(T,V)=U-TS}$ 깁스 자유 에너지 ${\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스 법칙 "영구 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너제틱스 이론들 열량론 Vis viva ('생체력') 열의 기계적 등가 동력 주요 출판물 실험적인 질문 ~에 대해서열 균형에 대하여 이종 물질 의 리플렉션 불의 원동력 타임라인 열역학 히트 엔진 예체능 교육 맥스웰의 열역학 표면 에너지 분산으로서의 엔트로피
과학자 베르누이 볼츠만 브리지만 카라테오도리 카르노 클라피론 클라우시우스 돈더 듀헴 깁스 폰 헬름홀츠 줄 루이스 마시외 맥스웰 폰 메이어 네른스트 온사게 플랑크 랭킨 스미톤 스틸 태트 톰슨 톰슨 판 데르 발스 워터스톤
다른. 핵생성 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

열역학에서, 단열 과정(그리스어: adiabatos, "통과 불가능한")은 열역학 시스템과 그 환경 사이에 열이나 질량을 전달하지 않고 발생하는 열역학 과정의 한 종류이다.등온 과정과는 달리, 단열 과정은 단지 ^[1][2]일로서 에너지를 주변으로 전달합니다.열역학에서 중요한 개념으로서, 단열 과정은 열역학 제1법칙을 설명하는 이론을 뒷받침합니다.

일부 화학 및 물리적 과정은 에너지가 열로 시스템에 들어오거나 나가는 속도가 너무 빠르기 때문에 편리한 "단열 근사"^[3]가 가능합니다.예를 들어, 단열 화염 온도는 이 근사치를 사용하여 연소가 주위에 열을 잃지 않는다고 가정하여 화염 온도 상한을 계산합니다.

기상학 및 해양학에서 단열 냉각은 습기 또는 염도의 응축을 일으켜 소포를 과도하게 포화시킵니다.따라서 초과분을 제거해야 합니다.이 과정에서 응축된 액체 물이나 염분이 이상화된 순간 강수에 의해 제거되는 것으로 가정하는 의사 단열 과정이 된다.압축된 구획이 따뜻해지고 ^[4]포화 상태가 낮은 상태로 유지되기 때문에 의사 방사선 프로세스는 팽창만을 위해 정의됩니다.

묘사

Q = 0이 되도록 시스템에 열이 전달되거나 전달되지 않는 과정을 단열이라고 하며, 이러한 시스템을 단열적으로 ^[5][6]분리한다고 합니다.공정이 단열이라는 가정은 자주 제기되는 단순화 가정입니다.예를 들어, 엔진의 실린더 내에서 가스의 압축은 매우 빠르게 발생하는 것으로 가정되며 압축 프로세스의 시간 척도에 따르면 시스템의 에너지의 거의 열로 주변으로 전달되지 않습니다.실린더는 절연되지 않고 전도성이 매우 높지만, 이 프로세스는 단열로 이상적입니다.이러한 시스템의 확장 프로세스도 마찬가지라고 말할 수 있다.

단열 격리의 가정은 유용하며 종종 시스템 동작의 좋은 첫 번째 근사치를 계산하기 위해 그러한 다른 이상화와 결합된다.예를 들어, 라플레이스에 따르면, 소리가 기체 내에서 이동할 때, 매체 내에서 열전도를 위한 시간이 없기 때문에, 소리의 전파는 단열적입니다.E)γP, 비열의 일정한 압력에 γ 비율과 일정한 부피에서의(γ).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{ 그러한 단열 절차를 위해, 탄력성(영률)의 탄성 계수이고 표현될 수 있다.디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}Cp/Cv)고 가스의 P는 압력이다.

단열 가정의 다양한 적용

닫힌 시스템의 경우 열역학 제1법칙은 δU = Q - W로 표기할 수 있습니다. 여기서 δU는 시스템의 내부 에너지의 변화, Q는 열에 의해 추가된 에너지의 양, 그리고 W는 시스템이 주위에 가해지는 작업을 나타냅니다.

• 시스템이 내부 또는 외부로 이동할 수 없는 견고한 벽(W = 0)을 가지고 있고 벽이 단열 상태가 아니며 에너지가 열의 형태로 추가되며(Q > 0), 위상 변화가 없으면 시스템의 온도가 상승합니다.
• 시스템에 압력-부피 작업이 수행될 수 없는 강체 벽이 있지만 벽은 단열(Q = 0)이며, 시스템 내에서 마찰 또는 점성 유체의 교반(W < 0)의 형태로 에너지가 추가되며, 위상 변화가 없으면 시스템의 온도가 상승합니다.
• 시스템 벽이 단열형(Q = 0)이지만 강성이 없는(W ≤ 0) 경우, 가공의 이상화 프로세스에서 에너지가 무마찰, 비마찰 압력-부피 작업(W < 0)의 형태로 시스템에 추가되고 위상 변화가 없으면 시스템의 온도가 상승합니다.이러한 과정은 등엔트로픽 과정이라고 불리며 "가역적"이라고 한다.이상적으로는 프로세스가 역전되면 에너지가 시스템에 의해 수행된 작업처럼 완전히 회수될 수 있습니다.시스템에 압축 가능한 가스가 포함되어 있고 부피가 감소하면 가스 위치의 불확실성이 감소하여 시스템의 엔트로피를 감소시키지만 프로세스가 등방적이므로 시스템의 온도가 상승합니다(δS = 0).마찰력 또는 비스코스력이 시스템 내에서 작용하도록 작업이 추가되면 프로세스는 등방성이 아니며 상변화가 없으면 시스템의 온도가 상승하고 프로세스가 "불가역적"이라고 하며 시스템에 추가된 작업이 작업 형태로 완전히 복구되는 것은 아닙니다.
• 시스템의 벽이 단열하지 않고 에너지가 열로 전달되면 엔트로피가 열과 함께 시스템에 전달된다.이러한 과정은 단열도 등엔트로픽도 아니며 열역학 제2법칙에 따라 Q > 0과 δS > 0을 가진다.

자연적으로 발생하는 단열 과정은 되돌릴 수 없다(엔트로피가 생성된다).

단열적으로 분리된 시스템으로의 작업으로서의 에너지 전달은 두 가지 이상화된 극단적 종류로 상상할 수 있습니다.이러한 종류의 경우 시스템 내에서 엔트로피가 생성되지 않으며(마찰, 점성 소산 등), 작업은 압력-볼륨 작업(PdV로 표시)일 뿐이다.자연에서, 이 이상적인 종류는 무한히 느린 프로세스를 필요로 하고 낭비의 원인이 없기 때문에 대략적으로만 발생합니다.

또 다른 극단적인 종류의 작업은 등화성 작업(dV = 0)으로, 시스템 내에서 마찰이나 점성 소산을 통해서만 에너지가 작업으로 추가됩니다.단열적으로 격리된 시스템의 점성 유체에 에너지를 전달하는 교반기는 위상 변화 없이 유체의 온도 상승을 일으키지만, 그 작업은 복구할 수 없습니다.등각 작업은 되돌릴 ^[7]수 없습니다.열역학 제2법칙은 에너지 전달의 자연적 과정은 항상 적어도 등화학적 일, 그리고 종종 이 두 가지 극단적인 일 모두로 이루어진다는 것을 관찰한다.마찰이나 점도는 항상 어느 정도 존재하기 때문에 단열이든 아니든 모든 자연 과정은 δS > 0으로 되돌릴 수 없다.

단열 난방 및 냉방

가스의 단열 압축은 가스의 온도 상승을 일으킨다.압력에 대한 단열 팽창 또는 스프링은 온도 저하를 일으킵니다.반대로 자유팽창은 이상적인 기체를 위한 등온 과정이다.

단열 가열은 예를 들어 피스톤이 실린더 내에 포함된 가스를 압축하고 많은 실제 상황에서 벽을 통한 열전도가 압축 시간에 비해 느려질 수 있는 온도를 상승시킴으로써 가스에 가해지는 압력에 의해 가스의 압력이 상승할 때 발생합니다.이는 압축 행정 중 열 방산 부족에 의존하여 연료 증기 온도를 충분히 상승시켜 점화시키는 디젤 엔진에 실용적으로 적용될 수 있습니다.

단열 가열은 기단이 하강할 때, 예를 들어 카타바틱 바람, hn풍, 산맥을 타고 내려오는 치누크 바람과 같이 지구의 대기에서 발생합니다.공기 소포가 내려오면, 소포에 가해지는 압력이 증가합니다.이러한 압력의 상승으로 인해 공기 구획에 대한 작업이 수행됨에 따라 소포의 부피가 감소하고 온도가 상승하여 내부 에너지가 증가하며, 이는 공기 덩어리의 온도 상승으로 나타납니다.공기의 구획은 전도 또는 방사선(열)에 의해서만 에너지를 천천히 소멸시킬 수 있으며, 첫 번째 근사치까지 단열적으로 격리된 것으로 간주되며 프로세스는 단열 프로세스로 간주될 수 있습니다.

단열 냉각은 단열적으로 격리된 시스템의 압력이 감소하여 팽창할 수 있게 되어 주변 환경에서 작동하게 됩니다.가스 소포에 가해지는 압력이 감소하면 소포 안의 가스가 팽창하게 되고, 부피가 커지면 내부 에너지가 감소하면서 온도가 떨어집니다.단열 냉각은 지구 대기에서 지형적인 상승과 풍파에 의해 발생하며, 이것은 말뚝이나 렌즈 구름을 형성할 수 있다.

산간 지역의 단열 냉각으로 인해 사하라 ^[8]사막의 일부 지역에서는 눈이 자주 내리지 않는다.

단열 냉각에는 유체가 필요하지 않습니다.매우 낮은 온도(절대 0도보다 수천분의 1도 높은 온도)에 도달하는 데 사용되는 기술 중 하나는 단열성 소자이며, 여기서 자성 재료의 자기장 변화는 단열 냉각을 제공하기 위해 사용된다.또 팽창하는 우주의 내용물은 단열 냉각 유체라고 (1차적으로) 설명할 수 있다.(우주의 열사 참조).

솟아오르는 마그마는 분출 전에 단열 냉각을 거치기도 하는데, 킴벌라이트와 ^[9]같이 깊은 곳에서 빠르게 솟아오르는 마그마의 경우 특히 중요합니다.

지구의 암석권 아래의 대류 맨틀(아스테노스피어)에서 맨틀의 온도는 대략 단열(adiabat)입니다.얕은 깊이와 함께 온도가 약간 떨어지는 것은 재료가 지구에 ^[10]있는 얕은 곳의 압력 감소 때문이다.

이러한 온도 변화는 이상적인 가스 법칙 또는 대기 과정의 정수 방정식을 사용하여 정량화할 수 있습니다.

실제로, 어떤 과정도 진정으로 단열적이지 않습니다.많은 프로세스는 대상 프로세스의 시간 척도와 시스템 경계에 걸친 열방산 속도의 큰 차이에 의존하며, 따라서 단열 가정을 사용하여 대략적으로 추정됩니다.완벽한 절연체가 존재하지 않기 때문에 항상 약간의 열 손실이 있습니다.

이상가스(가역공정)

가역적(즉 엔트로피 생성 없음) 단열 과정을 거치는 이상 기체에 대한 수학 방정식은 폴리트로픽 과정^[3] 방정식으로 나타낼 수 있다.

${\displaystyle PV^{\gamma}=\text{text}},$

여기서 P는 압력, V는 부피, 이 경우 n = µ, 여기서

${\displaystyle\displayfrac {C_{P}}{C_{V}}=syslogfrac {f+2}{f}},$

C는_V 일정한 압력에 대한 비열, C는 일정한 체적에 대한 비열, θ는 단열 지수, f는 자유도(단원자 가스의 경우 3, 2원자 가스와 공선 분자의 경우 5, 예를 들어 이산화탄소)이다_P.

단원자 이상 기체의 경우 δ = 5/3이고, 이원자 기체(공기의 주요 성분인 질소 및 산소 등)의 경우 δ = 7/^[11]5이다.위의 공식은 Bose-Einstein 또는 Fermi 가스가 아닌 고전적인 이상 가스(즉, 절대 0도 온도보다 훨씬 높은 가스)에만 적용됩니다.

또한 P와 V 사이의 위의 관계를 다음과 같이 다시 쓰는 데 이상 기체 법칙을 사용할 수 있다.

${\displaystyle P^{1-\gamma}T^{\gamma}=text{displaytext}}$

$(\displaystyle TV^{\gamma-1}=text{text}).}$

여기서 T는 열역학적 온도이다.

단열 압축의 예

가솔린 엔진의 압축 스트로크는 단열 압축의 예로 사용할 수 있습니다.모델은 가정이 실린더의 압축되지 않은 볼륨이 하나의 리터(1L=1000cm^3)0.001m3로);가스 내부는 대기로 질소 분자와 산소만(자유의 5도에 따라서 일종의 이 원자 기체, 그리고 그렇게γ=7/5)로 구성된;엔진의 압축비(그것은10:1은, 압축되지 않은 가스의 1나는 기분이 줄어들고 있기 있o압축되지 않은 가스는 약 실온 및 압력(온도 27°C 또는 300K, 압력 1bar = 100kPa, 즉 전형적인 해수면 대기압)이다.

$디스플레이 스타일P_{1}V_{1}^{\gamma}=\mathrm {pa}_{1}=100,000~{\text{Pa}}\times(0.001~{\text{m}^{3}})^{\frac {7}}}\&=10^{5}\times 6.31\times 10^{-5}\times}{{{{Pa}}}{{{{{{\text}}}}}}}}}}}}}}{{{{{{{{text}}}}}$

따라서 이 예의 단열 상수는 약 6.31Pm입니다^4.2.

이제 가스는 0.1L(0.0001m³) 부피로 압축됩니다. 우리는 열이 벽을 통해 기체에 들어오거나 나가지 않을 정도로 충분히 빠르게 발생한다고 가정합니다.단열 상수는 동일하게 유지되지만 결과적으로 발생하는 압력을 알 수 없습니다.

${\displaystyle P_{2}V_{2}^{\gamma}=\mathrm {pa}_{1}=6.31~{\text{Pa}},{\text{m}}=P\times(0.0001~{\text{m}{3})^{\frac7}{5}{5}$

이제^[12] 최종 압력에 대해 해결할 수 있습니다.

${\displaystyle P_{2}=P_{1}\left({\frac {V_{2}}\right)^{\gamma}=100,000~{\text{Pa}}\times {10}^7/5}=2.51\times 10^{6}~{\text{{{}}}\text{{{{{{Pa}}}}}}}}}}\times$

또는 25.1바.이러한 압력 상승은 단순한 10:1 압축비 이상을 나타냅니다. 이는 가스가 압축될 뿐만 아니라 가스를 압축하기 위해 수행된 작업도 내부 에너지를 증가시키기 때문입니다. 내부 에너지는 가스 온도 상승과 단순 계산 결과보다 높은 압력 상승으로 나타납니다.n은 원래 압력의 10배입니다.

이상적인 가스 법칙인 PV = nRT(n은 몰 단위의 가스량, R은 해당 가스의 가스 상수)를 사용하여 엔진 실린더 내 압축 가스의 온도도 해결할 수 있습니다.초기 조건은 압력 100kPa, 부피 1L, 온도 300K이며 실험 상수(nR)는 다음과 같습니다.

$디스플레이 스타일 {FRAC {\frac}T}}=\mathrm {pa}_{2}=pa}{\text{Pa}}\times 10^{-3}~{\text{m}{3}{300~{\text{K}}}=0.333~{\text{Pa}{\text{m}}{1}}^{{}}}}}}}}}}{{{{{}}}}}}}}}}}}}}}}}}}}.}$

압축 가스는 V = 0.1 L이고 P = 2.51×10⁶ Pa이므로 온도를 해결할 수 있습니다.

${\displaystyle T=time frac {PV}{\mathrm {par}=time frac {2.51\times 10^{6}~{\text {m}^{3}}{.333~{\text {Pa}},{\text m{}}{1}}{k}}{1}}{text}{k}}}}{1}}}}{text}}}}}}{text}}}{text}}}}{text}}}}}}}}}}}}}{$

이는 최종 온도가 753K, 즉 479°C 또는 896°F로 많은 연료의 점화점을 훨씬 상회하는 온도입니다.이러한 이유로 고압 엔진에는 자체 점화되지 않도록 특수 제작된 연료(이러한 온도 및 압력 조건에서 작동할 경우 엔진 노킹이 발생함)가 필요하거나 인터쿨러가 장착된 슈퍼차저가 압력 부스트를 제공하지만 온도 상승이 더 낮은 연료가 유리합니다.디젤 엔진은 매우 높은 가스 온도를 제공하기 위해 일반적으로 압축비가 16:1 이상인 훨씬 더 극단적인 조건에서 작동하므로 분사된 연료가 즉시 점화됩니다.

기체의 단열 자유 팽창

이상기체의 단열자유팽창을 위해 가스를 절연용기 안에 넣은 후 진공상태에서 팽창시킨다.가스가 팽창하는 외부 압력이 없기 때문에 시스템에 의해 또는 시스템에서 수행되는 작업은 0이 됩니다.이 프로세스는 열전달이나 작동을 수반하지 않기 때문에 열역학 제1법칙은 시스템의 순 내부 에너지 변화가 0임을 의미합니다.이상적인 가스의 경우 내부 에너지는 온도에만 의존하기 때문에 온도는 일정하게 유지됩니다.일정한 온도에서 엔트로피는 부피에 비례하기 때문에 이 경우 엔트로피가 증가하므로 이 과정은 되돌릴 수 없습니다.

단열 냉난방 P-V 관계 도출

단열 프로세스의 정의는 시스템에 대한 열 전달이 0, µQ = 0이라는 것입니다.열역학 제1법칙에 따르면

${\displaystyle dU+\delta W=\delta Q=0,}$

(a1)

여기서 dU는 시스템 내부 에너지의 변화이며 µW는 시스템에 의해 실행되는 작업입니다.모든 작업(δW)은 주변으로부터 열 δQ가 공급되지 않으므로 내부 에너지 U를 희생하여 수행해야 합니다.시스템에 의해 수행되는 압력-체적 작업 δW는 다음과 같이 정의된다.

$(\displaystyle \displaystyle W=P,dV).}$

(a2)

단열 과정에서는 P가 일정하게 유지되지 않고 V에 따라 변화한다.

단열 프로세스가 진행됨에 따라 dP와 dV의 값이 서로 어떻게 관련되어 있는지 알아야 합니다.이상 기체(이상 기체 법칙 PV = nRT)의 경우 내부 에너지는 다음과 같이 주어진다.

${\displaystyle U=\alpha nRT=\alpha PV,}$

(a3)

여기서 α는 자유도를 2로 나눈 값이고, R은 보편 가스 상수이고, n은 시스템의 몰 수(상수)입니다.

미분 방정식(a3) 수율

$\displaystyle dU=\alpha nR,dT=\alpha,d(PV)=\alpha(P,dV+V,dP).}$

(a4)

식 (a4)은 C = αR이기 때문에_V 종종 dU = nC_V dT로 표현된다.

이제 방정식 (a2)과 (a4)을 방정식 (a1)로 대입하여 구한다.

${\displaystyle -P,dV=\alpha P,dV+\alpha V,dP,}$

인수분해 -P dV:

$\displaystyle - (\alpha +1)P,dV=\alpha V,dP,}$

양쪽을 PV로 나눕니다.

$(\displaystyle - (\alpha + 1){\frac {dV}{V}}=\alpha {dP}{P}}).}$

V에서₀ V로, P에서 P로 각각 왼쪽과₀ 오른쪽을 통합하고 측면을 바꾼 후,

$(\displaystyle \ln \frac {P}{P_{0}}\right)=-{\frac {\frac +1}{\alpha}}\ln \frac {V}{0}}\right.}$

양쪽을 지수화하고 α + 1/α를 열용량비인 δ로 대체합니다.

${\displaystyle \flac {P} {P_{0}}\right}=\left({\flac {V} {V_{0}}\right})^{-\gamma}}}}$

음의 부호를 제거해서

${\displaystyle \leftfac {P} {P_{0}} \right} = \left({\frac {V_{0}} {V}} \right)^{\gamma } } }$

그러므로,

${\displaystyle \leftfac {P} {P_{0}}\right}\left({\frac {V} {V_{0}}\right)^{\gamma}=1,}$

그리고.

${\displaystyle P_{0}V_{0}^{\gamma}=\mathrm {gamma} .}$

$\displaystyle \Delta U=\alpha RnT_{2}-\alpha RnT_{1}=\alpha Rn\Delta T}$

(b1)

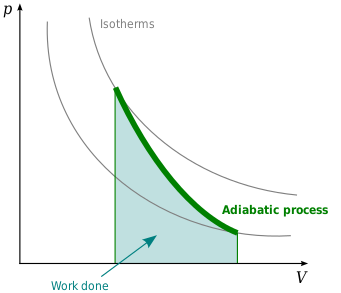
동시에, 압력-부피 변화에 의해 수행되는 작업은 이 프로세스로부터 다음과 같습니다.

${\displaystyle W=\int _{V_{1}}^{V_{2}}P,dV.}$

(b2)

우리는 그 과정이 단열이어야 하므로, 다음 방정식은 참이어야 한다.

$(\displaystyle\Delta U+W=0)$

(b3)

이전 파생상품에 따르면

$({displaystyle PV^{\gamma}=text{constant}=P_{1}V_{1}^{\gamma}}).$

(b4)

재배치(b4)에 의해 제공됨

$({displaystyle P=P_{1}\left({\frac {V_{1}}{V}}\오른쪽)^{\gamma}}).$

이것을 (b2)에 대입하면 다음과 같은 결과가 나온다.

${\displaystyle W=\int _{V_{1}} {{2}} P_{1}\left({\frac {V_{1}} {V}}\right)^{\gamma},dV.}$

통합함으로써 우리는 일에 대한 표현을 얻는다.

${{displaystyle W=P_{1}V_{1}{\gamma}{\frac {V_{2}^{1-\gamma}}-V_{1}{1-\gamma}}}=bsfrac {P_{2}V_{1}-{1}{1-gamma}}:{1-}}$

두 번째 기간의 θ = α + 1/α로 치환하면,

$({displaystyle W=-\alpha P_{1}V_{1}^{\gamma}\left(V_{2}^{1-\gamma}-V_{1}^{1-\gamma}\right).}$

재배치,

$({displaystyle W=-\alpha P_{1}V_{1}\left(\frac {V_{2}}}{V_{1}}\오른쪽)^{1-\gamma }-1\오른쪽)}$

이상적인 가스 법칙을 사용하고 일정한 몰 양을 가정하면(실제적인 경우에서 종종 발생하는 경우),

$({displaystyle W=-\alpha nRT_{1}\left(\frac {V_{2}}}{V_{1}}\오른쪽)^{1-\gamma}-1\right).}$

연속식에 의해,

${{displaystyle {P_{2}}=\left({\frac {V_{2}}){V_{1}\오른쪽)^{-\gamma}}}$

또는

${\displaystyle\frac {P_{2}}{P_{1}}\오른쪽}^{-{\frac {1}{\frac }}=flac {V_{2}}{V_{1}}}}.}$

W의 이전 표현으로 대체하면,

${\displaystyle W=-\alpha nRT_{1}\left(\left(\frac {P_{2}}}\right)^{\frac {\frac -1}{\frac {\frac }}}-1\right}).}$

이 식과 (b3)의 (b1)을 대입하면 다음과 같이 된다.

$\displaystyle \alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\frac {P_{2}}{P_{1}\right)^{\frac {\frac - 1}{\fright}{\frac - {\frac - 1}}} {\fright} {\fright} {\frac } } } } } } } } } } } } 。}$

심플화,

${\displaystyle T_{2}-T_{1}=T_{1}\left(\frac {P_{2}}}{P_{1}}\오른쪽)^{\frac {\frac - 1}{\frac }{\fright}}{\frac - 1}}}}$

$(\displaystyle\frac{T_{2}}}{T_{1}}-1=\left({\frac {P_{2}}}{P_{1}}\오른쪽)^{\frac {\frac -1}{\frac }-1,}$

${\displaystyle T_{2}=T_{1}\left({\frac {P_{1}}\오른쪽)^{\frac {\frac -1}{\frac }.}$

이산 공식 및 작업 표현의 도출

상태 1에서 상태 2로 측정한 시스템의 내부 에너지 변화는 다음과 같습니다.

동시에, 압력-부피 변화에 의해 수행되는 작업은 이 프로세스로부터 다음과 같습니다.

${\displaystyle W=\int _{V_{1}}^{V_{2}}P,dV.}$

(c2)

우리는 그 과정이 단열이어야 하므로, 다음 방정식은 참이어야 한다.

$(\displaystyle\Delta U+W=0)$

(c3)

이전 파생상품에 따르면

$({displaystyle PV^{\gamma}=text{constant}=P_{1}V_{1}^{\gamma}}).$

(c4)

재배치(c4)에 의해 제공됨

$({displaystyle P=P_{1}\left({\frac {V_{1}}{V}}\오른쪽)^{\gamma}}).$

이것을 (c2)에 대입하면 다음과 같은 결과가 나온다.

${\displaystyle W=\int _{V_{1}} {{2}} P_{1}\left({\frac {V_{1}} {V}}\right)^{\gamma},dV.}$

통합함으로써 우리는 일에 대한 표현을 얻는다.

${{displaystyle W=P_{1}V_{1}{\gamma}{\frac {V_{2}^{1-\gamma}}-V_{1}{1-\gamma}}}=bsfrac {P_{2}V_{1}-{1}{1-gamma}}:{1-}}$

두 번째 기간의 θ = α + 1/α로 치환하면,

$({displaystyle W=-\alpha P_{1}V_{1}^{\gamma}\left(V_{2}^{1-\gamma}-V_{1}^{1-\gamma}\right).}$

재배치,

$({displaystyle W=-\alpha P_{1}V_{1}\left(\frac {V_{2}}}{V_{1}}\오른쪽)^{1-\gamma }-1\오른쪽)}$

이상적인 가스 법칙을 사용하고 일정한 몰 양을 가정하면(실제적인 경우에서 종종 발생하는 경우),

$({displaystyle W=-\alpha nRT_{1}\left(\frac {V_{2}}}{V_{1}}\오른쪽)^{1-\gamma}-1\right).}$

연속식에 의해,

${{displaystyle {P_{2}}=\left({\frac {V_{2}}){V_{1}\오른쪽)^{-\gamma}}}$

또는

${\displaystyle\frac {P_{2}}{P_{1}}\오른쪽}^{-{\frac {1}{\frac }}=flac {V_{2}}{V_{1}}}}.}$

W의 이전 표현으로 대체하면,

${\displaystyle W=-\alpha nRT_{1}\left(\left(\frac {P_{2}}}\right)^{\frac {\frac -1}{\frac {\frac }}}-1\right}).}$

이 식과 (c3)의 (c1)을 대입하면 다음과 같이 된다.

$\displaystyle \alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\frac {P_{2}}{P_{1}\right)^{\frac {\frac - 1}{\fright}{\frac - {\frac - 1}}} {\fright} {\fright} {\frac } } } } } } } } } } } } 。}$

심플화,

${\displaystyle T_{2}-T_{1}=T_{1}\left(\frac {P_{2}}}{P_{1}}\오른쪽)^{\frac {\frac - 1}{\frac }{\fright}}{\frac - 1}}}}$

$(\displaystyle\frac{T_{2}}}{T_{1}}-1=\left({\frac {P_{2}}}{P_{1}}\오른쪽)^{\frac {\frac -1}{\frac }-1,}$

${\displaystyle T_{2}=T_{1}\left({\frac {P_{1}}\오른쪽)^{\frac {\frac -1}{\frac }.}$

단열 그래프 작성

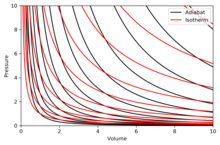
단열은 다이어그램에서 일정한 엔트로피의 곡선이다.P-V 다이어그램에 단열재의 몇 가지 특성이 표시되어 있습니다.이러한 특성은 양자 효과가 중요해지는 PV가 작아지는 영역(저온)을 제외하고 이상 기체의 고전적 행동에서 읽을 수 있다.

1. 모든 단열은 점근적으로 V축과 P축에 접근합니다(등온열과 같음).
2. 각 단열은 정확히 한 번 각 등온선과 교차한다.
3. 단, 확장 중에 단위는 등온선보다 더 많은 압력을 잃기 때문에 더 가파른 경사(더 수직)를 갖는다는 점을 제외하면 등온선과 유사합니다.
4. 등온선이 북동쪽으로 오목한 경우(45°), 단열선은 북동쪽으로 오목한 경우(31°)가 된다.
5. 단열과 등온도를 각각 엔트로피와 온도(윤곽선도상의 고도)의 일정한 간격으로 그리면 눈이 축 방향으로 이동하면서(남서쪽 방향) 등온도의 밀도는 일정하지만 단열밀도는 증가하는 것을 볼 수 있다.예외는 절대 0에 매우 가까우며, 단열체의 밀도가 급격히 떨어지고 희귀해집니다(네른스트의 ^[clarification needed]정리 참조).

오른쪽 다이어그램은 단열과 등온도가 중첩된 P-V 다이어그램입니다.

등온도는 빨간색 곡선이고 단위는 검은색 곡선입니다.

단열은 등엔트로피이다.

볼륨은 수평축이고 압력은 수직축입니다.

어원학

단열이라는 용어는 그리스어 ββαβββαα ο ο ο ο （ 강물의 크세노폰에 의해 사용됨)의 영어화이다.이것은 열역학적인 의미에서 ^[13][14]랭킨(1866)에 의해 사용되며, 1871년 맥스웰에 의해 채택되었다(명시적으로 ^[15]랭킨에 대한 용어).여기서 어원적 기원은 열로서의 에너지 전달과 벽을 통한 물질의 전달의 불가능에 해당합니다.

그리스어 ββα βα ο ο is priv priv τ βα " priv priv priv priv τ βα " " α α α α α α α α βα priv priv ^[16]priv priv priv priv priv priv priv priv priv priv priv priv priv priv priv priv priv priv priv the the the the the the the the from from the the the the the the

열역학 이론의 개념적 의미

단열 과정은 초기부터 열역학에서 중요했다.그것은 열과 일의 양을 거의 직접적으로 연관시키는 방법을 제공했기 때문에 줄의 작업에서 중요했다.

에너지는 열이나 작용으로만 질량 전달을 막는 벽으로 둘러싸인 열역학 시스템으로 들어가거나 나갈 수 있습니다.따라서 이러한 시스템의 작업량은 두 팔다리 주기의 동등한 열량과 거의 직접적으로 관련될 수 있습니다.첫 번째 사지는 시스템의 내부 에너지를 증가시키는 등산화 단열 작업 프로세스입니다.두 번째 사지는 등산화 열전달로 시스템을 원래 상태로 되돌립니다.따라서 랭킨은 열량 ^[17]측정이 아닌 작업 단위로 열의 양을 측정했습니다.1854년에 랭킨은 나중에 엔트로피라고 불리는 "열역학 함수"를 사용하였고, 그 당시 그는 "열의 전달이 없는 곡선"^[18]을 썼는데, 그는 나중에 단열 ^[13]곡선이라고 불렀다.두 개의 등온사지 외에 카르노 사이클은 두 개의 단열사지를 가지고 있다.

열역학의 기초에 있어서,^[19] 이것의 개념적 중요성은 브라이언,^[1] 카라테오도리, ^[20]그리고 보른에 의해 강조되었다.그 이유는 열량 측정이 열역학 제1법칙의 기술 이전에 이미 정의된 유형의 온도를 전제로 하기 때문입니다. 예를 들어 경험적 척도에 기초한 온도입니다.그러한 가정은 경험적 온도와 절대적 온도를 구별하는 것을 포함한다.오히려 절대 열역학적 온도의 정의는 제2법칙이 개념적 ^[21]기초로서 이용될 때까지 남겨두는 것이 가장 좋다.

18세기, 에너지 보존의 법칙은 아직 완전히 공식화되거나 확립되지 않았고, 열의 본질에 대해 논의되었다.이러한 문제에 대한 한 가지 접근법은 열량 측정으로 측정된 열을 양적으로 보존되는 주요 물질로 간주하는 것이었다.19세기 중반까지, 그것은 에너지의 한 형태로 인식되었고, 그로 인해 에너지 보존의 법칙도 인정되었다.에너지 보존의 법칙은 1차 공리이며 열은 그 결과로 분석되어야 한다는 것이 결국 확립되고 현재 옳다고 여겨지고 있다.이 관점에서 열은 상태 변수가 아니라 두 물체 간의 전달을 설명하는 변수이기 때문에 단일 물체의 총 에너지 구성 요소가 될 수 없습니다.단열 과정은 현재 ^[21]관점의 논리적 요소이기 때문에 중요하다.

단열이라는 단어의 다양한 용법

본 기사는 거시적 열역학 관점에서 작성되었으며, 단열이라는 단어는 랭킨이 소개한 전통적인 열역학 방식으로 이 글에서 사용되고 있다.본문에서는 예를 들어 기체의 압축 속도가 빠르면 기체가 단열적으로 일정한 벽에 의해 격리되지 않더라도 열전달이 일어날 시간이 거의 없다는 점을 지적하고 있다.이런 의미에서 기체의 빠른 압축은 종종 등엔트로픽과는 거리가 멀지만, 기체가 일정한 벽에 의해 단열적으로 격리되지 않은 경우에도 대략적으로 또는 느슨하게 단열이라고 합니다.

그러나 양자역학 및 양자통계역학에서는 단열이라는 단어를 매우 다른 의미로 사용합니다. 단열이라는 단어는 때때로 고전적인 열역학적인 의미와 거의 반대되는 것처럼 보일 수 있습니다.양자 이론에서 단열이라는 단어는 아마도 등엔트로픽에 가깝거나 아마도 준정적인 것을 의미할 수 있지만, 그 단어의 사용은 두 분야 사이에서 매우 다르다.

한편, 양자 이론에서, 압축 작업의 섭동 요소가 거의 무한히 느리게(즉, 준정적으로) 이루어지면, 그것은 단열적으로 이루어졌다고 한다.그 아이디어는 고유 함수의 모양이 천천히 그리고 지속적으로 변화하기 때문에 양자 점프가 트리거되지 않고, 그 변화는 사실상 가역적이라는 것이다.직업 수치는 변하지 않지만, 그럼에도 불구하고 일대일 대응, 압축 전 및 압축 후 고유 상태의 에너지 수준에 변화가 있다.따라서 섭동적인 작업 요소는 열 전달 및 시스템 내 랜덤 변화의 도입 없이 수행되었습니다.예를 들어 Max Born은 다음과 같이 쓰고 있습니다.실제로 이것은 우리가 해야 할 '단열'의 경우입니다.즉, 외부의 힘(또는 시스템 부분의 서로에 대한 반응)이 매우 느리게 작용하는 제한적인 경우입니다.이 경우, 매우 높은 근사치까지

${\displaystyle c_{1}^{2}=1,,,c_{2}^2}=0,,,,c_{3}^{2}=0,,,,,,,,,}$

즉, 전이 가능성은 없으며, 시스템은 섭동이 정지된 후 초기 상태에 있습니다.따라서 이러한 느린 섭동은 고전적으로 ^[22]볼 때 되돌릴 수 있습니다."

한편, 양자 이론에서, 압축 작업의 섭동 요소가 빠르게 이루어지면, 그것은 고유 상태의 직업 번호뿐만 아니라 모양도 임의로 변화시킨다.그 이론에서는 이러한 급격한 변화는 단열적이지 않다고 하며, 이에 반대되는 단어인 diabatic이 적용된다.아마도 클라우시우스가 이 문제에 직면했다면, 그가 당시에 사용했던 구식 언어로, "내부 작업"은 이루어졌고, "열은 전달되지 않았지만 생성되었다"^{[citation needed]}고 말했을 것이라고 추측할 수 있을 것이다.

또한 대기 열역학에서 디아바틱 과정은 열이 ^[23]교환되는 과정이다.

고전적인 열역학에서 이러한 급격한 변화는 여전히 단열이라고 불릴 것입니다. 왜냐하면 시스템은 단열적으로 격리되어 있고 열과 같은 에너지의 전달이 없기 때문입니다.점성 또는 기타 엔트로피 생성에 의한 변화의 강한 불가역성은 이러한 고전적인 사용에 영향을 미치지 않습니다.

따라서 거시 열역학에서 가스 덩어리의 경우, 시스템이 단열적으로 격리되지 않았더라도 압축이 열 전달을 피할 수 있을 만큼 빠르면 느슨하거나 대략적으로 단열이라고 말할 수 있을 정도로 단어가 사용됩니다.그러나 양자통계이론에서는 압축이 빠르면 단열이라고 부르지 않습니다.단열적으로 분리된 시스템이더라도 이 용어의 고전적인 열역학적인 의미에서는 단열이라고 할 수 없습니다.이 단어들은 위에서 말한 바와 같이 두 분야에서 다르게 사용된다.

「 」를 참조해 주세요.

• 파이어 피스톤
• 열폭발

관련 물리 토픽

• 열역학 제1법칙
• 엔트로피(고전 열역학)
• 단열 전도율
• 단열 감률
• 총기온
• 자기냉동
• 베리상

관련 열역학 프로세스

• 순환 과정
• 등압 과정
• 등각 과정
• 등엔트로픽 과정
• 아이소코릭법
• 등온 과정
• 폴리트로픽 과정
• 준정적 과정

레퍼런스

일반

• Silbey, Robert J.; et al. (2004). Physical chemistry. Hoboken: Wiley. p. 55. ISBN 978-0-471-21504-2.
• 네이브, 칼 로드 "단열 과정"하이퍼 물리
• 손그렌, 제인 R 박사.."단열 프로세스"Daphne – Palomar College Web Server, 1995년 7월 21일.2011-05-09년 Wayback Machine에 보관.

외부 링크

Wikimedia Commons의 단열 프로세스 관련 미디어

• 하이퍼물리학 백과사전 기사