전기망
Electrical network| 에 대한 기사 |
| 전자기학 |
|---|
 |
전기 네트워크는 전기 구성 요소(예: 배터리, 저항기, 인덕터, 캐패시터, 스위치, 트랜지스터) 또는 그러한 상호 연결의 모델로서 전기 요소(예: 전압 소스, 전류 소스, 저항, 인덕턴스, 캐패시턴스)로 구성된다.전기회로는 폐쇄회로(closed loop)로 구성된 네트워크로 전류에 대한 복귀 경로를 제공한다.선형 전기 네트워크는 선원(전압 또는 전류), 선형 덩어리 요소(저항기, 캐패시터, 인덕터), 선형 분산 요소(변속기 라인)로만 구성된 특수 유형으로 신호가 선형적으로 중첩될 수 있는 특성을 가지고 있다.따라서 라플라스 변환과 같은 강력한 주파수 영역 방법을 사용하여 DC 응답, AC 응답 및 과도 응답을 더 쉽게 분석한다.
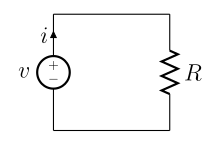
저항 회로는 저항기와 이상적인 전류 및 전압 공급원만 포함하는 회로다.저항성 회로 분석은 캐패시터와 인덕터를 포함하는 회로 분석보다 덜 복잡하다.선원이 일정한 (DC) 선원이면 그 결과는 DC 회로가 된다.임의 저항 네트워크의 유효 저항 및 전류 분배 특성은 그래프 측정 및 기하학적 특성에 따라 모델링할 수 있다.[1]
능동형 전자부품을 포함하는 네트워크를 전자회로라고 한다.그러한 네트워크는 일반적으로 비선형적이며 더 복잡한 설계와 분석 도구가 필요하다.
분류
수동성별
활성 네트워크는 네트워크에 에너지를 무한정 공급할 수 있는 최소한 하나의 전압 소스 또는 전류 소스를 포함한다.패시브 네트워크는 활성 소스를 포함하지 않는다.
활성 네트워크는 하나 이상의 기전력을 포함한다.그러한 출처의 실제적인 예로는 배터리나 발전기가 있다.활성 소자는 회로에 전원을 주입하고, 전력 이득을 제공하며, 회로 내의 전류 흐름을 제어할 수 있다.
수동형 네트워크는 어떤 기전력의 원천도 포함하지 않는다.그것들은 저항기와 콘덴서와 같은 수동적인 요소들로 구성되어 있다.
선형성별
네트워크는 그것의 신호가 중첩 원리를 따른다면 선형이고, 그렇지 않으면 비선형이다.패시브 네트워크는 일반적으로 선형 네트워크로 간주되지만 예외도 있다.예를 들어, 철심을 가진 인덕터는 충분한 전류를 가지고 구동할 경우 포화상태로 구동될 수 있다.이 영역에서 인덕터의 거동은 매우 비선형적이다.
뭉쳐서
이산형 패시브 구성품(저항기, 캐패시터, 인덕터)은 각각 저항, 캐패시턴스, 인덕턴스가 모두 한 곳에 ("점프") 있다고 가정하기 때문에 덩어리 원소라고 불린다.이러한 설계 철학을 집단 요소 모델과 네트워크라고 부르기 때문에 설계한 것을 집단 요소 회로라고 부른다.이것은 회로 설계에 대한 전통적인 접근방식이다.충분히 높은 주파수에서 또는 충분히 긴 회로(전력 송전 라인 등)에서, 구성 요소 치수에 걸쳐 파장의 상당 부분이 존재하기 때문에, 더 이상 일괄 가정은 유지되지 않는다.분산형 요소 모델이라 불리는 경우에 새로운 설계 모델이 필요하다.이 모델에 설계된 네트워크를 분산형 소자 회로라고 한다.
일부 덩어리 구성요소를 포함하는 분산 요소 회로를 반 덤프 설계라고 한다.세미 덤프 회로의 예로는 콤플라인 필터를 들 수 있다.
출처 분류
출처는 독립 출처와 종속 출처로 분류할 수 있다.
독립적
이상적인 독립 선원은 회로에 존재하는 다른 원소에 관계없이 동일한 전압 또는 전류를 유지한다.그것의 값은 일정(DC) 또는 사인파(AC)이다.전압이나 전류의 강도는 연결된 네트워크의 어떤 변화에도 불구하고 변하지 않는다.
종속적
종속 선원은 선원의 유형에 따라 전원 또는 전압 또는 전류를 전달하기 위한 회로의 특정 요소에 의존한다.
전기법 적용
많은 전기 법칙이 모든 선형 저항 네트워크에 적용된다.여기에는 다음이 포함된다.
- Kirchhoff의 현재 법률:노드로 들어오는 모든 전류의 합은 노드에서 나가는 모든 전류의 합과 같다.
- Kirchhoff의 전압 법칙:루프 주위의 전기적 전위차이의 지시된 합은 0이어야 한다.
- 옴의 법칙:저항기를 통과하는 전압은 저항의 산물 및 저항기를 통과하는 전류와 동일하다.
- 노턴의 정리:모든 전압 또는 전류 소스 및 저항기의 네트워크는 단일 저항기와 병렬로 이상적인 전류 소스와 전기적으로 동등하다.
- 테베닌의 정리:모든 전압 또는 전류 소스 및 저항기의 네트워크는 단일 저항기와 직렬로 구성된 단일 전압 소스와 전기적으로 동일하다.
- 중첩 정리:여러 개의 독립된 선원을 가진 선형 네트워크에서, 모든 선원이 동시에 작용하고 있을 때 특정 분기의 반응은 한 번에 하나의 독립 선원을 취함으로써 계산된 개별 응답의 선형 합과 같다.
이러한 법칙을 적용하면 대수학적으로 또는 수적으로 해결할 수 있는 일련의 동시 방정식이 발생한다.법률은 일반적으로 리액턴스를 포함하는 네트워크로 확장될 수 있다.그것들은 비선형 또는 시간 변동 요소를 포함하는 네트워크에서는 사용할 수 없다.
설계 방법
| 선형 네트워크 분석 | |
|---|---|
| 요소들 | |
| 구성 요소들 | |
| 직렬 및 병렬 회로 | |
| 임피던스 변환 | |
| 제너레이터 정리 | 네트워크 정리 |
| 네트워크 분석 방법 | |
| 2포트 매개변수 | |
아날로그 또는 디지털 전기 회로를 설계하려면 전기 엔지니어가 회로 내 모든 위치에서 전압과 전류를 예측할 수 있어야 한다.단순 선형회로는 복잡한 수 이론을 이용하여 손으로 분석할 수 있다.보다 복잡한 경우, 회로는 특화된 컴퓨터 프로그램 또는 조각-선형 모델과 같은 추정 기법으로 분석될 수 있다.
HSPIE(아날로그 회로 시뮬레이터)[2]와 같은 회로 시뮬레이션 소프트웨어와 VHDL-AMS, 베릴로그-AMS 등의 언어를 사용하면 엔지니어가 회로 프로토타입 제작에 수반되는 오류 위험, 시간, 비용 없이 회로를 설계할 수 있다.
네트워크 시뮬레이션 소프트웨어
보다 복잡한 회로는 SPICE나 GNUCAP와 같은 소프트웨어로 수치적으로 분석하거나, SapWin과 같은 소프트웨어를 사용하여 상징적으로 분석할 수 있다.
작동 지점 주변의 선형화
새로운 회로에 직면했을 때, 소프트웨어는 먼저 안정된 상태 해결책을 찾으려고 시도한다. 즉, 모든 노드가 Kirchhoff의 현재 법칙을 준수하고 회로의 각 요소를 통과하는 전압이 그 요소를 지배하는 전압/전류 방정식을 준수하는 것이다.
안정 상태 용액이 발견되면 회로 내 각 원소의 작동 지점을 알 수 있다.작은 신호 분석의 경우 모든 비선형 요소는 작동 지점 주위로 선형화하여 전압과 전류의 작은 신호 추정치를 얻을 수 있다.이것은 옴의 법칙을 응용한 것이다.결과 선형 회로 매트릭스는 가우스 제거를 통해 해결할 수 있다.
조각-선형 근사치
Simulink에 대한 FLECS 인터페이스와 같은 소프트웨어는 회로 요소를 지배하는 방정식의 조각-선형 근사치를 사용한다.이 회로는 이상적인 다이오드의 완전 선형 네트워크로 취급된다.다이오드가 켜짐에서 꺼짐 또는 그 반대로 전환될 때마다 선형 네트워크의 구성이 변경된다.방정식의 근사치에 더 많은 세부사항을 추가하면 시뮬레이션의 정확도가 증가하지만 실행 시간도 증가한다.
참고 항목
| Wikimedia Commons에는 전기 회로와 관련된 미디어가 있다. |
| 무료 사전인 Wiktionary에서 전기 회로를 찾아 보십시오. |
표현
설계 및 분석 방법론
측정
유사점
- 유압유추
- 기계적-전기적 유사점
- 임피던스 유추(맥스웰 유추)
- 모빌리티 유추(Firestone 유추)
- 전체 유추(트렌트 유추)
특정 위상
참조
- ^ Kumar, Ankush; Vidhyadhiraja, N. S.; Kulkarni, G. U . (2017). "Current distribution in conducting nanowire networks". Journal of Applied Physics. 122 (4): 045101. Bibcode:2017JAP...122d5101K. doi:10.1063/1.4985792.
- ^ "HSPICE" (PDF). HSpice. Stanford University, Electrical Engineering Department. 1999.