이산 미적분학

이산 미적분학 또는 이산함수의 미적분학은 증분 변화에 대한 수학적 연구로서 기하학이 형태에 대한 연구이고 대수학은 산술 연산의 일반화 연구와 같은 방식이다. 미적분이라는 단어는 원래 "작은 조약돌"이라는 뜻의 라틴어인데, 그러한 조약돌들이 계산에 사용되면서 그 의미가 진화했고 오늘날에는 대개 계산법을 의미한다. 한편 미적분학(minitimal miculus) 또는 "infinitimals의 미적분학(minitimals of infinitimals)"이라고 불리던 미적분학은 지속적인 변화를 연구하는 학문이다.

이산 미적분학에는 미분학과 적분이라는 두 가지 진입점이 있다. 미분학은 변화율의 증분율과 조각-직선 곡선의 기울기를 포함한다. 적분학은 수량의 축적과 조각-현상수 곡선 아래의 면적에 관한 것이다. 이 두 가지 관점은 이산 미적분의 근본적인 정리에 의해 서로 연관되어 있다.

변화의 개념에 대한 연구는 그 별개의 형태로부터 시작된다. 개발은 독립 변수의 증가$$ ${\displaystyle \Delta }$ x$${\$displaystyle \Delta$x} 매개 변수에 따라 달라진다. 만약 우리가 그렇게 선택한다면, 우리는 증분을 점점 더 작게 만들고 이러한 개념의 연속적인 상대들을 한계로 찾을 수 있다. $비공식적$으로 Δ x →${\displaystyle 0}$ ${\displaystyle \Delta$ x$\to$ 0$}$의 이산 $미적분 한계$는 최소$$ 미적분이다. 비록 그것이 미적분의 이산적 기초 역할을 하지만, 이산 미적분의 주요 가치는 응용에 있다.

두 개의 초기 구성

이산 미적분학은 함수의 정의, 속성 및 차이 인수의 적용에 대한 연구다. 차등지수를 구하는 과정을 분화라고 한다. 실제 선의 여러 지점에서 정의된 함수를 고려할 때, 그 지점에서의 차이 인수는 함수의 작은 척도(즉, 지점부터 다음 지점까지의) 동작을 인코딩하는 방법이다. 영역 내 연속된 점의 쌍마다 함수의 차이 지수를 찾아냄으로써, 차이 지수 함수 또는 원래 함수의 차이 지수라는 새로운 함수를 생산할 수 있다. 공식적 용어로, 차이 인수는 함수를 입력으로 삼고 두 번째 함수를 출력물로 생성하는 선형 연산자다. 이것은 함수가 보통 숫자를 입력하고 다른 숫자를 출력하는 초등 대수학에서 연구된 많은 과정보다 더 추상적이다. 예를 들어, 더블링 기능이 입력 3을 부여하면 6을 출력하고, 스퀴링 기능이 입력 3을 부여하면 9를 출력한다. 그러나 파생상품은 제곱 함수를 입력으로 받아들일 수 있다. 즉, 파생상품이 2를 4로 보내고, 3을 9로 보내고, 4를 16으로 보내고, 이 정보를 다른 기능을 생산하기 위해 사용한다. 스퀴링 기능을 차별화하여 생산되는 기능은 더블링 기능에 가까운 것으로 밝혀졌다.

함수가 x = > 0{\$displaystyle \Delta$ x$=h>0}$ 증분으로 구분된 지점에서 정의된다고 가정합시다

$a,a+h,a+2h,\ldots,a+nh,\ldots }$

"${\displaystyle \mathrm{더블링}}$ 함수"는$$ $g{\displaystyle }$( x${\displaystyle }$)${\displaystyle }$= 2 ${\displaystyle x}$ ${\displaystyle g(x)=2x},$ "스퀴링 함수"는 $f{\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle {x\mathrm{}}^{}}$ 2 ${\$로 나타낼 수 있다$.$ "차이 지수"는 다음 공식으로 정의된${\displaystyle }$[${\displaystyle x}$ ,${\displaystyle x}$+ ${\displaystyle h}$ ${\displaystyle ]}$ ${\displaystyle [x,x+h]$ 중 하나에 대한 함수의 변화율이다.

${\displaystyle {\frac {f(x+h)-f(x)}{h}.}$

그것은 기능 $f{\displaystyle }$ ${\displaystyle f}$을(를$$) 입력으로 가져간다. 즉, 2를 4로 보내고, 3을 9로 보내고, 4를 16으로 보내고, 이 정보를 사용하여 다른 $기능인{\displaystyle }$ g (${\displaystyle x}$)${\displaystyle }$= ${\displaystyle 2}$x + ${\displaystyle h}$를 출력한다$(\displaysty$ g$(x)=2x+h$ 편의상, 새로운 기능은 위의 구간의 중간 지점에서 정의될 수 있다.

${\displaystyle a+h/2,a+h+h+h/2,a+2h+h/2,a+2h+h/2,a+nh+h/2,...}$

변화율은 전체 구간${\displaystyle }$[${\displaystyle x,}$ ${\displaystyle x}$+ ${\displaystyle h}$ ${\displaystyle ]}$ ${\displaystyle [x,x+h]}$에 대한 변화율이기 때문에$,$ 그 안에 있는 어떤 지점도 그러한 참조로 사용할 수 있고, 심지어 차이를 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$ -cochain으로 만드는 전체 구간으로 사용할 수 있다.

차이 인수에 대한 가장 일반적인 표기법은 다음과 같다.

${\displaystyle {\frac {\Delta f}{\Delta x}}(x+h/2)={\frac {f(x+h)-f(x)}{h}.}$

함수의 입력이 시간을 나타내는 경우, 시간에 대한 차이를 나타내는 몫은 변화를 나타낸다. 예를 들어, $f{\displaystyle }$ ${\displaystyle f}$이(가) 입력으로서 시간을 소요하고 그 시간에 공의 위치를 출력하는 $함수$라면,$$f {\$displaystyle$f}의 차이점 지수는 시간이 지남에 따라 위치가 어떻게 변화하고 있는지$$, 즉 공의 속도다.

함수가 선형인 경우(즉, 함수의 그래프 포인트가 직선에 있으면), 함수는 $y{\displaystyle }$= m ${\displaystyle x}$+ b ${\displaystyle y=mx+b}$로 기록할 수 있다$.$ $여기$서 x ${\$$displaystyle$ y$}$은 독립$$ 변수, y ${\$displaysty y$}$은 종속 변수, b ${\displaysty}$은 y = ${\dplay$$aystyle y}$ -reason$$ 및:

${\displaystyle m={\frac {\text{rise}{\text{run}}}={\frac {{\text{changes in }}}{}}}{\frac}}}{\frac {{\frac {\Delta y}{delta x}}}}}.}$

이것은 직선의 기울기에 정확한 값을 준다.

그러나 함수가 선형적이지 않으면 $y{\displaystyle }$ ${\displaystyle y}$의 변경 사항을 $x{\displaystyle }$ ${\displaystyle x}$의 변경으로 나눈$$ 값이 달라진다$$. 차이 인수는 입력의 변화에 관한 산출물의 변화 개념에 정확한 의미를 부여한다. 구체적으로는 $f{\displaystyle }$ ${\displaystyle f}$을(를) 함수로 하고$$$,{\displaystyle }$ $f{\displaystyle }$ ${\displaystyle \{\backslash }$$displaystyle$ f$\}$의 ${\displaystyle \mathrm{도메인}}$에서$점 x {\displaystyle$ x${\displaystyle \}}$을$($를${\displaystyle )}$ 고정하는 것이$$ $함수$ $그래프상의{\displaystyle }$ 점이다. $h{\displaystyle }$ ${\displaystyle h}$이$($가) $x{\displaystyle }$ ${\displaystyle x}$의 증분인$$ 경우 $x{\displaystyle }$+ ${\displaystyle h}$ ${\displaystyle x$$+h$$}$의 다음 $값$이 된다$.$ 따라서${\displaystyle }$( ${\displaystyle x}$+ ${\displaystyle h}$, ${\displaystyle f}$( ${\displaystyle x}$+ h$){\displaystyle (x+h,f(x+h)}}$은(${\displaystyle x,}$ ${\displaystyle f}$($){\displaystyle (x,f(x)})$의 증분이다$.$ 이 두 점 사이의 선의 기울기는

${\displaystyle m={\frac {f(x+h)-f(x)}{{(x+h)-x}}={\frac {f(x+h)-f(x)}}.}$

따라서 $m{\displaystyle }$ ${\$$displaystyle$ $m}$은$($${\displaystyle x,}$ ${\displaystyle f}$( ${\displaystyle x}$ ) $displaystyle(x,f(x$$)}$과$($의 선의 기울기다$.$

여기 제곱 함수의 차이 지수인 특별한 예가 있다. $f{\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$을 제곱 함수로 한다$$. 다음:

${\displaystyle {\begin{aligned}{\frac {\Delta f}{\Delta x}}(x)&={(x+h)^{2}-x^{2} \over {h}}\\&={x^{2}+2hx+h^{2}-x^{2} \over {h}}\\&={2hx+h^{2} \over {h}}\\&=2x+h.\end{정렬}}}$

차액지수의 차액지수를 두 번째 차액지분이라고 하며 다음과 같이 정의한다.

${\displaystyle a+h,a+2h,a+3h,\ldots,a+nh,\ldots }$

등등.

이산 적분학은 리만 합계의 정의, 속성 및 응용에 대한 연구다. 합계의 가치를 찾아내는 과정을 통합이라고 한다. 기술 언어에서 적분학은 특정 선형 연산자를 연구한다.

Riemann sum은 함수를 입력하여 함수를 출력하는데, 입력 그래프 부분과 x 축 사이의 영역의 대수적 합을 제공한다.

동기부여가 되는 예는 주어진 시간 동안 이동한 거리들이다.

${\displaystyle {\text{distance}={\text{speed}\cdot {\text{time}}}$

속도가 일정하다면 곱셈만 필요하지만 속도가 변하면 여러 짧은 간격으로 시간을 쪼개서 이동한 거리를 평가한 다음, 각 간격에서 경과한 시간에 그 간격의 속도 중 하나를 곱한 다음, 각 간격에서 이동한 거리의 합계(리만 합)를 취한다.

속도가 일정할 경우 주어진 시간 간격에 걸쳐 이동한 총 거리는 속도와 시간을 곱하여 계산할 수 있다. 예를 들어, 3시간 동안 시속 50마일을 꾸준히 여행하면 총 거리는 150마일이 된다. 왼쪽의 도표에서 등속과 시간을 그래프로 나타낼 때 이 두 값은 경과된 시간과 동일한 속도와 너비가 있는 직사각형을 형성한다. 따라서 속도와 시간의 산물은 속도 곡선 아래의 직사각형 영역도 계산한다. 곡선 아래 영역과 이동 거리 사이의 이러한 연결은 주어진 시간 동안 점진적으로 변화하는 속도를 나타내는 불규칙한 형태로 확장될 수 있다. 오른쪽 다이어그램의 막대가 간격마다 다른 속도를 나타내는 경우 이동 거리$({\displaystyle a}$와 $b{\displaystyle }$ ${\displaystyle b$로 표시된 시간 사이)는$$음영 영역 s {\displaystyle $s}$의 영역이다$.$

$따라서{\displaystyle }$ ${\displaystyle a}$과(와) $b{\displaystyle }$ ${\displaystyle b}$ 사이의 간격은 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle x}$ ${\displaystyle \Delta$x$}$기호로 표시되는 각 세그먼트의 길이와 동일한 세그먼트로 나뉜다$$$.$ 각 작은 세그먼트에 대해 $함수{\displaystyle }$ f${\displaystyle }$( ${\displaystyle x}$) ${\displaystystyle f(x)$의 값이 하나씩 있다$.$ $v{\displaystyle }$ ${\displays$.$v}$을(를) 강조하다$.$ 그런 다음 기본 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle x}$ ${\displaystyle \Delta x}$ 및 $높이$ v ${\displaystyle v}$이(가) 있는 사각형의 영역은 해당 세그먼트에서 이동한 거리(${\displaystyle \Delta }$ x ${\displaystyle \Delta x}$에 속도 $v{\displaystyle }$ ${\displaystyty v}$ 곱한 시간)를 제공한다$.$ 각 세그먼트와 ${\displaystyle \mathrm{연관}}$되어 $f{\displaystyle }$( x${\displaystyle }$)${\displaystyle }$= ${\displaystyle v}$ ${\displaystyle f(x)=v}$ 위에 있는 함수의 값이다$.$ 이러한 모든 직사각형의 합은 축과 조각-현상수 곡선 사이의 면적을 제공하며, 이는 총 이동 거리인 것이다.

길이가 같은 = h > ${\displaystyle \Delta x=h>0}$인 구간의 중간점에 함수가 정의된다고 가정합시다

${\displaystyle a+h/2,a+h+h+h/2,a+2h+h/2,\ldots,a+nh-h/2,\ldots }$

시그마 표기법에서 ${\displaystyle a}$에서${\displaystyle }b{\displaystyle }$ =${\displaystyle }$+ ${\displaystyle n}$ h ${\displaystyle b=a+nh}$까지의 리만 합은 다음과 같다.

${\displaystyle \sum _{i=1}^{nf(a+ih)\,\Delta x.}$

이 계산은 각 $n{\displaystyle }$ ${\displaystyle n}$에 대해 수행되므로 새 함수는 다음 지점에서 정의된다$.$

$a,a+h,a+2h,\ldots,a+nh,\ldots }$

미적분학의 기본 정리는 미분화와 통합이 역연산이라고 명시하고 있다. 더 정확히 말하면, 그것은 리만 합계에 대한 차이 인수를 연관시킨다. 분화가 통합의 역행이라는 점을 정확히 밝힌 것으로도 해석할 수 있다.

미적분의 기본 정리: 함수 $f{\displaystyle }$ ${\$$displaystyle$ $f}$이(가) 구간$[, b$의 파티션에 정의되어$$ 있고$,$ $b{\displaystyle }$${\displaystyle }$=${\displaystyle }$+${\displaystyle n}$ h ${\displaystyle b=a+nh$ F ${\displaystyle F}$이(가) $차이{\displaystyle }$ 지수가 f ${\displaystystyle f}$인 함수라면$$, 우리는 다음을 가진다$.$

${\displaystyle \sum _{i=0}^{n-1f(a+ih+h/2)\,\Delta x=F(b)-F(a).}$

또한 모든 $m$= $0,$ $1$, 2,$\dots ,$ $\mathrm{n}$- 1 ${\textstyle m=0,1,2,\ldots,n-1$에 대해 다음을 수행하십시오.

${\displaystyle {\frac {\Delta }{\Delta x}\sum _{i=0}^{m}f(a+ih+h/2)\\\Delta x=f(a+mh+h+h/2)\\Delta x=f(a+mh+h+h/2)2.}$

이것은 또한 차이 방정식의 원형 해결책이다. 차이 방정식은 알 수 없는 함수와 차이 또는 차이 인수를 연관시키며, 과학에서 어디에나 존재한다.

역사

이산 미적분의 초기 역사는 미적분의 역사다. 차이 인용구와 리만 합계와 같은 기본적인 생각은 정의와 증명에서 암묵적으로 또는 명시적으로 나타난다. 그러나 한도를 취한 후에는 다시는 볼 수 없게 된다. 그러나 키르쇼프의 전압법(1847년)은 1차원 이산형 외부파생물의 관점에서 표현할 수 있다.

20세기 동안 이산 미적분은 미적분학 특히 미분학과는 상호 연관되어 있지만 둘 다 발달함에 따라 대수적 위상에서부터 끌어오기 시작한다. 주요 기여금은 다음과 같은 개인에서 나온다.^[1]

• 앙리 푸앵카레: 삼각측량(이심분할, 이중삼각측량), 푸앵카레 보조정리, 일반 스톡스 정리(Stokes Organization)의 첫 번째 증빙서, 그리고 훨씬 더 많은 것.
• L. E. J. 브루어: 단순 근사 정리
• 엘리 카탄, 조르주 드 람: 차동 형태의 개념, 좌표 독립적인 선형 연산자로서의 외부 파생 모델, 형태 정확성/폐쇄성
• 에미 노에더, 하인츠 홉프, 레오폴드 비토리스, 발터 메이어: 체인 모듈, 경계 연산자, 체인 콤플렉스
• J. W. 알렉산더, 솔로몬 렙체츠, 레프 폰트랴긴, 안드레이 콜모고로프, 노먼 스텐로드, 에두아르 체흐: 초기 코체인 개념
• 헤르만 바일: Kirchhoff 법은 경계와 공동 경계 연산자의 관점에서 명시되어 있다.
• W. V. D. 호지: 호지 항성 연산자, 호지 분해
• 새뮤얼 에일렌버그, 선더스 맥 레인, 노먼 스틴로드, J.H.C. 화이트헤드: 체인과 코체인 콤플렉스를 포함한 호몰로지 및 코호몰로지 이론의 엄격한 개발, 컵 제품
• Hassler Whitney: 통합업체로 협력

휘트니를 시작으로 하는 이산 미적분학의 최근 발전은 응용 모델링의 필요성에 의해 추진되어 왔다.^[2][3][4]

적용들

이산 미적분은 물리과학, 보험수리적 과학, 컴퓨터 과학, 통계학, 공학, 경제학, 사업, 의학, 인구통계학, 그리고 문제를 수학적으로 모델링할 수 있는 모든 분야에서 미적분학의 소산으로서 직간접적으로 모델링하는데 사용된다. 그것은 한 사람이 (비정규적인) 변화율에서 전체 변화로, 또는 그 반대로 갈 수 있도록 하며, 우리가 아는 문제를 연구하면서 다른 문제를 찾으려고 하는 경우가 많다.

물리학은 미적분을 특히 이용한다; 고전 역학과 전자석의 모든 이산 개념은 이산 미적분을 통해 연관된다. 점증적으로 변화하는 알려진 밀도의 물체의 질량, 그러한 물체의 관성 모멘트, 그리고 분리된 보수적 분야 내에서 물체의 총 에너지는 이산 미적분학을 사용하여 찾을 수 있다. 역학에서 이산 미적분학을 사용하는 예로는 뉴턴의 두 번째 운동 법칙이 있다: 역사적으로 그것은 신체의 운동량의 변화는 신체에 작용하는 결과적인 힘과 같으며 같은 방향에 있다는 차이 인수를 내포하고 있는 "운동의 변화"라는 용어를 명시적으로 사용한다고 한다. 오늘날 일반적으로 힘 = 질량 × 가속으로 표현되며, 가속도는 공간 위치의 시간 또는 두 번째 차이 인수에 관한 속도의 차이 지수이기 때문에 변화가 증분할 때 이산 미적분을 호출한다. 물체가 어떻게 가속하고 있는지 아는 것에서부터 시작해서, 우리는 리만 합계를 사용하여 그 경로를 도출한다.

맥스웰의 전자기학 이론과 아인슈타인의 일반 상대성 이론은 이산 미적분학의 언어로 표현되었다.

화학은 반응률과 방사능 붕괴를 결정하는 데 미적분학을 사용한다.

생물학에서 인구 역학은 인구 변화를 모형화하기 위한 재생산과 사망률에서 시작된다(인구 모델링).

공학에서 차이 방정식은 무중력 환경 내에서 우주선의 항로를 그리고 열 전달, 확산 및 파동 전파를 모형화하는 데 사용된다.

그린의 정리의 이산 아날로그는 평면측정기로 알려진 계측기에 적용되는데, 도면에 평평한 표면의 면적을 계산하는 데 사용된다. 예를 들어, 그것은 불규칙한 모양의 화단이나 수영장이 건물의 배치도를 설계할 때 차지하는 면적의 양을 계산하는 데 사용될 수 있다. 그것은 영상의 직사각형 도메인 합계를 효율적으로 계산하고, 형상을 신속하게 추출하고 물체를 검출하는데 사용될 수 있는 또 다른 알고리즘은 총 면적 표이다.

의학의 영역에서는 미적분을 이용하여 혈관의 최적 가지각도를 찾아 혈류를 최대화할 수 있다. 특정 약물이 몸에서 제거되기 위한 부패법칙으로부터, 투약법을 도출하는 데 사용된다. 핵의학에서는 표적 종양요법에서 방사선 수송 모델을 만드는 데 사용된다.

경제학에서 미적분학은 시장 모델링뿐만 아니라 한계비용과 한계수익을 모두 계산하여 최대 이익의 결정을 가능하게 한다.^[5]

이산 미적분은 다른 수학적 학문들과 함께 사용될 수 있다. 예를 들어, 확률 이론에서 가정된 밀도함수로부터 이산 랜덤 변수의 확률을 결정하는 데 사용될 수 있다.

차이 및 합계의 미적분학

함수($0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$ -cochain$$) $f{\displaystyle }$ ${\displaystyle f}$이(가) 증가 = > 0 ${\displaystyle \Delta x=h>0$ :로 구분된 점에서 정의된다고$$ 가정합시다.

$a,a+h,a+2h,\ldots,a+nh,\ldots }$

함수의 차이(또는 외부 파생상품 또는 공동경계 연산자)는 다음과 같다.

${\displaystyle {\big (}\Delta f{\big )}{\big (}[,x+h]{\big )}=f(x+h)-f(x).}$

위의 각 간격마다 정의되며, $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$ -cochain이다$$.

$위$의 각 간격마다 1 ${\displaystyle 1}$ $-cochain$ g ${\displaystyle g}$이(가) 정의된다고 가정해 보십시오. 그리고 그 합계는 다음과 같이 각 점에서 정의된 함수($0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$ -cochain$$)이다.

${\displaystyle \left(\sum g\right)\!(a+nh)=\sum _{i=1}^{ng{n}g(}[a+(i-1)h,a+ih]{\big )}.}$

이러한 속성은 다음과 같다.

• 상수 규칙: $c{\displaystyle }$ ${\displaystyle c}$이(가) 상수인 경우

${\displaystyle \Delta c=0}$

• 선형성: ${\displaystyle a}$ 및 $b$ ${\displaystyle b}$이(가) 상수인 경우

$\displaystyle \Delta (af+bg)=a\,\Delta f+b\,\Delta g,\quad \sum (af+bg)=a\,\sum f+b\,\sum g}$

• 제품 규칙:

$(\displaystyle \Delta (fg)=f\,\Delta g+g\,\Delta f\,\Delta g}$

• 미적분 1의 기본 정리:

$\displaystyle \left(\sum \Delta f\right)\!(a+nh)=f(a+nh)-f(a)}$

• 미적분 II의 기본 정리:

$[\displaystyle \Delta \!\왼쪽(\sum g\오른쪽)=g}$

이 정의는 다음과 같이 그래프에 적용된다. 그래프 노드에서 함수($0{\displaystyle \mathrm{}}$ ${\displaystyle 0$} -cochain$$) $f{\displaystyle }${\$displaystyle f}$이(가) 정의된 경우:

$a,b,c,\ldots }$

그 다음에는 외부 파생 모델(또는 차등)이 차이, 즉 그래프 가장자리에 정의된 다음 함수(${\displaystyle \mathrm{}}$ ${\displaystyle 1}$ -cochain$$)가 된다.

$왼쪽(df\오른쪽)\!{\big (}a,b]{\big )}=f(b)-f(a).}$

$g{\displaystyle }$ ${\displaystyle g}$이(가) $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$ -cochain인$$ 경우, 그래프의 일련의$$ 에지 위에 통합된 그래프는 $\sigma {\displaystyle }$ ${\displaystyle \sigma$$}("$$$경로 적분)의 모든 에지에 대한 값의 합이다.

${\displaystyle \int _{\putma }g=\sum _{\putma }g{\big (}a,b]{\big )}.}$

다음은 속성:

• 상수 규칙: $c{\displaystyle }$ ${\displaystyle c}$이(가) 상수인 경우

${\displaystyle dc=0}$

• 선형성: ${\displaystyle a}$ 및 $b$ ${\displaystyle b}$이(가) 상수인 경우

${\displaystyle d(af+bg)=a\,df+b\,dg,\nt \int _{\ftma }}(af+bg)=a\,\int _{\f+bma }g}$

• 제품 규칙:

${\displaystyle d(fg)=f\,dg+g\,df+df\,dg}$

• Fundamental theorem of calculus I: if a ${\displaystyle 1}$-chain ${\displaystyle \sigma }$ consists of the edges ${\displaystyle [a_{0},a_{1}],[a_{1},a_{2}],...,[a_{n-1},a_{n}]}$, then for any ${\displaystyle 0}$-cochain ${\displa$$ystyle f}$

${\displaystyle \int _{\fma }df=f(a_{n}-f(a_{0})}$

• 미적분 II의 기본 정리: 그래프가 나무인 경우 $g{\displaystyle }$ ${\displaystyle g}$은(는) $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$ -cochain이고$$ 함수(${\displaystyle \mathrm{}}$ ${\displaystyle 0}$ -cochain$$)는 그래프 노드에 다음과 같이 정의된다.

${\displaystyle f(x)=\int _{\putma }g}$

where a ${\displaystyle 1}$-chain ${\displaystyle \sigma }$ consists of ${\displaystyle [a_{0},a_{1}],[a_{1},a_{2}],...,[a_{n-1},x]}$ for some fixed ${\displaystyle a_{0}}$, then

$(\displaystyle df=g}$

참조를 참조하십시오.^{[6][7][8][9][3][10]}

단순화 및 큐브 체인

단순 콤플렉스 $S{\displaystyle }$ ${\displaystyle$ S$}$는 다음과 같은 조건을 만족하는 단순화 집합이다.

1. $S{\displaystyle }$ ${\displaystyle S}$의 심플렉스 각 면도 S$$ ${\displaystyle$ S$}$에 $있다.$

2. $\sigma {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle S}$ ${\displaystyle \sigma _{1},\sigma _{2}\in S}$의 두 가지 단순함의 비어 있지 않은 교차점은 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ ${\displaystyle {\sigma \mathrm{}}_{}}$ 2 ${\$ \sigma $_{$2}}의 면이다$.$

정의에 따르면 k-simplex의${\displaystyle }$방향은${\displaystyle {}_{}}$(${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{},}$ . . . . , ${\displaystyle v_{}}$ k${\displaystyle {}_{}}$) ${\displaystyle (v_{0},$ ...,$v_{k$로 쓰여진 정점의 순서에 의해 주어지며, 두 순서가 동일한 순열인 경우에만 동일한 방향을 정의한다는 규칙이다. 따라서 모든 심플렉스에는 정확히 두 개의 방향이 있고, 두 꼭지점의 순서를 바꾸면 반대 방향으로 방향이 바뀐다. 예를 들어, 1-심플렉스 방향을 선택하는 것은 가능한 두 가지 방향 중 하나를 선택하는 것과 같고, 2-심플렉스 방향을 선택하는 것은 "시계 반대 방향"이 무엇을 의미해야 하는지를 선택하는 것과 같다.

$S{\displaystyle }$ ${\displaystyle S}$을(를) 단순한 복합체가 되도록$$ 하자. 단순 k-체인(simplemental k-chain)은 한정된 공식 금액이다.

${\displaystyle \sum _{i=1}^{N}c_{i}\sigma _{i}\,}$

여기서 각 c는_i 정수, σ은_i 지향적인 k- orientedx이다. 이 정의에서 우리는 각 방향의 심플렉스(simplex)가 반대 방향의 심플렉스(simplex)의 음과 동일하다고 선언한다. 예를 들어,

${\displaystyle (v_{0},v_{1}}=-(v_{1},v_{0}).}$

$S{\displaystyle }$ ${\displaystyle S}$에 k-chains의 벡터 $공간$은 ${\displaystyle C_{}}$ k$${\$displaystyle C_{k}$라고 쓰여 있다$.$ $S{\displaystyle }$ ${\displaysty S}$에 있는 k-simplices 집합과 일대일 대응의 근거를 가지고 있다$.$ 근거를 명시적으로 정의하려면 각 심플렉스 방향을 선택해야 한다. 이를 위한 한 가지 표준 방법은 모든 정점의 순서를 선택하고 정점의 유도 순서에 해당하는 방향을 각 정점의 순서에 따라 심플렉스에게 부여하는 것이다.

$\sigma {\displaystyle }$=${\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$. .${\displaystyle }$. , v ${\displaystyle k_{}}$) ${\displaystyle \sigma =(v_{0},$ ...,$v_{k}}}$은(는) ${\displaystyle C_{}}$ k ${\$$k}$의 기본 요소로 간주되는 방향 k-심플렉스$$. 경계 연산자

$\displaystyle \property _{C_{k}\오른쪽 화살표 C_{k-1}$

선형 연산자는 다음과 같이 정의된다.

${\displaystyle \property_{k}}=\sum _{i=0}^{k(1)^{i}(v_{0},\widehat {v_{i}}},\widehat {v_{i}}},\data,v_{k}),}}$

지향적인 심플렉스

${\displaystyle(v_{0},\filename, {\widehat {v_{i}}},\filename,v_{k}}}}$

$i{\displaystyle }$ ${\displaystyle$ i$}$의 정점을 삭제하여 얻은$$$obtained{\displaystyle }$ ${\displaystyle \sigma}$의 면 i$$ ${\displaystyle$ i$}$이다.

${\displaystyle C_{}}$ k ${\$에서$$부분군 원소

${\displaystyle Z_{k}=\ker \partial _{k}}$

주기 및 부분군이라고 한다.

${\displaystyle B_{k}=\operatorname {im} \partial _{k+1}}$

경계로 이루어져 있다고 한다.

직접적인 계산에 의하면 $\partial {\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$= ${\displaystyle 0}$ ${\displaystyle \partial ^{2}=0$ 기하학적 용어로 이것은 어떤 것의 경계도 경계가 없다고 한다. 동등하게 벡터 공간$({\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ,${\displaystyle {\mathrm{}}_k}$ k${\displaystyle {}_{}}$) ${\displaystyle (C_{k},\partial _{k})$은 체인 콤플렉스를 형성한다. ${\displaystyle {Bk}_{}}${\$displaystyle B_{k$}}이(가$)$$$ k {\$displaystyle$ Z_${k}$에 포함되어 있다는$$ 다른 동등한 진술도 있다$.$

입체복합체란 점, 선 세그먼트, 정사각형, 정사각형, 그리고 그 n-차원적 복합체로 구성된 집합체다. 그것들은 콤플렉스를 형성하기 위한 단순화에 유사하게 사용된다. 기본 간격은 폼의 하위$$ 집합 $I{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle R\mathbf{}}$ ${\$입니다.

${\displaystyle I=[\ell ,\ell +1]\quad {\text{or}}\quad I=[\ell ,\ell ]}$

일부 ${\displaystyle \ell \mathbf{}}${$$Z {\$displaystyle \ell$\in $\mathbf$ {$Z} }$에 대해$.$ 기본 큐브 $Q{\displaystyle }$ ${\displaystyle Q}$는 기본 간격의 유한 제품이다.

${\displaystyle Q=I_{1}\time I_{2}\time \cdots \time I_{d}\subset \mathbf {R}^{d}}}}}$

여기서 $I{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{I\mathrm{}}_{}}$ 2,${\displaystyle \dots ,}$ I ${\displaystyle d_{}}$ ${\$는 기본 간격이다$$. Equivalently, an elementary cube is any translate of a unit cube ${\displaystyle [0,1]^{n}}$ embedded in Euclidean space ${\displaystyle \mathbf {R} ^{d}}$ (for some ${\displaystyle n,d\in \mathbf {N} \cup \{0\}}$ with ${\displaystyle n\leq d}$). 세트 $X{\displaystyle }$ ${\displaystyle \subseteq }$ ${\displaystyle {\mathbf{}}^{}}$ ${\displaystyle {}^{}}$ ${\$^{$d}}}$는 기본 큐브의 조합으로 쓸 수 있다면(또는 그러한 세트에 대해 동형일 가능성이 있는 경우) 입체복합체로서, 큐빅의 모든 면을 포함하고 있다. 경계 운영자와 체인 단지는 단순화 단지와 유사하게 정의된다.

더 일반적인 것은 세포 복합체들이다.

A chain complex ${\displaystyle (C_{*},\partial _{*})}$ is a sequence of vector spaces ${\displaystyle \ldots ,C_{0},C_{1},C_{2},C_{3},C_{4},\ldots }$ connected by linear operators (called boundary operators) ${\displaystyl$$e \reason _{n}:$$C_{n}\to C_{n-1},$ 즉 연속 2개의 지도 구성이 영도(zero map)가 되도록 한다$.$ 명시적으로 경계 연산자는 $\partial {\displaystyle {\mathrm{}}_n}$ ${\displaystyle {\mathrm{}}_n}$∂n + ${\displaystyle 1_{}}$= ${\displaystyle 0}$ ${\displaystyle \partial _{n}\circle \partial _{n+1}=0$을(를) 만족하거나$,{\displaystyle {\mathrm{}}^{}}$ 지수를 ${\displaystyle {억제}^{}}$한${$ = 0 {\$displaystyle \partial$^{2}=$0}$을 만족한다$.$ 단지는 다음과 같이 기재할 수 있다.

${\displaystyle \cdots {\xleftarrow {\partial _{0}}}C_{0}{\xleftarrow {\partial _{1}}}C_{1}{\xleftarrow {\partial _{2}}}C_{2}{\xleftarrow {\partial _{3}}}C_{3}{\xleftarrow {\partial _{4}}}C_{4}{\xleftarrow {\partial _{5}}}\cdots }$

심플렉스 지도는 심플렉스 정점의 이미지가 항상 심플렉스(따라서 정점은 이미지 정점을 가지고 있다)에 걸쳐 있는 속성을 가진 단순 콤플렉스 사이의 지도다. 단순 콤플렉스 $S{\displaystyle }$ ${\displaystyle S}$에서 $다른{\displaystyle }$ T ${\displaystyle T}$까지의 단순 지도 $f{\displaystyle }$ ${\displaystyle f}$는 $S{\displaystyle }$ ${\displaystyle$ $S}$의 정점 집합에서$$ $S{\displaystyle }$ ${\displaystyty$ $T}$의 정점 집합으로 표시되는 각 심플렉스 영상이다$$.$$ $T{\displaystyle }$ ${\$$displaystyle T}$의 심플렉스$.$ $체인{\displaystyle }$ 맵이라고 불리는 S {\$displaystyle$ S$}$의 $체인{\displaystyle }$콤플렉스에서 T {\$displaystyle$ T}의 체인 콤플렉스에 이르는$$ 선형 맵을 생성한다$.$ 명시적으로 $K{\displaystyle }$ ${\displaystyle k}$ -chains에$$ 주어진다.

${\displaystyle f(v_{0},\ldots,v_{k})=(f(v_{0}),\ldots,f(v_{k})}}$

$f$${\displaystyle }$( ${\displaystyle {v\mathrm{}}_{}}$ $0$$$)${\displaystyle }$,${\displaystyle }$.${\displaystyle }$. . . . .${\displaystyle {}_{}}$. . . . .${\displaystyle }$. . . . . . . . . .$$. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$$. . . . . . . . . . . . . . . . . . . . .$$. . . $.$ . . . . . . . . .

A chain map ${\displaystyle f}$ between two chain complexes ${\displaystyle (A_{*},d_{A,*})}$ and ${\displaystyle (B_{*},d_{B,*})}$ is a sequence ${\displaystyle f_{*}}$ of homomorphisms ${\displaystyle f_{n}:$$A_{n}\rightarrow B_{n}}$ for each ${\displaystyle n}$ that commutes with the boundary operators on the two chain complexes, so ${\displaystyle d_{B,n}\circ f_{n}=f_{n-1}\circ d_{A,n}}$. This is written out in the following commutative diagram:

체인 맵은 사이클을 사이클로, 경계를 경계로 보낸다.

참조를 참조하십시오.^{[11] [10] [12]}

이산형 차동형식: 코인

For each vector space C_i in the chain complex we consider its dual space ${\displaystyle C_{i}^{*}:=\mathrm {Hom} (C_{i},{\bf {R}}),}$ and ${\displaystyle d^{i}=\partial _{i}^{*}}$ is its dual linear operator

${\displaystyle d^{i-1}:C_{i-1}^{*}^\to C_{i}^{*}.}$

이는 코체인 콤플렉스를 남기면서 원래 콤플렉스의 '모든 화살표를 뒤집는다'는 효과가 있다.

${\displaystyle \cdots \leftarrow C_{i+1}^{*}{\stackrel {\partial _{i}^{*}}{\leftarrow }}\ C_{i}^{*}{\stackrel {\partial _{i-1}^{*}}{\leftarrow }}C_{i-1}^{*}\leftarrow \cdots }$

코체인 콤플렉스$({\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$, ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$) ${\displaystyle (C^{*},d^{*}})$는 체인 콤플렉스에 대한 이중 개념이다. ${\displaystyle {그것}_{}}$은 벡터 $공간$의 시퀀스로 ${\displaystyle {구성}_{}}$된다$.$ .${\displaystyle }$. . . . . . . . . . . . . . . . . . . . . . . . . .${\displaystyle }$.${\displaystyle }$. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .$$.$,C_{0},C_{1},C_{2},C_{3},C_{4},...$$}$ 선형$$ ${\displaystyle {연산자}^{}{}^{}}$ :${\displaystyle {}^{}{C}^{}}$ n →${\displaystyle {\mathrm{C}}^{}}$ ${\displaystyle {}^{}}$ +$$1 {\$displaystyle$d^{$n}:$${\displaystyle C^{}}$$^{n}\to C^{n+1}:$ $d{\displaystyle {}^{}}$ n +${\displaystyle {}^{}{}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle d^{}}$= ${\displaystyle 0}$ ${\displaystyle d^{n+1}\circle d^{n}=0}$. 코체인 콤플렉스는 체인 콤플렉스와 유사한 방식으로 작성될 수 있다.

${\displaystyle \cdots {\xrightarrow {d^{-1}}}C^{0}{\xrightarrow {d^{0}}}C^{1}{\xrightarrow {d^{1}}}C^{2}{\xrightarrow {d^{2}}}C^{3}{\xrightarrow {d^{3}}}C^{4}{\xrightarrow {d^{4}}}\cdots }$

$C{\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$ 또는$$ $C{\displaystyle {}^{}}$ ${\displaystyle n^{}}$ ${\$의 지수 $n{\displaystyle }$ ${\displaystyle n}$을(를) 도(또는 치수)라고 한다$$. 체인단지와 코체인단지의 차이는 체인단지의 경우 차원이 줄어드는 반면, 코체인단지의 경우 차원이 늘어난다는 점이다.

a(co)체인 콤플렉스의 개별 벡터 공간의 요소를 코체인이라고 한다. $d{\displaystyle }$ ${\displaystyle d}$의 커널에 있는 원소를 cocyles(또는 닫힌 원소)라고 하고$$, $d{\displaystyle }$ ${\displaystyle d}$의 영상에 있는 원소를 coboundary(또는 정확한 원소)라고$$ 한다. 미분 정의에서 바로, 모든 경계는 사이클이다.

The Poincaré lemma states that if ${\displaystyle B}$ is an open ball in ${\displaystyle {\bf {R}}^{n}}$, any closed ${\displaystyle p}$-form ${\displaystyle \omega }$ defined on ${\displaystyle B}$ is exact, for any integer ${\displaystyle p}$ with ${\displaystyle 1\leq p\leq$$n}$ $.$

$코칭$을 이산(차동) 형태라고 할 때 d ${\displaystyle$ d$}$을(를) 외부 파생 모델로 지칭한다. 우리는 또한 미적분 표기법을 형태들의 값에 사용한다.

$\displaystyle \omega(s)=\int_{s}\omega.}$

스톡스의 정리는 다지관의 이산 미분 형태에 관한 진술로, 구간의 분할에 대한 이산 미적분학의 기본 정리를 일반화한다.

${\displaystyle \sum _{i=0}^{n-1}{\frac {\Delta F}{\Delta x}}(a+ih+h/2)\\\\Delta x=F(b)-F(a).}$

스톡스의 정리에 따르면 일부 방향성 $매니폴드{\displaystyle \mathrm{}}$ Ω의 경계 위에 있는$$ 폼 Ω$${\$displaystyle \Oomega}$의 합은 $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle$ $d$$\Oomega},$즉, 전체 Ω에$$ 걸쳐 외부 파생상품 ${\displaystyle \mathrm{d\Omega }}$의 합계와 동일하다$$.

${\displaystyle \int _{\Oomega }d\omega =\int _{\partial \Oomega }\momega \,}$

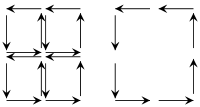
$d{\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle d=2}$차원에$$ 대한 예를 들어 기본 원리를 검토할 가치가 있다. 본질적인 아이디어는 다지관의 방향 타일링에서 내부 경로가 반대 방향으로 교차된다는 것을 보여주는 왼쪽의 도표로 이해할 수 있다. 즉, 내부 경로가 통합된 경로에 대한 기여는 서로 쌍방향으로 취소된다. 그 결과, 경계로부터의 공헌만 남는다.

참조를 참조하십시오.^{[11] [10]}

폼의 쐐기 제품

이산형 미적분학에서, 이것은 더 높은 순서의 형태로부터 만들어지는 구조로, $도{\displaystyle }$ p$[\displaystyle$ p$}$와 q$[\displaystyle q}$의 두 개의 동점을 연결하여 도 $p{\displaystyle }$ +$[\displaystyle p+q}$의 복합 코체인을 형성한다$.$

입체 복합체의 경우, 쐐기 제품은 동일한 차원의 벡터 공간으로 보이는 모든 입방체에서 정의된다.

단순화 콤플렉스의 경우 쐐기 제품을 컵 제품으로 구현한다: f ${\displaystyle p^{}}$ ${\$가 $p{\displaystyle }$ ${\displaystyle p}$ -cochain이고$$ ${\displaystyle g^{}}$ $Q{\displaystyle {}^{}}$ ${\$는 $q{\displaystyle }$ ${\displaysty q}$ -cochain인$$ 경우

${\displaystyle (f^{p}\p^ g^{q})(\f^{p})(\pma _{0,1,...,p}\cdot g^{q}(\p,p+1,...,p+q})$

where ${\displaystyle \sigma }$ is a ${\displaystyle (p+q)}$ -simplex and ${\displaystyle \sigma _{S},\ S\subset \{0,1,...,p+q\}}$, is the simplex spanned by ${\displaystyle S}$ into the ${\displaystyle (p+q)}$-simplex whose vertices are indexed by ${\displaystyle \{}$${\displaystyle \{0,...,p+q\}}$. So, ${\displaystyle \sigma _{0,1,...,p}}$ is the ${\displaystyle p}$-th front face and ${\displaystyle \sigma _{p,p+1,...,p+q}}$ is the ${\displaystyle q}$-th back face of ${\displaystyle \sigma }$, res속셈으로

코인 $f{\displaystyle {}^{}}$ ${\displaystyle p^{}}$ ${\$와 $g{\displaystyle {}^{}}$ ${\displaystyle q^{}}$ ${\$의 컵 제품의 공동 경계는 다음과$$ 같다.

${\displaystyle d(f^{p}\required g^{p}}}=d{f^{p}}\p^{p}+(-1)^{p}(f^{p}\p^d{g^{q}}).}$

두 개의 코코클의 컵 제품은 다시 코코클이며, (어느 순서로든) 코코클이 있는 코바운드리 제품은 코바인이다.

컵 제품 작동이 ID를 충족함

${\displaystyle \cHB \p}\reason \p}=(-1)^{pq}(\reason ^{q}\reason \reason \p}).}$

즉, 해당 곱셈은 등급 부여된다.

참조를 참조하십시오.^[11]

라플라스 연산자

꼭지점 $p{\displaystyle }$ ${\$$displaystyle p}$에 있는 $함수{\displaystyle }$ f$${\$displaystyle f$$\}$의 Laplace 연산자 ${\displaystyle \mathrm{\Delta f}}${\$delta$ f$}은(최대$) p {\$displaystyle$ p$}$의 셀룰러 $근방$에 대한 f {\$displaystystyle f}$의 평균 값이 f${\displaystyle }$($p)$에서 벗어나는$$ 비율이다$.$ 라플라스 연산자는 함수의 구배 흐름의 플럭스 밀도를 나타낸다. 예를 들어, 유체에 용해된 화학물질이 특정 지점에서 라플라스 연산자와 비례하는 순 속도는 그 지점의 화학농도의 라플라스 연산자에 비례한다. 상징적으로 표현하면 결과 방정식은 확산방정식이다. 이러한 이유로 다양한 물리적 현상을 모델링하는 데 과학에서 광범위하게 사용된다.

코디프렌더

${\displaystyle \delta :C^{k}\to C^{k-1}$

$k{\displaystyle }$ ${\displaystyle k}$ -displays에$$ 정의된 연산자:

${\displaystyle \cHB =(-1)^{n(-1)-1}+1}{\d{\d(-1)=(-1)^{k}\,{\star }^{-1d{\star }}}}}}$

여기서 $d{\displaystyle }$ ${\displaystyle d}$은(는) 외부 파생 모델 또는 디퍼렌셜이고${\displaystyle }$and$$ ${\displaystyle \star }$은(는) Hodge star 연산자다.

코디프유는 스톡스의 정리에 따른 외부 파생상품의 부선이다.

$(\displaystyle,\eta,\beat \zeta )=(d\eta,\zeta).}$

차등이 d ${\displaystyle {2\mathrm{}}^{}}$= ${\displaystyle 0}$ ${\displaystyle d^{2}=0}$을$($를) 만족하므로 코드프렌더에는 해당 속성이 있다.

$\d^{2}={\star }{\d{\d}d{\star }{\d}d{\d}d{\d(n-k)^{\d^{2}{\star }=0.}$

라플라스 연산자는 다음과 같이 정의된다.

${\displaystyle \Delta =(\delta +d)^{2}=\delta d+d\delta .}$

참조를 참조하십시오.^[10]

관련

• 이산요소법
• 구분차이
• 유한차계수
• 유한차법
• 유한요소법
• 유한 부피법
• 수치분화
• 수치적 통합
• 일반 미분방정식의 수치적 방법

참고 항목

• 유한차이의 미적분학
• 유한 가중 그래프에 대한 미적분
• 셀룰러 오토매틱
• 이산 미분 기하학
• 이산 라플라스 연산자
• 유한차이의 미적분, 이산 미적분 또는 이산해석
• 이산 모스 이론

참조