"융합(수학)"은 여기서 리디렉션된다. 다른 용도는 수렴(동음이의 )을 참조하십시오. 수학 에서, 시리즈 는 수의 무한 시퀀스 용어의 합 이다. 더 정확히 말하면, 무한 시퀀스(0 , a 1 2 {\displaystyle (a_{0},a_{1},a_{2},\ldots )} 시리즈 S 를 정의한다
S = a 0 + a 1 + a 2 + ⋯ = ∑ k = 0 ∞ a k . {\displaystyle S=a_{0}+a_{1}+a_{1}+a_{2}+\cdots =\sum _{k=0}^{\inful }a_{k}. } n번째부분 합계 S n 번째
S n = ∑ k = 1 n a k . {\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}. } A series is convergent (or converges ) if the sequence ( S 1 , S 2 , S 3 , … ) {\displaystyle (S_{1},S_{2},S_{3},\dots )} limit ; that means that, when adding one a k {\displaystyle a_{k}} in the order given by the indices , one gets partial sums that become closer and clo 일정한 수에 따르다 보다 정확히 말하면, 시리즈 {\displaystyle \ell} ε {\displaystyle \varepsilon }, 모든 ≥ N {\displaystyle \geq } 정수 N {\displaystyfully ) .
S n − ℓ < ε . \displaystyle \left S_{n}-\ell \right <\varepsilon .} 시리즈가 수렴된 경우 (필요적으로 고유한) 숫자 ℓ {\displaystyle \ell } 시리즈의 합 이라고 한다
같은 표기법
∑ k = 1 ∞ a k {\displaystyle \sum _{k=1}^{\inful }a_{k}}} 시리즈에 사용되며, 수렴할 경우 합계에 사용된다. 이 b a 와 b 더하는 연산 뿐만 아니라 이 덧셈 의 결과를 의미하는데, 이를 a 와 b 의 합 이라고 한다.
수렴하지 않는 모든 시리즈는 다이버전트 또는 다이버전트라고 한다.
수렴성 및 다이버전트 계열의 예 양의 정수 의 왕복은 다음과 같은 상이한 시리즈 (화합물 시리즈 )를 생성한다. 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ⋯ → ∞ . {\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \1 \over 5}+{1 \1 \over 6}+\cdots \rightarrow \infty .} 양의 정수의 왕복선 부호를 교대하면 수렴 연속(대체 고조파 직렬 )이 생성된다. 1 1 − 1 2 + 1 3 − 1 4 + 1 5 − ⋯ = ln ( 2 ) {\displaystyle {1 \over 1-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}-\cdots =\ln(2)} 소수 왕복선은 다양한 시리즈 를 생성한다(따라서 소수 집합은 "크다 "; 소수 왕복 합계의 차이 를 참조). 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + ⋯ → ∞ . {\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .} 삼각형 숫자 의 왕복선은 수렴 열을 생성한다. 1 1 + 1 3 + 1 6 + 1 10 + 1 15 + 1 21 + ⋯ = 2. {\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2. } 요인 왕복선은 수렴 열을 생성한다(e 참조): 1 1 + 1 1 + 1 2 + 1 6 + 1 24 + 1 120 + ⋯ = e . {\displaystyle {\frac {1}{1}:{1}:{1}{1}:{1}:{1}:{1}{1}:{1}{1}{1}:{\frac {{1}:{6}+{1}{1}:{\frac {1}:{120}+\cdots =e. } 제곱수 의 왕복은 수렴 열을 생성한다(바젤 문제 ). 1 1 + 1 4 + 1 9 + 1 16 + 1 25 + 1 36 + ⋯ = π 2 6 . {\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \1 \over 25}+{1 \1 \over 36}+\cdots ={\pi ^{2} \2} \}}}}} 2 의 힘의 왕복선은 수렴 시리즈를 생성한다(따라서 2의 세트 는 "작다" 1 1 + 1 2 + 1 4 + 1 8 + 1 16 + 1 32 + ⋯ = 2. {\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2} } n>1의 힘 의 왕복선은 다음과 같은 수렴 시리즈를 생성한다. 1 1 + 1 n + 1 n 2 + 1 n 3 + 1 n 4 + 1 n 5 + ⋯ = n n − 1 . {\displaystyle {\1 \over 1}+{1 \over n}+{1 \over n^{2}}+{1 \over n^{3}}+{1 \over n^{4}}}+{1 \over n^{5}}}}+\cdots ={n \n-1}. } 2의 힘 의 왕복 신호도 교대로 수렴 전열을 생성한다. 1 1 − 1 2 + 1 4 − 1 8 + 1 16 − 1 32 + ⋯ = 2 3 . {\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots = {2 \over 3}. } n>1의 힘의 왕복 신호를 교대하면 다음과 같은 수렴 시리즈가 생성된다. 1 1 − 1 n + 1 n 2 − 1 n 3 + 1 n 4 − 1 n 5 + ⋯ = n n + 1 . {\displaystyle {\1 \over n}-{1 \over n}+{1 \over n^{2}}-{1 \over n^{3}+{1 \over n^{5}}-{1 \over n+1}. 피보나치 숫자 의 왕복선은 수렴 전열을 생성한다(ψ : ):: 1 1 + 1 1 + 1 2 + 1 3 + 1 5 + 1 8 + ⋯ = ψ . {\displaystyle {\frac {1}{1}:{1}:{1}:{1}:{1}{1}:{1}:{1}:{1}:{1}:{1}:{2}}+{\frac {1}}{3}+{5}}{{5}}}}{\frac {1}{1}}}}}{8}}}+\frac {cdots =\cd.}}}}}}}}} 수렴시험 시리즈가 수렴 또는 분산되는지 를 결정하는 방법에는 여러 가지가 있다.
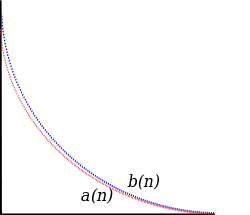
파란색 시리즈인 , b {\ displaystyle \Sigma b_{n} ( 시리즈 a {\ displaystyle \Sigma a_{n} 대조적으로, 빨간색 시리즈 series {{\ displaystyle \Sigma a_{n}} b displaystyle \Sigma b_{n} 비교 테스트 시퀀스 n {\ displaystyle \left\{a_{n}\right\}} b }{b_{n}\right\}} .
for all n , 0 ≤ a n ≤ b n {\displaystyle 0\leq \ a_{n}\leq \ b_{n}} ∑ n = 1 ∞ b n {\displaystyle \sum _{n=1}^{\infty }b_{n}} ∑ n = 1 ∞ a n . {\displaystyle \sum _{n=1}^{\infty }a_{n}. }
하지만, 만약,
for all n , 0 ≤ b n ≤ a n {\displaystyle 0\leq \ b_{n}\leq \ a_{n}} ∑ n = 1 ∞ b n {\displaystyle \sum _{n=1}^{\infty }b_{n}} ∑ n = 1 ∞ a n . {\displaystyle \sum _{n=1}^{\infty }a_{n}. }
비율 검정 모든 n 에 대해 n {\ displaystyle a_{n} 다음과 같은r {\displaystyle r}
임이 있는 n → ∞ a n + 1 a n = r . {\displaystyle \lim_{n\to \flt}\왼쪽 {\frac {a_{n+1}{a_{n}}\오른쪽 =r.} r < 1이면 시리즈는 절대적으로 수렴된다. r 1 이면 시리즈가 분기한다. r 1일 경우 비율검사는 결론에 이르지 못하며, 시리즈는 수렴하거나 이탈할 수 있다.
루트 테스트 n번째 루트 테스트 . 해당 시퀀스의 조건이 음수 가 아니라고 가정해 보십시오. r 을 다음과 같이 정의하십시오.
r = 임섭 n → ∞ a n n , {\displaystyle r=\limsup _{n\rightarrow \infit }{\sqrt[{n}]{a_{n}}},} 여기서 "lim supp"은 한계 상위 를 나타낸다(각각 ∞; 한도가 존재할 경우 동일한 값). r < 1일 경우, 영상 시리즈가 수렴한다. r 1 이면 시리즈가 분기한다. r 1일 경우 루트 테스트는 결론을 내리지 못하며, 시리즈가 수렴하거나 이탈할 수 있다.
비율 검정과 루트 테스트는 모두 기하 계열과의 비교를 기반으로 하며, 이와 같이 유사한 상황에서 작동한다. 실제로 비율검사가 효과가 있다면(한계가 존재하고 1과 같지 않다는 의미) 뿌리검사도 효과가 있다. 그러나 그 반대는 사실이 아니다. 따라서 루트 테스트는 보다 일반적으로 적용 가능하지만, 실제적인 문제로서 일반적으로 볼 수 있는 유형의 시리즈에 대한 한계는 계산하기가 어려운 경우가 많다.
적분 시험 이 시리즈는 수렴 또는 분열을 확립하기 위한 필수 요소와 비교할 수 있다. Let f n n {\ displaystyle f(n)=a_{n}} 감소하는 함수 다. 만약
∫ 1 ∞ f ( x ) d x = 임이 있는 t → ∞ ∫ 1 t f ( x ) d x < ∞ , {\displaystyle \int _{1}^{\inf(x)\,dx=\lim _{t\to \inft }\int _{1}^{t(x)\,dx<\inflt ,} 그러면 시리즈가 수렴된다. 하지만 만약 본질적인 것이 분산된다면, 그 시리즈도 그렇게 한다.
한계 테스트 만약{는 n},{bn}>0{\displaystyle \left\{a_{n}\right\},\left\{b_{n}\right\}>0}일 경우와 n→ ∞ nbn{\displaystyle \lim_{n\to\infty}{\frac{a_{n}}{b_{n}}lim}}지 않는다고 0, 그때 ∑ 존재하는 nx1과 만약에 ∞ 오빠{\displaystyle \sum_{n=1}^{\infty}a_{n}}전진.ly 만약 ∑ n 1 ∞ b {\ displaystyle \sum _{n=1}^{\inflt }b_{n}}}
교번 직렬 테스트 Also known as the Leibniz criterion , the alternating series test states that for an alternating series of the form ∑ n = 1 ∞ a n ( − 1 ) n {\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}} { a n } {\displaystyle \left\{a_{n}\right\}} decreasing , and has a limit of 0 at infinity, then the se 리즈가 응집되다
코치 응축 시험 If { a n } {\displaystyle \left\{a_{n}\right\}} ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} ∑ k = 1 ∞ 2 k a 2 k {\displaystyle \sum _{k=1}^{\infty }2^{k}a_{2^{k}}}
디리클레 테스트
아벨의 시험
조건부 및 절대 수렴 모든 시퀀스 a a 2 3 displaystyle \left\{a_{1},\ a_{2},\ {3},\dots \right\}}, n ≤ a {\ displaystystyle a_{n \reft riged a_n}\riged }\}}}}}} 그러므로
∑ n = 1 ∞ a n ≤ ∑ n = 1 ∞ a n . {\displaystyle \sum \sum \{n=1}{n}\leq \sum \sum _{n=1}^{n=1}\ft an_{n}\{n}\오른쪽 .} 즉, ∑n 1 ∞ n {\ displaystyle \sum \sum _{ n}\좌측 a_{n}\right nn 1 a displaystysty \sum _{n=1}^{\a_{n }}}}}}}}}}}}}
시리즈 ∑n 1 ∞ n {\ displaystyle \sum _{n=1}^{\infit }\왼쪽 a_{n}\right }} 수렴 되면 시리즈∑n 1 { n {\ displaystystyle \sum _{n=1}^{\inftra_n}}}}n}}}}}}}}}}}}}n 지수함수 의 Maclaurin 계열 은 변수의 모든 복잡한 값에 대해 절대적으로 수렴된다.
If the series ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }\left a_{n}\right } ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} conditionally convergent . logarithm 함수 ln 1 {\displaystyle \ln(1+x)} x 1 에 대해 조건상 수렴된다
리만 시리즈 정리 는 시리즈가 조건부로 수렴할 경우 시리즈가 어떤 가치로 수렴하거나, 혹은 심지어 분산되는 방식으로 시리즈 조건을 재배열할 수 있다고 기술하고 있다.
균일 수렴 { f 1 f f 3 {\ displaystyle \left\{f_{1},\ f_{2},\ f_{3},\dots \right\}}} 시리즈 ∑n 1 ∞ f displaystyle \sum {n=1}^{\nf_{n}}}} n }{\displaystyle s_{n}\}}}}
s n ( x ) = ∑ k = 1 n f k ( x ) {\displaystyle s_{n}(x)=\sum _{k=1}^{n}f_{k}(x)} 균일하게 f 에 수렴하다.
Weierstrass M-테스트라고 하는 무한 일련의 기능에 대한 비교 테스트의 아날로그가 있다.
코치 수렴 기준 Cauchy 수렴 기준 에서 시리즈는
∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\nft }a_{n}}} 부분 합계 의 순서가 Cauchy 시퀀스 인 경우 에만 수렴한다. 즉, 모든 ε 0 , {\displaystyle \varepsilon >0,} 모든 n ≥ m ≥ displaystyle n\ m\geq N} 정수 {\displaystystyle N}
∑ k = m n a k < ε , {\displaystyle \left \sum _{k=m}^{n}a_{k}\오른쪽 <\varepsilon ,} 에 해당하는
임이 있는 n → ∞ m → ∞ ∑ k = n n + m a k = 0. \displaystyle \lim _{n\to \up m\to \infit }\to \infit }\sum _{k=n}^{n+m}a_{k}=0. } 참고 항목 외부 링크





 (가) 존재하면 임의의 작은 모든 양수
(가) 존재하면 임의의 작은 모든 양수 


























![r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5eebb0f17b1155c0bea36edfdd50d6b9aa0f01)
 양수적이고 단조롭게
양수적이고 단조롭게 













 (가) 있음을 의미한다.
(가) 있음을 의미한다. 




