수학함수
삼각측량 사인 sin( πx /)( pale 점선 빨간색)과 비교하여 실제 인수에 적용되는 렘니세이트 사인(빨간색) 및 렘니세이트 코사인(purple). 수학 에서 렘니세이트 타원함수 는 베르누이의 렘니세이트 의 원호 길이와 관련된 타원함수 입니다.그것들은 1718년에 Giulio Fagnano 에 의해 처음 연구되었고, 다른 것들 중에서 Leonhard Euler 와 Carl Friedrich Gauss 에 의해 나중에 연구되었습니다.[1]
일반적으로 sl 및 cl 기호로 쓰여진 렘니세이트 사인 및 렘니세이트 코사인 함수는 삼각 함수 사인 및 코사인과 유사합니다(또는 sinlem 및 coslem 또는 sinlem 및 cosemn 이 대신 사용되기도 함).[2] 삼각 사인은 원호 길이를 단위 - diameter x 2 y , displaystyle ^{2} ,} x 2 y 2 2 y 2 displaystyle {\bigl x^{2 ^{2}{\bigr )}{}^{2 ^{2} ^{2}}.
렘니스케이트 함수에는 숫자 ϖ = {\displaystyle \varpi 2.622057 과 관련된 주기가 있습니다. 렘니스케이트 상수 라 불리는, 렘니스케이트의 둘레와 지름의 비율.이 숫자는 원의 지름에 대한 둘레의 비율 인 (quadratic) π = {\displaystyle \pi 3.141592... 의 4차 아날로그입니다.
복잡한 함수 로서, sl 과 cl 은 기본 주기 가 {( 1 i ) }, ( 1 i ) }, {\displaystyle \{(1+i)\varpi, (1-i)\varpi \}} 주기 격자 (가우시안 정수 의 배수)를 가지며, 해당 격자에 두 개의 야코비 타원 함수 인 sl sn z ; i ), {\displaystyle \operatorname {sl} operatornam e {sn}(z;i),} cl z = cd ( z ; i ) {\displaystyle \operatorname {cl = operatorname {cd}(z;i)}.
마찬가지로 쌍곡 렘니스케이트 사인 slh 및 쌍곡 렘니스케이트 코사인 clh 는 기본 주기가 2 , 2 } . {\displaystyle {\bigl \{}{\sqrt {2}}\varpi {\sqrt {2}}\varpi {\bigr \}}.
렘니스케이트 함수 및 쌍곡 렘니스케이트 함수는 Weiersstrass 타원 함수 ( z ; a , 0 ) {\displaystyle \wp(z;a,0)} 관련 이 있습니다.
렘니스케이트 사인 및 코사인 함수 정의들 렘니스케이트 함수 sl 과 cl 은 초기값 문제 의 해결책으로 정의할 수 있습니다.[5]
d d z 슬 z = ( 1 + 슬 2 z ) cl z , d d z cl z = − ( 1 + cl 2 z ) 슬 z , 슬 0 = 0 , cl 0 = 1 , {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}\operatorname {sl} z={\bigl (}1+\operatorname {sl}^{2}z{\bigr )}\operatorname {cl} z,\frac {\mathrm {d} {\mathrm {d} z}\operatorname {cl} z=-{\bigl (}1+\operatorname {cl}^{2}z{\bigr )}\operatorname {sl} 0=0,\operatorname {cl} 0=1,} 또는 타원 적분 의 역수로서 복소 단위 원판 에서 모서리 가 있는 정사각형 {12 , 12 ϖ i, 12 , 12 i } {\displaystyle {\big \{}{\tfrac {1}{2}}\varpi {\tfrac {1}{2}}\varpi {\tfrac {1}{2}}\varpi {\tfrac {1}{2}\varpi i{\big \}\colon }
z = ∫ 0 슬 z d t 1 − t 4 = ∫ cl z 1 d t 1 − t 4 . {\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}. 그 사각형 너머에서, 함수들은 일련의 반사 에 의해 복소 평면 전체 에 분석적으로 계속 될 수 있습니다.
이에 비해 원형 사인과 코사인은 초기 값 문제의 해결책으로 정의할 수 있습니다.
d d z 죄악의 z = cos z , d d z cos z = − 죄악의 z , 죄악의 0 = 0 , cos 0 = 1 , {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}\sin z=\cos z,\{\frac {\mathrm {d} z}\cos z=-\sin z,\ \sin 0=0,\cos 0=1,} 또는 위의 반평면 에서 실제 부분이 -12 , 12 {\displaystyle -{\tfrac {1}{2}}\pi, tfrac {1}{2}\pi},
z = ∫ 0 죄악의 z d t 1 − t 2 = ∫ cos z 1 d t 1 − t 2 . {\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}} 렘니세이트 상수와의 관계 렘니세이트 사인 함수와 쌍곡 렘니세이트 사인 함수는 타원 적분의 역으로 정의됩니다. 완전 적분은 렘니세이트 상수 ϖ과 관련이 있습니다. 렘니스케이트 함수는 최소 실수 주기 2 ϖ, 최소 허수 주기 2 ϖi 및 기본 복소 주기 (1 i ) {\displaystyle (1+i)\varpi } (1 i displaystyle (1-i)\varpi } 합니다
ϖ = 2 ∫ 0 1 d t 1 − t 4 = 2.62205 … {\displaystyle \varpi = 2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}=2.62205\ldots } 렘니스케이트 함수는 기본 관계 cl z sl (12 ), {\displaystyle \operatorname {cl} operatorname {sl}}{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )} . cos sin 12 z {\ displaystyle cos z sin }{\bigl (}{\tfrac {1}}\pi -z{\bigr )}.
렘니세이트 상수 상수 π의 가까운 유사체이며, 삼각함수 를 포함하는 동일체는 렘니세이트 함수를 포함하는 유사체를 가지므로 π을 포함하는 많은 동일체는 ϖ을 포함하는 유사체를 갖습니다. 예 비엣의 공식 은 다음과 같이 쓸 수 있습니다.
2 π = 1 2 ⋅ 1 2 + 1 2 1 2 ⋅ 1 2 + 1 2 1 2 + 1 2 1 2 ⋯ {\displaystyle {\frac {2}{\pi}}={\sqrt {\frac {1}{2}}\cdot {\sqrt {\frac {1}{2}}}\cdot {\sqrt {\frac {1}{2}}}\cdot {\sqrt {\frac {1}{2}}+{\frac {1}}{\sqrt {1}}+{\frac {2}}}\cdots }
ϖ에 대한 유사한 공식은 다음과 같습니다.
2 ϖ = 1 2 ⋅ 1 2 + 1 2 / 1 2 ⋅ 1 2 + 1 2 / 1 2 + 1 2 / 1 2 ⋯ {\displaystyle {\frac {2}{\varpi}}={\sqrt {\frac {1}{2}}\cdot {\sqrt {\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\! {\sqrt {\frac {1}{2}}}\cdot {\sqrt {\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\! {\sqrt {\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\! {\sqrt {\frac {1}{2}}}}}\cdots}
π의 기계 공식 은 14 π arctan 5 arctan 239 , textstyle {\tfrac {1}{ pi \arctan {\tfrac }{5}}-\arctan {\tfrac }{239 , arctan 2 arctan 3 {\textstyle }{4}\pi arctan {\ 1 rac {1}{2}}+\arctan {\tfrac {1}{3 다음 ϖ ϖ = 2 arcsl 1 2 arcsl 23 {\displaystyle {\tfrac {1}{2}}\varpi = 2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}. } [9]
렘니세이트와 원 상수는 가우스에 의해 산술-기하학 평균 M [10]
π ϖ = M ( 1 , 2 ) {\displaystyle {\frac {\pi}{\varpi}}=M{\left(1,{\sqrt {2}}\! ~\right) }}
인수 항등식 0, 극 및 대칭 sl {\displaystyle \operatorname {sl}} ( [11] 그림에서 기본 주기 1 i ) {\displaystyle (1 i)\varpi } 1 i {\displaystyle (1 )\varpi } 렘니세이트 함수 cl 과 sl 은 각각 짝수 및 홀수 함수 이고,
cl ( − z ) = cl z 슬 ( − z ) = − 슬 z {\displaystyle {\begin{aligned}\operatorname {cl}(-z)&=\operatorname {cl} z\[6mu]\operatorname {sl}(-z)&=-\operatorname {sl} z\end{aligned}} 12 {\displaystyle {\tfrac {1}{2}}\varpi ,} sl 을 교환하고, 12 displaystyle {\tfrac {1}{2}}i\varpi } 왕복 이동합니다.
cl ( z ± 1 2 ϖ ) = ∓ 슬 z , cl ( z ± 1 2 i ϖ ) = ∓ i 슬 z 슬 ( z ± 1 2 ϖ ) = ± cl z , 슬 ( z ± 1 2 i ϖ ) = ± i cl z {\displaystyle {\begin{aligned}{\operatorname {cl}}{\bigl(}z\pm {\tfrac {1}{2}}&=\mp \operatorname {sl} z,&{\operatorname {cl}}{\bigl(}z\pm {\tfrac {1}{2}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}\[6mu]{\operatorname {sl}}{\bigl(}z\pm {\tfrac {1}{2}}&=\pm \operatorname {cl} z, &{\operatorname {sl}}{\bigl(}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl}z}\end{aligned}} ϖ {\displaystyle varpi}( {\displaystyle \varpi ± {\displaystyle i\varpi}) 함수 가 무효화됩니다.
cl ( z + ϖ ) = cl ( z + i ϖ ) = − cl z 슬 ( z + ϖ ) = 슬 ( z + i ϖ ) = − 슬 z {\displaystyle {\begin{aligned}\operator name {cl}(z+\varpi)&=\operator name {cl}(z+i\varpi)=-\operator name {cl}(z+\varpi)&=\operator name {sl}(z+i\varpi)=-\operator name {sl} z\end{aligned}} 결과적으로, 두 함수 모두 ϖ {\displaystyle \varpi} 가우스-정수 곱셈에 의한 변환 하에서는 불변입니다. a b 대하여 + b k displaystyle 2k} a + bi ) , {\ ( a bi)\varpi,}
cl ( z + ( 1 + i ) ϖ ) = cl ( z + ( 1 − i ) ϖ ) = cl z 슬 ( z + ( 1 + i ) ϖ ) = 슬 ( z + ( 1 − i ) ϖ ) = 슬 z {\displaystyle {\begin{aligned}{\operatorname {cl}}{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl}{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl}z\[4mu]{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl}{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl}z\end{aligned}} 이것은 기본 주기 (1 i ) {\displaystyle (1 i)\varpi } 1 i {\displaystyle (1 )\varpi } 사각 주기 격자 를 갖는 타원 함수 (복소 평면에서 이중 주기 메로형 함수 )로 만듭니다. 사각형의 대칭을 따르고 있습니다.
렘니스케이트 함수 인수의 반사와 쿼터 턴 회전은 간단한 표현을 갖습니다.
cl z ¯ = cl z ¯ 슬 z ¯ = 슬 z ¯ cl i z = 1 cl z 슬 i z = i 슬 z {\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}\[6mu]\operatorname {sl}{\overline {\operatorname {sl} z}\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}} sl 함수는 ϖ 가우스 정수 배수에서 단순 0 , 정수 a b a b i {\displaystyle a\varpi +b\varpi i} 가우스 ϖ 반 정수 배수 의 단순 극 , 형태 a + 2 ( b 2 displaystyle bigl a tfrac {1}{2}}\varpi bigl {\tfrac { 1 }{2}}\bigr )}\varpi } 잔수 a b i {\displaystyle (-1)^{a 1}i . cl 함수는 sl 함수인 cl z sl 12 {\displaystyle \operatorname {cl} operatorname {sl}}{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr a + 1 + b i displaystyle bigl {\tfrac {1}{2}{\bigr )}\varpi \varpi } a b 1 ) i , {\displaystyle a\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi,} (- 1 ) . {\displaystyle (-1)^{a }i . }
또한.
슬 z = 슬 w ↔ z = ( − 1 ) m + n w + ( m + n i ) ϖ {\displaystyle \operatorname {sl} z=\operatorname {sl} w\왼쪽 오른쪽 화살표 z= (-1)^{m+n}w+(m+ni)\varpi } 일부 m, n Z {\displaystyle m,n\in \mathbb {Z}}
슬 ( ( 1 ± i ) z ) = ( 1 ± i ) 슬 z 슬 ′ z . {\displaystyle \operatorname {sl}((1\pm i)z)=(1\pm i){\frac {\operatorname {sl} z}{\operatorname {sl} 'z}}}} 마지막 공식은 복소수 곱셈 의 특수한 경우입니다. sl mi {\displaystyle \operator {sl} ((n+ mi)z) } n mi {\displaystyle n mi} sl displaystyle operatorname sl} ( Zi ] {\displaystyle \mathbb {Z}[i]} . [15]
sl 의 0과 극의 분포를 반영하는 무한급수도 있습니다.[16] [17]
1 슬 z = ∑ ( n , k ) ∈ Z 2 ( − 1 ) n + k z + n ϖ + k ϖ i {\displaystyle {\frac {1}{\operatorname {sl} z}}=\sum _{(n,k)\in \mathbb {Z}^{2}}{\frac {(-1)^{n+k}}{z+n\varpi +k\varpi i}} 슬 z = − i ∑ ( n , k ) ∈ Z 2 ( − 1 ) n + k z + ( n + 1 / 2 ) ϖ + ( k + 1 / 2 ) ϖ i . {\displaystyle \operatorname {sl} z=-i\sum _{(n,k)\in \mathbb {Z}^{2}}{\frac {(-1)^{n+k}}{z+(n+1/2)\varpi +(k+1/2)\varpi i}} 피타고라스적 정체성 a 의 다양 값에 대한 a 녹색으로 음의 a a 빨간색 a = ±1 , 검은색 렘니세이트 함수는 피타고라스 와 유사한 항등식을 만족합니다.
c l 2 z + s l 2 z + c l 2 z s l 2 z = 1 {\displaystyle \operator name {cl^{2}} z+\operator name {sl^{2}} z\,\operator name {sl^{2}} z=1} 결과적으로 매개 변수 방정식 (x , ( cl t , sl t {\displaystyle (x, operatorname {cl} t,\operatorname {sl} )} 4차 곡선 x 2 2 2 y 2 1. x^{2} ^{2} x^{2}y^{2} 1.
이 ID는 번갈아가며 다시 작성할 수 있습니다.[18]
( 1 + c l 2 z ) ( 1 + s l 2 z ) = 2 {\displaystyle {\bigl (}1+\operatorname {cl^{2}} z{\bigr )} {\bigl (}1+\operatorname {sl^{2}} z{\bigr )}=2} c l 2 z = 1 − s l 2 z 1 + s l 2 z , s l 2 z = 1 − c l 2 z 1 + c l 2 z {\displaystyle \operatorname {cl^{2}} z={\frac {1-\operatorname {sl^{2}} z}{1+\operatorname {sl^{2}} z},\quad \operatorname {sl^{2} z={\frac {1-\operatorname {cl^{2}} z}{1+\operatorname {cl^{2} z}} 접선-합 연산자를 ⊕ b tan arctan a arctan ), {\displaystyle a\oplus b\mathrel \tan(\arctan a+\arctan b)
c l 2 z ⊕ s l 2 z = 1. {\displaystyle \operatorname {cl^{2}} z\opplus \operatorname {sl^{2}} z=1.} 함수 cl ~{\ displaystyle {\tilde {\ cl}}} displaystyle {\ {\operatorname {sl}}}
( ∫ 0 x cl ~ t d t ) 2 + ( 1 − ∫ 0 x 슬 ~ t d t ) 2 = 1. {\displaystyle \left(\int _{0}^{x}}{\tilde {\operatorname {cl}}}\,t\,\mathrm {d} t\right)^{2}+\left(1-\int _{0}^{x}{\tilde {\operatorname {sl}}}\,t\,\mathrm {d} t\right)^{2}=1} 파생상품 및 통합 파생상품은 다음과 같습니다.
d d z cl z = c l ′ z = − ( 1 + c l 2 z ) 슬 z = − 2 슬 z 슬 2 z + 1 c l ′ 2 z = 1 − c l 4 z d d z 슬 z = s l ′ z = ( 1 + s l 2 z ) cl z = 2 cl z cl 2 z + 1 s l ′ 2 z = 1 − s l 4 z {\displaystyle {\begin{aligned}{\frac {\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-{\bigl(}1+\operatorname {cl^{2}} z{\bigr}}\operatorname {sl} z=-{\frac {2\operatorname {sl} ^{2} z+1}\\\operatorname {cl'^{2} z&=1-\operatorname {cl^{4} z\[5mu]{\frac {\mathrm {d} z&\mathrm {d} z}\operatorname {sl} z}}-{\frac {2} z+1}\\operatorname {cl'^{2} z\[5mu]{\frac {\mathrm {d} z}}\operatorname {sl} {sl} z=\operatorname {sl'} z&={\bigl(}1+\operatorname {sl^{2}} z{\bigr}}\operatorname {cl} z={\frac {2\operatorname {cl} ^{2}z+1}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4} z\end{align} d d z cl ~ z = − 슬 ~ z cl z − 2 슬 z cl ~ 3 z cl 3 z d d z 슬 ~ z = 2 cl ~ z cl z − cl ~ z cl z {\displaystyle {\begin{aligned}{\frac {\mathrm {d}}{\mathrm {d} z}\,{\tilde {\operatorname {cl}}}\,z&=-\,{\tilde {\operatorname {sl}}\,z\operatorname {cl} z-{\frac {2\operatorname {sl} z\,{\tilde {\operatorname {cl}}^{3}z}\{\frac {\mathrm {d} z}\,{\tilde {\operatorname {sl}}\,z&=2\,{\tilde {\tilde {\peratorname {sl}}\,{\tilde {\tilde {\tilde {\til} z}},\frac {cl}^{3}z},\frac {\mathrm {d} z},\tilde {\mathrm {d} z}},\tilde {\operatorname {sl}},\,z&=2\,{\tilde {\tilde {\tilde {\til} torname {cl}}\,z\,\operatorname {cl} z-{\frac {\tilde {\operatorname {cl}}\,z}{\operatorname {cl} z}\end{aligned}} 렘니세이트 사인과 렘니세이트 코사인의 두 번째 유도체는 음의 중복 큐브입니다.
d 2 d z 2 cl z = − 2 c l 3 z {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}\operator name {cl} z=-2\operator name {cl^{3} z} d 2 d z 2 슬 z = − 2 s l 3 z {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}\operator name {sl} z=-2\operator name {sl^{3} z} 렘니세이트 함수는 역접합 함수를 사용하여 통합할 수 있습니다.
∫ cl z d z = 아크탄 슬 z + C ∫ 슬 z d z = − 아크탄 cl z + C ∫ cl ~ z d z = 슬 z cl ~ z cl z + C ∫ 슬 ~ z d z = − cl ~ z cl z + C {\displaystyle {\begin{aligned}\int \operatorname {cl} z\mathrm {d} z} &=\arctan \operatorname {sl} z+C\\int \operatorname {sl} z\mathrm {d} z+C\\int \operatorname {cl}\tilde {\operatorname {cl}}\,z\,\mathrm {d} z={\frac {\operatorname {sl} z\,{\tilde {\operatorname {cl}}\,z}{\operatorname {cl}}\,z}{\operatorname {cl}}+C\\\int {\t} \tilde {\operatorname {sl}}}\,z\,\mathrm {d} z&=-{\frac {\tilde {\operatorname {cl}}\,z}{\operatorname {cl} z}+C\end{aligned}} 인수합계 및 다중아이덴티티 삼각 함수와 마찬가지로 렘니세이트 함수도 인수 합과 차 항등식을 만족합니다. 파냐노가 렘니케이트를 이등분하기 위해 사용한 최초의 신원은 다음과 같습니다.[19]
슬 ( u + v ) = 슬 u s l ′ v + 슬 v s l ′ u 1 + s l 2 u s l 2 v {\displaystyle \operatorname {sl}(u+v)={\frac {\operatorname {sl} u\,\operatorname {sl'} v+\operatorname {sl} v\,\operatorname {sl'} u}{1+\operatorname {sl^{2} u\,\operatorname {sl^{2} v} 도함수와 피타고라스와 유사한 항등식은 파가노가 sl 과 cl 에서 사용한 항등식을 재작업하는 데 사용될 수 있습니다. 접선-합 연산자 b tan arctan a arctan {\displaystyle a\oplus b\mathrel \tan(\arctan a+\arctan )} a b a b ), {\displaystyle a\ominus \mathrel a\oplus (-b)
cl ( u + v ) = cl u cl v ⊖ 슬 u 슬 v = cl u cl v − 슬 u 슬 v 1 + 슬 u cl u 슬 v cl v cl ( u − v ) = cl u cl v ⊕ 슬 u 슬 v 슬 ( u + v ) = 슬 u cl v ⊕ cl u 슬 v = 슬 u cl v + cl u 슬 v 1 − 슬 u cl u 슬 v cl v 슬 ( u − v ) = 슬 u cl v ⊖ cl u 슬 v {\displaystyle {\begin{aligned}\operatorname {cl}(u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\,\operatorname {sl} v{1+\operatorname {sl} u\,\operatorname {cl} v\,\operatorname {cl} v}\[2mu]\operatorname {cl] rname {cl}(u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} v\[2mu]\operatorname {sl}(u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v},\operatorname {cl} v}\[2mu]\operatorname {sl}(u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}} 이들은 삼각형 유사체 와 유사합니다.
cos ( u ± v ) = cos u cos v ∓ 죄악의 u 죄악의 v 죄악의 ( u ± v ) = 죄악의 u cos v ± cos u 죄악의 v {\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\[6mu]\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}} 특히 실수 성분의 복소수 함수를 계산하기 위해서는
cl ( x + i y ) = cl x − i 슬 x 슬 y cl y cl y + i 슬 x cl x 슬 y = cl x cl y ( 1 − 슬 2 x 슬 2 y ) cl 2 y + 슬 2 x cl 2 x 슬 2 y − i 슬 x 슬 y ( cl 2 x + cl 2 y ) cl 2 y + 슬 2 x cl 2 x 슬 2 y 슬 ( x + i y ) = 슬 x + i cl x 슬 y cl y cl y − i 슬 x cl x 슬 y = 슬 x cl y ( 1 − cl 2 x 슬 2 y ) cl 2 y + 슬 2 x cl 2 x 슬 2 y + i cl x 슬 y ( 슬 2 x + cl 2 y ) cl 2 y + 슬 2 x cl 2 x 슬 2 y {\displaystyle {\begin{aligned}\operator name {cl}(x+iy)& ={\frac {\operatorname {cl} x-i\operatorname {sl} x\,\operatorname {sl} y\,\operatorname {cl} y} {\operatorname {cl} y+i\operatorname {sl} x\,\operatorname {sl} y}\[4mu]&={\frac {\operatorname {cl} x\,\operatorname {cl} y\left(1-\operatorname {sl}^{2}x\,\operatorname {sl}^{2}y\right)}{\operatorname {cl}^{2}y+\operatorname} {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}-i{\frac {\operatorname {sl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2}x+\operatorname {cl} ^{2}y\right)} {\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y}\[12mu]\operatorname {sl}(x+iy)& ={\frac {\operatorname {sl} x+i\operatorname {cl} x\,\operatorname {sl} y\,\operatorname {cl} y} {\operatorname {cl} y\,\operatorname {cl} x\,\operatorname {sl} y}\[4mu]&={\frac {\operatorname {sl} x\,\operatorname {cl} y\left(1-\operatorname {cl}^{2}x\,\operatorname {sl}^{2}y\right)}{\operatorname {cl}^{2}y+\operatorname} {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}+i{\frac {\operatorname {cl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y}\end{aligned}} 이등분선 공식:
cl 2 1 2 x = 1 + cl x 1 + 슬 2 x 1 + 슬 2 x + 1 {\displaystyle \operatorname {cl} ^{2}{\tfrac {1}{2}}x={\frac {1+\operatorname {cl}x{\sqrt {1+\operatorname {sl}^{2}x}}{{\sqrt {1+\operatorname {sl}^{2}x}}}}}} 슬 2 1 2 x = 1 − cl x 1 + 슬 2 x 1 + 슬 2 x + 1 {\displaystyle \operatorname {sl} ^{2}{\tfrac {1}{2}}x={\frac {1-\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}{{\sqrt {1+\operatorname {sl} ^{2}x}}}}} 복제 수식:[21]
cl 2 x = − 1 + 2 cl 2 x + cl 4 x 1 + 2 cl 2 x − cl 4 x {\displaystyle \operatorname {cl} 2x={\frac {-1+2\,\operatorname {cl}^{2}x+\operatorname {cl}^{4}x}{1+2\,\operatorname {cl}^{2}x-\operatorname {cl}^{4}x}} 슬 2 x = 2 슬 x cl x 1 + 슬 2 x 1 + 슬 4 x {\displaystyle \operatorname {sl} 2x=2\,\operatorname {sl} x\,\operatorname {cl} x{\frac {1+\operatorname {sl} ^{2}x} {1+\operatorname {sl} ^{4}x}} 곱셈 공식:[21]
cl 3 x = − 3 cl x + 6 cl 5 x + cl 9 x 1 + 6 cl 4 x − 3 cl 8 x {\displaystyle \operatorname {cl} 3x={\frac {-3\,\operatorname {cl} x+6\,\operatorname {cl}^{5}x+\operatorname {cl}^{9}x{1+6\,\operatorname {cl}^{4}x-3\,\operatorname {cl}^{8}x}} 슬 3 x = 3 슬 x − 6 슬 5 x − 1 슬 9 x 1 + 6 슬 4 x − 3 슬 8 x {\displaystyle \operatorname {sl} 3x={\frac {\color {red}{3}\,\color {black}{\operatorname {sl} x-\,}\color {green}{6}\,\color {black}{\operatorname {sl}^{5}x-\,}\color {blue}{1}\,\color {black}{sl}^{9}x}{\color {blue}{1}\,\color {black}{+\,}\color {green}{6}\,\color {black}{sl}^{4}x-\,}\color {red}{3}, \color {black}{\operator name {sl}^{8}x}}} sl x {\displaystyle \operatorname {sl} 3x} . 이 현상은 sl β x {\displaystyle \operatorname {sl} x} , β n {\displaystyle m+ni}, n Z {\displaystyle m, n\in \mathbb {Z}} n {\displaystyle m+n}
렘원자 다항식 L 격자 라고 하자 L}
L = Z ( 1 + i ) ϖ + Z ( 1 − i ) ϖ . {\displaystyle L=\mathbb {Z}(1+i)\varpi +\mathbb {Z}(1-i)\varpi.} 또한 K Q i {\displaystyle mathbb {Q} (i O i {\displaystyle {\mathcal {O mathbb {Z} [i z C {\displaystyle z\in \mathbb {C {\displaystyle \m+in} β m +, {\displaystyle \m + in} ' + in displaystyle m,n,m',n'\in \mathbb {Z}), m n displaystyle }), e m+n} m = n' {\displaystyle m'+n'} γ ≡ mod 2 ( 1 i ) {\displaystyle \equiv \,\operatorname {mod} \,2(1+i)} sl β z = M β sl ) {\displaystyle \operatorname {sl beta = M_{\beta }(\operatorname {sl} )}. 그리고나서
M β ( x ) = i ε x P β ( x 4 ) Q β ( x 4 ) {\displaystyle M_{\beta}(x)=i^{\varepsilon}x{\frac {P_{\beta}(x^{4})}{Q_{\beta}(x^{4}}}} 일부 공임 다항식 P β x ), Q β O x {\displaystyle P_{\beta }(x), Q_{\beta }(x)\in {\mathcal {O}[x]} ε ∈ { 0 , 1 , 2 , 3 } {\displaystyle \varepsilon \in \{0, 1, 2, \},
x P β ( x 4 ) = ∏ γ β Λ γ ( x ) {\displaystyle xP_{\beta}(x^{4})=\prod _{\gamma \beta }\Lambda _{\gamma }(x)} 그리고.
Λ β ( x ) = ∏ [ α ] ∈ ( O / β O ) × ( x − 슬 α δ β ) {\displaystyle \Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O})^{\times}}}(x-\operatorname {sl} \alpha \delta_{\beta })} 여기서 δ β {\displaystyle \ _{\ β {\displaystyle δ β ∈ 1 β) L {\displaystyle \delta {\beta }\in (1/\ beta )L } δ β] ∈ 1 β) L {\displaystyle [\delta _{\beta }]\in (1 /\beta )L/L} ( ) O {\displaystyle {\mathcal {O}} 모듈 로 생성합니다. β {\displaystyle beta } 2개 β displaystyle 2\varpi beta 1 + ) β displaystyle +i)\varpi beta . ( ) O x {\ displaystyle Lambda {\beta x)\{\mathcal {O}[x]} displaystyle beta lemanomic 다항식 이라고 합니다.그것은 단성이고 K {\displaystyle K} . 사이클로토믹 다항식 의 "렘니케이트 유사체"입니다.[23]
Φ k ( x ) = ∏ [ a ] ∈ ( Z / k Z ) × ( x − ζ k a ) . {\displaystyle \Phi _{k}(x)=\prod _{[a]\in (\mathbb {Z} /k\mathbb {Z} )^{\times}}}(x-\zeta _{k}^{a}).} β {\displaystyle β ) {\displaystyle Lambda {\ x)} sl β {\ displaystyle \operatorname {sl} \ _ {\ } K[x] 최소 다항식 입니다. β sl ( β {\displaystyle \omega {\ operatorname {sl} (2\varpi /\ β ~ = s l 1 i ) ϖ β{\displaystyle {\omega}}_ {\bet operator {sl} ((1 i varpi /\be ta )}. K ω 5 displaystyle \omega {5}( 및 5의 {\tilde {\omega}}_{5 {\displaystyle K[x]} .
Λ 5 ( x ) = x 16 + 52 x 12 − 26 x 8 − 12 x 4 + 1 , {\displaystyle \Lambda _{5}(x)=x^{16}+52x^{12}-26x^{8}-12x^{4}+1,} 그리고[24]
ω 5 = − 13 + 6 5 + 2 85 − 38 5 4 {\displaystyle \omega_{5}={\sqrt[{4}}{-13+6{\sqrt{5}}+2{\sqrt{85-38{\sqrt{5}}}}}} ω ~ 5 = − 13 − 6 5 + 2 85 + 38 5 4 {\displaystyle {\tilde {\omega}}_{5}={\sqrt[{4}}{-13-6{\sqrt {5}}+2{\sqrt {85+38{\sqrt {5}}}}} [25] (동등식은 아래 표에 나와 있습니다.) 또 다른 예는[23]
Λ − 1 + 2 i ( x ) = x 4 − 1 + 2 i {\displaystyle \Lambda _{-1+2i}(x)=x^{4}-1+2i} ω - 1 2 {\ displaystyle omega _{-1+2i}}( 2 i {\displaystyle tilde omega {-1+2i}) x].
p {\displaystyle p} β beta} [27] [26]
도의 Λ β = β 2 ∏ p β ( 1 − 1 p ) ( 1 − ( − 1 ) ( p − 1 ) / 2 p ) {\displaystyle \operatorname {deg} \Lambda _{\beta }=\beta ^{2}\prod_{p \beta }\left(1-{\frac {1}{p}}\right)\left(1-{\frac {(-1)^{(p-1)/2}}{p}\right)} 사이클로토믹 유사체와 비교될 수 있는
도의 Φ k = k ∏ p k ( 1 − 1 p ) . {\displaystyle \operatorname {deg} \Phi _{k}=k\prod _{pk}\left(1-{\frac {1}{p}}\right).} 특정값 삼각함수와 마찬가지로 렘니세이트 함수의 값은 기본 산술과 제곱근만을 사용하여 렘니세이트를 같은 길이의 n개 n n 2k p 1 2 pm {\displaystyle 2^{k}p_{1}p_{2}\cdots p_{m} k 정수 이고 각 p 페르마 소수 입니다.
n {\displaystyle n} cl n ϖ {\displaystyle \operator name {cl} n\varpi } 슬 n ϖ {\displaystyle \operatorname {sl} n\varpi} 1 {\displaystyle 1} − 1 {\displaystyle -1} 0 {\displaystyle 0} 5 6 {\displaystyle {\tfrac {5}{6}} − 2 3 − 3 4 {\displaystyle -{\sqrt[{4}]{2{\sqrt {3}}-3}} 1 2 ( 3 + 1 − 12 4 ) {\displaystyle {\tfrac {1}{2}}{\bigl(}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}} 3 4 {\displaystyle {\tfrac {3}{4}} − 2 − 1 {\displaystyle -{\sqrt {\sqrt {2}}-1}} 2 − 1 {\displaystyle {\sqrt {\sqrt {2}}-1}} 2 3 {\displaystyle {\tfrac {2}{3}} − 1 2 ( 3 + 1 − 12 4 ) {\displaystyle -{\tfrac {1}{2}}{\bigl(}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}} 2 3 − 3 4 {\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}} 1 2 {\displaystyle {\tfrac {1}{2}}} 0 {\displaystyle 0} 1 {\displaystyle 1} 1 3 {\displaystyle {\tfrac {1}{3}} 1 2 ( 3 + 1 − 12 4 ) {\displaystyle {\tfrac {1}{2}}{\bigl(}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}} 2 3 − 3 4 {\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}} 1 4 {\displaystyle {\tfrac {1}{4}} 2 − 1 {\displaystyle {\sqrt {\sqrt {2}}-1}} 2 − 1 {\displaystyle {\sqrt {\sqrt {2}}-1}} 1 6 {\displaystyle {\tfrac {1}{6}} 2 3 − 3 4 {\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}} 1 2 ( 3 + 1 − 12 4 ) {\displaystyle {\tfrac {1}{2}}{\bigl(}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
추가값 n {\displaystyle n} cl n ϖ {\displaystyle \operator name {cl} n\varpi } 슬 n ϖ {\displaystyle \operatorname {sl} n\varpi} 3 7 {\displaystyle {\tfrac {3}{7}} 탄 { 1 2 아치형의 [ 1 2 2 cos ( 3 14 π ) 간이 침대 ( 1 28 π ) + cos ( 1 7 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth}{\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos ({\tfrac {3}{14}\pi )\cot ({\tfrac {1}{28}\pi )}+\cos ({\tfrac {1}{7}\pi ){\bigr \}}} 5 12 {\displaystyle {\tfrac {5}{12}} 1 2 8 4 [ 죄악의 ( 5 24 π ) − 3 4 죄악의 ( 1 24 π ) ] ( 2 3 + 3 4 − 1 ) {\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left ({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}\sin \left ({\tfrac {1}{24}\pi \right)\right]{ \Bigl(}{\sqrt[{4}]{2{\sqrt{3}}+3}}-1{\Bigr}} 1 2 8 4 [ 죄악의 ( 5 24 π ) − 3 4 죄악의 ( 1 24 π ) ] ( 2 3 + 3 4 + 1 ) {\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left ({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}\sin \left ({\tfrac {1}{24}\pi \right)\right]{ \Bigl(}{\sqrt[{4}}{2{\sqrt{3}}+3}}+1{\Bigr}} 2 5 {\displaystyle {\tfrac {2}{5}} 1 2 ( 5 4 − 1 ) ( 5 + 2 − 1 ) {\displaystyle {\tfrac {1}{2}}({\sqrt[4}}{5}}-1){\bigl(}{\sqrt{5}}+2}}-1{\bigr )} 2 5 − 2 4 죄악의 ( 3 20 π ) cos ( 1 20 π ) {\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}-2}}\,{\sqrt {\sin ({\tfrac {3}{20}}\pi )\cos ({\tfrac {1}{20}\pi )} 3 8 {\displaystyle {\tfrac {3}{8}} ( 2 4 − 1 ) ( 2 + 1 − 2 + 2 ) {\displaystyle {\sqrt {{4}}{\sqrt {2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}{\bigr )}}}. ( 2 4 − 1 ) ( 2 + 1 + 2 + 2 ) {\displaystyle {\sqrt {{4}}{\sqrt[{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}{\bigr )}}}. 5 14 {\displaystyle {\tfrac {5}{14}} 탄 { 1 2 아치형의 [ 1 2 2 죄악의 ( 1 7 π ) 간이 침대 ( 3 28 π ) + 죄악의 ( 1 14 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin ({\tfrac {1}{7}\pi )\cot ({\tfrac {3}{28}\pi )}+\sin ({\tfrac {1}{14}\pi ){\bigr \}\pi ){\bigr \}} 3 10 {\displaystyle {\tfrac {3}{10}} 2 5 − 2 4 죄악의 ( 1 20 π ) cos ( 3 20 π ) {\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}-2}}\,{\sqrt {\sin ({\tfrac {1}{20}}\pi )\cos ({\tfrac {3}{20}\pi )} 1 2 ( 5 4 − 1 ) ( 5 + 2 + 1 ) {\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}}{5}}-1{\bigr )}{\bigl (}{\sqrt{5}}+2}}+1{\bigr )}} 2 7 {\displaystyle {\tfrac {2}{7}} 탄 { 1 2 아치형의 [ 1 2 2 cos ( 1 14 π ) 태닝한 ( 5 28 π ) + 죄악의 ( 3 14 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth}{\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos ({\tfrac {1}{14}\pi )}\tfrac {5}\pi )}+\sin ({\tfrac {3}{14}\pi ){\bigr \}\pi ){\bigr \}} 3 14 {\displaystyle {\tfrac {3}{14}} 탄 { 1 2 아치형의 [ 1 2 2 cos ( 1 14 π ) 태닝한 ( 5 28 π ) + 죄악의 ( 3 14 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth}{\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos ({\tfrac {1}{14}\pi )}\tfrac {5}\pi )}+\sin ({\tfrac {3}{14}\pi ){\bigr \}\pi ){\bigr \}} 1 5 {\displaystyle {\tfrac {1}{5}} 1 2 ( 5 4 − 1 ) ( 5 + 2 + 1 ) {\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}}{5}}-1{\bigr )}{\bigl (}{\sqrt{5}}+2}}+1{\bigr )}} 2 5 − 2 4 죄악의 ( 1 20 π ) cos ( 3 20 π ) {\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}-2}}\,{\sqrt {\sin ({\tfrac {1}{20}}\pi )\cos ({\tfrac {3}{20}\pi )} 1 7 {\displaystyle {\tfrac {1}{7}} 탄 { 1 2 아치형의 [ 1 2 2 죄악의 ( 1 7 π ) 간이 침대 ( 3 28 π ) + 죄악의 ( 1 14 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin ({\tfrac {1}{7}\pi )\cot ({\tfrac {3}{28}\pi )}+\sin ({\tfrac {1}{14}\pi ){\bigr \}\pi ){\bigr \}} 1 8 {\displaystyle {\tfrac {1}{8}} ( 2 4 − 1 ) ( 2 + 1 + 2 + 2 ) {\displaystyle {\sqrt {{4}}{\sqrt[{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}{\bigr )}}}. ( 2 4 − 1 ) ( 2 + 1 − 2 + 2 ) {\displaystyle {\sqrt {{4}}{\sqrt {2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}{\bigr )}}}. 1 10 {\displaystyle {\tfrac {1}{10}} 2 5 − 2 4 죄악의 ( 3 20 π ) cos ( 1 20 π ) {\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}-2}}\,{\sqrt {\sin ({\tfrac {3}{20}}\pi )\cos ({\tfrac {1}{20}\pi )} 1 2 ( 5 4 − 1 ) ( 5 + 2 − 1 ) {\displaystyle {\tfrac {1}{2}}({\sqrt[4}}{5}}-1){\bigl(}{\sqrt{5}}+2}}-1{\bigr )} 1 12 {\displaystyle {\tfrac {1}{12}} 1 2 8 4 [ 죄악의 ( 5 24 π ) − 3 4 죄악의 ( 1 24 π ) ] ( 2 3 + 3 4 + 1 ) {\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left ({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}\sin \left ({\tfrac {1}{24}\pi \right)\right]{ \Bigl(}{\sqrt[{4}}{2{\sqrt{3}}+3}}+1{\Bigr}} 1 2 8 4 [ 죄악의 ( 5 24 π ) − 3 4 죄악의 ( 1 24 π ) ] ( 2 3 + 3 4 − 1 ) {\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left ({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}\sin \left ({\tfrac {1}{24}\pi \right)\right]{ \Bigl(}{\sqrt[{4}]{2{\sqrt{3}}+3}}-1{\Bigr}} 1 14 {\displaystyle {\tfrac {1}{14}} 탄 { 1 2 아치형의 [ 1 2 2 cos ( 3 14 π ) 간이 침대 ( 1 28 π ) + cos ( 1 7 π ) ] } {\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operator name {arcoth}{\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos ({\tfrac {3}{14}\pi )\cot ({\tfrac {1}{28}\pi )}+\cos ({\tfrac {1}{7}\pi ){\bigr \}}}
기하학적 도형과의 관계 베르누이 렘니케이트의 호 길이 렘니스케이트 사인과 코사인은 렘니스케이트의 원호 길이와 원점에서 한 끝점의 거리를 연관시킵니다. 삼각 사인과 코사인은 단위 지름 원의 원호 길이와 원점에서 한 끝점의 거리를 유사하게 연관시킵니다. 반치폭 1인 베르누이의 렘니스케이트 는 두 초점 F 1 1 2 , {\displaystyle F_{1 bigl (}{-{\tfrac {1}{\sqrt {2}}}, {\bigr )}, F 2 1 2 ,0 {\displaystyle F_{2 bigl (}{\tfrac {1}{\sqrt {2}}, 0{\bigr )}} 2 {\di spaystyle {\tfrac }{2}}. 극 방정식 r 2 = cos 2 θ {\displaystyle r^{2 = cos 2\theta} 데카르트 방정식 x 2 y 2 = x 2 y 2 . {\displaystyle {\bigl (}x^{2} y^{2}{\bigr )}{}^{2 = x^{2}-y^{2}} 사중 곡선 입니다.}
원점에서 거리 r {\displaystyle r} x 2 2 {\displaystyle x^{2} ^{2 }= r ^{2}} 하이퍼볼록스 y 2 = 4 {\displaystyle ^{2}-y^{2} = ^{4 정사분면의 교차점은 직교좌표를 갖습니다.
( x ( r ) , y ( r ) ) = ( 1 2 r 2 ( 1 + r 2 ) , 1 2 r 2 ( 1 − r 2 ) ) . {\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}\! {\sqrt{\tfrac {1}{2}}r^{2}{\bigr}}},\,{\sqrt{\tfrac {1}{2}r^{2}{\bigr}},\,{\bigr}},{\bigr}}. 렘니스케이트의 1/4에 대해 r [ 0 , 1 ] {\displaystyle r\in [0,1]} x ( r y r ) {\displaystyle {\big (}x(r),y(r ){\big )} 매개 변수화 를 사용하면 다음과 같습니다.
∫ 0 r x ′ ( t ) 2 + y ′ ( t ) 2 d t = ∫ 0 r ( 1 + 2 t 2 ) 2 2 ( 1 + t 2 ) + ( 1 − 2 t 2 ) 2 2 ( 1 − t 2 ) d t = ∫ 0 r d t 1 − t 4 = 호를 r . {\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t}\\&\quad {}=\int _{0}^{r}{\sqrt {(1+2t^{2})^{2}}}+{\frac {(1-2t^{2})^{2}}}{{2(1-t^{2}}}}\mathop {\mathrm {d} t}\[6mu]&\int {0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\[6mu]&\quad {}=\operatorname {arcsl} r. \end{aligned}} 마찬가지로, 1 , 0 ) {\displaystyle (1,0)} x r ), r {\ displaystyle {\big (}x(r),y(r){\big )}
∫ r 1 x ′ ( t ) 2 + y ′ ( t ) 2 d t = ∫ r 1 d t 1 − t 4 = 아크클 r = 1 2 ϖ − 호를 r . {\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t}\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}\varpi -\operatorname {arcsl} r.\end{aligned}} 또는 역방향에서 렘니세이트 사인 함수와 코사인 함수는 1 , 0 ) displaystyle (1,0)}
마찬가지로, 원형 사인 및 코사인 함수는 위의 동일한 인수를 사용하지만 매개 변수화를 사용하여 극성 방정식 r cos {\displaystyle cos \theta} x 2 y 2 x {\displaystyle x^{2} y^{2 x,}
( x ( r ) , y ( r ) ) = ( r 2 , r 2 ( 1 − r 2 ) ) . {\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}r^{2}},\,{\sqrt {r^{2}{\bigl (}1-r^{2}{\bigr )}\,{\biggr )}}. 또는, 단위 원 2 y 1 displaystyle ^{2} y^{2 1} (1 , 0 ) displaystyle(1, 0)} displaystyle s}
( x ( s ) , y ( s ) ) = ( cos s , 죄악의 s ) , {\displaystyle (x(s),y(s)=(\cos,\sin),} 렘니스케이트는 점 1 , 0 ) {\displaystyle(1,0)} 길이 {\displaystyles} [30]
( x ( s ) , y ( s ) ) = ( cl s 1 + 슬 2 s , 슬 s cl s 1 + 슬 2 s ) = ( cl ~ s , 슬 ~ s ) . {\displaystyle(x(s))=\left ({\frac {\operatorname {cl} s}{\sqrt {1+\operatorname {sl}^{2}s}},{\frac {\operatorname {sl} s\operatorname {cl} s}{\sqrt {1+\operatorname {sl}^{2}s}\right)=\left ({\tilde {\operatorname {cl}}\,s,{\tilde {\operatorname {sl}}\,s\right}. 렘니세이트 적분과 렘니세이트 함수는 1718년 파냐노가 발견한 중복 항등식을 만족합니다.[31]
∫ 0 z d t 1 − t 4 = 2 ∫ 0 u d t 1 − t 4 , 한다면 z = 2 u 1 − u 4 1 + u 4 그리고. 0 ≤ u ≤ 2 − 1 . {\displaystyle \int _{0}^{z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}=2\int _{0}^{u}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}},\quad {\text{if}}}z={\frac {2u{\sqrt {1-u^{4}}}}{1+u^{4}}}}{1+u^{4}}. }}}{{\text{및 }}0\leq qu\leq {\sqrt{\sqrt{2}}-1}}}. 동일한 호의 길이(빨간색 곡선)를 가진 15개의 섹션으로 나누어진 렘니스케이트입니다. 15의 소인수(3과 5)는 모두 페르마 소수이므로, 이 다각형(검은색)은 직선형 가장자리와 나침반을 사용하여 구성할 수 있습니다. 후에 수학자들은 이 결과를 일반화했습니다. 원에 있는 구성 가능한 다각형 과 유사하게, 렘니세이트는 n n 2k 1 p 2 pm {\displaystyle 2^{k}p_{1}p_{2}\cdots p_{m} 가장자리와 나침반 을 사용하여 같은 호 길이의 n개 k 정수 이고 각 p 페르마 소수 입니다. 정리의 "만약" 부분은 닐스 아벨 이 1827년에서 1828년 사이에 증명했고, "만" 부분은 1981년 마이클 로젠 이 증명했습니다.[33] 이와 동일하게 렘니세이트는 φ( n ) {\displaystyle \varphi(n)} {\displaystyle \varphi } 오일러의 토티언트 함수 임)에만 직선 에지와 나침반을 사용하여 같은 호 길이의 n개 렘니스케이트는 이미 그려진 것으로 가정되지 않습니다 . 이 정리는 분할점만 구성하는 것을 말합니다.
r j sl 2 j n {\displaystyle r_{j operatorname {sl} {\dfrac {2j\varpi}{n}} . (x2 y 2 ) 2 x2 y2 {\displaystyle(x^{2} y^{2})^{2 x^{2} y^{2}}
( r j 1 2 ( 1 + r j 2 ) , ( − 1 ) ⌊ 4 j / n ⌋ 1 2 r j 2 ( 1 − r j 2 ) ) , j ∈ { 1 , 2 , … , n } {\displaystyle \left(r_{j}{\tfrac {1}{2}}{{\bigr}}},\bigl(1+r_{j}^{2}{\bigr}}},\(1)^{\left\l floor 4j/n\right\rfloor}{\sqrt {\tfrac {1}{2}}{\bigl(1-r_{j}^{2}{\bigr}}}\right),\quad j\in \{1,2,\ldots,n\}) 여기서 ⌊ ⋅ ⌋ {\ displaystyle \ \cdot \rfloor} 플로어 함수입니다. sl 2 n {\displaystyle \operatorname {sl} {\dfrac {2\varpi} {n}} 아래 를 참조하십시오.
직사각형 탄성체의 원호 길이 렘니세이트 사인은 직사각형 탄성체에서 원호 길이와 x 좌표 사이의 관계를 나타냅니다. 역 렘니세이트 사인은 직사각형 탄성체 의 x 좌표 길이 [34] 이 곡선은 y개
y = ∫ x 1 t 2 d t 1 − t 4 , s = 호를 x = ∫ 0 x d t 1 − t 4 {\displaystyle y=\int _{x}^{1}{\frac {t^{2}}\mathop {\mathrm {d} t}{\sqrt {1-t^{4}}},\quad s=\operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}} 직사각형 탄성체는 1691년 Jacob Bernouli 에 의해 제기된 문제를 해결합니다. 1691년, 바닥 끝에서 수직 방향으로 고정되고 끝에서 수평으로 구부러질 때까지 무게에 의해 아래로 당겨지는 이상적인 유연한 막대의 형태를 묘사합니다. 베르누이가 제안한 해결책은 오일러-베르누이 빔 이론 을 확립시켰으며, 18세기에 오일러에 의해 더욱 발전되었습니다.
타원 특성화 렘니스케이트 타원 함수 및 타원 C {\displaystyle C} x 2 y 2 1 {\displaystyle x^{2} 2y^{2} 1 {\displaystyle } x 2 y 2 {\displaystyle x^{2} ^{2 } 투영 원점 A {\displaystyle A} 점 {\displaystyle C} 거리 {\displaystyle r} 각 BAC {\ BAC }, displaystyle 1,0); 원호 BD {\displaystyle BD} ) {\displaystyle } 매개 변수 u {\displaystyle u}
u = ∫ 0 φ r ( θ ) d θ = ∫ 0 φ d θ 1 + 죄악의 2 θ . {\displaystyle u=\int _{0}^{\varphi }r(\theta )\,\mathrm {d} \theta =\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1+\sin ^{2}\theta }}}} 만약 E {\displaystyle E} D {\displaystyle D} displaystyle F} C {\displaystyle C}
cl u = A F ¯ , 슬 u = D E ¯ , {\displaystyle \operatorname {cl} u={\overline {AF}},\quad \operatorname {sl} u={\overline {DE}} cl ~ u = A F ¯ A C ¯ , 슬 ~ u = A F ¯ F C ¯ . {\displaystyle {\tilde {\operatorname {cl}}}\,u={\overline {AF}},\quad {\tilde {\operatorname {sl}}}\,u={\overline {AF}{\overline {FC}}} 영상 시리즈 아이덴티티 멱급수 원점에서 렘니세이트 사인의 멱급수 확장은[35]
슬 z = ∑ n = 0 ∞ a n z n = z − 12 z 5 5 ! + 3024 z 9 9 ! − 4390848 z 13 13 ! + ⋯ , z < ϖ 2 {\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty}a_{n}z^{n}= z-12{\frac {z^{5}}{5! }}+3024{\frac {z^{9}}{9!}}-4390848{\frac {z^{13}}{13! }}+\cdots ,\quad z <{\tfrac {\varpi}{\sqrt {2}}}} 여기서 계수 displaystyle {n
n ≢ 1 ( 모드의 4 ) ⟹ a n = 0 , {\displaystyle n\not \equiv 1{\pmod {4}}\implies a_{n}=0,} a 1 = 1 , ∀ n ∈ N 0 : a n + 2 = − 2 ( n + 1 ) ( n + 2 ) ∑ i + j + k = n a i a j a k {\displaystyle a_{1}=1,\,\모든 n\in \mathbb {N} _{0}:\,a_{n+2}=-{\frac {2}{(n+1)(n+2)}}\sum _{i+j+k=n}a_{i}a_{j}a_{k}} 여기서 i j k n {\displaystyle j } n {\displaystyle n} 구성 을 나타냅니다. 13 {\displaystyle a_{13}} 0 13 2 11 {\displaystyle 11} 9 1 1 1 9 1 9 {\displaysty le 11=9+1+1=1+9+1=1+1+9}, 11 = 5 + 5 + 1 = 5 = 1 + 5 {\ displaystyle = 5+5+1 = 5+1 = 1+5} ,
a 13 = − 2 12 ⋅ 13 ( a 9 a 1 a 1 + a 1 a 9 a 1 + a 1 a 1 a 9 + a 5 a 5 a 1 + a 5 a 1 a 5 + a 1 a 5 a 5 ) = − 11 15600 . {\displaystyle a_{13}=-{\tfrac {2}{12\cdot 13}}(a_{9}a_{1}a_{9}a_{1}+a_{1}a_{1}a_{1}a_{1}a_{9}+a_{5}a_{1}a_{1}a_{5}a_{1}a_{5}a_{5}a_{1}a_{5}a_{5}=-{\tfrac {11}{15600}}} 확장은 다음과[36]
슬 z = ∑ n = 0 ∞ p 2 n z 4 n + 1 ( 4 n + 1 ) ! , z < ϖ 2 {\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty}p_{2n}{\frac {z^{4n+1}}{(4n+1)! }},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}}} 어디에
p n + 2 = − 12 ∑ j = 0 n ( 2 n + 2 2 j + 2 ) p n − j ∑ k = 0 j ( 2 j + 1 2 k + 1 ) p k p j − k , p 0 = 1 , p 1 = 0. {\displaystyle p_{n+2}=-12\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}p_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}p_{j-k},\quad p_{0}=1,\,p_{1}=0}. 원점에서sl {\ displaystyle {\tilde {\operatorname {sl}}}
슬 ~ z = ∑ n = 0 ∞ α n z n = z − 9 z 3 3 ! + 153 z 5 5 ! − 4977 z 7 7 ! + ⋯ , z < ϖ 2 {\displaystyle {\tilde {\operatorname {sl}}}\,z=\sum _{n=0}^{\infty}\alpha _{n}z^{n}=z-9{\frac {z^{3}}{3! }}+153{\frac{z^{5}}{5!}}-4977{\frac{z^{7}}{7! }}+\cdots ,\quad \left z\right <{\frac {\varpi}{2}}} 여기서 n {\displaystyle n} 경우 α 0 displaystyle \alpha_{n 0}
α n = 2 π ϖ ( − 1 ) ( n − 1 ) / 2 n ! ∑ k = 1 ∞ ( 2 k π / ϖ ) n + 1 으스스한 k π , α n ∼ 2 n + 5 / 2 n + 1 ϖ n + 2 {\displaystyle \alpha_{n}={\sqrt {2}}{\frac {\pi}{\varpi }}{\frac {(-1)^{(n-1)/2}}{n! }}\sum _{k=1}^{\infty}{\frac {(2k\pi /\varpi )^{n+1}}},\cosh k\pi }},\quad \left \alpha_{n}\right \sim 2^{n+5/2}{\frac {n+1}{\varpi ^{n+2}}}. n {\displaystyle n}
확장은 다음과[38]
슬 ~ z = ∑ n = 0 ∞ ( − 1 ) n 2 n + 1 ( ∑ l = 0 n 2 l ( 2 n + 2 2 l + 1 ) s l t n − l ) z 2 n + 1 ( 2 n + 1 ) ! , z < ϖ 2 {\displaystyle {\tilde {\operatorname {sl}}}\,z=\sum _{n=0}^{\infty}{\frac {(-1)^{n}}}\left(\sum _{l=0}^{n}2^{l}}{\binom {2n+2}{2l+1}s_{l}t_{n-l}\right){\frac {z^{2n+1}}{(2n+1)}{(2n+1)}{\frac {z^{n+1)}{(2n+1)}}{(2n+1)! }},\quad \left z\right <{\frac {\varpi}{2}}} 어디에
s n + 2 = 3 s n + 1 + 24 ∑ j = 0 n ( 2 n + 2 2 j + 2 ) s n − j ∑ k = 0 j ( 2 j + 1 2 k + 1 ) s k s j − k , s 0 = 1 , s 1 = 3 , {\displaystyle s_{n+2}=3s_{n+1}+24\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}s_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}s_{j-k},\quad s_{0}=1,\,s_{1}=3,} t n + 2 = 3 t n + 1 + 3 ∑ j = 0 n ( 2 n + 2 2 j + 2 ) t n − j ∑ k = 0 j ( 2 j + 1 2 k + 1 ) t k t j − k , t 0 = 1 , t 1 = 3. {\displaystyle t_{n+2}=3t_{n+1}+3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}t_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}t_{j-k},\quad t_{0}=1,\,t_{1}=3}. 렘니스케이트 코사인의 경우,[39]
cl z = 1 − ∑ n = 0 ∞ ( − 1 ) n ( ∑ l = 0 n 2 l ( 2 n + 2 2 l + 1 ) q l r n − l ) z 2 n + 2 ( 2 n + 2 ) ! = 1 − 2 z 2 2 ! + 12 z 4 4 ! − 216 z 6 6 ! + ⋯ , z < ϖ 2 , {\displaystyle \operatorname {cl} {z}=1-\sum _{n=0}^{\infty}(-1)^{n}\left(\sum _{l=0}^{n}2^{l}{\binom {2n+2}{2l+1}}q_{l}r_{n-l}\right){\frac {z^{2n+2}}{(2n+2)}{{(2n+2)! }}=1-2{\frac {z^{2}}{2! }}}+12{\frac{z^{4}}{4! }}-216{\frac {z^{6}}{6! }}+\cdots ,\quad \left z\right <{\frac {\varpi}{2}},} cl ~ z = ∑ n = 0 ∞ ( − 1 ) n 2 n q n z 2 n ( 2 n ) ! = 1 − 3 z 2 2 ! + 33 z 4 4 ! − 819 z 6 6 ! + ⋯ , z < ϖ 2 {\displaystyle {\tilde {\operatorname {cl}}}\,z=\sum _{n=0}^{\infty}(-1)^{n}2^{n}q_{n}{\frac {z^{2n}}{(2n)! }}=1-3{\frac {z^{2}}{2! }}}+33{\frac{z^{4}}{4! }}-819{\frac{z^{6}}{6! }}+\cdots ,\quad \left z\right <{\frac {\varpi}{2}}} 어디에
r n + 2 = 3 ∑ j = 0 n ( 2 n + 2 2 j + 2 ) r n − j ∑ k = 0 j ( 2 j + 1 2 k + 1 ) r k r j − k , r 0 = 1 , r 1 = 0 , {\displaystyle r_{n+2}=3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}r_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}r_{j-k},\quad r_{0}=1,\,r_{1}=0,} q n + 2 = 3 2 q n + 1 + 6 ∑ j = 0 n ( 2 n + 2 2 j + 2 ) q n − j ∑ k = 0 j ( 2 j + 1 2 k + 1 ) q k q j − k , q 0 = 1 , q 1 = 3 2 . {\displaystyle q_{n+2}={\tfrac {3}{2}}q_{n+1}+6\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}q_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}q_{j-k},\quad q_{0}=1,\,q_{1}={\tfrac {3}{2}}}. 라마누잔의 코스/코스 정체성 라마누잔의 유명한 코스/코스 정체성은 만약
R ( s ) = π ϖ 2 ∑ n ∈ Z cos ( 2 n π s / ϖ ) 으스스한 n π , {\displaystyle R(s)={\frac {\pi}{\varpi {\sqrt {2}}}}\sum_{n\in \mathbb {Z}}{\frac {\cos(2n\pi/\varpi)}{\cosh n\pi}}} 그[37]
R ( s ) − 2 + R ( i s ) − 2 = 2 , 리 s < ϖ 2 , 임 s < ϖ 2 . {\displaystyle R(s)^{-2}+R(is)^{-2}=2,\quad \left \operatorname {Re} s\right <{\frac {\varpi}{2}},\left \operatorname {Im} s\right <{\frac {\varpi}{2}}} 렘니스케이트 함수와 R( s ) {\displaystyle R(s)} . [37] [40]
슬 ~ s = − d d s R ( s ) 임 s < ϖ 2 {\displaystyle {\tilde {\operatorname {sl}}}\,s=-{\frac {\mathrm {d}}{\mathrm {d}}R(s)\quad \left \operatorname {Im}s\right <{\frac {\varpi}{2}}} cl ~ s = d d s 1 − R ( s ) 2 , 리 s − ϖ 2 < ϖ 2 , 임 s < ϖ 2 {\displaystyle {\tilde {\operatorname {cl}}}\,s={\frac {\mathrm {d} s}}{\sqrt {1-R(s)^{2}}},\quad \left \operatorname {Re} s-{\frac {\varpi}{2}}\right <{\frac {\varpi}},\,\left \operatorname {Im} s\right <{\frac {\varpi}{2}} 그리고.
R ( s ) = 1 1 + 슬 2 s , 임 s < ϖ 2 . {\displaystyle R(s)={\frac {1}{\sqrt {1+\operatorname {sl}^{2}s}},\quad \left \operatorname {Im} s\right <{\frac {\varpi}{2}}} 연속분수 z C 0 } {\displaystyle z\in \mathbb {C} \setminus \{0\}
∫ 0 ∞ e − t z 2 cl t d t = 1 / 2 z + a 1 z + a 2 z + a 3 z + ⋱ , a n = n 2 4 ( ( − 1 ) n + 1 + 3 ) {\displaystyle \int _{0}^{\infty}}e^{-tz{\sqrt {2}}\operatorname {cl} t\,\mathrm {d} t={\ cfrac {1/{\sqrt {2}}{z+{\sqrt {2}}{{z+{a_{2}}{z+{\dots}}},\ quad a_{n}={\frac {n^{2}}{(-1)^{n+1}+3}}}}. ∫ 0 ∞ e − t z 2 슬 t cl t d t = 1 / 2 z 2 + b 1 − a 1 z 2 + b 2 − a 2 z 2 + b 3 − ⋱ , a n = n 2 ( 4 n 2 − 1 ) , b n = 3 ( 2 n − 1 ) 2 {\displaystyle \int _{0}^{\infty}}e^{-tz{\sqrt {2}}\operatorname {sl} t\operatorname {cl} t\,\mathrm {d} t={\cfrac {1/2}{z^{2}+b_{1}-{\ cfrac {a_{1}}{z^{2}+b_{2}-{\ cfrac {a_{2}}{z^{2}+b_{3}-\dots }}}},\quad a_{n}=n^{2}(4n^{2}-1),\,b_{n}=3(2n-1)^{2}}}}},\n\n}}}3(2n-1)} 계산법 sl x {\displaystyle \operatorname {sl} x} x x {\displaystyle \pi varpi {\tilde {x}}} sl ( x . {\displaystyle \operatorname {sl}(\varpi {\tilde {x}}/\pi .
쌍곡 직렬 방식:[44] [45] [46]
슬 ( ϖ π x ) = π ϖ ∑ n ∈ Z ( − 1 ) n 으스스한 ( x − ( n + 1 / 2 ) π ) , x ∈ C {\displaystyle \operatorname {sl} \left ({\frac {\varpi}{\pi }}x\right)={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z}{\frac {(-1)^{n}}{\cosh(x-(n+1/2)\pi )}},\quad x\in \mathbb {C}} 1 슬 ( ϖ x / π ) = π ϖ ∑ n ∈ Z ( − 1 ) n 죄스러운 ( x − n π ) = π ϖ ∑ n ∈ Z ( − 1 ) n 죄악의 ( x − n π i ) , x ∈ C {\displaystyle {\frac {1}{\operatorname {sl}(\varpi x/\pi )}}={\frac {\pi}{\varpi }}\sum_{n\in \mathbb {Z}{\frac {(-1)^{n}}{\sinh }{\left(x-n\pi \right) }}={\frac {\pi}{\varpi}}\sum_{n\in \mathbb {Z}}{\frac {(-1)^{n}}{\sin(x-n\pi)}},\quad x\in \mathbb {C}} 푸리에 급수 방법:[47]
슬 ( ϖ π x ) = 2 π ϖ ∑ n = 0 ∞ ( − 1 ) n 죄악의 ( ( 2 n + 1 ) x ) 으스스한 ( ( n + 1 / 2 ) π ) , 임 x < π 2 {\displaystyle \operatorname {sl} {\bigl(}{\frac {\varpi}}{\pi}}x{\Bigr}}={\frac {2\pi}{\varpi}}\sum _{n=0}^{\infty}{\frac {(-1)^{n}\sin((2n+1)x)} {\cosh(((n+1/2)\pi )}},\quad \left \operatorname {Im} x\right <{\frac {\pi}{2}}} cl ( ϖ π x ) = 2 π ϖ ∑ n = 0 ∞ cos ( ( 2 n + 1 ) x ) 으스스한 ( ( n + 1 / 2 ) π ) , 임 x < π 2 {\displaystyle \operatorname {cl} \left ({\frac {\varpi}{\pi }}x\right)={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {\cos(((2n+1)x)}} {\cosh(((n+1/2)\pi )}},\quad \left \operatorname {Im} x\right <{\frac {\pi}{2}}} 1 슬 ( ϖ x / π ) = π ϖ ( 1 죄악의 x − 4 ∑ n = 0 ∞ 죄악의 ( ( 2 n + 1 ) x ) e ( 2 n + 1 ) π + 1 ) , 임 x < π {\displaystyle {\frac {1}{\operatorname {sl}(\varpi x/\pi )}}={\frac {\pi}{\varpi }}\left ({\frac {1}{\sin x}}-4\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x) }{e^{(2n+1)\pi }+1}}\right),\quad \left \operator name {Im} x\right <\pi } 렘니세이트 함수는 다음과 같이 더 빠르게 계산될 수 있습니다.
슬 ( ϖ π x ) = θ 1 ( x , e − π ) θ 3 ( x , e − π ) , x ∈ C cl ( ϖ π x ) = θ 2 ( x , e − π ) θ 4 ( x , e − π ) , x ∈ C {\displaystyle {\begin{aligned}\operatorname {sl} {\Bigl(}{\frac {\varpi}}{\pi}}&={\frac {\theta _{1}}{\left(x,e^{-\pi}\right) }}{{\theta _{3}}{\left(x,e^{-\pi}\right)}}},\quad x\in \mathbb {C} \\\operatorname {cl} {\Bigl(}{\frac {\varpi}}{\pi}}&={\frac {\theta _{2}}{\left(x,e^{\pi}\right) }}{{\theta _{4}}{\left(x,e^{-\pi}\right)}}},\quad x\in \mathbb {C} \end{aligned}}} 어디에
θ 1 ( x , e − π ) = ∑ n ∈ Z ( − 1 ) n + 1 e − π ( n + 1 / 2 + x / π ) 2 = ∑ n ∈ Z ( − 1 ) n e − π ( n + 1 / 2 ) 2 죄악의 ( ( 2 n + 1 ) x ) , θ 2 ( x , e − π ) = ∑ n ∈ Z ( − 1 ) n e − π ( n + x / π ) 2 = ∑ n ∈ Z e − π ( n + 1 / 2 ) 2 cos ( ( 2 n + 1 ) x ) , θ 3 ( x , e − π ) = ∑ n ∈ Z e − π ( n + x / π ) 2 = ∑ n ∈ Z e − π n 2 cos 2 n x , θ 4 ( x , e − π ) = ∑ n ∈ Z e − π ( n + 1 / 2 + x / π ) 2 = ∑ n ∈ Z ( − 1 ) n e − π n 2 cos 2 n x {\displaystyle {\begin{aligned}\theta _{1}(x,e^{-\pi})&=\sum _{n\in \mathbb {Z} }(-1)^{n+1}e^{-\pi(n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi(n+1/2) ^{2}}\sin((2n+1)x), \\\theta _{2}(x,e^{-\pi})&=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z}e^{-\pi (n+1/2) ^{2}}\cos((2n+1)x), \\\theta _{3}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}\cos 2nx,\theta _{4}(x,e^{-\pi })&\sum _{n\in \mathbb {Z} }e^{-\pi (n+1/2+x/\pi )^{2}}=\sum_{n\in \mathbb {Z} ^{n}e^{-\pi n^{2}}\cos 2nx\end{aligned}} 자코비 [48] 세타 함수입니다
렘니세이트 사인의 로그에 대한 푸리에 급수:
ln 슬 ( ϖ π x ) = ln 2 − π 4 + ln 죄악의 x + 2 ∑ n = 1 ∞ ( − 1 ) n cos 2 n x n ( e n π + ( − 1 ) n ) , 임 x < π 2 {\displaystyle \ln \operatorname {sl} \left ({\frac {\pi }{\pi }}x\right)=\ln 2-{\frac {\pi }{4}}+\ln \sin x+2\sum _{n=1}^{\infty }{\frac {(-1)^{n}\cos 2nx}{n(e^{n\pi }+(-1)^{n}}},\quad \left \operatorname {Im}x\right <{\frac {\pi }{2}}} 라마누잔 이 발견한 일련의 동일성은 다음과 같습니다.[49]
ϖ 2 π 2 슬 2 ( ϖ x / π ) = 1 죄악의 2 x − 1 π − 8 ∑ n = 1 ∞ n cos 2 n x e 2 n π − 1 , 임 x < π {\displaystyle {\frac {\varpi ^{2}}{\pi ^{2}\operatorname {sl} ^{2}(\varpi x/\pi )}={\frac {1}{\sin ^{2}x}}-{\frac {1}{\pi }}-8\sum _{n=1}^{\infty}{\frac {n\cos 2nx}{e^{2n\pi }-1}},\quad \left \operatorname {Im} x\right <\pi } 아크탄 슬 ( ϖ π x ) = 2 ∑ n = 0 ∞ 죄악의 ( ( 2 n + 1 ) x ) ( 2 n + 1 ) 으스스한 ( ( n + 1 / 2 ) π ) , 임 x < π 2 {\displaystyle \arctan \operatorname {sl} {\bigl(}{\frac {\varpi}}{\pi}}=2\sum _{n=0}^{\infty}{\frac {\sin((2n+1)x)}{(2n+1)\cosh(((n+1/2))\pi )}},\quad \left \operatorname {Im} x\right <{\frac {\pi}{2}}} 단위 원의sin {\displaystyle \sin} cos {\displaystyle \cos} ) 유사 sl ~ {\ displaystyle {\operatorname {cl}}} cl displaystyle {\operatorname [37] [40] [50]
슬 ~ s = 2 2 π 2 ϖ 2 ∑ n = 1 ∞ n 죄악의 ( 2 n π s / ϖ ) 으스스한 n π , 임 s < ϖ 2 {\displaystyle {\tilde {\operatorname {sl}}}\,s=2{\sqrt {2}}{\frac {\pi ^{2}}}\sum _{n=1}^{\infty}{\frac {n\sin(2n\pi s/\varpi )}{\cosh n\pi }},\quad \left \operatorname {Im} s\right <{\frac {\varpi }{2}}} cl ~ s = 2 π 2 ϖ 2 ∑ n = 0 ∞ ( 2 n + 1 ) cos ( ( 2 n + 1 ) π s / ϖ ) 죄스러운 ( ( n + 1 / 2 ) π ) , 임 s < ϖ 2 {\displaystyle {\tilde {\operatorname {cl}}}\,s={\sqrt {2}}{\frac {\pi ^{2}}}\sum _{n=0}^{\infty }{\frac {(2n+1)\cos((2n+1)\pi s/\varpi )}{\sinh((n+1/2)\pi )}},\quad \left \operatorname {Im} s\right <{\frac {\varpi}{2}}} 슬 ~ s = π 2 ϖ 2 2 ∑ n ∈ Z 죄스러운 ( π ( n + s / ϖ ) ) 으스스한 2 ( π ( n + s / ϖ ) ) , s ∈ C {\displaystyle {\tilde {\operatorname {sl}}}\,s={\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n\in \mathbb {Z}{\frac {\sinh(\pi (n+s/\varpi))}{\cosh ^{2}(\pi (n+s/\varpi))}},\quad s\in \mathbb {C}} cl ~ s = π 2 ϖ 2 2 ∑ n ∈ Z ( − 1 ) n 으스스한 2 ( π ( n + s / ϖ ) ) , s ∈ C {\displaystyle {\tilde {\operatorname {cl}}}\,s={\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n\in \mathbb {Z}{\frac {(-1)^{n}}{\cosh ^{2}(\pi (n+s/\varpi )}},\quad s\in \mathbb {C}} 다른 두 가지 빠른 계산 방법은 다음과 같은 합과 곱 시리즈를 사용합니다.
이 제품은 A Course of Modern Analysis [51]
s l ( ϖ π x ) = 2 e − π / 4 죄악의 x ∏ n = 1 ∞ 1 − 2 e − 2 n π cos 2 x + e − 4 n π 1 + 2 e − ( 2 n − 1 ) π cos 2 x + e − ( 4 n − 2 ) π , x ∈ C {\displaystyle \mathrm {sl} {\frac {\varpi}}{\pi }x{\Bigr )}=2e^{-\pi /4}\sin x\prod _{n=1}^{\infty }{\frac {1-2e^{-2n\pi }\cos 2x+e^{-4n\pi }{1+2e^{-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi },\cos 2x\in \mathbb {C}} c l ( ϖ π x ) = 2 e − π / 4 cos x ∏ n = 1 ∞ 1 + 2 e − 2 n π cos 2 x + e − 4 n π 1 − 2 e − ( 2 n − 1 ) π cos 2 x + e − ( 4 n − 2 ) π , x ∈ C {\displaystyle \mathrm {cl} {\frac {\varpi}}{\pi }x{\Bigr}}=2e^{-\pi /4}\cos x\prod _{n=1}^{\infty }{\frac {1+2e^{-2n\pi }\cos 2x+e^{-4n\pi }{1-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi },\cos 2x\in \mathbb {C}} Peter 와 Jonathan Borwein 형제는 Jacobi 타원함수 일반적인 경우를 언급함으로써 그들의 작업 π과 AGM 에서 유사한 공식을 설명했습니다.
동일한 패턴에서 접선 복제 정리를 사용하여 합 공식을 설정할 수 있습니다.
슬 ( ϖ π x ) = f ( 4 π ϖ 죄악의 x ∑ n = 1 ∞ 으스스한 [ ( 2 n − 1 ) π ] 으스스한 2 [ ( 2 n − 1 ) π ] − cos 2 x ) {\displaystyle {\text{sl}}{\bigl(}{\frac {\varpi}}{\pi }x{\bigr}}=f{\biggl(}{\frac {4\pi}{\varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi]}{\cos ^{2}x}{\biggr}}}}{\cos ^{2}x}}. cl ( ϖ π x ) = f ( 4 π ϖ cos x ∑ n = 1 ∞ 으스스한 [ ( 2 n − 1 ) π ] 으스스한 2 [ ( 2 n − 1 ) π ] − 죄악의 2 x ) {\displaystyle {\text{cl}}{\bigl(}{\frac {\varpi}}{\pi}}x{\bigr}}=f{\biggl(}{\frac {4\pi}{\varpi }}\cos x\sum _{n=1}^{\infty}{\frac {\cosh[(2n-1)\pi]}{\cosh ^{2}[(2n-1)\pi]-\sin ^{2}x}{\biggr}}}}{\cosh ^{2}x}}. 여기서 f x tan 2 arctan x 2 x (1 2 {\displaystyle x) tan (2\arctan 2x/ ^{2})
렘니세이트는 전체 기능의 비율로 기능합니다. 렘니세이트 사인은 복소평면 전체 에서 메로모형 함수이므로, 전체 함수 의 비율로 표기할 수 있습니다. 가우스는 sl 이 0과 극의 분포를 반영하여 다음과 같은 제품 확장을 나타냄을 보여주었습니다.[52]
슬 z = M ( z ) N ( z ) {\displaystyle \operatorname {sl} z={\frac {M(z)}{N(z)}} 어디에
M ( z ) = z ∏ α ( 1 − z 4 α 4 ) , N ( z ) = ∏ β ( 1 − z 4 β 4 ) . {\displaystyle M(z)=z\prod _{\alpha}\left(1-{\frac {z^{4}}{\alpha ^{4}}\right),\quad N(z)=\prod _{\beta }\left(1-{\frac {z^{4}}{\beta ^{4}}\right).} 여기서 α {\displaystyle \alpha } β displaystyle \beta 각각 Re 사분면 있는 sl의 0과 극, Im z displaystyle operatorname {Re} operatorname {Im} \geq } .
렘니세이트 사인에 대한 무한 제품 증명
는 것을 쉽게 알 수 있습니다.
M ′ ( z ) M ( z ) = − ∑ n = 0 ∞ 2 4 n H 4 n z 4 n − 1 ( 4 n ) ! , z < ϖ {\displaystyle {\frac {M'(z)}{M(z)}=-\sum _{n=0}^{\infty}2^{4n}\mathrm {H}_{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left z\right <\varpi } (여기서 Hn {\displaystyle \mathrm {H} _{n}} 렘니스케이트 타원 함수 § 후르비츠 수 에 정의된 후르비츠 수) 및
N ′ ( z ) N ( z ) = ( 1 + i ) M ′ ( ( 1 + i ) z ) M ( ( 1 + i ) z ) − M ′ ( z ) M ( z ) . {\displaystyle {\frac {N'(z)}{N(z)}}=(1+i){\frac {M'((1+i)z)}{M((1+i)z)} }}-{\frac {M'(z)}{M(z)}}. 그러므로
N ′ ( z ) N ( z ) = ∑ n = 0 ∞ 2 4 n ( 1 − ( − 1 ) n 2 2 n ) H 4 n z 4 n − 1 ( 4 n ) ! , z < ϖ 2 . {\displaystyle {\frac {N'(z)}{N(z)}=\sum _{n=0}^{\infty}2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H}_{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}}} 는 것으로 알려져 있습니다.
1 슬 2 z = ∑ n = 0 ∞ 2 4 n ( 4 n − 1 ) H 4 n z 4 n − 2 ( 4 n ) ! , z < ϖ . {\displaystyle {\frac {1}{\operatorname {sl}^{2}z}}=\sum _{n=0}^{\infty}2^{4n}(4n-1)\mathrm {H}_{4n}{\frac {z^{4n-2}}{(4n)!}},\quad \left z\right <\varpi.} 그다음부터.
d d z 슬 ′ z 슬 z = − 1 슬 2 z − 슬 2 z {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}{\operatorname {sl} 'z}{\operatorname {sl} z}=-{\frac {1}{\operatorname {sl}^{2}z}}-\operatorname {sl}^{2}z} 그리고.
슬 2 z = 1 슬 2 z − ( 1 + i ) 2 슬 2 ( ( 1 + i ) z ) {\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\operatorname {sl} ^{2}z}}-{\frac {(1+i)^{2 }}}:{\operatorname {sl}^{2}((1+i)z)}} 우리가 얻는
슬 ′ z 슬 z = − ∑ n = 0 ∞ 2 4 n ( 2 − ( − 1 ) n 2 2 n ) H 4 n z 4 n − 1 ( 4 n ) ! , z < ϖ 2 . {\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl}}=-\sum _{n=0}^{\infty}2^{4n}(2-(-1)^{n}2^{2n})\mathrm {H}_{4n}{\frac {z^{4n-1}}{(4n)!},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}}}. 이런 이유로
슬 ′ z 슬 z = M ′ ( z ) M ( z ) − N ′ ( z ) N ( z ) , z < ϖ 2 . {\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}={\frac {M'(z)}{M(z)}},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}}. 그러므로
슬 z = C M ( z ) N ( z ) {\displaystyle \operatorname {sl} z=C{\frac {M(z)}{N(z)}} z 2 displaystyle } \left z\right {\sqrt {2}} 일부 {\ z C {\displaystyle z\in \mathbb {C} 사용.
절름발이 z → 0 슬 z z = 1 {\displaystyle \lim _{z\to 0}{\frac {\operatorname {sl} z}{z}=1} 는 증명 완료 displaystyle 1} ◼ {\ displaystyle \black square}
가우스는 ln N ( ) 2 {\displaystyle \ln (\varpi pi /2}( 가우스는 M {\displaystyle M} N {\displaystyle N} 그는 또한 {\displaystyle M} 함수 displaystyle N} .
복소 displaystyle M} 복잡한 논쟁은 다양한 색상으로 표현됩니다. 복소 displaystyle N} . 복잡한 논쟁은 다양한 색상으로 표현됩니다. N ( z ) = M ( ( 1 + i ) z ) ( 1 + i ) M ( z ) , z ∉ ϖ Z [ i ] {\displaystyle N(z)={\frac {M((1+i)z)}{(1+i)M(z)}},\quad z\not in \varpi \mathbb {Z} [i]} 그리고.
N ( 2 z ) = M ( z ) 4 + N ( z ) 4 . {\displaystyle N(2z)=M(z)^{4}+N(z)^{4}} 함수 M {\displaystyle M} N {\displaystyle N} [55] [56] [57]
M ( z ) = z − 2 z 5 5 ! − 36 z 9 9 ! + 552 z 13 13 ! + ⋯ , z ∈ C {\displaystyle M(z)=z-2{\frac {z^{5}}{5!}-36{\frac {z^{9}}{9! }}}+552{\frac{z^{13}}{13! }}}+\cdots,\quadz\in \mathbb {C}} N ( z ) = 1 + 2 z 4 4 ! − 4 z 8 8 ! + 408 z 12 12 ! + ⋯ , z ∈ C . {\displaystyle N(z)=1+2{\frac {z^{4}}{4!}}-4{\frac {z^{8}}{8! }}}+408{\frac{z^{12}}{12! }}}+\cdots ,\quadz\in \mathbb {C} . S {\displaystyle S} T {\displaystyle T}
S ( z ) = N ( z 1 + i ) 2 − i M ( z 1 + i ) 2 , T ( z ) = S ( i z ) . {\displaystyle S(z)=N\left({\frac {z}{1+i}}\right)^{2}-iM\left({\frac {z}{1+i}}\right)^{2},\quad T(z)=S(iz)} 그렇다면 렘니스케이트 코사인은 다음과 같이 쓸 수 있습니다.
cl z = S ( z ) T ( z ) {\displaystyle \operatorname {cl} z={\frac {S(z)}{T(z)}} 어디서[58]
S ( z ) = 1 − z 2 2 ! − z 4 4 ! − 3 z 6 6 ! + 17 z 8 8 ! − 9 z 10 10 ! + 111 z 12 12 ! + ⋯ , z ∈ C {\displaystyle S(z)=1-{\frac {z^{2}}{2! }}-{\frac {z^{4}}{4! }}-3{\frac {z^{6}}{6! }}}+17{\frac {z^{8}}{8! }}-9{\frac {z^{10}}{10! }}+111{\frac{z^{12}}{12! }}}+\cdots,\quadz\in \mathbb {C}} T ( z ) = 1 + z 2 2 ! − z 4 4 ! + 3 z 6 6 ! + 17 z 8 8 ! + 9 z 10 10 ! + 111 z 12 12 ! + ⋯ , z ∈ C . {\displaystyle T(z)=1+{\frac {z^{2}}{2! }}-{\frac {z^{4}}{4! }}}+3{\frac {z^{6}}{6! }}}+17{\frac {z^{8}}{8! }}}+9{\frac {z^{10}}{10! }}+111{\frac{z^{12}}{12! }}}+\cdots ,\quadz\in \mathbb {C} . 더 나아가,
M ( 2 z ) = 2 M ( z ) N ( z ) S ( z ) T ( z ) , {\displaystyle M(2z)=2M(z)N(z)S(z)T(z),} S ( 2 z ) = N ( z ) 4 − 2 N ( z ) 2 M ( z ) 2 − M ( z ) 4 , {\displaystyle S(2z)=N(z)^{4}-2N(z)^{2}M(z)^{2}-M(z)^{4}} T ( 2 z ) = N ( z ) 4 + 2 N ( z ) 2 M ( z ) 2 − M ( z ) 4 {\displaystyle T(2z)=N(z)^{4}+2N(z)^{2}M(z)^{2}-M(z)^{4}} 피타고라스의 정체성과
M ( z ) 2 + S ( z ) 2 = N ( z ) 2 , {\displaystyle M(z)^{2}+S(z)^{2}=N(z)^{2}} M ( z ) 2 + N ( z ) 2 = T ( z ) 2 {\displaystyle M(z)^{2}+N(z)^{2}=T(z)^{2}} z C {\displaystyle z\in \mathbb {C}} .
렘니세이트 함수를 전체 함수의 비율로 표현하는 대안적인 방법은 세타 함수를 포함합니다(렘니세이트 타원 함수 § 계산 방법 참조; 세타 함수와 위 함수는 동등하지 않습니다).
다른 기능과의 관계 바이어슈트라스와 야코비 타원함수와의 관계 렘니세이트 함수는 바이어슈트라스 타원 함수 ℘(z ; 1 , 0 ) {\displaystyle \wp(z; 1, 0)}(" 불변량 g 이 격자는 기본 주기 ω 1 2 , {\displaystyle \omega_{1 sqrt {2}}\varpi ,}, 2 i 1 {\displaystyle \omega_{2 i\omega_{1}} . Weierstrass 함수의 연결 상수는 e 1 2 e 2 0 , 3 2 . {\displaystyle e_{1 tfrac {1}{2}},\ e_{2 0,\ e_{3 tfrac {1}{2}}}
g a g 0인 Weiersstrass 타원 함수의 관련 사례는 스케일링 변환에 의해 처리될 수 있습니다.그러나 여기에는 복잡한 숫자가 포함될 수 있습니다. 실수 내에 남아 있으려면 a 0 0 의 두 가지 경우를 고려해야 합니다. 주기 평행사변형 은 정사각형 또는 마름모꼴 입니다. Weiersstrass 타원 함수 ( z ; 1 , 0 {\displaystyle \wp(z;-1,0)}
렘니세이트 사인의 제곱은 다음과 같이 나타낼 수 있습니다.
슬 2 z = 1 ℘ ( z ; 4 , 0 ) = i 2 ℘ ( ( 1 − i ) z ; − 1 , 0 ) = − 2 ℘ ( 2 z + ( i − 1 ) ϖ 2 ; 1 , 0 ) {\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp(z;4,0)}={\frac {i}{2\wp(((1-i)z;-1,0)}={-2\wp}{\left ({\sqrt {2}}z+(i-1){\frac {\varpi}{\sqrt {2};1,0\right) }} 여기서 ℘ {\displaystyle \wp} g g 또 다른 표현은
슬 2 z = ϖ 2 ℘ ( z / ϖ , i ) {\displaystyle \operatorname {sl} ^{2}z={\frac {\varpi ^{2}}{\wp(z/\varpi,i)}} 여기서 ℘ {\displaystyle \wp} {\displaystyle \tau} . 유리 함수 입니다.
슬 z = ( i − 1 ) ℘ ( ( 1 + i ) z ; 1 / 4 , 0 ) ℘ ′ ( ( 1 + i ) z ; 1 / 4 , 0 ) {\displaystyle \operatorname {sl} z=(i-1){\frac {\wp((1+i)z;1/4,0)}{\wp '(1+i)z;1/4,0)}} 여기서 ℘ {\displaystyle \wp} g g 주기 비율 τ {\displaystyle \tau} .
슬 z = 2 ϖ ( i − 1 ) ℘ ( ( 1 + i ) z / ( 2 ϖ ) , i ) ℘ ′ ( ( 1 + i ) z / ( 2 ϖ ) , i ) . {\displaystyle \operatorname {sl} z=2\varpi(i-1){\frac {\wp((1+i)z/(2\varpi),i)}{\wp '(1+i)z/(2\varpi)}}} 렘니세이트 함수는 야코비 타원 함수 로도 쓸 수 있습니다. 양의 실제 타원 계수를 가진sn {\displaystyle \operatorname {sn} cd {\displaystyle \operatorname {cd}}은( 또는 모듈러스 i sn {\displaystyle \operatorname {sn}} cd {\ displaystyle operatorname {cd}( 1/2 sd displaystyle operatorname {sd} cn {\displaystyle \operatorname cn}) . [62] [63]
슬 z = sn ( z ; i ) = sc ( z ; 2 ) = 1 2 sd ( 2 z ; 1 2 ) {\displaystyle \operatorname {sl} z=\operatorname {sn}(z;i)=\operatorname {sc}(z;{\sqrt {2}}={{\tfrac {1}{\sqrt {2}}\operatorname {sd}\left ({\sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right)} cl z = 씨디 ( z ; i ) = dn ( z ; 2 ) = cn ( 2 z ; 1 2 ) {\displaystyle \operatorname {cl} z=\operatorname {cd}(z;i)=\operatorname {dn}(z;{\sqrt {2}}={\operatorname {cn}\left ({\sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right)} 여기서 두 번째 인수는 타원 모듈러스 k {\displaystyle k} .
함수 sl {\ displaystyle {\tilde {\operatorname }}}, cl displaystyle {\tilde {\ cl}}}
슬 ~ z = 씨디 ( z ; i ) sd ( z ; i ) = dn ( z ; 2 ) sn ( z ; 2 ) = 1 2 cn ( 2 z ; 1 2 ) sn ( 2 z ; 1 2 ) , {\displaystyle {\tilde {\operatorname {sl}}}\,z=\operatorname {cd}(z;i)\operatorname {sd}(z;i)=\operatorname {dn}(z;{\sqrt {2})\operatorname {sn}(z;{\sqrt {2})={\tfrac {1}{\sqrt {2}}\operatorname {cn}\left ({\sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right)\operatorname {sn}\left ({\sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right},} cl ~ z = 씨디 ( z ; i ) nd ( z ; i ) = dn ( z ; 2 ) cn ( z ; 2 ) = cn ( 2 z ; 1 2 ) dn ( 2 z ; 1 2 ) . {\displaystyle {\tilde {\operatorname {cl}}}\,z=\operatorname {cd}(z;i)\operatorname {nd}(z;i)=\operatorname {dn}(z;{\sqrt {2})\operatorname {cn}(z;{\sqrt {2})=\operatorname {cn} \left ({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}\right)\operatorname {dn} \left ({\sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right}. 모듈식 람다 함수와의 관계 렘니세이트 사인은 모듈러 람다 함수 의 값을 계산하는 데 사용할 수 있습니다.
∏ k = 1 n 슬 ( 2 k − 1 2 n + 1 ϖ 2 ) = λ ( ( 2 n + 1 ) i ) 1 − λ ( ( 2 n + 1 ) i ) 8 {\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl}}{\left ({\frac {2k-1}{2n+1}}{\frac {\varpi}{2}}\right) }= {\sqrt[{8}]{\frac {\lambda((2n+1)i)}{1-\lambda((2n+1)i) }}}} 예를 들어,
슬 ( 1 14 ϖ ) 슬 ( 3 14 ϖ ) 슬 ( 5 14 ϖ ) = λ ( 7 i ) 1 − λ ( 7 i ) 8 = 태닝한 ( 1 2 arccsc ( 1 2 8 7 + 21 + 1 2 7 + 1 ) ) 슬 ( 1 18 ϖ ) 슬 ( 3 18 ϖ ) 슬 ( 5 18 ϖ ) 슬 ( 7 18 ϖ ) = λ ( 9 i ) 1 − λ ( 9 i ) 8 = 태닝한 ( π 4 − 아크탄 ( 2 2 3 − 2 3 − 2 2 − 3 3 + 3 − 1 12 4 ) ) {\displaystyle {\begin{aligned}&{\operatorname {sl}}{\bigl(}{\tfrac {1}{14}}\varpi {\bigr )}\, {\operatorname {sl}{\bigl(}{\tfrac {3}{14}\varpi {\bigr )}\, {\operatorname {sl}}{\bigl(}{\tfrac {5}{14}}\varpi {\bigr}}\[7mu]&\quad {}={\sqrt[{8}}{\frac {\lambda(7i)}{1-\lambda(7i)}={\tfrac {1}{2}}\operatorname {arccsc}}{\Bigl(}{\tfrac {1}{2}}}{\sqrt {8{\sqrt {7}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+{\Bigr}}\[18mu]& {\operatorname {sl}}{\bigl(}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl}{\bigr )}{\bigl(}{\tfrac {3}{18}\varpi {\bigr )}\,{\operatorname {sl}{\bigl(}{\tfrac {5}{18}\varpi {\bigr )}\, {\operatorname {sl}}{\bigl(}{\tfrac {7}{18}}\varpi {\bigr )}\[-3mu]&\quad {}={\sqrt[{8}}{\frac {\lambda(9i)}{1-\pi }}={\tan }{\biggl(}{\frac {\pi }{4}}-{\arctan }{\biggl(}{\frac {2{\sqrt[{3}}}-{\sqrt{3}}-2{\sqrt[{3}}}-2{\sqrt{3}}-2{\sqrt{3}}}+{\sqrt{3}}-1}{\sqrt[{4}}{12}}{\biggr )}{\end{aligned}} 역함수 렘니세이트 사인의 역함수는 렘니세이트 아크사인이며, 다음과 같이 정의됩니다.
호를 x = ∫ 0 x d t 1 − t 4 . {\displaystyle \operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}} 또한 기하학 함수로 나타낼 수도 있습니다.
호를 x = x 2 F 1 ( 1 2 , 1 4 ; 5 4 ; x 4 ) . {\displaystyle \operatorname {arcsl} x=x\,{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{4}};{\tfrac {5}{4};x^{4}\right).} 렘니세이트 코사인의 역함수는 렘니세이트 아르코신입니다. 이 함수는 다음 식으로 정의됩니다.
아크클 x = ∫ x 1 d t 1 − t 4 = 1 2 ϖ − 호를 x {\displaystyle \operatorname {arccl} x=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\tfrac {1}{2}}\varpi -\operatorname {arcsl} x} 구간 - 1 ≤ x ≤ {\displaystyle -1\leq x\leq 1 경우 sl arcsl x {\displaystyle \operatorname {sl} \operatorname {arcsl} x \operatorname {cl} \operatorname {arccl} x}
렘니세이트 아크 길이를 절반으로 줄이는 경우 다음 공식이 유효합니다.
슬 ( 1 2 호를 x ) = 죄악의 ( 1 2 호신 x ) 뒤지다 ( 1 2 arsinh x ) 슬 ( 1 2 호를 x ) 2 = 태닝한 ( 1 4 호신 x 2 ) {\displaystyle {\begin{aligned}{\operatorname {sl}}{\bigl(}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr}&={\sin}{\bigl(}{\tfrac {1}{2}}\arcsin x{\bigr}}\, {\operatorname {sech}}{\bigl(}{\tfrac {1}{2}}\operatorname {arsinh} x{\bigr}}\{\operatorname {sl}{\bigl(}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr}^{2}&={\tan }{\bigl(}){\bigl({tfrac {1}{4}}\arcsin x^{2}{\bigr}\end{aligned}} 또한 이른바 쌍곡선 렘니세이트 영역 기능이 있습니다.
쓱 ( x ) = ∫ 0 x 1 y 4 + 1 d y = 1 2 F [ 2 아크탄 ( x ) ; 1 2 2 ] {\displaystyle \operatorname {aslh}(x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2},{\bigr ]}} 패거리 ( x ) = ∫ x ∞ 1 y 4 + 1 d y = 1 2 F [ 2 아궁이 ( x ) ; 1 2 2 ] {\displaystyle \operatorname { aclh}(x)=\int _{x}^{\infty}}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\operatorname {arccot}(x);{\frac {1}{2}{\sqrt {2}},{\bigr ]}} 패거리 ( x ) = ϖ 2 − 쓱 ( x ) {\displaystyle \operatorname { aclh}(x)={\frac {\varpi}{\sqrt {2}}-\operatorname {aslh}(x)} 쓱 ( x ) = 2 호를 [ x ( x 4 + 1 + 1 ) − 1 / 2 ] {\displaystyle \operatorname {aslh}(x)={\sqrt {2}}\operatorname {arcsl} {\bigl [}x ({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]} 호를 ( x ) = 2 쓱 [ x ( 1 + 1 − x 4 ) − 1 / 2 ] {\displaystyle \operatorname {arcsl}(x)={\sqrt {2}}\operatorname {aslh} {\bigl [}x(1+{\sqrt {1-x^{4}})^{-1/2}{\bigr ]}} 타원 적분을 이용한 표현 렘니세이트 아크신 및 렘니세이트 아크코신은 범례 재형성으로 표현할 수도 있습니다.
이러한 기능은 첫 번째 유형의 불완전한 타원 적분 을 사용하여 직접 표시할 수 있습니다.
호를 x = 1 2 F ( 호신 2 x 1 + x 2 ; 1 2 ) {\displaystyle \operatorname {arcsl} x={\frac {1}{\sqrt {2}}F\left({\arcsin}}{\frac {\sqrt {2}}x}{\sqrt {1+x^{2}}{\sqrt {1+x}} }}};{\frac {1}{\sqrt {2}}\right)} 호를 x = 2 ( 2 − 1 ) F ( 호신 ( 2 + 1 ) x 1 + x 2 + 1 ; ( 2 − 1 ) 2 ) {\displaystyle \operatorname {arcsl} x=2({\sqrt {2}-1) F\left({\arcsin}}{\frac {({\sqrt {2}}+1)x}{\sqrt {1+x^{2} }}}+1}};({\sqrt {2}-1)^{2}\right)} 렘니스케이트의 아크 길이는 타원 의 아크 길이(두 번째 종류의 타원 적분으로 계산)만을 사용하여 표현할 수도 있습니다.
호를 x = 2 + 2 2 E ( 호신 ( 2 + 1 ) x 1 + x 2 + 1 ; ( 2 − 1 ) 2 ) − E ( 호신 2 x 1 + x 2 ; 1 2 ) + x 1 − x 2 2 ( 1 + x 2 + 1 + x 2 ) {\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}{2}}}E\left({\arcsin}{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}{\sqrt {1+x}}{2 }}+1}};({\sqrt {2}-1)^{2}\right)\[5mu]&\E\left({\arcsin}}{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2} }}};{\frac {1}{\sqrt {2}}\right)+{\frac {x{\sqrt {1-x^{2}}}}:{\sqrt {2}}(1+x^{2})+{\sqrt {1+x^{2}}}\end{aligned}} 렘니세이트 아르코신은 다음과 같은 식을 갖습니다.
아크클 x = 1 2 F ( 아코코 x ; 1 2 ) {\displaystyle \operatorname {arccl} x={\frac {1}{\sqrt {2}}}F\left(\arccos x;{\frac {1}{\sqrt {2}}\right)} 통합사용 렘니세이트 아크신은 많은 기능을 통합하는 데 사용될 수 있습니다. 다음은 중요한 적분 목록입니다(적분 상수는 생략됨).
∫ 1 1 − x 4 d x = 호를 x {\displaystyle \int {\frac {1}{\sqrt {1-x^{4}}},\mathrm {d} x=\operator name {arcsl} x} ∫ 1 ( x 2 + 1 ) ( 2 x 2 + 1 ) d x = 호를 x x 2 + 1 {\displaystyle \int {\frac {1}{\sqrt {(x^{2}+1)(2x^{2}+1)}}\,\mathrm {d} x={\operatorname {arcsl}}{\frac {x}{x^{2}+1}}} ∫ 1 x 4 + 6 x 2 + 1 d x = 호를 2 x x 4 + 6 x 2 + 1 + x 2 + 1 {\displaystyle \int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}\,\mathrm {d} x={\operatorname {arcsl}}{\frac {\sqrt {2}}{\sqrt {x^{4}+6x^{2}}+x^{2}+1}}}}. ∫ 1 x 4 + 1 d x = 2 호를 x x 4 + 1 + 1 {\displaystyle \int {\frac {1}{\sqrt {x^{4}+1}}\,\mathrm {d} x= {{\sqrt {2}\operatorname {arcsl}}{\frac {x}{\sqrt {x^{4}+1}}}} ∫ 1 ( 1 − x 4 ) 3 4 d x = 2 호를 x 1 + 1 − x 4 {\displaystyle \int {\frac {1}{\sqrt[{4}}{(1-x^{4})^{3}}}\,\mathrm {d} x= {{\sqrt {2}}\operatorname {arcsl}}{\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}} ∫ 1 ( x 4 + 1 ) 3 4 d x = 호를 x x 4 + 1 4 {\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3 }}}\,\mathrm {d} x={\operatorname {arcsl}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}} ∫ 1 ( 1 − x 2 ) 3 4 d x = 2 호를 x 1 + 1 − x 2 {\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2}^{3}}}\,\mathrm {d} x={2\operatorname {arcsl}}{\frac {x}{1+{\sqrt {1-x^{2}}}}} ∫ 1 ( x 2 + 1 ) 3 4 d x = 2 호를 x x 2 + 1 + 1 {\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3 }}}\,\mathrm {d} x={2\operatorname {arcsl}}{\frac {x}{\sqrt {x^{2}+1}}+1}}} ∫ 1 ( a x 2 + b x + c ) 3 4 d x = 2 2 4 a 2 c − a b 2 4 호를 2 a x + b 4 a ( a x 2 + b x + c ) + 4 a c − b 2 {\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c) ^{3}}}\,\mathrm {d} x= {{\frac {2{\sqrt {2}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}\operatorname {arcsl}}{\frac {2ax+b}{\sqrt {4a(ax^{2}+bx+c) }}+{\sqrt{4ac-b^{2}}}}}. ∫ 뒤지다 x d x = 2 호를 탄 1 2 x {\displaystyle \int {\sqrt {\operatorname {sech} x}}\,\mathrm {d} x={2\operatorname {arcsl}}\tanh {\tfrac {1}{2} x} ∫ 초 x d x = 2 호를 태닝한 1 2 x {\displaystyle \int {\sqrt {\sec x}}\,\mathrm {d} x={2\operatorname {arcsl}}\tan {\tfrac {1}{2}}x} 쌍곡 렘니세이트 함수 기초정보 실제 인수에 적용되는 쌍곡 렘니세이트 사인(빨간색) 및 쌍곡 렘니세이트 코사인(보라색)은 삼각 접선(흰색 점선 빨간색)과 비교됩니다. 복소 평면에서 쌍곡 렘니세이트 사인. 어두운 영역은 0을 나타내고 밝은 영역은 극을 나타냅니다. 복잡한 논쟁은 다양한 색상으로 표현됩니다. 편의를 위해 σ = 2 displaystyle sqrt 2}}\varpi displaystyle {\displaystyle \pi}( σ {\displaystyle \sigma ( , 3 displaystyle 3.7081 })
쌍곡 렘니세이트 사인(slh )과 코사인(clh )은 다음과 같이 타원 적분의 역으로 정의할 수 있습니다.
z = ∗ ∫ 0 슬며시쓱 z d t 1 + t 4 = ∫ clh z ∞ d t 1 + t 4 {\displaystyle z\mathrel {\overset {*}{=}} \int _{0}^{\operatorname {slh} z}{\frac {\mathrm {d} t}{\sqrt {1+t^{4 }}}}=\int _{\operatorname {clh} z}^{\infty}{\frac {\mathrm {d} t}{\sqrt {1+t^{4 }}}}} 여기서 ( ) {\displaystyle(*)}, z {\displaystyle z} { 2, 2, i 2} displaystyle \{\sigma /2,\sigma /2,-\sigma /2,-\sigma /2\} .
완전한 적분은 다음과 같은 값을 갖습니다.
∫ 0 ∞ d t t 4 + 1 = 1 4 B ( 1 4 , 1 4 ) = σ 2 = 1.85407 46773 01371 … {\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{4}+1}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}{\bigr )}={\frac {\sigma }{2}}=1.85407\;46773\;01371\ldots } 따라서 정의된 두 함수는 서로 다음과 같은 관계를 갖습니다.
슬며시쓱 z = clh ( σ 2 − z ) {\displaystyle \operatorname {slh} z={\operatorname {clh}}{\Bigl(}{\frac {\sigma }{2}}-z{\Bigr}}} 쌍곡 렘니세이트 사인과 쌍곡 렘니세이트 코사인의 곱은 다음과 같습니다.
슬며시쓱 z clh z = 1 {\displaystyle \operatorname {slh} z\,\operatorname {clh} z=1} 함수 slh {\displaystyle \operatorname {slh}} clh displaystyle \operatorname {clh}} displaystyle sigma,\sigma \} .
쌍곡 렘니세이트 함수는 렘니세이트 사인과 렘니세이트 코사인으로 표현할 수 있습니다.
슬며시쓱 ( 2 z ) = ( 1 + cl 2 z ) 슬 z 2 cl z {\displaystyle \operatorname {slh} {\bigl(}{\sqrt {2}}z{\bigr}}={\frac {(1+\operatorname {cl}^{2}z)\operatorname {sl}{\sqrt {2}}\operatorname {cl}z}} clh ( 2 z ) = ( 1 + 슬 2 z ) cl z 2 슬 z {\displaystyle \operatorname {clh} {\bigl(}{\sqrt {2}}z{\bigr )}={\frac {(1+\operatorname {sl}^{2}z)\operatorname {cl}{\sqrt {2}\operatorname {sl}z}} 그러나 야코비 타원 함수 와 타원 모듈러스 1제곱근 2제곱근의 관계도 있습니다.
슬며시쓱 z = sn ( z ; 1 / 2 ) 씨디 ( z ; 1 / 2 ) {\displaystyle \operatorname {slh} z={\frac {\operatorname {sn}(z;1/{\sqrt {2}})}{\operatorname {cd}(z;1/{\sqrt {2}}}} clh z = 씨디 ( z ; 1 / 2 ) sn ( z ; 1 / 2 ) {\displaystyle \operatorname {clh} z={\frac {\operatorname {cd}(z;1/{\sqrt {2}})}{\operatorname {sn}(z;1/{\sqrt {2}}}} 쌍곡 렘니세이트 사인은 렘니세이트 사인과 다음과 같은 가상의 관계를 갖습니다.
슬며시쓱 z = 1 − i 2 슬 ( 1 + i 2 z ) = 슬 ( − 1 4 z ) − 1 4 {\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}\operatorname {sl} \left ({\frac {1+i}{\sqrt {2}}z\right)={\frac {\operatorname {sl} \left ({\sqrt[{4}]{-1}z\right)}{\sqrt[{4}}{-1}}}} 이는 쌍곡선과 삼각 사인의 관계와 유사합니다.
죄스러운 z = − i 죄악의 ( i z ) = 죄악의 ( − 1 2 z ) − 1 2 {\displaystyle \sinh z=-i\sin(iz) ={\frac {\sin \left ({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}} 페르마 곡선과의 관계 쌍곡선 렘니스케이트 접선과 코탄젠트 이 이미지는 표준화된 4차 페르마 원곡선을 보여줍니다.
관계 4 y 4 1 {\displaystyle x^{4} y^{4 1} 4차 페르마 곡선 x 4 4 {\displaystyle x^{4} ^{4 1 }(때로는 꼬임꼴이 라고도 함)에서 쌍곡 렘니세이트 사인과 코사인은 단위 원 x 2 2 {\displaystyle x^{2} ^{2 1 }(2차 원점과 곡선의 한 점이 L선 L선 x 1 {\displaystyle 1} . {\displaystyle \pi} x 2 y 2 {\ pi 유형 x^{2}+y^{2}=1 x 4 4 = {\displaystyle ^{4}+y^{4 = 1} σ {\displaystyle sigma .
M ( 1 , 1 / 2 ) = π σ {\displaystyle M(1,1/{\sqrt {2}})={\frac {\pi}{\sigma }} 여기서 M {\displaystyle M} 산술 기하학 평균 입니다.
쌍곡 렘니스케이트 사인은 인수 덧셈 항등식을 만족합니다.
슬며시쓱 ( a + b ) = 슬며시쓱 a 슬며시쓱 ′ b + 슬며시쓱 b 슬며시쓱 ′ a 1 − 슬며시쓱 2 a 슬며시쓱 2 b {\displaystyle \operatorname {slh}(a+b)={\frac {\operatorname {slh} a\operatorname {slh} 'b+\operatorname {slh} b\operatorname {slh} 'a}{1-\operatorname {slh} ^{2}a\,\operatorname {slh} ^{2}b}} u {\displaystyle u} slh {\displaystyle \operatorname {slh}} clh {\displaystyle \operatorname {clh}}
d d u 슬며시쓱 ( u ) = 1 + 슬며시쓱 ( u ) 4 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} u}\operatorname {slh}(u)={\sqrt {1+\operatorname {slh}(u)^{4}}}
d d u clh ( u ) = − 1 + clh ( u ) 4 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d}u}\operatorname {clh}(u)=-{\sqrt {1+\operatorname {clh}(u)^{4}}}}
d d u 1 2 arsinh [ 슬며시쓱 ( u ) 2 ] = 슬며시쓱 ( u ) {\displaystyle {\frac {\mathrm {d} u}\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {slh}(u)^{2}{\bigr ]}=\operatorname {slh}(u)
d d u − 1 2 arsinh [ clh ( u ) 2 ] = clh ( u ) {\displaystyle {\frac {\mathrm {d} u}-\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {clh}(u)^{2}{\bigr ]}=\operatorname {clh}(u)
또한 쌍곡 렘니케이트 접선 및 쌍곡 렘니케이트 코안젠탈의 추가 기능이 있습니다.
함수 tlh와 ctlh는 다음과 같이 언급된 미분 방정식에 설명된 항등식을 충족합니다.
tlh ( 2 u ) = 죄악의 4 ( 2 u ) = 슬 ( u ) cl 2 u + 1 슬 2 u + cl 2 u {\displaystyle {\text{tlh}}({\sqrt {2}}\,u)=\sin _{4}({\sqrt {2}}\,u)=\operatorname {sl}(u){\sqrt {\operatorname {cl}^{2}u+1}{\operatorname {sl}^{2}u+\operatorname {cl}} ctlh ( 2 u ) = cos 4 ( 2 u ) = cl ( u ) 슬 2 u + 1 슬 2 u + cl 2 u {\displaystyle {\text{ctlh}}({\sqrt {2}}\,u)=\cos _{4}({\sqrt {2}}\,u)=\operatorname {cl}(u){\sqrt {\operatorname {sl}^{2}u+1}{\operatorname {sl}^{2}u+\operatorname {cl}} 기능적 지정 sl은 렘니시틱 사인을 의미하고 지정 cl은 렘니시틱 코사인을 의미합니다. 또한 야코비 타원 함수 와의 관계는 다음과 같습니다.
tlh ( u ) = sn ( u ; 1 2 2 ) 씨디 ( u ; 1 2 2 ) 4 + sn ( u ; 1 2 2 ) 4 4 {\displaystyle {\text{tlh}}(u)={\frac {{\text{sn}}(u;{\tfrac {1}{2}}}{\text{cd}}(u;{\tfrac {1}{2}}}^{4}+{\tfrac {2}}^{u;{\tfrac {1}{2}}^{4}} ctlh ( u ) = 씨디 ( u ; 1 2 2 ) 씨디 ( u ; 1 2 2 ) 4 + sn ( u ; 1 2 2 ) 4 4 {\displaystyle {\text{ctlh}}(u)={\frac {{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}}}{\text{cd}}{(u;{\tfrac {1}{2}}^{4}+{\tfrt {2}}^{u;{\tfrac {1}{2}}^{4}}} u {\displaystyle u} tlh displaystyle \operatorname {tlh}} ctlh displaystyle \operatorname {ctlh}}
d d u tlh ( u ) = ctlh ( u ) 3 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} u}\operator name {tlh}(u)=\operator name {ctlh}(u)^{3}
d d u ctlh ( u ) = − tlh ( u ) 3 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} u}\operator name {ctlh}(u)=-\operator name {tlh}(u)^{3}
∫ 0 ϖ / 2 tlh ( u ) d u = ϖ 2 {\displaystyle \int _{0}^{\varpi /{\sqrt {2}}\operatorname {tlh}(u)\,\mathrm {d}u={\frac {\varpi}{2}}
∫ 0 ϖ / 2 ctlh ( u ) d u = ϖ 2 {\displaystyle \int _{0}^{\varpi /{\sqrt {2}}\operatorname {ctlh}(u)\,\mathrm {d}u={\frac {\varpi}{2}}
쌍곡 렘니스케이트 함수의 유도 4차 페르마 곡선 x 4 4 1 {\displaystyle ^{4} y^{4 1} slh {\displaystyle \operatorname {slh}} clh {\displaystyle operatorname {clh}} 달리 displaystyle sin _{4 cos displaystyle cos _{4 [67] 이 초입의 수평 및 수직 좌표는 밀폐된 면적의 2배인 w = 2A에 종속되므로 다음 조건을 충족해야 합니다.
x ( w ) 4 + y ( w ) 4 = 1 {\displaystyle x(w)^{4}+y(w)^{4}=1} d d w x ( w ) = − y ( w ) 3 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} w}x(w)=-y(w)^{3} d d w y ( w ) = x ( w ) 3 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} w}y(w)=x(w)^{3}} x ( w = 0 ) = 1 {\displaystyle x(w=0)=1} y ( w = 0 ) = 0 {\displaystyle y(w=0)=0} 이 방정식 체계에 대한 해결책은 다음과 같습니다.
x ( w ) = cl ( 1 2 2 w ) [ 슬 ( 1 2 2 w ) 2 + 1 ] 1 / 2 [ 슬 ( 1 2 2 w ) 2 + cl ( 1 2 2 w ) 2 ] − 1 / 2 {\displaystyle x(w)=\operatorname {cl}({\tfrac {1}{2}}{\sqrt {2}w)[\operatorname {sl}({\tfrac {1}{2}}{\sqrt {2}+1]^{1/2}[\operatorname {sl}({\tfrac {1}{2}}{\sqrt {2}w)^{2}+\operatorname {cl}({\tfrac {1}{2}}^{\sqrt {2}}^{-1/2}}^ y ( w ) = 슬 ( 1 2 2 w ) [ cl ( 1 2 2 w ) 2 + 1 ] 1 / 2 [ 슬 ( 1 2 2 w ) 2 + cl ( 1 2 2 w ) 2 ] − 1 / 2 {\displaystyle y(w)=\operatorname {sl}({\tfrac {1}{2}}{\sqrt {2}w)[\operatorname {cl}({\tfrac {1}{2}}{\sqrt {2}+1]^{1/2}[\operatorname {sl}({\tfrac {1}{2}}{\sqrt {2}w)^{2}+\operatorname {cl}({\tfrac {1}{2}}^{\sqrt {2}}^{-1/2}}^ 따라서 몫에는 다음이 적용됩니다.
y ( w ) x ( w ) = 슬 ( 1 2 2 w ) [ cl ( 1 2 2 w ) 2 + 1 ] 1 / 2 cl ( 1 2 2 w ) [ 슬 ( 1 2 2 w ) 2 + 1 ] 1 / 2 = 슬며시쓱 ( w ) {\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl}({1}{2}}{\sqrt {2}w)[\operatorname {cl}({\tfrac {1}{2}}{\sqrt {2}w)^{2}+1}^{\operatorname {cl}({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl}({\tfrac {1}{2}}^{\sqrt {2}w)^{1/2}}=\operatorname {sl}(w) 함수 x(w)와 y(w)를 코탄젠트 쌍곡 렘니스카투스 및 쌍곡 탄젠트 라고 합니다.
x ( w ) = ctlh ( w ) {\displaystyle x(w)={\text{ctlh}}(w)} y ( w ) = tlh ( w ) {\displaystyle y(w)={\text{tlh}}(w)} 스케치는 또한 Areasinus 쌍곡 렘니스카투스 함수의 유도가 네 번째 거듭제곱함수의 계승자의 제곱근의 역수와 같다는 사실을 보여줍니다.
첫 번째 증명 : 아크탄젠트 도함수와의 비교 오른쪽에 보이는 스케치에는 검은색 대각선이 있습니다. 빨간색 수직 축과 함께 검은색 대각선의 교차점에서 점(10)까지 수직으로 이어지는 세그먼트의 길이를 s라고 해야 합니다. 그리고 좌표 원점에서 이 대각선과 초타원의 청록색 곡선이 교차하는 지점까지의 검은색 대각선 구간의 길이는 slh 값에 따라 다음과 같은 값을 갖습니다.
D ( s ) = ( 1 s 4 + 1 4 ) 2 + ( s s 4 + 1 4 ) 2 = s 2 + 1 s 4 + 1 4 {\displaystyle D(s)={\sqrt {{2}+1}}{\sqrt {1}{\sqrt[{4}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}}{s^{4}+1}}{\biggr )}^{2}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}. 이 연결은 피타고라스 정리 에 의해 설명됩니다.
유사한 단위 원은 설명된 면적 할당과 함께 원 삼각형의 아크탄젠트를 생성합니다.
이에 적용되는 파생상품은 다음과 같습니다.
d d s 아크탄 ( s ) = 1 s 2 + 1 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} s}\arctan(들)={\frac {1}{s^{2}+1}}} 렘니스카투스 쌍곡면의 넓이의 유도를 결정하기 위해, 초타원과 단위 원의 동일한 대각선에 대한 무한히 작은 삼각형 넓이의 비교가 아래에 설정됩니다. 무한히 작은 삼각형 영역의 합이 면적 치수를 설명하기 때문입니다. 사진 속 초타원의 경우 해당 영역의 절반이 녹색으로 표시됩니다. 좌표 원점에서 각도가 무한히 작은 삼각형의 길이에 대한 영역의 2차 비율 때문에 다음 공식이 적용됩니다.
d d s 쓱 ( s ) = [ d d s 아크탄 ( s ) ] D ( s ) 2 = 1 s 2 + 1 D ( s ) 2 = 1 s 2 + 1 ( s 2 + 1 s 4 + 1 4 ) 2 = 1 s 4 + 1 {\displaystyle {\frac {\mathrm {d}}{\mathrm {d}}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d}}{\mathrm {d}}}\arctan(s){\biggr ]}D(s)^{2}}={\frac {1}{s^{2}+1}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}}{\sqrt {s^{4}+1}}^{\biggr )}^{2}={\frac {1}{\sqrt {4}+1}}}} 두 번째 증명: 적분 형성 및 면적 감산 그림에서 면적 접선 렘니스카투스 하이퍼볼리쿠스는 대각선과 곡선의 교차점 높이를 녹색 면적의 두 배로 할당합니다. 녹색 영역 자체는 0에서 해당 높이 값까지의 초타원 함수의 차이 적분에서 인접한 삼각형의 면적을 뺀 값으로 생성됩니다.
아흐로 ( v ) = 2 ( ∫ 0 v 1 − w 4 4 d w ) − v 1 − v 4 4 {\displaystyle {\text{atlh}}(v)=2{\biggl(}\int_{0}^{v}{\sqrt[{4}}}\mathrm {d} w{\biggr}-v{\sqrt[{4}]{1-v^{4}}} d d v 아흐로 ( v ) = 2 1 − v 4 4 − ( d d v v 1 − v 4 4 ) = 1 ( 1 − v 4 ) 3 / 4 {\displaystyle {\frac {\mathrm {d} {\mathrm {d} v}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}-{\biggl(}{\frac {\mathrm {d} v}}{\sqrt[{4}]{1-v^{4}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}} 다음과 같은 변환이 적용됩니다.
쓱 ( x ) = 아흐로 ( x x 4 + 1 4 ) {\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl(}{\frac {x}{\sqrt[{4}]{x^{4}+1}}{\biggr )}} 따라서 연쇄법칙 에 따르면, 이 파생은 다음과 같습니다.
d d x 쓱 ( x ) = d d x 아흐로 ( x x 4 + 1 4 ) = ( d d x x x 4 + 1 4 ) [ 1 − ( x x 4 + 1 4 ) 4 ] − 3 / 4 = {\displaystyle {\frac {\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}{\biggr )}={\biggl (}{\frac {\mathrm {d} x}}{\frac {x}{\sqrt[{4}}{x^{4}+1}}{\biggr )}{\biggl [}}{\frac {x}{x}{\sqrt[4}}{x^{4}+1}}{\biggr )}}{\biggl [}{\frac {x}{x}{\biggr )}^{4}{\biggr ]}^{-3/4}=} = 1 ( x 4 + 1 ) 5 / 4 [ 1 − ( x x 4 + 1 4 ) 4 ] − 3 / 4 = 1 ( x 4 + 1 ) 5 / 4 ( 1 x 4 + 1 ) − 3 / 4 = 1 x 4 + 1 {\displaystyle = {\frac {1}{(x^{4}+1)^{5/4}}{\biggl [}1-{\biggl (}{\frac {x}{x}}{\sqrt[{4}]{x^{4}+1}}}{\biggr ]}^{{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}{\biggl (}}{\frac {1}{x^{4}+1}}^{\biggr )}^{-3/4}={\frac {1}{x^{4}+1}}}}^{\frac {1}}^{\sqrt {x^{4}+1}}}}}. 특정값 다음 목록은 쌍곡선 렘니스케이트 사인 의 값을 정확하게 보여 줍니다.
s l h ( ϖ 2 2 ) = 1 {\displaystyle \mathrm {slh} \,\left ({\frac {\varpi}{2{\sqrt {2}}}\right)=1} s l h ( ϖ 3 2 ) = 1 3 4 2 3 − 3 4 {\displaystyle \mathrm {slh} \,\left ({\frac {\varpi}{3{\sqrt {2}}}\right)={\frac {1}{\sqrt[{4}]{3}}{\sqrt[{4}]{2{\sqrt {3}-3}}} s l h ( 2 ϖ 3 2 ) = 2 3 + 3 4 {\displaystyle \mathrm {slh} \,\left ({\frac {2\varpi}{3{\sqrt {2}}}\right)={\sqrt[{4}}{2{\sqrt {3}}+3}}} s l h ( ϖ 4 2 ) = 1 2 4 ( 2 + 1 − 1 ) {\displaystyle \mathrm {slh} \,\left ({\frac {\varpi}{4{\sqrt {2}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {2}+1}-1)} s l h ( 3 ϖ 4 2 ) = 1 2 4 ( 2 + 1 + 1 ) {\displaystyle \mathrm {slh} \,\left ({\frac {3\varpi}{4{\sqrt {2}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {2}}+1})} s l h ( ϖ 5 2 ) = 1 8 4 5 − 1 20 4 − 5 + 1 = 2 5 − 2 4 죄악의 ( 1 20 π ) 죄악의 ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left ({\frac {\varpi}{5{\sqrt {2}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt{5}-1}}{\sqrt{\sqrt{4}}{20}}}=2{\sqrt{4}{{\sqrt{5}}-2}}{\sqrt{\sqrt{5}-2}}{\sqrt{1}{20}}\pi)\sin({\tfrac{3}{20}}}}}}. s l h ( 2 ϖ 5 2 ) = 1 2 2 4 ( 5 + 1 ) 20 4 − 5 + 1 = 2 5 + 2 4 죄악의 ( 1 20 π ) 죄악의 ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left ({\frac {2\varpi}{5{\sqrt {2}}}\right)={\frac {1}{2{\sqrt[{4}}}}}}{{\sqrt{5}}+1}}}{\sqrt{\sqrt{4}}{-{\sqrt{5}+1}}}=2{\sqrt{5}}+2}}{\sqrt{\sin({\tfrac{1}{20}}\pi)}}}}}}{\sin({\tfrac{3}{20}}\pi}}})}. s l h ( 3 ϖ 5 2 ) = 1 8 4 5 − 1 20 4 + 5 + 1 = 2 5 − 2 4 cos ( 1 20 π ) cos ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left ({\frac {3\varpi}{5{\sqrt {2}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt{5}-1}}{\sqrt{\sqrt{4}}{\sqrt{5}+1}}=2{\sqrt{4}}{\sqrt{5}-2}}{\sqrt{\cos ({\tfrac{1}{20}}\pi)\cos ({\tfrac{3}{20}}\pi}}}}. s l h ( 4 ϖ 5 2 ) = 1 2 2 4 ( 5 + 1 ) 20 4 + 5 + 1 = 2 5 + 2 4 cos ( 1 20 π ) cos ( 3 20 π ) {\displaystyle \mathrm {slh} \,\left ({\frac {4\varpi}{5{\sqrt {2}}}\right)={\frac {1}{2}{{\sqrt {5}}}}{{\sqrt {5}}}}{{\sqrt {4}}{20}}}=2{\sqrt {5}}{\sqrt {2}+2}}{\cos ({\tfrac {1}{20}}\pi )}\cos ({\tfrac {3}{20}}\pi )}}. s l h ( ϖ 6 2 ) = 1 2 ( 2 3 + 3 + 1 ) ( 1 − 2 3 − 3 4 ) {\displaystyle \mathrm {slh} \,\left ({\frac {\varpi}{6{\sqrt {2}}}\right)={\frac {1}{2}}({\sqrt {3}+3})+1)(1-{\sqrt[{4}]{2{\sqrt {3}-3})} s l h ( 5 ϖ 6 2 ) = 1 2 ( 2 3 + 3 + 1 ) ( 1 + 2 3 − 3 4 ) {\displaystyle \mathrm {slh} \,\left ({\frac {5\varpi}{6{\sqrt {2}}}\right)={\frac {1}{2}}({\sqrt {3}}+1)(1+{\sqrt[4}]{2{\sqrt {3}-3})} 다음 표에는 쌍곡선 렘니스케이트 탄젠트 및 코탄젠트 함수의 가장 중요한 값이 나와 있습니다.
z {\displaystyle z} clh z {\displaystyle \operatorname {clh} z} 슬며시쓱 z {\displaystyle \operatorname {slh} z} ctlh z = cos 4 z {\displaystyle \operatorname {ctlh} z=\cos _{4}z} tlh z = 죄악의 4 z {\displaystyle \operatorname {tlh} z=\sin _{4}z} 0 {\displaystyle 0} ∞ {\displaystyle \infty} 0 {\displaystyle 0} 1 {\displaystyle 1} 0 {\displaystyle 0} 1 4 σ {\displaystyle {\tfrac {1}{4}}\sigma } 1 {\displaystyle 1} 1 {\displaystyle 1} 1 / 2 4 {\displaystyle 1{\big /}{\sqrt[{4}]{2}}} 1 / 2 4 {\displaystyle 1{\big /}{\sqrt[{4}]{2}}} 1 2 σ {\displaystyle {\tfrac {1}{2}}\sigma } 0 {\displaystyle 0} ∞ {\displaystyle \infty} 0 {\displaystyle 0} 1 {\displaystyle 1} 3 4 σ {\displaystyle {\tfrac {3}{4}}\sigma } − 1 {\displaystyle -1} − 1 {\displaystyle -1} − 1 / 2 4 {\displaystyle -1{\big /}{\sqrt[{4}]{2}}} 1 / 2 4 {\displaystyle 1{\big /}{\sqrt[{4}]{2}}} σ {\displaystyle \sigma } ∞ {\displaystyle \infty} 0 {\displaystyle 0} − 1 {\displaystyle -1} 0 {\displaystyle 0}
조합 및 반차 정리 쌍곡 Lemniscate Areasine 과 함께 다음 ID를 설정할 수 있습니다.
tlh [ 쓱 ( x ) ] = ctlh [ 패거리 ( x ) ] = x x 4 + 1 4 {\displaystyle {\text{tlh}}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{ aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}. ctlh [ 쓱 ( x ) ] = tlh [ 패거리 ( x ) ] = 1 x 4 + 1 4 {\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}} 쌍곡 렘니스케이트 탄젠트 의 제곱은 tlh {\displaystyle \operatorname {tlh}} ctlh {\displaystyle \operatorname {ctlh}} 쌍곡 렘니스케이트 탄젠트 의 제곱의 피타고라스 대응물입니다.
쌍곡 동축 렘니스카투스의 이등분 정리는 다음과 같습니다.
슬며시쓱 [ 1 2 쓱 ( x ) ] = 2 x x 2 + 1 + x 4 + 1 + x 4 + 1 − x 2 + 1 {\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {\sqrt {x^{2}+1}}{{\sqrt {x^{4}+1}}}}{{\sqrt {x^{4}+1}}}}{\sqrt {x^{2}+1}}}}. 이 공식은 다음 두 공식의 조합으로 밝혀질 수 있습니다.
a s l h ( x ) = 2 호를 [ x ( x 4 + 1 + 1 ) − 1 / 2 ] {\displaystyle \mathrm {aslh}(x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x ({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]} 호를 ( x ) = 2 쓱 ( 2 x 1 + x 2 + 1 − x 2 ) {\displaystyle {\text{arcsl}}(x)={\sqrt {2}\,{\text{aslh}}{\bigl(}{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}{\sqrt {1+x}} }}}+{\sqrt{1-x^{2}}}}{{\bigr}}}. 또한 모든 실수 값 x R {\displaystyle x\in \mathbb {R}} .
슬며시쓱 [ 1 2 패거리 ( x ) ] = x 4 + 1 + x 2 − 2 x x 4 + 1 + x 2 = ( x 4 + 1 − x 2 + 1 ) − 1 / 2 ( x 4 + 1 + 1 − x ) {\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{ aclh}}(x){\bigr ]}={\sqrt {x^{4}+1}}+x^{2}-{\sqrt {x^{4}+1}}+x^{2} }}}={\bigl(}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl(}{\sqrt {x^{4}+1}}-x{\bigr )}} clh [ 1 2 패거리 ( x ) ] = x 4 + 1 + x 2 + 2 x x 4 + 1 + x 2 = ( x 4 + 1 − x 2 + 1 ) − 1 / 2 ( x 4 + 1 + 1 + x ) {\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{ aclh}}(x){\bigr ]}={\sqrt {\sqrt {x^{4}+1}}+x^{2}+{\sqrt {x^{4}+1}}+x^{2} }}}={\bigl(}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr}}^{-1/2}{\bigl(}{\sqrt {x^{4}+1}}+x{\bigr}}} 이들 아이덴티티는 마지막으로 언급한 공식을 따릅니다.
tlh [ 1 2 패거리 ( x ) ] 2 = 1 2 2 − 2 2 x x 4 + 1 − x 2 = ( 2 x 2 + 2 + 2 x 4 + 1 ) − 1 / 2 ( x 4 + 1 + 1 − x ) {\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{ aclh}}(x)] ^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {x^{4}+1}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}}^{\bigl (}{\sqrt {x^{4}+1}}}}}}}{\sqrt {x^{4}+1}}}}-x{\bigr}}}}}:{\sqrt {x^{1}}}: ctlh [ 1 2 패거리 ( x ) ] 2 = 1 2 2 + 2 2 x x 4 + 1 − x 2 = ( 2 x 2 + 2 + 2 x 4 + 1 ) − 1 / 2 ( x 4 + 1 + 1 + x ) {\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{ aclh}}(x)] ^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {x^{4}+1}}}}={\bigl(}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl(}{\sqrt {x^{4}+1}}}+1}}}}}}}{\sqrt {x^{x^{4}}}}+x{\bigr}}}}. 다음과 같은 렘니시틱 사인과 렘니시틱 코사인의 공식은 밀접한 관련이 있습니다.
슬 [ 1 2 2 패거리 ( x ) ] = cl [ 1 2 2 쓱 ( x ) ] = x 4 + 1 − x 2 {\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{ aclh}}(x)] ={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {x^{4}+1}-x^{2}}} 슬 [ 1 2 2 쓱 ( x ) ] = cl [ 1 2 2 패거리 ( x ) ] = x ( x 4 + 1 + 1 ) − 1 / 2 {\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)] ={\text{cl}}[{\tfrac{1}{2}}{\sqrt{2}}\,{\text{ aclh}}(x)] =x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}} 변환 좌표 가우시안 종 곡선 함수에서 부적절한 적분을 결정하는 것과 유사하게 일반적 인 실린더의 좌표 변환을 사용하여 x와 관련하여 적분 f exp x displaystyle (x exp 4}} 다음에서는 두 적분의 증명이 병렬 방식으로 표시됩니다.
가우스 벨 곡선 함수의 원통 좌표 변환 은 다음과 같습니다.
[ ∫ 0 ∞ 익스피드 ( − x 2 ) d x ] 2 = ∫ 0 ∞ ∫ 0 ∞ 익스피드 ( − y 2 − z 2 ) d y d z = {\displaystyle {\biggl [}\int _{0}^{\infty }\exp (-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp (-y^{2}-z^{2}\,\mathrm {d} y\,\mathrm {d} z=} = ∫ 0 π / 2 ∫ 0 ∞ 디트 [ ∂ / ∂ r r cos ( ϕ ) ∂ / ∂ ϕ r cos ( ϕ ) ∂ / ∂ r r 죄악의 ( ϕ ) ∂ / ∂ ϕ r 죄악의 ( ϕ ) ] 익스피드 { − [ r cos ( ϕ ) ] 2 − [ r 죄악의 ( ϕ ) ] 2 } d r d ϕ = {\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty}}\det {\begin{bmatrix}\partial /\partial r\,\r\cos(\phi )&\partial /\partial \phi \,\r\cos(\phi )\\\\\partial r\,\r\sin(\phi )&\partial \phi \,\r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}^{r\sin(\phi ){\bigr \}},\mathrm {\bigr \}},\mathrm {\bigr \} d} r\,\mathrm {d} \phi =} = ∫ 0 π / 2 ∫ 0 ∞ r 익스피드 ( − r 2 ) d r d ϕ = ∫ 0 π / 2 1 2 d ϕ = π 4 {\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty}r\exp (-r^{2})\,\mathrm {d} \phi =\int _{0}^{\pi /2}{\frac {1}{2}}\,\mathrm {d} \phi ={\frac {\pi}{4}} 그리고 이것은 난막증의 경우와 유사한 좌표 변환입니다.
[ ∫ 0 ∞ 익스피드 ( − x 4 ) d x ] 2 = ∫ 0 ∞ ∫ 0 ∞ 익스피드 ( − y 4 − z 4 ) d y d z = {\displaystyle {\biggl [}\int _{0}^{\infty }\exp (-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp (-y^{4}-z^{4}\,\mathrm {d} y\,\mathrm {d} z=} = ∫ 0 ϖ / 2 ∫ 0 ∞ 디트 [ ∂ / ∂ r r ctlh ( ϕ ) ∂ / ∂ ϕ r ctlh ( ϕ ) ∂ / ∂ r r tlh ( ϕ ) ∂ / ∂ ϕ r tlh ( ϕ ) ] 익스피드 { − [ r ctlh ( ϕ ) ] 4 − [ r tlh ( ϕ ) ] 4 } d r d ϕ = {\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}\int _{0}^{\infty}}\det {\text{bmatrix}\partial r\,\r\,{\text{ctlh}(\phi )&\text{ctlh}(\phi )&\text \phi \,\r\,{\text{ctlh}(\phi )\text{tlh}(\phi )&\text{tlh}(\phi )&partial \phi \,\r\,{\text{tlh}}(\phi )\end{bmatrix}\exp {\bigl \{}-{\text{ctlh}(\phi )},{\text{ctlh}}(\phi ){\bi )} igr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d}r\,\mathrm {d} \phi =} = ∫ 0 ϖ / 2 ∫ 0 ∞ r 익스피드 ( − r 4 ) d r d ϕ = ∫ 0 ϖ / 2 π 4 d ϕ = ϖ π 4 2 {\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}\int _{0}^{\infty}r\exp (-r^{4})\,\mathrm {d} \phi =\int _{0}^{\varpi /{\sqrt {2}}{\frac {\sqrt {\pi }}\,\mathrm {d} \phi ={\frac {\varpi {\sqrt {\pi}}{4{\sqrt {2}}}}} 타원적으로 유사한 방정식 체인의 마지막 줄에는 다시 무한소 분석(분석)의 체인 규칙 에 따라 제곱 함수와 통합된 원래의 가우스 벨 곡선이 있습니다.
두 경우 모두 야코비 행렬 의 행렬식은 적분 영역의 원래 함수에 곱해집니다.
통합 영역의 결과적인 새 기능은 새 매개 변수에 따라 통합됩니다.
타원계수와 5차방정식 1858년 찰스 헤르미테 는 전설적인 개혁에서 5원k {\displaystyle k} k' {\ displaystyle '} [68]
θ 5 − 5 2 θ 4 − ( 1 − 4 k 2 k ′ 2 ) 2 2 k 2 k ′ 2 = 0 {\displaystyle {\theta }^{5}-{\frac {5}{2}}^{\theta }^{4}-{\frac {(1-4k^{2}k'^{2})^{2}}{2k^{2}k'^{2}}=0} 2 θ - 5 {\textstyle 2\theta ^{-5}, 1 {\ displaystyle \theta ^{-1}} .
( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 θ − 5 + 5 θ − 1 = 2. {\displaystyle {\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}}\theta ^{-5}+5\theta ^{-1}=2.} 다음으로 선행 계수의 네 번째 루트를 곱하면 다음을 얻을 수 있습니다.
[ ( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 ] 5 4 θ − 5 + 5 [ ( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 ] 1 4 θ − 1 = 2 [ ( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 ] 1 4 {\displaystyle {\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}}{\biggr ]}^{\frac {5}{4}}\theta ^{-5}+5{\biggl [}{\frac {(1-4k^{2}k'^{2}}^{\frac {(1-4k^{2}}}^{\biggr ]}^{\frac {1}{4}}\theta ^{-1}=2{\biggl [}{\frac {(1-4k^{2}k'^{2}}^{k^{2}}^{\biggr ]}^{\frac {1}}^{4}}^{\frac {1}^{4}}^{\frac {1}}^{-1}=2}{\biggl [}}{\frac {(1-4}}}^{. Bring-Jerard 정규 형태 (정도 5, 1, 0의 항만 포함)에서 다항식 x 5 x c {\displaystyle x^{5} 5x 4c
x = [ ( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 ] 1 4 θ − 1 , c = 1 2 [ ( 1 − 4 k 2 k ′ 2 ) 2 k 2 k ′ 2 ] 1 4 {\displaystyle x={\biggl [}{\frac {(1-4k^{2}k'^{2}}^{2}}^{k^{2}}{\biggr ]}^{\frac {1}{4}}\theta ^{-1},\qquad c={\frac {1}{2}}{\biggl [}{\frac {(1-4k^{2}k^{2}}^{2}}^{k^{2}}^{\biggr ]}^{\frac {1}{4}}^{\frac {1}}}^ 타원 모듈러스 k {\displaystyle k} k' {\displaystyle '} 2 k ' 1 {\displaystyle ^{2 k'^{2 c {\displaystyle {\displaystyle '} k {\displaystyle k'}
k = c 4 + 1 + 1 − c 2 c 2 + 2 + 2 c 4 + 1 , k ′ = c 4 + 1 + 1 + c 2 c 2 + 2 + 2 c 4 + 1 . {\displaystyle k={\frac {\sqrt {c^{4}+1}}-c}{\sqrt {2c^{2}+2+2}{\sqrt {c^{4}+1}}},\qquad k'={\sqrt {\sqrt {c^{4}+1}}}{\sqrt {2c^{2}+2}+1}}}}{\sqrt {2c^{4}+1}}}}. 이 두 가지 공식은 쌍곡 렘니세이트 함수의 관점에서 제시될 수 있습니다.
k = tlh [ 1 2 패거리 ( c ) ] 2 , k ′ = ctlh [ 1 2 패거리 ( c ) ] 2 {\displaystyle {\begin{aligned}k&=\operatorname {tlh} {\bigl [}{\tfrac {1}{2}}\operatorname { aclh}(c){\bigr ]}^{2},\k'&=\operatorname {ctlh} {\bigl [}{\tfrac {1}{2}}\operatorname { aclh}(c){\bigr ]}^{2}\end{aligned}} 수론 대수적 수론 에서, 가우스 유리수 Q i ) {\displaystyle \mathbb {Q} (i)} 아벨 확장은 일부 양의 정수 n {\displaystyle n} (i ) {\displaystyle \mathbb {Q} (i,\omega {n})} 필드 입니다. 이것은 원의 분할에 기초한 유리수 {\displaystyle \mathbb {Q}} 크로네커-베버 정리 와 유사합니다. 특히, Q {\displaystyle \mathbb {Q} {\displaystyle n} 대한 n ){\displaystyle \mathbb {Q} (\zeta _{n}) . Hilbert의 12번째 문제 가 된 크로네커의 유겐트라움의 특별한 사례들입니다.
필드 Q i , sl n {\displaystyle \mathbb {Q} (i, \operatorname {sl}(\varpi /n)}( n {\displaystyle n} 경우 ) {\displaystyle x} 및 {\displaystyle y} 타원 곡선 y 2 = x 3 x {\displaystyle ^{2 } = ^{ tors 생성 된 Q( i ){\displaystyle }(i) .
후르비츠 수 베르누이 수 Bn {\ displaystyle \mathrm {B} _{n}}
B n = 절름발이 z → 0 d n d z n z e z − 1 , n ≥ 0 {\displaystyle \mathrm {B} _{n}=\lim _{z\to 0}{\frac {\mathrm {d}^{n}}{\mathrm {d}z^{n}}{\frac {z}{e^{z}-1}},\quad n\geq 0} 에 출연합니다.
∑ k ∈ Z ∖ { 0 } 1 k 2 n = ( − 1 ) n − 1 B 2 n ( 2 π ) 2 n ( 2 n ) ! = 2 ζ ( 2 n ) , n ≥ 1 {\displaystyle \sum _{k\in \mathbb {Z} \setminus \{0\}{\frac {1}{k^{2n}}= (-1)^{n-1}\mathrm {B} _{2n}{\frac {(2\pi)^{2n}}{(2n)! }}=2\zeta(2n),\quad n\geq 1} 여기서 ζ {\displaystyle \zeta} 리만 제타 함수 입니다.
아돌프 후르비츠 의 이름을후르비츠 수 Hn, {\displaystyle \mathrm {H} _{n} 다음과[70] [71]
H n = − 절름발이 z → 0 d n d z n z ζ ( z ; 1 / 4 , 0 ) , n ≥ 0 {\displaystyle \mathrm {H} _{n}=-\lim _{z\to 0}{\frac {\mathrm {d}^{n}}{\mathrm {d} z^{n}}z\zeta (z;1/4,0),\quad n\geq 0} 여기서 ζ ( ; 1 4 , {\displaystyle \zeta (\cdot; 4, 0)} 불변량 4 {\displaystyle 4} 0 {\displaystyle 0} Weierstrass zeta 함수 입니다. 에 등장합니다.
∑ z ∈ Z [ i ] ∖ { 0 } 1 z 4 n = H 4 n ( 2 ϖ ) 4 n ( 4 n ) ! = G 4 n ( i ) , n ≥ 1 {\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4n}}=\mathrm {H} _{4n}{\frac {(2\varpi)^{4n}}{(4n)! }}}=G_{4n}(i),\quad n\geq 1} 여기 Z {\displaystyle \mathbb {Z} [i]} 가우스 정수 이고 G 4 {\ displaystyle G_{4n} 4 n {\displaystyle 4n} 아이젠슈타인 급수 입니다.
∑ n = 1 ∞ n k e 2 π n − 1 = { 1 24 − 1 8 π 한다면 k = 1 B k + 1 2 k + 2 한다면 k ≡ 1 ( m o d 4 ) 그리고. k ≥ 5 B k + 1 2 k + 2 + H k + 1 2 k + 2 ( ϖ π ) k + 1 한다면 k ≡ 3 ( m o d 4 ) 그리고. k ≥ 3. {\displaystyle \displaystyle {\begin{array}{ll}\displaystyle \sum _{n=1}^{\infty}}{\dfrac {n^{k}}{e^{2\pin}-1}}={\begin{case}{\dfrac {1}{8\pi }}\k=1\{\text{if}}\{\dfrac {\mathrm {B} _{k+1}{2k+2}}&{\text{if}}\k\equiv 1\,(\mathrm {mod} \, 4)\{\text{and}}\k\geq 5\{\dfrac {\mathrm {B} _{k+1}}{2k+2}}+{\dfrac {\mathrm {H} _{k+1}}{2k+2}}\left({\dfrac {\varpi}}{\pi}}\right) ^{k+1}&{\text{if}}\k\equiv 3\,(\mathrm {mod} \,4)\{\text{and}}\k\geq 3. \\\\end{case}}\end{array}} H 4 1 10 {\displaystyle \mathrm {H} _{4 1/10
H 4 n = 3 ( 2 n − 3 ) ( 16 n 2 − 1 ) ∑ k = 1 n − 1 ( 4 n 4 k ) ( 4 k − 1 ) ( 4 ( n − k ) − 1 ) H 4 k H 4 ( n − k ) , n ≥ 2 {\displaystyle \mathrm {H} _{4n}={\frac {3}{(2n-3)(16n^{2}-1)}\sum _{k=1}^{n-1}{\binom {4n}{4k}}(4k-1)(4(n-k)-1)\mathrm {H} _{4k}\mathrm {H} _{4(n-k)},\quad n\geq 2} n {\displaystyle n} 4 {\displaystyle 4} Hn 0 {\displaystyle {H} _{n 0 . 이것은 산출합니다[70]
H 8 = 3 10 , H 12 = 567 130 , H 16 = 43 659 170 , … {\displaystyle \mathrm {H} _{8}={\frac {3}{10}},\,\mathrm {H} _{12}={\frac {567}{130}},\,\,\mathrm {H} _{16}={\frac {43\,659}{170},\,\ldots } 또한[73]
교단의 H 4 n = 2 ∏ ( p − 1 ) 4 n p {\displaystyle \operatorname {denom} \mathrm {H} _{4n}=2\prod _{(p-1) 4n}p} 여기서 p p 1 mod {\ displaystyle \ equiv 1\, text{mod}}\,4),} P {\displaystyle p \in \mathbb {P}},
교단의 B 2 n = ∏ ( p − 1 ) 2 n p {\displaystyle \operatorname {denom} \mathrm {B} _{2n}=\prod _{(p-1) 2n}p} 여기서 p {\displaystyle p\in \mathbb {P}} 슈타우트-클라우센 정리 에 의해).
사실, 폰 슈타우트-클라우센 정리는 다음과 같이 말합니다.
B 2 n + ∑ ( p − 1 ) 2 n 1 p ∈ Z , n ≥ 1 {\displaystyle \mathrm {B} _{2n}+\sum _{(p-1) 2n}{\frac {1}{p}}\in \mathbb {Z},\quad n\geq 1} (OEIS 의 수열 A000146 p {\displaystyle p} Z {\displaystyle a\in \mathbb {Z}} 홀수 b Z {\displaystyle b\in \mathbb {Z}} 짝수 {\displaystyle p} p mod 4) {\displaystyle p\equiv \,(\mathrm {mod} \,4 p a 2 b 2 {\displaystyle p = a^{2} b^{2}} 두 제곱의 합에 대한 페르마의 정리 참조)와 b 1 모드 ) displaystyle \equiv +1\,(\mathrm {mod} 4 주어진 displaystyle , a a displaystyle =a_{p}
H 4 n − 1 2 − ∑ ( p − 1 ) 4 n ( 2 a p ) 4 n / ( p − 1 ) p = 데프 G n ∈ Z , n ≥ 1 , {\displaystyle \mathrm {H} _{4n} - {\frac {1}{2}}-\sum _{(p-1) 4n}{\frac {(2a_{p})^{4n/(p-1)}{p}}\mathrl {\overset {\text{def}}{=}\mathrm {G} _{n}\in \mathbb {Z},\quad n\geq 1,} 슬 z = ∑ n = 0 ∞ k 4 n + 1 z 4 n + 1 ( 4 n + 1 ) ! , z < ϖ 2 ⟹ k p ≡ 2 a p ( 모드의 p ) . {\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty}k_{4n+1}{\frac {z^{4n+1}}{(4n+1)! }},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}\implies k_{p}\equiv 2a_{p}\,({\text{mod}}\,p).} 정수 Gn {\ displaystyle \mathrm {G} _{n}} 시퀀스 , -1 , 5 , 253 , displaystyle 0, -1, 253,\ldots .}
n 2 {\displaystyle n\geq } . 4n 1 {\displaystyle 4n+1} Gn 1 (mod) displaystyle {G} _{n}\equiv \,(\mathrm {mod} 4 4n {\displaystyle 4n+1} 아니면 Gn 3 mod ) displaystyle G} _{n equiv \,(\mathrm 4)}.
대신 일부 저자는 H n = H 4 {\displaystyle \mathrm {H} _{n mathrm {H} _{4n}} .
로랑 시리즈의 등장인물 후르비츠 수는 렘니스케이트 함수와 관련된 로랑 급수 확장에서 여러 개 나타납니다.[75]
슬 2 z = ∑ n = 1 ∞ 2 4 n ( 1 − ( − 1 ) n 2 2 n ) H 4 n 4 n z 4 n − 2 ( 4 n − 2 ) ! , z < ϖ 2 슬 ′ z 슬 z = 1 z − ∑ n = 1 ∞ 2 4 n ( 2 − ( − 1 ) n 2 2 n ) H 4 n 4 n z 4 n − 1 ( 4 n − 1 ) ! , z < ϖ 2 1 슬 z = 1 z − ∑ n = 1 ∞ 2 2 n ( ( − 1 ) n 2 − 2 2 n ) H 4 n 4 n z 4 n − 1 ( 4 n − 1 ) ! , z < ϖ 1 슬 2 z = 1 z 2 + ∑ n = 1 ∞ 2 4 n H 4 n 4 n z 4 n − 2 ( 4 n − 2 ) ! , z < ϖ {\displaystyle {\begin{aligned}\operatorname {sl} ^{2}z&=\sum _{n=1}^{\infty}{\frac {2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H} _{4n}}{\frac {z^{4n-2}}{(4n-2)}{\frac {z^{4n-2}}{(4n-2)! }},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}\{\frac {\operatorname {sl}{z}}&={\frac {1}{z}-\sum _{n=1}^{\infty}{\frac {2^{4n}(2-(-1)^{n}^{2n})\mathrm {H} _{4n}}{\frac {z^{4n-1}}{(4n-1)}{(4n-1)}{(4n-1)! }},\quad \left z\right <{\frac {\varpi}{\sqrt {2}}\{\frac {1}{\operatorname {sl} z}}&={\frac {1}{z}}-\sum _{n=1}^{\infty}{\frac {2^{2n}}\mathrm {H}_{4n}}{\frac {z^{4n-1}}{(4n-1)}{(4n-1)}}{(4n-1)! }},\quad \left z\right <\varpi \{\frac {1}{\operatorname {sl}^{2}z}}&={\frac {1}{z^{2}}+\sum _{n=1}^{\infty}}{\frac {2^{4n}}{\frac {4n}}{\frac {z^{4n-2}}{(4n-2}}{(4n-2)}{{(4n-2)}}{\frac {2}! }},\quad \left z\right <\varpi \end{align}}} 마찬가지로 베르누이 수는 다음과 같습니다.
1 죄스러운 2 z = 1 z 2 − ∑ n = 1 ∞ 2 2 n B 2 n 2 n z 2 n − 2 ( 2 n − 2 ) ! , z < π . {\displaystyle {\frac {1}{\sinh ^{2}z}}={\frac {1}{z^{2}}-\sum _{n=1}^{\infty}}{\frac {2^{2n}}{\mathrm {B}{2n}}{\frac {z^{2n-2}}{(2n-2})}{(2n-2)}}{(2n-2)! }},\quad \left z\right <\pi.} Legendre 기호의 사중형 유사체 유사체 p 1 mod 4 {\displaystyle p\equiv 1\,({\text{mod}}\,4)} p {\displaystyle p } . 사분위 잔차 (mod p {\displaystyle }) {\displaystyle a} mod displaystyle p p 4 {\ displaystyle \left({tfrac }{p}\right)_{4} {\displaystyle }( {\displaystyle a} p {\ }) 1 {\displaystyle -1}(
{\displaystyle a} 및 p {\displaystyle p} , p ' i ] {\displaystyle p'\in \mathbb {Z} [i]} [76] 숫자
( a p ) 4 = ∏ p ′ 슬 ( 2 ϖ a p ′ / p ) 슬 ( 2 ϖ p ′ / p ) . {\displaystyle \left ({\frac {a}{p}}\right)_{4}=\prod {p'}{\frac {\operatorname {sl}(2\varpi ap'/p)}{\operatorname {sl}(2\varpi p'/p}}} 이 정리는 다음과 유사합니다.
( a p ) = ∏ n = 1 p − 1 2 죄악의 ( 2 π a n / p ) 죄악의 ( 2 π n / p ) {\displaystyle \left ({\frac {a}{p}}\right)=\prod_{n=1}^{\frac {p-1}{2}}{\frac {\sin(2\pian/p)}{\sin(2\pin/p)}}} 여기서 ( {\displaystyle \left({\tfrac {\cdot}}{\cdot}}\right)} Legendre 기호입니다.
세계지도 투영법 피어스(Peirce, 1879) 의 "퀸시컬 프로젝션에 관한 세계". 1870년대에 미국 해안 조사의 찰스 샌더스 피어스(Charles Sanders Peirce )가 설계한 피어스 퀸시컬 투영 은 입체적으로 투영 된 점들의 역 렘니세이트 사인(복소수로 처리됨)에 기반한 세계 지도 투영 입니다.[77]
쌍곡 렘니스케이트 사인을 통해 복소 평면에 일정한 실제 또는 가상 부분의 선이 투영된 후 구면에 입체적으로 투영되면(리만 구 참조), 결과적인 곡선은 평면 타원 및 하이퍼볼라 의 구면 유사체인 구면 원뿔 입니다.[78] 따라서 렘니세이트 함수(그리고 더 일반적으로 야코비 타원 함수 )는 구형 원뿔에 대한 매개 변수화를 제공합니다.
Lemniscate 함수를 사용하여 지구 에서 정육면체의 6개의 정사각형 면에 대한 등각 지도 투영을 정의할 수도 있습니다.[79] 많은 편미분 방정식 은 등각 매핑을 통해 효과적으로 해결할 수 있기 때문에, 구에서 입방체로의 이 지도는 대기 모델링 에 편리합니다.[80]
참고 항목 메모들 ^ 파냐노 (1718–1723); 오일러 (1761); 가우스 (1917) ^ 가우스(Gauss, 1917) p. 199는 렘니스케이트 사인과 코사인에 각각 sl 과 cl 기호를 사용하였고, 이 표기법은 오늘날 가장 일반적입니다. Cox (1984) p. 316, Eymard & Lafon (2004) p. 204, Lemmermeyer (2000) p. 240.Ayoub (1984) 은 싱글렘 과 코스렘 을 사용합니다.Whittaker & Watson (1920 )은 synemn 과 cosemn 이라는 기호를 사용합니다.어떤 자료들은 일반 문자 Prasolov & Solovyev (1997) 는 렘니스케이트 사인을 φ로 그리고 그것의 도함수를 φ' ^ 원 x 2 y 2 {\displaystyle ^{2} ^{2 }= x } Shurman(2005) 의 정의 에 따라 극방정식 r = θ , {\displaystyle = cos \theta,} 클로버 를 갖는 (12 , 0 ) {\textstyle {\bigl(}, tfrac {1}{2}},0{\bigr}} diameter 원점 중심의 단위- radius 원 x y 2 1 {\displaystyle x^{2} y^{2 1} 아닙니다 . 렘니스케이트 x2 y 2 2 x 2 {\displaystyle {\bigl (}x^{2} y^{2}{\bigr )}{}^{2 x^{2} ^{2}} ^ 기본 주기 (1 i {\displaystyle ( i)\varpi } 1 i ) {\displaystyle (1 )\varpi } ^ Robinson(2019a )은 이 정의에서 시작하여 렘니세이트 함수의 다른 특성을 도출합니다.^ 이 지도는 슈바르츠 (1869 ) 페이지 113 에서 슈바르츠-크리스토펠 지도의 첫 번째 그림이었습니다. ^ 샤파허 (1997). OEIS 시퀀스 A062539 는 렘니스케이트 상수의 십진 숫자를 나열합니다. ^ 레빈 (2006) ^ 토드 (1975) ^ 콕스 (1984) ^ 어두운 영역은 0을 나타내고 밝은 영역은 극을 나타냅니다. sl z {\displaystyle \operatorname {sl} z} 인수 가 - {\displaystyle \pi }(- displaystyle } displaystyle pi} , 2) {\ displaystyle operatorname Arg} \approx 2), 마그네타 (Arg 0 {\displaystyle operatorname {Arg} \approx 0)} , (Ar π 2 {\displaystyle (\operatorname {Arg} \approx \pi /2 (Ar ) {\displaystyle (\operatorname {Arg} \approx )} . ^ 첫 번째 ID와 네 번째 ID를 결합하면 sl z sl z 1 2 {\displaystyle \operatorname {sl} i/\operatorname {sl (1 )\varpi . 이 신원은 (잘못) Eymard & Lafon( 2004) p. 226에 나와 있으며, 오른쪽 앞에 마이너스 표시가 없습니다. ^ 짝수 가우스 정수는 체커보드 의 검은 사각형인 0, 모듈로 1 + i ^ 프라솔로프 & 솔로비예프 (1997); 로빈슨 (2019a) ^ a b 콕스 (2012) ^ Reinhardt & Walker (2010a) § 22.12.6 , § 22.12.12 ^ 마찬가지로 1 sin z n Z 1 n z n {\displaystyle {\frac {1}{\sin sum {n\in \mathbb {Z}{\frac {(-1)^{n}}{z+n\pi}}} ^ Lindqvist & Peetre(2001) 는 이러한 형태 중 첫 번째 형태를 일반화하고 있습니다.^ 아유브 (1984); 프라솔로프 & 솔로비예프 (1997) ^ 오일러 (1761) § 44 페이지 79, § 47 페이지 80–81^ a b 오일러 (1761) §46쪽80쪽 ^ 실제로 i sl β {\displaystyle i^{\varepsilon operatorname {sl {\tfrac {\ \varpi}{2}}. ^ a b c 콕스 앤 하이드 (2014) ^ 고메즈 몰레다 & 라리오 (2019) ^ 최소 양의 주 인수 를 갖는 네 번째 루트가 선택됩니다. ^ 양수 및 홀수 β {\displaystyle 삭제 β O βO {\ displaystyle \operatorname } \Lambda {\ left ({\mathcal {O})/\beta {\mathcal {O})^{\times }\right }. ^ Cox (2013) 페이지 142, 예제 7.29(c)^ 로젠 (1981) ^ 오일러 (1761); 시겔 (1969). Prasolov & Solovyev(1997) 는 렘니스케이트의 극좌표 표현을 사용하여 미분호 길이를 도출하였으나 결과는 같습니다.^ 라인하르트 & 워커 (2010a) §22.18.E6 ^ 시겔 (1969); 샤파허 (1997) ^ 그러한 숫자가 OEIS 시퀀스 A003401 입니다. ^ 아벨 (1827–1828); 로젠 (1981); 프라솔로프 & 솔로비예프 (1997) ^ 오일러 (1786); 스리다란 (2004); Levien (2008) ^ "A104203" . The On-Line Encyclopedia of Integer Sequences .^ Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. pp. 12, 44. ISBN 1-58488-210-7 ^ a b c d "A193543 - Oeis" .^ p. Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. ISBN 1-58488-210-7 ^ p. Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. ISBN 1-58488-210-7 ^ a b "A289695 - Oeis" .^ Wall, H. S. (1948). Analytic Theory of Continued Fractions . Chelsea Publishing Company. pp. 374–375. ^ 라인하르트 & 워커 (2010a) §22.20(ii) ^ 칼슨 (2010) §19.8 ^ Dieckmann, Andreas. "Collection of Infinite Products and Series" . ^ 라인하르트 & 워커 (2010a) § 22.12.12 ; Vigren & Deckmann (2020) p.7^ 일반적으로 sinh ( x n ) {\displaystyle \sinh(x \pi )} sin ( x n i sinh ( x n {\displaystyle \sin(x \pi -i\sinh(ix n\pi )} ^ 라인하르트 & 워커 (2010a) §22.11 ^ 라인하르트 & 워커 (2010a) §22.2.E7 ^ Berndt (1994) 페이지 247, 248, 253^ 라인하르트 & 워커 (2010a) §22.11.E1 ^ Whittaker and Watson (1990) 페이지 469-470 ^ a b Eymard & Lafon (2004) 페이지 227.^ Cartan, H. (1961). Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes (in French). Hermann. p. 160—164. ^ 보타지니 & 그레이 (2013) 페이지 58^ p. 405; 페이지에 오류가 있습니다. φ 17 {\displaystyle \varphi ^{17}} 107 410 154 000 {\tfrac {107}{7\,410\,154\,752\,000}} 107 207 484 56000 {\tfrac {107} \,484\,333\,056\,000} . ^ M {\displaystyle M} M z M 4 ' z M z {\displaystyle M''"'(z) M'(z) M'(z) 3 M z ) 2 2 M ( z ) 2 {\displaystyle +3M" z)^{2} M(z)^{2} 참조 N {\displaystyle N} N z N N' z 2 M 4 0. {\displaystyle (N'') N (z) N' z)^{2} z)^{4 0. ^ M z n 0 1 {\textstyle M(z sum _{n 0}^{\infty}a_{n}z^{n+1}} , {\displaystyle a_{n}} 재발 1 1 1 k 0 n 2 n k 1 a H k 1 n - k 1 )! textstyle a_{n+1 frac {1}{n+1}}\sum k 0}^{n-k+1}a_{\frac {H} n-k+1 1}}{{(n-k+1)}! }}} 0 = 1 {\displaystyle a_{0 = 1} Hn {\displaystyle \mathrm {H} {n} 렘니스케이트 타원 함수 § 후르비츠 수 에 정의된 후르비츠 수이다.^ Zhuravskiy, A. M. (1941). Spravochnik po ellipticheskim funktsiyam (in Russian). Izd. Akad. Nauk. U.S.S.R. ^ 로빈슨 (2019a) ^ ℘ ( z , τ {\displaystyle \wp (z, \ )} 주기 {\displaystyle 1 } ω 2 ω 1 = {\displaystyle \omega _{2}/\omega _ { 1}=\ . ^ Eymard & Lafon (2004) 페이지 234^ Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions . Cambridge University Press. p. 49. ISBN 978-0-521-78563-1 ^ 신원 cl z cn (2 12 {\displaystyle \operatorname {cl} operatorname {cn}}\left sqrt {2}z;{\tfrac {1}{\sqrt {2}}\right)} 그린힐( 1892) 페이지 33 에서 찾을 수 있습니다. ^ http://oeis.org/A175576 ^ p. Berndt, Bruce C. (1989). Ramanujan's Notebooks Part II . Springer. ISBN 978-1-4612-4530-8 ^ 레빈 (2006); 로빈슨 (2019b) ^ 레빈 (2006) 페이지 515^ 헤르미테, 샤를 (1858) "신퀴엠데레의 태양", 콤프테센두스 . 이탈리아어로 번역된 "Sulla risoluzione delle equazioni del quinto grado", p. 258 참조. ^ a b Cox (2012) 페이지 508, 509^ a b c d p. Arakawa, Tsuneo; Ibukiyama, Tomoyoshi; Kaneko, Masanobu (2014). Bernoulli Numbers and Zeta Functions . Springer. ISBN 978-4-431-54918-5 ^ 이와 동등하게, H n = l im z d d n d n 1 2 sl 1 + i z 2 z 2 i displaystyle \mathrm {H } {n}=-\lim {z\to }{\frac {\mathrm {d} ^{n}} \l eft frac {(1+i)z/2}{\operatorname {sl} ((1+i)z/2)}}+{\frac {z}{2}}{\mathcal {E}}\left({\frac {z}{2};i\right ) }, ≥ 4 {\displaystyle n\geq }, E right ( ⋅ i {\displaystyle {\mathcal {E}}(\cdot;i)} i {\displaystyle i} 자코비엡실론 함수 입니다. ^ B2 n 2 n 1 k n 1 2 2 k 2 k B 2 n {\displaystyle \mathrm {B} _{2n frac {1}{2n+1}}\sum {k 1}^{n-1}{\binom {2n}{2k}}\mathrm {B} _{2k} _ 2(n-k )}, {\displaystyle \geq 2} 2 1 / 6{\displaystyle \mathrm {B} {2 1/6}. ^ Katz, Nicholas M. (1975). "The congruences of Clausen — von Staudt and Kummer for Bernoulli-Hurwitz numbers" . Mathematische Annalen . 216 (1): 1–4. ^ p. Hurwitz, Adolf (1963). Mathematische Werke: Band II (in German). Springer Basel AG. ^ Arakawa et al. (2014)는 H4 n {\ displaystyle \mathrm {H} _{4n} 1 sl 2 . {\displaystyle /\operatorname {sl}^{2}} ^ Ogawa, Takuma (2005). "Similarities between the trigonometric function and the lemniscate function from arithmetic view point" . Tsukuba Journal of Mathematics . 29 (1). ^ 피어스 (1879). Guyou(1887) 와 Adams(1925) 는 같은 투영의 가로와 세로의 측면 을 각각 소개했습니다.Lee (1976 )도 참조. 이 저자들은 사각 격자를 가진 자코비 타원 함수의 관점에서 그들의 투영 공식을 씁니다. ^ 아담스 (1925) ^ Adams (1925) ;Lee (1976) .^ 란치치, 퍼서 & 메싱어 (1996); 맥그리거 (2005). 외부 링크 참고문헌 Abel, Niels Henrik (1827–1828) "Recherches sur les fonctions elliptiques" [Research on elliptic functions] (in French). Crelle's Journal Part 1 . 1827. 2 (2): 101–181. doi :10.1515/crll.1827.2.101 .Part 2 . 1828. 3 (3): 160–190. doi :10.1515/crll.1828.3.160 .Adams, Oscar Sherman (1925). Elliptic functions applied to conformal world maps (PDF) . US Government Printing Office. Ayoub, Raymond (1984). "The Lemniscate and Fagnano's Contributions to Elliptic Integrals". Archive for History of Exact Sciences . 29 (2): 131–149. doi :10.1007/BF00348244 .Berndt, Bruce C. (1994). Ramanujan's Notebooks Part IV (First ed.). Springer. ISBN 978-1-4612-6932-8 Bottazzini, Umberto ; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 .Carlson, Billie C. (2010). "19. Elliptic Integrals" . In Olver, Frank ; et al. (eds.). NIST Handbook of Mathematical Functions Cox, David Archibald (January 1984). "The Arithmetic-Geometric Mean of Gauss" . L'Enseignement Mathématique . 30 (2): 275–330.Cox, David Archibald; Shurman, Jerry (2005). "Geometry and number theory on clovers" (PDF) . The American Mathematical Monthly . 112 (8): 682–704. doi :10.1080/00029890.2005.11920241 . Cox, David Archibald (2012). "The Lemniscate". Galois Theory . Wiley. pp. 463–514. doi :10.1002/9781118218457.ch15 . Cox, David Archibald (2013). Primes of the Form x 2 + ny 2 Cox, David Archibald; Hyde, Trevor (2014). "The Galois theory of the lemniscate" (PDF) . Journal of Number Theory . 135 : 43–59. arXiv :1208.2653 doi :10.1016/j.jnt.2013.08.006 . Enneper, Alfred (1890) [1st ed. 1876]. "Note III: Historische Notizen über geometrische Anwendungen elliptischer Integrale." [Historical notes on geometric applications of elliptic integrals]. Elliptische Functionen, Theorie und Geschichte (in German). Nebert. pp. 524–547.Euler, Leonhard (1761). "Observationes de comparatione arcuum curvarum irrectificibilium" [Observations on the comparison of arcs of irrectifiable curves]. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae (in Latin). 6 : 58–84.E252 . (그림 )Euler, Leonhard (1786). "De miris proprietatibus curvae elasticae sub aequatione y = ∫ x x d x / 1 − x 4 {\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}} [On the amazing properties of elastic curves contained in equation y = ∫ x x d x / 1 − x 4 {\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}} Acta Academiae Scientiarum Imperialis Petropolitanae (in Latin). 1782 (2): 34–61. 605 .Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi . Translated by Wilson, Stephen. American Mathematical Society. ISBN 0-8218-3246-8 Fagnano, Giulio Carlo (1718–1723) "Metodo per misurare la lemniscata" [Method for measuring the lemniscate]. Giornale de' letterati d'Italia (in Italian)."Schediasma primo" [Part 1]. 1718. 29 : 258–269."Giunte al primo schediasma" [Addendum to part 1]. 1723. 34 : 197–207."Schediasma secondo" [Part 2]. 1718. 30 : 87–111.Fagnano (1850). "32–34. Metodo per misurare la lemniscata" . Opere Matematiche, vol. 2 . Allerighi e Segati. pp. 293–313. Figures )Gauss, Carl Friedrich (1917). Werke (Band X, Abteilung I) Gómez-Molleda, M. A.; Lario, Joan-C. (2019). "Ruler and Compass Constructions of the Equilateral Triangle and Pentagon in the Lemniscate Curve". The Mathematical Intelligencer . 41 (4): 17–21. doi :10.1007/s00283-019-09892-w . Greenhill, Alfred George (1892). The Applications of Elliptic Functions Guyou, Émile (1887). "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator" [New system of projection of the sphere]. Annales Hydrographiques . Série 2 (in French). 9 : 16–35. Houzel, Christian (1978). "Fonctions elliptiques et intégrales abéliennes" [Elliptic functions and Abelian integrals]. In Dieudonné, Jean (ed.). Abrégé d'histoire des mathématiques, 1700–1900. II (in French). Hermann. pp. 1–113.Hyde, Trevor (2014). "A Wallis product on clovers" (PDF) . The American Mathematical Monthly . 121 (3): 237–243. doi :10.4169/amer.math.monthly.121.03.237 . Kubota, Tomio (1964). "Some arithmetical applications of an elliptic function". Crelle's Journal . 214/215 : 141–145. doi :10.1515/crll.1964.214-215.141 .Langer, Joel C.; Singer, David A. (2010). "Reflections on the Lemniscate of Bernoulli: The Forty-Eight Faces of a Mathematical Gem" (PDF) . Milan Journal of Mathematics . 78 (2): 643–682. doi :10.1007/s00032-010-0124-5 . Langer, Joel C.; Singer, David A. (2011). "The lemniscatic chessboard" . Forum Geometricorum . 11 : 183–199. Lawden, Derek Frank (1989). Elliptic Functions and Applications . Applied Mathematical Sciences. Vol. 80. Springer-Verlag. doi :10.1007/978-1-4757-3980-0 .Lee, Laurence Patrick (1976). Conformal Projections Based on Elliptic Functions Cartographica Monograph. Vol. 16. University of Toronto Press. Lemmermeyer, Franz (2000). Reciprocity Laws: From Euler to Eisenstein . Springer. ISBN 3-540-66957-4 Levien, Raph (2008). The elastica: a mathematical history (PDF) (Technical report). University of California at Berkeley. UCB/EECS-2008-103.Levin, Aaron (2006). "A Geometric Interpretation of an Infinite Product for the Lemniscate Constant". The American Mathematical Monthly . 113 (6): 510–520. doi :10.2307/27641976 . Lindqvist, Peter; Peetre, Jaak (2001). "Two Remarkable Identities, Called Twos, for Inverses to Some Abelian Integrals" (PDF) . The American Mathematical Monthly . 108 (5): 403–410. doi :10.1080/00029890.2001.11919766 . Markushevich, Aleksei Ivanovich (1966). The Remarkable Sine Functions Markushevich, Aleksei Ivanovich (1992). Introduction to the Classical Theory of Abelian Functions . Translations of Mathematical Monographs. Vol. 96. American Mathematical Society. doi :10.1090/mmono/096 . McGregor, John L. (2005). C-CAM: Geometric Aspects and Dynamical Formulation CSIRO Atmospheric Research . 70. McKean, Henry ; Moll, Victor (1999). Elliptic Curves: Function Theory, Geometry, Arithmetic . Cambridge. ISBN 9780521582285 Milne-Thomson, Louis Melville (1964). "16. Jacobian Elliptic Functions and Theta Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions Neuman, Edward (2007). "On Gauss lemniscate functions and lemniscatic mean" (PDF) . Mathematica Pannonica . 18 (1): 77–94.Nishimura, Ryo (2015). "New properties of the lemniscate function and its transformation" . Journal of Mathematical Analysis and Applications . 427 (1): 460–468. doi :10.1016/j.jmaa.2015.02.066 Ogawa, Takuma (2005). "Similarities between the trigonometric function and the lemniscate function from arithmetic view point" . Tsukuba Journal of Mathematics . 29 (1). Peirce, Charles Sanders (1879). "A Quincuncial Projection of the Sphere" . American Journal of Mathematics . 2 (4): 394–397. doi :10.2307/2369491 .Popescu-Pampu, Patrick (2016). What is the Genus? . Lecture Notes in Mathematics. Vol. 2162. Springer. doi :10.1007/978-3-319-42312-8 . Prasolov, Viktor; Solovyev, Yuri (1997). "4. Abel's Theorem on Division of Lemniscate". Elliptic functions and elliptic integrals . Translations of Mathematical Monographs. Vol. 170. American Mathematical Society. doi :10.1090/mmono/170 . Rančić, Miodrag; Purser, R. James; Mesinger, Fedor (1996). "A global shallow-water model using an expanded spherical cube: Gnomonic versus conformal coordinates". Quarterly Journal of the Royal Meteorological Society . 122 (532): 959–982. doi :10.1002/qj.49712253209 . Reinhardt, William P.; Walker, Peter L. (2010a). "22. Jacobian Elliptic Functions" . In Olver, Frank; et al. (eds.). NIST Handbook of Mathematical Functions Reinhardt, William P.; Walker, Peter L. (2010b). "23. Weierstrass Elliptic and Modular Functions" . In Olver, Frank; et al. (eds.). NIST Handbook of Mathematical Functions Robinson, Paul L. (2019a). "The Lemniscatic Functions". arXiv :1902.08614 Robinson, Paul L. (2019b). "The Elliptic Functions in a First-Order System". arXiv :1903.07147 Rosen, Michael (1981). "Abel's Theorem on the Lemniscate". The American Mathematical Monthly . 88 (6): 387–395. doi :10.2307/2321821 .Roy, Ranjan (2017). Elliptic and Modular Functions from Gauss to Dedekind to Hecke . Cambridge University Press. p. 28. ISBN 978-1-107-15938-9 Schappacher, Norbert (1997). "Some milestones of lemniscatomy" (PDF) . In Sertöz, S. (ed.). Algebraic Geometry (Proceedings of Bilkent Summer School, August 7–19, 1995, Ankara, Turkey). Marcel Dekker. pp. 257–290.Schneider, Theodor (1937). "Arithmetische Untersuchungen elliptischer Integrale" [Arithmetic investigations of elliptic integrals]. Mathematische Annalen (in German). 113 (1): 1–13. doi :10.1007/BF01571618 .Schwarz, Hermann Amandus (1869). "Ueber einige Abbildungsaufgaben" [About some mapping problems]. Crelle's Journal (in German). 70 : 105–120. doi :10.1515/crll.1869.70.105 .Siegel, Carl Ludwig (1969). "1. Elliptic Functions". Topics in Complex Function Theory, Vol. I . Wiley-Interscience. pp. 1–89. ISBN 0-471-60844-0 Snape, Jamie (2004). "Bernoulli's Lemniscate" . Applications of Elliptic Functions in Classical and Algebraic Geometry (Thesis). University of Durham. pp. 50–56. Southard, Thomas H. (1964). "18. Weierstrass Elliptic and Related Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions Sridharan, Ramaiyengar (2004) "Physics to Mathematics: from Lintearia to Lemniscate". Resonance . "Part I" . 9 (4): 21–29. doi :10.1007/BF02834853 . "Part II: Gauss and Landen's Work" . 9 (6): 11–20. doi :10.1007/BF02839214 .Todd, John (1975). "The lemniscate constants" . Communications of the ACM . 18 (1): 14–19. doi :10.1145/360569.360580 Vigren, Erik; Dieckmann, Andreas (21 June 2020). "Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges" . Symmetry . 12 (6): 1040. doi :10.3390/sym12061040 Whittaker, Edmund Taylor ; Watson, George Neville (1920) [1st ed. 1902]. "22.8 The lemniscate functions" . A Course of Modern Analysis 
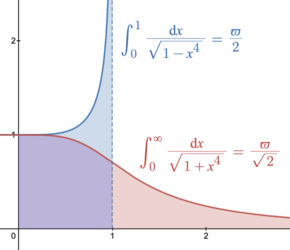
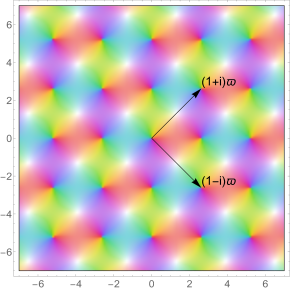
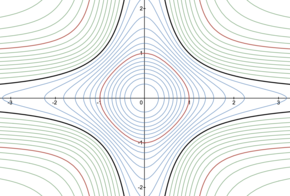



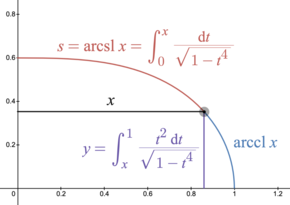
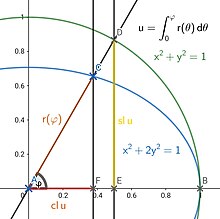


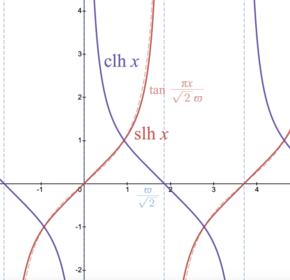

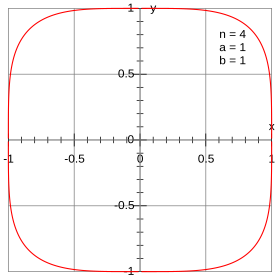












![{\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\[6mu]\operatorname {sl} (-z)&=-\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aad32bc5f3459b050ff3c535a0b2182c24c4410)
![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3960242e95aeb8d86d7c6666d4887c160fbac91c)
![{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+i\varpi )=-\operatorname {cl} z\\[4mu]\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4add8875fadf39f2e07fd34c565655b2e2b236)
![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d7545373f396158c72d1b376d96364cedff009)
![{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cee565bde6b2129ca509f1e6fe214975ad634ae)




 (는) 가우스 정수입니다. 함수
(는) 가우스 정수입니다. 함수![\mathbb {Z} [i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)






 (는) 또 다른 피타고라스와 같은 항등식을 만족합니다
(는) 또 다른 피타고라스와 같은 항등식을 만족합니다

![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-{\bigl (}1+\operatorname {cl^{2}} z{\bigr )}\operatorname {sl} z=-{\frac {2\operatorname {sl} z}{\operatorname {sl} ^{2}z+1}}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&={\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\operatorname {cl} z={\frac {2\operatorname {cl} z}{\operatorname {cl} ^{2}z+1}}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c432d8908a6d28872330b4474cf5c1564bf7cfd)





![{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30e48fbafa5e12f8a952c1f0b8e279f0f9cf5fc)
![{\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v)&=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f19808c18b020503e6fc6074aa10141883d798)
![{\displaystyle {\begin{aligned}\operatorname {cl} (x+iy)&={\frac {\operatorname {cl} x-i\operatorname {sl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y+i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {cl} x\,\operatorname {cl} y\left(1-\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}-i{\frac {\operatorname {sl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\\[12mu]\operatorname {sl} (x+iy)&={\frac {\operatorname {sl} x+i\operatorname {cl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y-i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {sl} x\,\operatorname {cl} y\left(1-\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}+i{\frac {\operatorname {cl} x\,\operatorname {sl} y\left(\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f317fcc9868809494dddb639b23ec4606697f76)










![{\displaystyle \Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta })}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3324adba1f2af9b24673838187cdbe185a69d4b)

![{\displaystyle \Phi _{k}(x)=\prod _{[a]\in (\mathbb {Z} /k\mathbb {Z} )^{\times }}(x-\zeta _{k}^{a}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8960e92721c9f81175d4208b04391e3389bf0fa4)

![{\displaystyle \omega _{5}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6252486e1b91a9d7bdff3ad78a174cb9ea5e19c3)
![{\displaystyle {\tilde {\omega }}_{5}={\sqrt[{4}]{-13-6{\sqrt {5}}+2{\sqrt {85+38{\sqrt {5}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4a18e0684094b21749e757b9054fe4b1bad8d2)

 (가) 소수이고
(가) 소수이고 (가) 양수이고 홀수이면
(가) 양수이고 홀수이면








![{\displaystyle -{\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83cce63fb13a05291d0fb2671c2ab3a62f001fd3)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c74fc1a430f5e7bb0244a281a1d4f1d0647ca67)




![{\displaystyle -{\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce3bc2572b97070b5ca4642620aaa0552dcabf6c)
![{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e7446bf7046ae049852dbd22d5dc78e374b060)





![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b71f8bb130fb48ab5bf0d0cb3dcfd26c827e6a7b)

![{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}-1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52ae25f386dc661dee14e43dd108891a2d9dc43d)
![{\displaystyle {\tfrac {1}{2}}{\sqrt[{4}]{8}}\left[\sin \left({\tfrac {5}{24}}\pi \right)-{\sqrt[{4}]{3}}\sin \left({\tfrac {1}{24}}\pi \right)\right]{\Bigl (}{\sqrt[{4}]{2{\sqrt {3}}+3}}+1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df32229dfa090f41bbafb8ef91fdbc6ff2c5e0f6)

![{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1){\bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9439c6c235f300cf2d5281aace54d0fef0255289)
![{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {3}{20}}\pi )\cos({\tfrac {1}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01c7e40b20b6ca6e6c287c1462d16287e165d056)

![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37780dec3f688806cfed0c5bc96b323e7b4b0799)
![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1084c53e1335a7f8522eeaa4df85eae4f09b949)

![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4e94e7593da5994b86a8d00b41d1a995a271de3)

![{\displaystyle 2\,{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97e7d8ad6ab6e7245cb9d5c25babd2569853dc19)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b34cf55bf836000ca5e342d34a0ec6afea26924)

![{\displaystyle \tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1417b1975f846d4d0b927f839420a78462a5801)









![{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49646481c38b1e3eb1ab582491a98c24fb78c899)


![{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951483e802c58ce9f682e50c2662b425002a37aa)


 원호
원호 



 (는) 다음과 같습니다.
(는) 다음과 같습니다.

 x축 투영이고,
x축 투영이고,
 x축 투영이면, 렘니세이트 타원 함수는 다음과 같이 주어집니다.
x축 투영이면, 렘니세이트 타원 함수는 다음과 같이 주어집니다.


 다음과 같이 결정됩니다.
다음과 같이 결정됩니다.


















































![{\displaystyle {\text{sl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\sin x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\cos ^{2}x}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea0fd8fcd22500f4a1005dc9da044065b9b13891)
![{\displaystyle {\text{cl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\cos x\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh ^{2}[(2n-1)\pi ]-\sin ^{2}x}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b7ebedb88c23dbd7dfa5aa905767ab525b63562)














![{\displaystyle N(z)={\frac {M((1+i)z)}{(1+i)M(z)}},\quad z\notin \varpi \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574d3a65c19e7513f2031d645101f7043784ce55)




 다음과 같이 정의합니다.
다음과 같이 정의합니다.





















![{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb5d4df31aa6a387b048c66646e6f722f3b5f4)
![{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1-\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )}\\[18mu]&{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\[-3mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}={\tan }{\Biggl (}{\frac {\pi }{4}}-{\arctan }{\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a37cc09da1938f7505b12780af4a9d2073a6e404)




![{\displaystyle \operatorname {aslh} (x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4450a96a5aea12b8d6f6c62c03d3069521d772)
![{\displaystyle \operatorname {aclh} (x)=\int _{x}^{\infty }{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\frac {1}{2}}F{\bigl [}2\operatorname {arccot}(x);{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4187488347c3b003b4517d3ff8a364a4a4b5ec39)

![{\displaystyle \operatorname {aslh} (x)={\sqrt {2}}\operatorname {arcsl} {\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e31916e0c226f571375b21b813f8d7698f7384f0)
![{\displaystyle \operatorname {arcsl} (x)={\sqrt {2}}\operatorname {aslh} {\bigl [}x(1+{\sqrt {1-x^{4}}})^{-1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a10b910274a983a4ef695bd0e51357c26e9284a)


![{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f119a40d6612bf47dcb0933374839dd5372e26)





![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d45c585bd9e4ea8c08b7b4a057cec3c98f322bb)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {x}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6942aa471710bbe06a43e659e55a798e1d72023)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{1+{\sqrt {1-x^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45cfc4fa0bf6650e1422d8807eda434011da954)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{{\sqrt {x^{2}+1}}+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dd004729e1ee0cee73ec93ba8f6d70c47fb019e)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d352d10b445bbc88a208fc3d9c759830f8d945)










![{\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56dd44181c73fe6b48af847f7fb236e52b7816a2)
![{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc66d9221d4e85075dc6e4e7eda93fb76745fb63)






![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {slh} (u)^{2}{\bigr ]}=\operatorname {slh} (u)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e51b6288ac0c7a354ecb3c2868e7553a851c8de8)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}-\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {clh} (u)^{2}{\bigr ]}=\operatorname {clh} (u)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/049ec4e8f4e9f40da5061d070f3a5c5d0c662fba)


![{\displaystyle {\text{tlh}}(u)={\frac {{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac149fa68d6fcb0114534181fb5d7e24d78da610)
![{\displaystyle {\text{ctlh}}(u)={\frac {{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a686f87f398e6df8bfc3835f2c39e82473348e0)













![{\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d13d90f0552a5b231cde7c29fcc622ea0c529b6)
![{\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65f62bdd6ed9198c38cf475156efcd304aeb75f9)
![{\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}}=\operatorname {slh} (w)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bb2e7b64a1654bd7915da2f2ee24c36ea102c4d)


![{\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/272cd249cacaf1fb7d3d32aa042602b618e4b78d)

![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adc65177ebceb89021d3d58fb66b072ba8792393)
![{\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cb551ee1709a503d81e9cec4c2b83f7a555bd67)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}}-{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0442203ff4791d46aa1b08d567063c6384a60807)
![{\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a38a1d2985a6df92ef7e4a9e6a5e0769401e0d0)
![{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3366b6e0eca62cd33f2e2e9c7c6e4e34383630c)
![{\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{-3/4}={\frac {1}{\sqrt {x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e4816f6d18a3634e785fa8f89e118ba67ab3465)

![{\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ae714d3e59999777aa261310a9debda59457178)
![{\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt {3}}+3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d46129aba71ca9530722e5d06e4ad3a25cddc8d)
![{\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd287b4155fb6500cce7b0dcce7dafbc62ce24fc)
![{\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb7d14479a3fe31509fddde0687a9c771fc1e0a7)
![{\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b137368ea4f5295289b1ae693dfecfc1c633f9c1)
![{\displaystyle \mathrm {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67f97ed7440315d576356c7c1e42e3fed67fa7f)
![{\displaystyle \mathrm {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/621671dceaa0055339e9e67cb5a0a469dad4fdce)
![{\displaystyle \mathrm {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e7d1a92e821c7f13eba535cd2f4a551440b394e)
![{\displaystyle \mathrm {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1-{\sqrt[{4}]{2{\sqrt {3}}-3}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/959bb353c7095c9df65d73a46093e727ed035f77)
![{\displaystyle \mathrm {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9b7f0ca75d4f5f42f0ce8f5964117096215cd0a)







![{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b95bf2960a1ef78ea3b786b655b45a578835df)


![{\displaystyle -1{\big /}{\sqrt[{4}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a31b674ac78a5a7b3b44666fc5bb8e646d8de17e)

![{\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8332beb95c769a3a02b081fe7cb6952fe061134a)
![{\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e792d8ef543c8092c0ebf91002610e1b870ad46)
![{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2}}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a52e10d08d095a4528b4d3edc8f445388a33fa)
![{\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcbfa061953d1525d7eceb793ec5b9d4ff3d6786)

![{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af856ee0c86e4392d104a519e6a3e4e6dedf2196)
![{\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ed8dda6f6934c99333688d836ecb33384489c9b)
![{\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/526683177df0d4b806ad6ea30226bc7286f39846)
![{\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92f02c5717e1cef246c52819409059208d17659)
![{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b544f5a5f0814402638d89811e6be1e665ca5d3)
![{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]=x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63dce5dab60dff656a75daf045976e8f212d3662)
![{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{2}-z^{2})\,\mathrm {d} y\,\mathrm {d} z=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b51d2740c2198519c7753838241d8bd82ca6b2)
![{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos(\phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d9b620bdfd0a0d029022ce5e0e1cce5781d232c)

![{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{4}-z^{4})\,\mathrm {d} y\,\mathrm {d} z=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0742118348484c98e4d359b6a93ac2843fd6349e)
![{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\,{\text{ctlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{tlh}}(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6a3f5d46d9ca50219760fdf00282b8c3949165)




![{\displaystyle {\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}k'^{2}}}{\biggr ]}^{\frac {5}{4}}\theta ^{-5}+5{\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}k'^{2}}}{\biggr ]}^{\frac {1}{4}}\theta ^{-1}=2{\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}k'^{2}}}{\biggr ]}^{\frac {1}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a269a21c474ca5d6ffe18f3436acb281433f18f6)
![{\displaystyle x={\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}k'^{2}}}{\biggr ]}^{\frac {1}{4}}\theta ^{-1},\qquad c={\frac {1}{2}}{\biggl [}{\frac {(1-4k^{2}k'^{2})^{2}}{k^{2}k'^{2}}}{\biggr ]}^{\frac {1}{4}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6d4d9136af754edddbf28958d86d6b3cbc872e9)

![{\displaystyle {\begin{aligned}k&=\operatorname {tlh} {\bigl [}{\tfrac {1}{2}}\operatorname {aclh} (c){\bigr ]}^{2},\\k'&=\operatorname {ctlh} {\bigl [}{\tfrac {1}{2}}\operatorname {aclh} (c){\bigr ]}^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d6c065ef44b22fd1e1779b429cdfa5320b6e8b4)





![{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4n}}}=\mathrm {H} _{4n}{\frac {(2\varpi )^{4n}}{(4n)!}}=G_{4n}(i),\quad n\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efdff7133fad5cdcaf38afc18fa194e5029ce05a)
 무게
무게 











 사분위수 잔여물(
사분위수 잔여물(
![{\displaystyle p'\in \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3159bf62df44731a1592ff4d718a9b988b83f6ab) 다음과
다음과




