수학함수
수학 에서 야코비 타원 함수 는 기본 타원 함수 의 집합입니다.진자 의 움직임에 대한 설명(진자(수학) 참조)과 전자 타원 필터 의 설계에서 발견됩니다.삼각 함수 는 원을 참조하여 정의되지만, 야코비 타원 함수는 다른 원뿔 단면 , 특히 타원을 참조하는 일반화입니다.삼각 {\displaystyle \sin} sn {\displaystyle \operatorname {sn}} . 자코비 타원 함수는 정의 및/또는 이해하기 위해 복잡한 분석의 개념을 필요로 하지 않기 때문에 Weiersstrass 타원 함수 보다 실제 문제에서 더 자주 사용됩니다. 그것들 은 칼 구스타프 야코프 야코비 (1829 )에 의해 소개되었습니다.칼 프리드리히 가우스 는 이미 1797년에 특수한 야코비 타원 함수, 특히 렘니세이트 타원 함수 를 연구했지만,[1]
개요 u {\displaystyle u} pq ( u , m ) {\displaystyle \operatorname {pq}(u,m)} . p {\displaystyle \mathrm { } } q {\displaystyle \mathrm {q} ) c {\displaystyle \mathrm {c {\displaystyle \mathrm {s}, n {\displaystyle \mathrm {n}, d {\displaystyle \mathrm {d} . pp ( u , m {\displaystyle \operatorname {pp}(u,m)} u {\displaystyle u} m {\displaystyle m} 사실, 야코비 타원 함수는 u {\displaystyle } m {\displaystyle m} 메로포름형 입니다. [2] u {\displaystyle u} 그러나 m {\displaystyle m} [2]
인수 u {\displaystyle u} 극과 영 의 반복 격자를 형성합니다. [3] 함수에 따라 하나의 반복 평행사변형 또는 단위 셀은 실제 축에서 길이2K {\displaystyle 2K} 4K {\displaystyle 4K} 2K' {\ displaystyle 2K' 4K' {\ displaystyle 4K', 여기서 K K m {\displaystyle (m )} K ( 1 m {\displaystyle K ( )} K displaystyle (\cdot )} 타원 적분 인 쿼터 주기 로 알려져 있습니다. 단위 셀의 성질은 원점(0 , displaystyle(0, )} K , K') {\displaystyle(K, K')} 그림에서와 같이 보조 사각형의 네 모서리는 원점에서 시계 반대 방향으로 가는 {\ displaystyle \mathrm {s {\ displaystyle \mathrm {c d {\ displaystyle \mathrm {d}, {\ displaystyle \mathrm {n}} 함수 pq ( u , ) {\displaystyle \operatorname {pq}(u,m)} p {\displaystyle \mathrm {p}} q {\displaystyle \mathrm {q} 12개의 함수는 직사각형의 모서리에 이러한 극과 영을 배열하는 12개의 방법에 해당합니다.
인수 u {\displaystyle u} 매개 {\displaystyle m} 0 1 {\displaystyle 0 m 1} K {\displaystyle K} K' {\ displaystyle K'}
야코비안 타원 함수는 u {\displaystyle u} 토러스 를 통해 인수분해합니다. 사실상 코사인과 사인이 원에 정의된 것처럼 도메인이 토러스가 될 수 있습니다. 원을 하나만 가지는 대신, 이제 우리는 두 개의 원의 곱을 가지게 되었습니다. 하나는 실수이고 다른 하나는 허수입니다. 복잡한 평면은 복잡한 토러스 로 대체될 수 있습니다. 첫 번째 원의 원둘레는 4K {\displaystyle 4K} 4K' {\ displaystyle 4K' . K {\displaystyle K} K {\ displaystyle '} 주기 입니다 각 함수에는 토러스의 반대 위치에 0과 극이 두 개 있습니다. 점 0 {\displaystyle 0}, {\displaystyle K K K' {\ displaystyle K+iK'}, i K' {\ displaystyle iK'}
자코비안 타원 함수는 다음 성질을 만족시키는 이중 주기, 형형 함수입니다.
모서리 displaystyle mathrm }} , q {\ displaystyle \mathrm {q}} . 복소수 p q {\displaystyle \mathrm {p} \mathrm {q}} ( pq u {\displaystyle \operatorname {pq} u} pq {\displaystyle \operatorname {pq} ( pq {\displaystyle \operatorname {pq} . 주기가 2( p q {\displaystyle 2(\mathrm {p} \mathrm {q} ) . 함수 pq u {\displaystyle \operatorname {pq} u} 다른 pp {\ displaystyle \mathrm {pp}' pq {\displaystyle \mathrm {p}' p-q {\ displaystyle mathrm }' p-q' displaystyle mathrm p} \mathrm {q}' . 야코비 타원 함수 sn {\displaystyle operatorname {sn}} 자코비 타원 함수 cn {\displaystyle \operator {cn}} Jacobi 타원 함수 dn {\displaystyle \operatorname {dn}} Jacobi 타원 함수 sc {\displaystyle \operatorname {sc}} u {\displaystyle u} 도메인 컬러링 방법의 버전을 사용하여 생성된 이미지.[4] 모두 {\displaystyle sqrt }} 8 {\displaystyle 0.8} .
표기법 타원 함수는 다양한 표기법으로 주어질 수 있으며, 이는 주제를 불필요하게 혼란스럽게 만들 수 있습니다. 타원 함수는 두 변수의 함수입니다. 첫 번째 변수는 진폭 φ {\displaystyle \varphi} , 주어진 displaystyle } 두 번째 변수는 매개 변수 m {\displaystyle m} 타원 모듈러스 {\displaystyle }( k2 m {\displaystyle ^{2 m 모듈 각도 {\displaystyle \alpha m sin 2 {\displaystyle sin ^{2}\alpha }) . k {\displaystyle k} {\displaystyle m} m' 1 displaystyle 1-m} k' m' {\textstyle sqrt {m'} . 이 네 가지 용어는 다양한 표현을 단순화하기 위해 주석 없이 아래에 사용됩니다.
12개의 자코비 타원 함수는 일반적으로 pq ( u , m ) {\displaystyle \operatorname {pq} (u,m)} p {\displaystyle \mathrm {p} } q {\displaystyle \mathrm {c}, {\displaystyle \mathrm {s}, n {\displaystyle \mathrm {n}, d {\displaystyle \mathrm {d} 하나 . pp ( u , m ) {\displaystyle \operatorname {pp}(u,m)} "주요" 함수는 일반적으로 cn u , m ) {\displaystyle \operatorname {cn} (u,m sn u , m ) {\displaystyle \operatorname {sn} (u,m) dn ( u , m ) {\displaystyle \operatorname {dn} (u,m)} ver, 다양한 대칭과 일반화는 종종 전체 집합을 사용하여 가장 편리하게 표현됩니다. (이 표기법은 Gudermann 과 Glaisher 때문이며, Jacobi의 원래 표기법이 아닙니다.)
이 글 전체에서 pq u , t2 )pq u ; t {\displaystyle \operatorname {pq} (u,t^{2}) \operatorname pq} u;t)}.
함수들은 곱셈 규칙에 의해 서로 연관되어 있지 않습니다: (인수가 억제됨)
p q. ⋅ p ′ q ′ = p q ′ ⋅ p ′ q {\displaystyle \operatorname {pq} \cdot \operatorname {p'q'} =\operatorname {pq'} \cdot \operatorname {p'q} } 일반적으로 사용되는 다른 관계를 도출할 수 있는 방법:
pr qr = p q. {\displaystyle {\frac {\operatorname {pr}}{\operatorname {qr}}}=\operatorname {pq}} pr ⋅ rq = p q. {\displaystyle \operatorname {pr} \cdot \operatorname {rq} =\operatorname {pq}} 1 q p. = p q. {\displaystyle {\frac {1}{\operatorname {qp}}}=\operatorname {pq}} 곱셈 규칙은 타원 함수 를 네빌 세타 함수 로[5]
p q. ( u , m ) = θ p ( u , m ) θ q ( u , m ) {\displaystyle \operatorname {pq}(u,m)={\frac {\theta _{\operatorname {p}}(u,m)}{\theta _{\operatorname {q}}(u,m)}} 참고 사항:
K ( m ) = K ( k 2 ) = ∫ 0 1 d t ( 1 − t 2 ) ( 1 − m t 2 ) = ∫ 0 1 d t ( 1 − t 2 ) ( 1 − k 2 t 2 ) . {\displaystyle K(m)=K(k^{2})=\int _{0}^{1}{\frac {dt}{\sqrt {(1-t^{2})}(1-mt^{2}}}}=\int _{0}^{\frac {dt}{\sqrt {(1-t^{2})}(1-k^{2}}). 타원적분의 역수에 대한 독립변수 u 와 모듈러스 k 의 함수로 자코비 진폭(수직축을 따라 측정) 모형 첫 번째 종류의 불완전한 타원 적분 의 역과 타원 함수를 연관시키는 정의가 있습니다. 이러한 함수는 매개 변수 u {\displaystyle u} m {\displaystyle m} 다음을 만족시키는 φ {\displaystyle \varphi}
u = ∫ 0 φ d θ 1 − m 죄악의 2 θ {\displaystyle u=\int _{0}^{\varphi}{\frac {\mathrm {d} \theta}{\sqrt {1-m\sin ^{2}\theta}}} 자코비 진폭(Jacobi amplitude)이라고 합니다.
암 ( u , m ) = φ . {\displaystyle \operatorname {am}(u,m)=\varphi.} 이 틀에서, 타원 사인 스누 (라틴어: synus amplitudinis )는 다음과 같이 주어집니다.
sn ( u , m ) = 죄악의 암 ( u , m ) {\displaystyle \operatorname {sn}(u,m)=\sin \operatorname {am}(u,m)} 타원 코사인 cnu (라틴어: cosinus amplitudinis )는 다음과 같이 주어집니다.
cn ( u , m ) = cos 암 ( u , m ) {\displaystyle \operatorname {cn}(u,m)=\cos \operatorname {am}(u,m)} 및 델타 진폭 dnu (라틴어: delta amplitudinis )[note 1]
dn ( u , m ) = d d u 암 ( u , m ) . {\displaystyle \operatorname {dn}(u,m)={\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {am}(u,m)} 위에서, 값 m {\displaystyle m} 0 ≤ ≤ 1 {\displaystyle 0\leq m\leq 1} , u {\displaystyle u} m {\displaystyle m} . 나머지 9개의 타원함수는 위의 3개(sn {\displaystyle \operatorname {sn cn {\displaystyle \operatorname {cn}, dn {\displaystyle \operatorname {dn})
가장 일반적인 설정에서 am ( u , m ) {\displaystyle \operatorname {am} (u , m)} ( 2 {\displaystyle 2\pi} 로그 분기점 이 무한히 많은 다중값 함수 (u {\displaystyle 2s K m 4t 1 K 1 i {\displaystyle 2sK m) 4t 1) (1 m ) i} 2s m 4t 3 K 1 i {\displaystyle 2sK(m) 4t 3)K(1-m)i} s, ∈ Z {\displaystyle s, \in \mathbb {Z}}. alueed functions), 따라서 분기 컷 을 제외한 모든 곳에서 am ( u , m ) {\displaystyle \operatorname {am} (u, )} 분석 을 만듭니다. 반대로 sin am ( u , ) {\displaystyle \sin \operatorname {am} u,m)} am {\displaystyle \operatorname {am} 동형 입니다. 모든 타원 함수는 (정의상) 전체 복소 평면에서 형형이기 때문에, am ( u , ) {\displaystyle \operatorname {am} (u,m)}
그러나, 상기 적분 반전은 m {\displaystyle m} u 0 {\displaystyle 0 이웃 에서 고유한 단일 값 실수 analytic 함수를 정의합니다. 이 함수는 그 근방에서 u {\displaystyle u\in \mathbb {R}} 분석적 연속이 있습니다. m displaystyle >1 최소 주기 1 m displaystyle 4K ( m) sqrt }}) 경우 displaystyle a m u , m ) {\displaystyle \operatorname {am}(u,m)}.
자코비는 또한 다음과 같은 경도 함수를 소개했습니다.
c o am u , m = am K m u , {\displaystyle \operatorname {coam} ( u ,m operatorname am K(m)-u,m)}. 자코비엡실론 함수는 다음과[7]
E ( u , m ) = ∫ 0 u dn 2 ( t , m ) d t {\displaystyle {\mathcal {E}}(u,m)=\int_{0}^{u}\operator name {dn}^{2}(t,m)\,\mathrm {d} t} 첫 번째 종류의 불완전한 타원 적분 과 두 번째 종류의 불완전한 타원 적분을 연관시킵니다(매개변수 m {\displaystyle m}
E ( φ , m ) = E ( F ( φ , m ) , m ) . {\displaystyle E(\varphi,m)={\mathcal {E}}(F(\varphi,m),m)} 자코비엡실론 함수는 타원 함수가 아닙니다. 그러나 자코비 진폭 및 동진폭과는 달리 자코비엡실론 함수는 (u {\displaystyle u} m {\displaystyle m}
자코비젠 함수는 다음과 같이 정의됩니다.
zn ( u , m ) = ∫ 0 u ( dn ( t , m ) 2 − E ( m ) K ( m ) ) d t . {\displaystyle \operatorname {zn}(u,m)=\int _{0}^{u}\left(\operatorname {dn}(t,m)^{2}-{\frac {E(m)}{K(m)}\right)\,\mathrm {d} t.} u {\displaystyle u} . 2K ( m ) {\displaystyle 2K(m)} . Z( , ) zn ( F ( , ), m ) 자코비제타 함수 와 관계가 있습니다. {\displaystyle Z(\varphi,m operator {zn}(F(\varphi,m)}
φ = 2{\displaystyle varphi \pi } u {\displaystyle ( ) {\displaystyle .
삼각법으로서의 정의: 야코비 타원 각도 φ 및 매개변수 b 의 특정 값에 대한 야코비 타원(x + y /b = 1, b real) 및 야코비 타원 함수 pq (u ,m )의 그림입니다. 실선 곡선은 m = 1 - 1/b 이고 u = F (φ,m )이며, 여기서 F (··)는 첫 번째 종류의 타원 적분 입니다(모수 m k 2 {\displaystyle ^{2}). 점선 곡선은 단위 원입니다. 원에서 나오는 접선과 dc에서 x축 과 교차하는 x = cd의 타원은 밝은 회색으로 표시됩니다. cos φ , sin φ {\displaystyle \cos \varphi,\sin \varphi } 반지 름 = 각 displaystyle p 마찬가지로, 자코비 타원 함수 는 단위 타원에 a = 1로 정의됩니다.
x 2 + y 2 b 2 = 1 , b > 1 , m = 1 − 1 b 2 , 0 < m < 1 , x = r cos φ , y = r 죄악의 φ {\displaystyle {\begin{aligned}&x^{2}+{\frac {y^{2}}{b^{2}}=1,\quad b>1,\\&m=1-{\frac {1}{b^{2}},\quad 0<m<1,\&x=r\cos \varphi,\quad y=r\sin \varphi \end{aligned}} 다음:
r ( φ , m ) = 1 1 − m 죄악의 2 φ . {\displaystyle r(\varphi,m)={\frac {1}{\sqrt {1-m\sin ^{2}\varphi}},} 각 각도 φ {\displaystyle \varphi}
u = u ( φ , m ) = ∫ 0 φ r ( θ , m ) d θ {\displaystyle u=u(\varphi,m)=\int_{0}^{\varphi }r(\theta,m)\,d\theta } (첫 번째 종류의 불완전한 타원 적분)이 계산됩니다. 단위 원(a b 1 {\displaystyle 1}) {\displaystyle u} 수량 u , k u , k 2 {\displaystyle [\varphi,k u(\varphi,k^{2})} k displaystyle k} )
u [ φ , k ] = 1 1 − k 2 ( 1 + 1 − k 2 2 E ( φ + 아크탄 ( 1 − k 2 태닝한 φ ) , 1 − 1 − k 2 1 + 1 − k 2 ) − E ( φ , k ) + k 2 죄악의 φ cos φ 2 1 − k 2 죄악의 2 φ ) , {\displaystyle u[\varphi,k]={\frac {1}{\sqrt {1-k^{2}}}\left ({\frac {1+{\sqrt {1-k^{2}}}{{2}}\operatorname {E} \left(\varphi +\arctan \left ({\sqrt {1-k^{2}}\tan \varphi \right), {\frac {1-{\sqrt {1-k^{2}}}{{1+{\sqrt {1-k^{2}}}}\right)-\operatorname {E}(\varphi,k)+{\frac {k^{2}\sin \varphi \cos }{2}}}\riefric {1-k^{2}\sqrt {1-k^{2}}}}\rrie ght),} 따라서 타원 의 호 길이 와 관련이 있습니다. P x , y r cos , r sin {\displaystyle x, r \cos \varphi, r\sin \varphi )} P x ',') cos displaystyle y (\cos ,\sin )} 단위 displaystyle {\} 유형 }.
x ′ = cos φ , y ′ = 죄악의 φ {\displaystyle x'=\cos \varphi,\quad y'=\sin \varphi} 타원을 읽습니다.
x ′ = cn ( u , m ) , y ′ = sn ( u , m ) . {\displaystyle x'=\operatorname {cn}(u,m),\quad y'=\operatorname {sn}(u,m)입니다.} 따라서 x축 과 y축의 단위 원을 갖는 O P {\displaystyle OP} P ′{\displaystyle ′} cn ( u , m ) {\displaystyle \operatorname {cn} (u, m ) sn ( u , ) {\displaystyle \operatorname {sn} (u, m) . 간단히 말해서:
cn ( u , m ) = x r ( φ , m ) , sn ( u , m ) = y r ( φ , m ) , dn ( u , m ) = 1 r ( φ , m ) . {\displaystyle \operatorname {cn}(u,m)={\frac {x}{r(\varphi,m)}},\quad \operatorname {sn}(u,m)={\frac {y}{r(\varphi,m)},\quad \operatorname {dn}(u,m)={\frac {1}{r(\varphi,m)}}. u가 {\displaystyle u} m {\displaystyle } {\displaystyle } x {\displaystyle } y {\displaystyle y}
r ( φ , m ) = 1 dn ( u , m ) {\displaystyle r(\varphi,m)={\frac {1}{\operatorname {dn}(u,m)}} 입력: x , cos ), y r , sin {\displaystyle r varphi, cos varphi ), (\varphi, )\sin (\varphi )}:
x = cn ( u , m ) dn ( u , m ) , y = sn ( u , m ) dn ( u , m ) . {\displaystyle x={\frac {\operatorname {cn}(u,m)}{\operatorname {dn}(u,m)}},\quad y={\frac {\operatorname {sn}(u,m)}{\operatorname {dn}(u,m)}} 단위 타원의 점들의 x- 및 y- coordin에 대한 후자의 관계는 단위 원의 점들의 좌표에 대한 x cos , y sin {\displaystyle cos \varphi,y sin \varphi }
다음 표는 변수 x ,y ,r ) 및 (φ,dn)에서 모든 야코비 타원 함수 pq(u,m)에 대한 식을 r = x 2 2 {\textstyle sqrt {x^{2} ^{2}}}
{x ,y ,r } 및 {φ,dn}의 함수로서 야코비 타원 함수 pq[u ,m ] q c s n d p c 1 x / y = 간이 침대 ( φ ) {\displaystyle x/y=\cot(\varphi )} x / r = cos ( φ ) {\displaystyle x/r=\cos(\varphi )} x = cos ( φ ) / dn {\displaystyle x=\cos(\varphi)/\operator name {dn}} s y / x = 태닝한 ( φ ) {\displaystyle y/x=\tan(\varphi )} 1 y / r = 죄악의 ( φ ) {\displaystyle y/r=\sin(\varphi )} y = 죄악의 ( φ ) / dn {\displaystyle y=\sin(\varphi )/\operator name {dn}} n r / x = 초 ( φ ) {\displaystyle r/x=\sec(\varphi )} r / y = csc ( φ ) {\displaystyle r/y=\csc(\varphi )} 1 r = 1 / dn {\displaystyle r=1/\operatorname {dn}} d 1 / x = 초 ( φ ) dn {\displaystyle 1/x=\sec(\varphi )\operator name {dn}} 1 / y = csc ( φ ) dn {\displaystyle 1/y=\csc(\varphi )\operator name {dn}} 1 / r = dn {\displaystyle 1/r=\operatorname {dn}} 1
자코비세타 함수에 대한 정의 자코비테타 함수 설명 동일하게, 야코비의 타원 함수는 그의 세타 함수 로 정의될 수 있습니다. ϑ 00 0 q {\displaystyle vartheta {00}(0;q)} 00 q {\displaystyle vartheta {00}(q)}, 01 ; q ), 11 0 q ) {\displaystyle vartheta {01}( q), \vartheta 10}(0;q), \vartheta 11}(0;q)} 각각 01 q ), 10 q ), 11 q {\ vartheta 01}( \vartheta {\ displaystyle {01 _{10}(q),\vartheta _{11}(q)}( 세타 상수 ) 그러면 세타 함수 타원 모듈러스 k 는 k = { ϑ 10 q ( k ) ϑ 00 q ( k ) } 2 {\displaystyle = biggl \{}{\vartheta _{10}[q(k)] \over \vartheta _{00}[q(k)} biggr \}}^{2 q exp ( π i τ {\displaystyle exp(\pi i \ta )} 우리는 가지고 있다.
sn ( u ; k ) = − ϑ 00 [ q ( k ) ] ϑ 11 [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 10 [ q ( k ) ] ϑ 01 [ u ÷ K ¯ ( k ) ; q ( k ) ] cn ( u ; k ) = ϑ 01 [ q ( k ) ] ϑ 10 [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 10 [ q ( k ) ] ϑ 01 [ u ÷ K ¯ ( k ) ; q ( k ) ] dn ( u ; k ) = ϑ 01 [ q ( k ) ] ϑ 00 [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 00 [ q ( k ) ] ϑ 01 [ u ÷ K ¯ ( k ) ; q ( k ) ] {\displaystyle {\begin{aligned}\operatorname {sn}(u;k)&=-{\farc {\vartheta _{00}[q(k))]\,\vartheta _{11}[u\div {\bar {K}}[q(k)]{\vartheta _{10}[q(k)]\,\vartheta _{01}[u\div {\bar {K}};\,q(k)}}\\[7pt]\operatorname {cn}(u;k)&={\frac {\vartheta _{01}[q(k)]\,\vartheta _{10}[u\div {\bar {K}}(k);\q(k)}{\vartheta _{10}[q(k)]\,\vartheta _{01}[] u\div {\bar {K}}(k);\,q(k)}}\[7pt]\operatorname {dn}(u;k)&={\farc {\vartheta _{01}[q(k)]\,\vartheta _{00}[u\div {\bar {K}}(k);\,q(k)}{\vartheta _{01}[u\div {\bar {K};\,q(k)}}\end{aligned}}} 여기서 K ( k ) 2 K( k ) {\displaystyle {\bar {K}}(k frac {2}{\pi q exp '(k ) K( k )] {\displaystyle exp[-\pi \,K'(k)/K(k)}.
에드먼드 휘태커 (Edmund Whittaker)와 조지 왓슨(George Watson )은 그들의 교과서 Course of Modern Analysis 자코비 세타 함수 를 이렇게 정의했습니다.[9]
ϑ 00 ( v ; w ) = ∏ n = 1 ∞ ( 1 − w 2 n ) [ 1 + 2 cos ( 2 v ) w 2 n − 1 + w 4 n − 2 ] {\displaystyle \vartheta _{00}(v;w)=\prod _{n=1}^{\infty}(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]} ϑ 01 ( v ; w ) = ∏ n = 1 ∞ ( 1 − w 2 n ) [ 1 − 2 cos ( 2 v ) w 2 n − 1 + w 4 n − 2 ] {\displaystyle \vartheta _{01}(v;w)=\prod _{n=1}^{\infty}(1-w^{2n})[1-2\cos(2v)w^{2n-1}+w^{4n-2}]} ϑ 10 ( v ; w ) = 2 w 1 / 4 cos ( v ) ∏ n = 1 ∞ ( 1 − w 2 n ) [ 1 + 2 cos ( 2 v ) w 2 n + w 4 n ] {\displaystyle \vartheta _{10}(v;w)=2w^{1/4}\cos(v)\prod_{n=1}^{\infty}(1-w^{2n})[1+2\cos(2v)w^{2n}+w^{4n}]} ϑ 11 ( v ; w ) = − 2 w 1 / 4 죄악의 ( v ) ∏ n = 1 ∞ ( 1 − w 2 n ) [ 1 − 2 cos ( 2 v ) w 2 n + w 4 n ] {\displaystyle \vartheta _{11}(v;w)=-2w^{1/4}\sin(v)\prod_{n=1}^{\infty}(1-w^{2n})[1-2\cos(2v)w^{2n}+w^{4n}]} 자코비젠 함수 자코비엔 함수는 세타 함수로도 표현할 수 있습니다.
zn ( u ; k ) = π 2 K ϑ 01 ′ [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 01 [ u ÷ K ¯ ( k ) ; q ( k ) ] = π 2 K ϑ 00 ′ [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 00 [ u ÷ K ¯ ( k ) ; q ( k ) ] + k 2 sn ( u ; k ) cn ( u ; k ) dn ( u ; k ) = π 2 K ϑ 10 ′ [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 10 [ u ÷ K ¯ ( k ) ; q ( k ) ] + dn ( u ; k ) sn ( u ; k ) cn ( u ; k ) = π 2 K ϑ 11 ′ [ u ÷ K ¯ ( k ) ; q ( k ) ] ϑ 11 [ u ÷ K ¯ ( k ) ; q ( k ) ] − cn ( u ; k ) dn ( u ; k ) sn ( u ; k ) {\displaystyle {\begin{aligned}\operatorname {zn}(u;k)&={\frac {\pi}{2K}}{\frac {\vartheta _{01}'[u\div {\bar {K}}(k);\,q(k)}{\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)}}\&={\frac {\pi }{2K}}{\frac {\vartheta _{00}'[u\div {\bar {K}}(k);\,q(k)}}{\vartheta _{00}[u\div {\bar {K}}};\,q(k)}}}+k^{2}{\frac {\operatorname {sn}(u;k)}\operatorname {cn}}}{\frac {\vartheta _{00}'[u\div {\bar {K}};\,q(k)}}}}{\frac {\vartheta {00}'[u\div {\bar {k}}}}[u\div {\bar {k}}}}[u\div {,q(k)}}}}}{\frac {\peratorname {sn}(u;k)}}}}{\frac {\frac {\pi}}}}{\farheta {\vartheta {{00}}(u\div {\bar {k}}}}{\k } (u;k)}{\operatorname {dn}(u;k)}}\&={\frac {\pi}{2K}}{\frac {\vartheta _{10}'[u\div {\bar {K}}(k);\,q(k)}{\vartheta _{10}}[u\div {\bar {K}}(k);\,q(k)}}+{\frac {\operatorname {dn}(u;k)}{\operatorname {cn}(u;k)}}\&={\frac {\pi}{2K}}{\farc {11}'[u\div {\bar {K}};\q(k)}{\vartheta _{11}[u\div {\bar {K}}}}{(u\div {\bar {K}}}(k)}}\&v{\frac {\frac {\pi}}{2K}}{\farc {\vartheta _{11}[u\div {\bar {\k}}}(u;k)}{\farcheta _{11}[u\div {\bar {\k}}(u\bar {K}}}(k)}}{\farcheta _{11}[u\div {\bar {\k}}}}(u;k)}}}}{\& {{\frac {\frac {\pi}}}}{\farcheta _{{11}}}[u\far. k);\,q(k)}}-{\frac {\operatorname {cn}(u;k)\operatorname {dn}(u;k)}{\operatorname {sn}(u;k)}}\end{aligned}} 여기서 ' {\ displaystyle'}
ϑ 00 ′ ( v ; w ) = ∂ ∂ v ϑ 00 ( v ; w ) {\displaystyle \vartheta '_{00}(v;w)={\frac {\partial }{\partial v}}\vartheta _{00}(v;w)} ϑ 01 ′ ( v ; w ) = ∂ ∂ v ϑ 01 ( v ; w ) {\displaystyle \vartheta '_{01}(v;w)={\frac {\partial }{\partial v}}\vartheta _{01}(v;w)} 등등.
자코비 지엔 함수의 정의는 다음과 같습니다.
zn ( u ; k ) = ∑ n = 1 ∞ 2 π K ( k ) − 1 죄악의 [ π K ( k ) − 1 u ] q ( k ) 2 n − 1 1 − 2 cos [ π K ( k ) − 1 u ] q ( k ) 2 n − 1 + q ( k ) 4 n − 2 {\displaystyle {\text{zn}}(u;k)=\sum _{n=1}^{\infty}}{\frac {2\pi K(k)^{-1}u]q(k)^{2n-1}}{1-2\cos[\pi K(k)^{-1}u]q(k)^{2n-1}}}} 연속적인 방법으로 진폭 사인을 다음과 같이 생성할 수 있습니다.
sn ( u ; k ) = 2 { zn ( 1 2 u ; k ) + zn [ K ( k ) − 1 2 u ; k ] } k 2 + { zn ( 1 2 u ; k ) + zn [ K ( k ) − 1 2 u ; k ] } 2 {\displaystyle \operatorname {sn}(u;k)={\frac {2}\operatorname {zn}({\tfrac {1}{2}u;k)+\operatorname {zn} [K(k)-{\tfrac {1}{2}u;k]\ }}:{k^{2}+\{\operatorname {zn}({\tfrac {1}{2}u;k)+\operatorname {zn} [K(k)-{\tfrac {1}{2}u;k]\ }^{2}}}} 합과 곱의 비교 제1종 축소 타원 적분은 다음과 같이 다시 정의해야 합니다.
K ¯ ( ε ) = 2 π K ( ε ) {\displaystyle {\bar {K}}(\varepsilon )={\frac {2}{\pi }}K(\varepsilon )} 그리고 축소된 타원형은 다음과 같은 패턴을 따라 정의되어야 합니다.
q ¯ ( ε ) = ε − 2 q ( ε ) 4 {\displaystyle {\bar {q}}(\varepsilon )={\sqrt[{4}]{\varepsilon ^{-2}q(\varepsilon )}}} Peter 와 Jonathan Borwein 형제는 작업 π와 AGM 에서 진폭 사인에 대해 다음과 같은 두 가지 공식을 제공했습니다(60f페이지).
sn ( u ; k ) = 4 K ¯ ( k ) q ¯ ( k ) 2 죄악의 [ u ÷ K ¯ ( k ) ] ∑ n = 1 ∞ q ( k ) n − 1 [ 1 + q ( k ) 2 n − 1 ] 1 − 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {sn}(u;k)=\,{\frac {4}{{\bar {K}}(k)}\,{\bar {q}}(k)^{2}\sin[u\div {\bar {K}}\sum_{n=1}^{\infty}{\frac {q(k)^{n-1}{\frac {1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)}+q(k)^{4n-2}}}
sn ( u ; k ) = 2 q ¯ ( k ) 죄악의 [ u ÷ K ¯ ( k ) ] ∏ n = 1 ∞ 1 − 2 q ( k ) 2 n cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n 1 − 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {sn}(u;k)=2\,{\bar {q}}(k)\sin[u\div {\bar {K}}(k)]\prod_{n=1}^{\infty}{\frac {1-2q(k)^{2n}\cos[2u\div {\bar {K}}(k)+q(k)^{4n}}\cos[2u\div {\bar {K}}(k)+q(k)^{4n-2}}}
내부 z K {\displaystyle z\rightarrow K(k)-z} .
씨디 ( u ; k ) = 4 K ¯ ( k ) q ¯ ( k ) 2 cos [ u ÷ K ¯ ( k ) ] ∑ n = 1 ∞ q ( k ) n − 1 [ 1 + q ( k ) 2 n − 1 ] 1 + 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {cd}(u;k)=\,{\frac {4}{{\bar {K}}(k)}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}\sum_{n=1}^{\infty}{\frac {q(k)^{n-1}{\frac {1+q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)}+q(k)^{4n-2}}}
씨디 ( u ; k ) = 2 q ¯ ( k ) cos [ u ÷ K ¯ ( k ) ] ∏ n = 1 ∞ 1 + 2 q ( k ) 2 n cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n 1 + 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {cd}(u;k)=2\,{\bar {q}}(k)\cos[u\div {\bar {K}}(k)]\prod_{n=1}^{\infty}{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}(k)}+q(k)^{4n}}\cos[2u\div {\bar {\k}(k)}+q(k)^{4n-2}}}
이러한 공식은 Whittaker와 Watson의 0이 아닌 세타 값 함수 에 대한 정의를 기반으로 합니다.
다음 공식은[10]
cn ( u ; k ) = 4 K ¯ ( k ) q ¯ ( k ) 2 cos [ u ÷ K ¯ ( k ) ] ∑ n = 1 ∞ ( − 1 ) n + 1 q ( k ) n − 1 [ 1 − q ( k ) 2 n − 1 ] 1 − 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {cn}(u;k)=\,{\frac {4}{{\bar {K}}(k)}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}\sum_{n=1}^{\infty}{\frac {(-1)^{n+1}q(k)^{n-1}[1-q(k)^{2n-1}}\cos[2u\div {\bar {K}}+q(k)^{4n-2}}}
cn ( u ; k ) = 2 1 − k 2 4 q ¯ ( k ) cos [ u ÷ K ¯ ( k ) ] ∏ n = 1 ∞ 1 + 2 q ( k ) 2 n cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n 1 − 2 q ( k ) 2 n − 1 cos [ 2 u ÷ K ¯ ( k ) ] + q ( k ) 4 n − 2 {\displaystyle \operatorname {cn}(u;k)=2\,{\sqrt[{4}]{1-k^{2}}\,{\bar {q}}(k)\cos[u\div {\bar {K}}}\prod_{n=1}^{\infty}{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}}(k)}+q(k)^{4n}}\cos[2u\div {\bar {K}}(k)}+q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)}+q(k)^{4n-2}}}}
Whittaker-Watson 제품 공식에 따르면, 이 공식은 델타 진폭 함수에도 적용됩니다.
dn ( u ; k ) = 1 − k 2 4 ∏ n = 1 ∞ 1 + 2 cos [ 2 u ÷ K ¯ ( k ) ] q ( k ) 2 n − 1 + q ( k ) 4 n − 2 1 − 2 cos [ 2 u ÷ K ¯ ( k ) ] q ( k ) 2 n − 1 + q ( k ) 4 n − 2 {\displaystyle \operatorname {dn}(u;k)={\sqrt[{4}]{1-k^{2}}\prod_{n=1}^{\infty}}{\frac {1+2\cos[2u\div {\bar {K}}(k)^{2n-1}+q(k)^{4n-2}}{1-2\cos[2u\div {\bar {K}}(k)^{2n-1}+q(k)^{4n-2}}}}}. 쌍곡선 시맨트 합 을 사용하면 델타 진폭에 대해 가능한[11]
dn ( z ; k ) = π 2 K ( 1 − k 2 ) ∑ n = − ∞ ∞ 뒤지다 { π K ( 1 − k 2 ) − 1 [ K ( k ) n + 1 2 z ] } {\displaystyle \operatorname {dn}(z;k)={\frac {\pi}{2K({\sqrt {1-k^{}}}}\sum _{n=-\infty}^{\infty}\operatorname {sech}{\bigl \{}\pi K({\sqrt {1-k^{2}})^{\bigl [}K(k)n+{\tfrac {1}{2}}z{\bigr]}{\bigr \}} 타원형의 명칭과 그 계열 타원적분 및 타원적분 자코비 함수는 타원계수 k( ) {\displaystyle (\ )} , k {\displaystyle k} {\displaystyle . 1 k {\displaystyle sqrt {1-k^{2}}}, 상보계수 로 시작합니다. τ {\displaystyle tau
k ′ ( τ ) = 1 − k 2 = { ϑ 01 [ q ( k ) ] ϑ 00 [ q ( k ) ] } 2 {\displaystyle k'(\tau )={\sqrt {1-k^{2}}={\biggl \{}{\vartheta _{01}[q(k))] \over \vartheta _{00}[q(k)]{\biggr \}^{2}} 첫 번째 종류 의 타원형 과 완전한 타원 적분 을 정의해 보겠습니다.
q ( k ) = 익스피드 [ − π K ( 1 − k 2 ) K ( k ) ] {\displaystyle q(k)=\exp {\biggl [}-\pi {\frac {K({\sqrt {1-k^{2}}})}{K(k)}}{\biggr ]}} 첫 번째 종류의 완전한 타원 적분에 대한 두 가지 동일한 정의는 다음과 같습니다.
K ( k ) = ∫ 0 π / 2 1 1 − k 2 죄악의 ( φ ) 2 ∂ φ {\displaystyle K(k)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin(\varphi )^{2}}}}\partial \varphi } K ( k ) = π 2 ∑ a = 0 ∞ [ ( 2 a ) ! ] 2 16 a ( a ! ) 4 k 2 a {\displaystyle K(k)={\frac {\pi}{2}}\sum _{a=0}^{\infty}{\frac {[(2a)!] ^{2}}:{16^{a}(a!) ^{4}}}k^{2a} nome 함수에 대한 동일한 정의는 계열을 사용하여 생성할 수 있습니다. 다음 함수의 ID는 다음과 같습니다.
1 − 1 − k 2 4 1 + 1 − k 2 4 = ϑ 00 [ q ( k ) ] − ϑ 01 [ q ( k ) ] ϑ 00 [ q ( k ) ] + ϑ 01 [ q ( k ) ] = [ ∑ n = 1 ∞ 2 q ( k ) ( 2 n − 1 ) 2 ] [ 1 + ∑ n = 1 ∞ 2 q ( k ) 4 n 2 ] − 1 {\displaystyle {\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}={\frac {\vartheta _{00}[q(k)]-{\vartheta _{01}[q(k)]}{\vartheta _{00}[q(k)]}={\biggl [}\sum _{n=1}^{\infty}}2\,q(k)^{(2n-1)^{2}}}{\biggr ]}{\biggl [}+\sum _{n=1}^{\infty}}2\,q(k)^{4n^{2}}{\biggr]}}{\biggl [} τ {\displaystyle tau } 2 이상 {\ displaystyle } exp ( /2 ) 0 .0658 {\displaystyle exp(-\pi {\sqrt }}/2)\대략 .0658}; 작은 위의 급수는 매우 빠르게 수렴하며, q {\displaystyle q} [12] [13] [14]
q ( k ) = ∑ n = 1 ∞ Sc ( n ) 2 4 n − 3 ( 1 − 1 − k 2 4 1 + 1 − k 2 4 ) 4 n − 3 = k 2 { 1 2 + [ ∑ n = 1 ∞ Sc ( n + 1 ) 2 4 n + 1 k 2 n ] } 4 {\displaystyle q(k)=\sum _{n=1}^{\infty}{\frac {\text{Sc}}(n)}{2^{4n-3}}{\biggl(}{\frac {1-{\sqrt[{4}}{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}{\biggr )}}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {\text{Sc}}{2^{4n+1}}}k^{\biggr ]}{\biggr \}}^{\biggr \}}}^{\biggl \}}{\biggl \}} 다음 표는 Schwarz 정수 시퀀스 A002103의 번호를 정확하게 보여 줍니다.
Sc(1) Sc(2) Sc(3) Sc(4) Sc(5) Sc(6) Sc(7) Sc(8) 1 2 15 150 1707 20910 268616 3567400
크네서 정수열 독일의 수학자 아돌프 크네서는 그의 에세이 Neue Untersuchungeiner Reiheus der elliptischen Funktionen 에서 타원 주기비의 정수열을 연구했고 이 수열의 생성 함수가 타원 함수임을 보여주었습니다. 또한 로버트 프리케(Robert Fricke )라는 이름의 추가 수학자는 그의 에세이 Die elliptischen Funktionen und dihre Anwendungen 에서 이 정수열을 분석하고 이 언급된 순서를 사용하여 정확한 계산 방법을 설명했습니다. 크네서 정수열 Kn(n)은 다음과 같은 방식으로 구성할 수 있습니다.
크나 ( 2 n ) = 2 4 n − 3 ( 4 n 2 n ) + ∑ m = 1 n 4 2 n − 2 m ( 4 n 2 n − 2 m ) 크나 ( m ) {\displaystyle {\text{Kn}}(2n)=2^{4n-3}{\binom {4n}{2n}}+\sum _{m=1}^{n}4^{2n-2m}{\binom {4n}{2n-2m}{\text{Kn}}(m)}
크나 ( 2 n + 1 ) = 2 4 n − 1 ( 4 n + 2 2 n + 1 ) + ∑ m = 1 n 4 2 n − 2 m + 1 ( 4 n + 2 2 n − 2 m + 1 ) 크나 ( m ) {\displaystyle {\text{Kn}}(2n+1)=2^{4n-1}{\binom {4n+2}{2n+1}}+\sum _{m=1}^{n}4^{\binom {4n+2}{2n-2m+1}{\text{Kn}}(m)}
실행 예:
크나 ( 2 ) = 2 × 6 + 1 × 1 = 13 {\displaystyle {\text{Kn}}(2)=2\times 6+1\times {\color {cornflower blue}1}={\color {color {cornflower blue}13}
크나 ( 3 ) = 8 × 20 + 24 × 1 = 184 {\displaystyle {\text{Kn}}(3)=8\times 20+24\times {\color {cornflower blue}1}={\color {color {cornflower blue} 184}
크나 ( 4 ) = 32 × 70 + 448 × 1 + 1 × 13 = 2701 {\displaystyle {\text{Kn}}(4)=32\times 70+448\times {\color {cornflower blue}1}+1\times {\color {color {cornflower blue}13}={\color {color {cornflower blue}2701}
크나 ( 5 ) = 128 × 252 + 7680 × 1 + 40 × 13 = 40456 {\displaystyle {\text{Kn}}(5)=128\times 252+7680\times {\color {cornflower blue}1}+40\times {\color {color {cornflower blue}13}={\color {color {cornflower blue}40456}
크나 ( 6 ) = 512 × 924 + 126720 × 1 + 1056 × 13 + 1 × 184 = 613720 {\displaystyle {\text{Kn}}(6)=512\times 924+126720\times {\color {cornflower blue}1}+1056\times {\color {color {cornflower blue}13}+1\times {\color {color {cornflower blue}613720}
크나 ( 7 ) = 2048 × 3432 + 2050048 × 1 + 23296 × 13 + 56 × 184 = 9391936 {\displaystyle {\text{Kn}}(7)=2048\times 3432+2050048\times {\color {cornflower blue}1}+23296\times {\color {color {cornflower blue}13}+56\times {\color {color {cornflower blue}9391936}
Kneser 시퀀스는 주기 비율(하프 주기 비율)의 Taylor 영상 시리즈에 나타납니다.
1 4 ln ( 16 x 2 ) − π K ′ ( x ) 4 K ( x ) = ∑ n = 1 ∞ 크나 ( n ) 2 4 n − 1 n x 2 n {\displaystyle {\frac {1}{4}}\ln{\bigl(}{\frac {16}{x^{2}}{\bigr )}-{\frac {\pi \,K'(x)}{4\,K(x)}}=\sum _{n=1}^{\infty}{\frac {\text{Kn}(n){2^{4n-1}}\,x^{2n}} 셸바흐 슈바르츠 정수열 수학자 칼 하인리히 셸바흐는 타원형 놈 함수의 맥로린 계열에 나타나는 정수 수열을 발견했습니다. 이 과학자는[15] Die Lehre von den elliptischen Integren und den Thetafunktionen 에서 이 수열 A002103을 상세하게 구성했습니다. 특히 이 작품의 60페이지에는 이 순서의 합성 경로가 그의 작품에 적혀있습니다. 또한 실레시아 독일 수학자 헤르만 아만두스 슈바르츠는 그 의 작품 Formeln und Lehrsäzzzum Gebrauche der elliptischen Funktionen 에서 정수 순서를 54~56페이지 아래로 적었습니다. 이 셸바흐 슈바르츠 수열 Sc(n)(OEIS: A002103)는 20세기의 수학자 카를 테오도르 빌헬름 바이어스트라스 와 루이 멜빌 밀른톰슨 에 의해서도 분석되었습니다. 수학자 아돌프 크네서는 다음과 같은 패턴을 바탕으로 이 수열의 합성 방법을 결정했습니다.
Sc ( n + 1 ) = 2 n ∑ m = 1 n Sc ( m ) 크나 ( n + 1 − m ) {\displaystyle {\text{Sc}}(n+1)={\frac {2}{n}}\sum _{m=1}^{n}{\text{Sc}(m){\text{Kn}}(n+1-m)} 셸바흐 슈바르츠 수열 Sc(n)는 A002103이라는 번호로 온라인 수열 백과사전에 입력되고 크네서 수열 Kn(n)은 A227503이라는 번호로 입력됩니다. 아돌프 크네서는 그의 에세이 Neue Untersuchungeiner Reiheus der elliptischen Funktionen 에서 이 정수열에 대해 연구했고 이 수열의 생성 함수가 타원 함수임을 보여주었습니다. 또한 Robert Fricke 는 그의 에세이 Die elliptischen Funktionen undihre Anwendungen 에서 이 정수열을 분석하고 이를 이용한 정확한 계산 방법을 설명했습니다. 다음 표에는[16] [17]
구성된 수열 크네서와 셸바흐 슈바르츠 색인 n Kn(n)(A227503) Sc(n) (A002103) 1 1 1 2 13 2 3 184 15 4 2701 150 5 40456 1707 6 613720 20910 7 9391936 268616 8 144644749 3567400
다음에서는 셸바흐 슈바르츠 수가 연속적으로 생성되는 방법을 예시로 보여줄 것입니다. 이 경우 Sc(4) = 150, Sc(5) = 1707 및 Sc(6) = 20910이라는 숫자를 가진 예제가 사용됩니다.
S c ( 4 ) = 2 3 ∑ m = 1 3 S c ( m ) K n ( 4 − m ) = 2 3 [ S c ( 1 ) K n ( 3 ) + S c ( 2 ) K n ( 2 ) + S c ( 3 ) K n ( 1 ) ] {\displaystyle \mathrm {Sc}(4)={\frac {2}{3}\sum _{m=1}^{3}\mathrm {Sc}(m)\,\mathrm {Kn}(4-m)={\frac {2}{3}}{\bigl [}{\color {navy}\mathrm {Sc}(1)}\, {\color {cornflowerblue}\mathrm {Sc}(3)}+{\color {navy}\mathrm {Sc}(2)\, {\color {cornflowerblue}\mathrm {Sc}(3)\, {\color {cornflowerblue}\mathrm {Kn}(1)}{\bigr ]} S c ( 4 ) = 2 3 ( 1 × 184 + 2 × 13 + 15 × 1 ) = 150 {\displaystyle {\color {navy}\mathrm {Sc}(4)}={\frac {2}{3}}\bigl(}{\color {navy}1}회 {\color {color {color {color {navy}2}회 {\color {color {color {color {color}13}+{\color {color {navy}15}\color {color {color {color}1}{\bigr}={\color {navy}150}회 {\color {color {color {color}} S c ( 5 ) = 2 4 ∑ m = 1 4 S c ( m ) K n ( 5 − m ) = 2 4 [ S c ( 1 ) K n ( 4 ) + S c ( 2 ) K n ( 3 ) + S c ( 3 ) K n ( 2 ) + S c ( 4 ) K n ( 1 ) ] {\displaystyle \mathrm {Sc}(5)={\frac {2}{4}}\sum _{m=1}^{4}\mathrm {Sc}(m)\,\mathrm {Kn}(5-m)={\frac {2}{4}}{\bigl [}{\color {navy}\mathrm {Sc}(1)}\, {\color {color {cornflowerblue}\mathrm {Sc}(4)+{\color {navy}\mathrm {Sc}(2)\, {\color {cornflowerblue}\mathrm {Sc}(3)+{\color {color {cornflowerblue}(3)\, {\color {cornflowerblue}\mathrm {Kn}(2)}+{\co} lor {navy}\mathrm {Sc}(4)}\,{\color {cornflowerblue}\mathrm {Kn}(1)}{\bigr ]}} S c ( 5 ) = 2 4 ( 1 × 2701 + 2 × 184 + 15 × 13 + 150 × 1 ) = 1707 {\displaystyle {\color {navy}\mathrm {Sc}(5)}={\frac {2}{4}}{\bigl(}{\color {navy}1}회 {\color {color {color {color {color}2701}+{\color {184}2}회 {\color {color {color {color {color {color}15}회 {\color {color {color {color {color {navy}150}\color {color {color {color {color}}{color {color {navy}1707}회 {\color {color {color {color {color}}\color {color {color {color {color}2701}회 \color {color {color {color}15}회 S c ( 6 ) = 2 5 ∑ m = 1 5 S c ( m ) K n ( 6 − m ) = 2 5 [ S c ( 1 ) K n ( 5 ) + S c ( 2 ) K n ( 4 ) + S c ( 3 ) K n ( 3 ) + S c ( 4 ) K n ( 2 ) + S c ( 5 ) K n ( 1 ) ] {\displaystyle \mathrm {Sc}(6)={\frac {2}{5}}\sum _{m=1}^{5}\mathrm {Sc}(m)\,\mathrm {Kn}(6-m)={\frac {2}{5}}{\bigl [}{\color {navy}\mathrm {Sc}(1)}\, {\color {cornflowerblue}\mathrm {Sc}(5)}+{\color {navy}\mathrm {Sc}(2)\, {\color {cornflowerblue}\mathrm {Sc}(4)+{\color {navy}\mathrm {Sc}(3)\,{\color {cornflowerblue}\mathrm {Kn}(3)}+{\co lor {navy}\mathrm {Sc}(4)\,{\color {cornflowerblue}\mathrm {Kn}(2)}+{\color {navy}\mathrm {Sc}(5)}\,{\color {cornflowerblue}\mathrm {Kn}(1)}{\bigr ]} S c ( 6 ) = 2 5 ( 1 × 40456 + 2 × 2701 + 15 × 184 + 150 × 13 + 1707 × 1 ) = 20910 {\displaystyle {\color {navy}\mathrm {Sc}(6)}={\frac {2}{5}}\bigl(}{\color {navy}1}회 {\color {color {color {color}40456}+{\color {navy}2}회 {\color {color {color {color {color}2701}+{\color {navy}15}회 {\color {color {color {color {color}150}\color {color {color {color}13}+{color {navy}1707}\color {color {color {color}1}{\bigr}={\color {color {color} 또는 {navy} 20910}: 그리고 이 순서는 바로 위에 언급된 방식으로 타원형의 맥로린 계열을 만듭니다.
q ( x ) = ∑ n = 1 ∞ Sc ( n ) 2 4 n − 3 ( 1 − 1 − x 2 4 1 + 1 − x 2 4 ) 4 n − 3 = x 2 { 1 2 + [ ∑ n = 1 ∞ Sc ( n + 1 ) 2 4 n + 1 x 2 n ] } 4 {\displaystyle q(x)=\sum _{n=1}^{\infty}{\frac {\text{Sc}}(n){2^{4n-3}}{\biggl(}{\frac {1-{\sqrt[{4}]{1-x^{2}}}}{1+{\sqrt[{4}]{1-x^{2}}}}{\biggr )}}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {\text{Sc}}{2^{4n+1}}^{\biggr ]}{\biggr \}}^{\biggr \}}}^{\biggr \}}}^{\biggl \}}}{\biggl \}} 네빌 세타 함수에 대한 정의 야코비 타원 함수는 네빌 세타 함수 를 사용하여 매우 간단하게 정의할 수 있습니다.[18]
p q. ( u , m ) = θ p ( u , m ) θ q ( u , m ) {\displaystyle \operatorname {pq}(u,m)={\frac {\theta _{\operatorname {p}}(u,m)}{\theta _{\operatorname {q}}(u,m)}} 자코비 타원 함수의 복잡한 곱의 단순화는 종종 이러한 항등식을 사용하여 더 쉽게 됩니다.
자코비 변환 야코비의 상상적 변신 각도 φ의 특정 값에 대한 퇴화 야코비 곡선(x + y /b = 1, b = ∞) 및 12개 야코비 타원 함수 pq(u ,1)의 그림입니다.실선 곡선은 m = 1이고 u = F (φ,1)인 축퇴 타원(x = 1)이며, 여기서 F (·,\middot')는 첫 번째 종류의 타원 적분 입니다. 점선 곡선은 단위 원입니다. 이것들은 m = 0의 자코비 함수들이지만 (circular 삼각 함수들) 허수의 인수들과 함께, 그것들은 6개의 쌍곡 삼각 함수들에 해당합니다. 야코비 가상 변환은 가상 변수 iu 의 다양한 함수 또는 동등하게 m 매개 변수의 다양한 값 사이의 관계를 연관시킵니다. 주요 기능에 관하여:[19] : 506
cn ( u , m ) = nc ( i u , 1 − m ) {\displaystyle \operatorname {cn}(u,m)=\operatorname {nc}(i\,u,1\!-\!m)} sn ( u , m ) = − i sc ( i u , 1 − m ) {\displaystyle \operatorname {sn}(u,m)=-i\operatorname {sc}(i\,u,1\!-\!m)} dn ( u , m ) = dc ( i u , 1 − m ) {\displaystyle \operatorname {dn}(u,m)=\operatorname {dc}(i\,u,1\!-\!m)} 곱셈 규칙을 사용하면 다른 모든 함수를 위의 세 가지로 표현할 수 있습니다. 변환은 일반적으로 pq ( u , m pq pq iu, 1 m {\displaystyle \operatorname {pq} (u,m {\operatorname {pq} '(i\,u,1\!-\!m)} . pq iu, 1 displaystyle _{\operatorname {pq} operatorname pq} '(i\u,1\!-\m)' ecidated pq(u,m). [18] (인수(, 1 m {\displaystyle(i\,u,1\!-\!m)}
Jacobi 가상 변환 γ pq pq ' ( iu, 1 m ) displaystyle \gamma {\operatorname {pq}\operatorname {pq} '(i\,u,1\!-\!m)} q c s n d p c 1 안에 nc nd s -isn 1 -iscc -isd n cn 아이시스 1 씨디 d dn 아이들들 dc 1
쌍곡 삼각함수 는 허수 인수가 있는 원형 삼각함수에 비례하므로, 자코비 함수는 m=1에 대한 쌍곡함수를 산출합니다.그림에서 야코비 곡선은 x = 1과 x = -1에서 두 개의 수직선으로 축퇴되었습니다.
자코비의 실제 변신. 자코비 실수 변환은[5] : 308 함수 에 대한 표현을 산출합니다. 변환은 일반적으로 pq u , pq pq ku, m {\displaystyle \operatorname {pq} (u, displaystyle pq}\operatorname {pq} '(k\, u, 1/m)} . 다음 표는 지정된 pq(u,m )에 대해 γ pq pq ( ku, 1 / m) {\displaystyle \gamma _{\operatorname {pq}}\operatorname {pq} '(k\,u,1/m)} (인수(, 1 / m) {\displaystyle(k\,u,1/m)}
Jacobi 실제 변환 γ pq pq ku, 1 m) {\displaystyle \gamma {\operatorname {pq}}\operatorname {pq} '(k\,u,1/m)} q c s n d p c 1 {\displaystyle 1} k ds {\displaystyle k\operator name {ds}} dn {\displaystyle \operatorname {dn}} dc {\displaystyle \operatorname {dc}} s 1 k sd {\displaystyle {\frac {1}{k}}\operator name {sd} 1 {\displaystyle 1} 1 k sn {\displaystyle {\frac {1}{k}}\operator name {sn} 1 k sc {\displaystyle {\frac {1}{k}}\operator name {sc}} n nd {\displaystyle \operatorname {nd}} k ns {\displaystyle k\operator name {ns}} 1 {\displaystyle 1} nc {\displaystyle \operatorname {nc}} d 씨디 {\displaystyle \operatorname {cd}} k cs {\displaystyle k\operator name {cs}} cn {\displaystyle \operatorname {cn}} 1 {\displaystyle 1}
기타 야코비 변환 자코비의 실제적인 변신과 상상적인 변신은 다양한 방법으로 결합되어 세 가지의 간단한 변신을 더 만들어 낼 수 있습니다.[5] : 214 실수 변환과 허수 변환은 6개의 변환으로 이루어진 그룹(D3 또는 하모닉 그룹 )에서 2개의 변환이다. 만약
μ R ( m ) = 1 / m {\displaystyle \mu _{R}(m)=1/m} 는 실제 변환에서 m 파라미터 에 대한 변환이고,
μ I ( m ) = 1 − m = m ′ {\displaystyle \mu _{I}(m)=1-m=m'} 는 가상 변환 에서 m의 변환이며, 다른 변환들은 이 두 기본 변환들의 연속적인 적용에 의해 구축될 수 있으며, 단지 세 가지 가능성만을 더 산출할 수 있습니다.
μ I R ( m ) = μ I ( μ R ( m ) ) = − m ′ / m μ R I ( m ) = μ R ( μ I ( m ) ) = 1 / m ′ μ R I R ( m ) = μ R ( μ I ( μ R ( m ) ) ) = − m / m ′ {\displaystyle {\begin{aligned}\mu _{IR}(m)&=&\mu _{I}(\mu _{R}(m))&=&-m'/m\mu _{RI}(m)&=&\mu _{R}(\mu _{I}(m)&=&1/m'\mu _{R}(\mu _{I}(\mu _{R}(m)&=&-m/m'\end{aligned}} 이 다섯 가지 변환은 항등식 변환(μ (m ) = m )과 함께 6개의 element 그룹을 산출합니다. 야코비 타원 함수에 관해서, 일반적인 변환은 단지 세 가지 함수를 사용하여 표현될 수 있습니다.
cs ( u , m ) = γ i c s ′ ( γ i u , μ i ( m ) ) {\displaystyle \operatorname {cs}(u,m)=\gamma _{i}\operatorname {cs'}(\gamma _{i}u,\mu _{i}(m))} ns ( u , m ) = γ i n s ′ ( γ i u , μ i ( m ) ) {\displaystyle \operatorname {ns}(u,m)=\gamma _{i}\operatorname {ns'}(\gamma _{i}u,\mu _{i}(m))} ds ( u , m ) = γ i d s ′ ( γ i u , μ i ( m ) ) {\displaystyle \operatorname {ds}(u,m)=\gamma _{i}\operatorname {ds'}(\gamma _{i}u,\mu _{i}(m))} 여기서 i = U, I, IR, R, RI, 또는 RIR로 변환을 식별하고, γ는 이들 세 함수에 공통적인 곱셈 인자이며, prime은 변환 함수를 나타냅니다. 나머지 9개의 변환된 기능은 위의 3개에서 구축할 수 있습니다. 변환을 나타내기 위해 cs, ns, ds 함수를 선택한 이유는 다른 함수들이 이 세 가지의 비율이 되고(역수는 제외) 곱셈 인자가 취소되기 때문입니다.
다음 표에는 세 ps 함수에 대한 곱셈 인자, 변환된 m ' s 및 변환된 6개 변환 각각에 대한 변환된 함수 이름이 나와 있습니다.[5] : 214 (평상시와 같이 k = m, 1 - k = k = m ' 및 인수(γ iu μi ( m )) displaystyle \ _{i} mu _{ m)} )
6가지 변환에 대한 파라미터 변환 i γ i {\displaystyle \gamma_{i} μ i ( m ) {\displaystyle \mu _{i}(m)} cs' ns'의 ds' U 1 m cs ns ds I i m' ns cs ds IR ik −m'/m ds cs ns R k 1/m ds ns cs RI ik1 1/m' ns ds cs RIR k1 −m/m' cs ds ns
따라서 예를 들어, RIR 변환을 위해 다음 표를 작성할 수 있습니다.[18] 변환은 일반적으로 pq u , pq pq ( k' u, -m ') displaystyle pq}(u _ {pq}}\,\operatorname {pq'}(k'\,u,-m/m')}( k' u, -m / m'){\displaystyle (k'\u ,-m/m')}
RIR 변환 γ pq pq q ( k' u, -m / m') {\displaystyle \gamma _{\operatorname {pq}}\,\operatorname {pq'}(k'\,u,-m/m')} q c s n d p c 1 k'cs 씨디 cn s 1k' {\ displaystyle {\frac {1}{k'}} 1 1k' {\ displaystyle {\frac {1}{k'} 1k' {\ displaystyle {\frac {1}{k'}} n dc k ' {\ displaystyle '} 1 dn d nc k ' {\ displaystyle '} nd 1
야코비 변환의 값은 임의의 복소수 매개 변수 m 을 가진 야코비 타원 함수의 집합이 0 ≤ m ≤ 1인 다른 집합으로 변환될 수 있고, u 의 실수 값에 대해서는 함수 값이 실수가 될 것이라는 것입니다.[5] : p. 215
야코비 쌍곡선 각도 φ 및 매개 변수 b 의 특정 값에 대한 야코비 쌍곡선(x + y /b = 1, b 가상 ) 및 야코비 타원 함수 pq(u ,m )의 그림입니다. 실선 곡선은 쌍곡선으로, m = 1 - 1/b 이고 u = F (φ,m )이며, 여기 서 F(···)는 첫 번째 종류의 타원 적분 입니다. 점선 곡선은 단위 원입니다. ds-dc 삼각형의 경우 σ = sin(φ)cos(φ)입니다. 복잡한 수를 소개하면, 우리의 타원은 연관된 쌍곡선을 가지고 있습니다.
x 2 − y 2 b 2 = 1 {\displaystyle x^{2}-{\frac {y^{2}}{b^{2}}=1} 야코비의 가상 변환을[18] x 와 y 에 대한 위의 식의 타원 함수에.
x = 1 dn ( u , 1 − m ) , y = sn ( u , 1 − m ) dn ( u , 1 − m ) {\displaystyle x={\frac {1}{\operatorname {dn}(u,1-m)},\quad y={\frac {\operatorname {sn}(u,1-m)}{\operatorname {dn}(u,1-m)}} 따라서 dn u , m ), y sn u , 1 {\displaystyle operatorname {dn} (u,1-m operatorname {sn} (u,1-m)} . 이로 인해 서론에서 언급한 복잡한 토러스가 발생합니다.[20] 일반적으로 m은 복소수일 수 있지만, m이 실수이고 m<0일 때 곡선은 x 방향의 장축을 갖는 타원입니다. m=0일 때 곡선은 원이고, 0<m<1일 때 곡선은 y 방향의 장축을 갖는 타원입니다. m = 1에서 곡선은 x = ±1에서 두 개의 수직 선으로 퇴화됩니다.form > 1에서 곡선은 쌍곡선입니다.m 이 복잡하지만 실제가 아닌 경우 x 또는 y 또는 둘 다 복잡하며 곡선은 실제 x-y
함수 이름의 두 글자의 순서를 반대로 하면 위의 세 가지 함수의 역수가 됩니다.
ns ( u ) = 1 sn ( u ) , nc ( u ) = 1 cn ( u ) , nd ( u ) = 1 dn ( u ) . {\displaystyle \operatorname {ns}(u)={\frac {1}{\operatorname {sn}(u)},\qquad \operatorname {nc}(u)={\frac {1}{\operatorname {cn}(u)},\qquad \operatorname {nd}(u)={\frac {1}{\operatorname {dn}(u)}}. 마찬가지로 세 기본 함수의 비율은 분자의 첫 글자 다음에 분모의 첫 글자에 해당합니다.
sc ( u ) = sn ( u ) cn ( u ) , sd ( u ) = sn ( u ) dn ( u ) , dc ( u ) = dn ( u ) cn ( u ) , ds ( u ) = dn ( u ) sn ( u ) , cs ( u ) = cn ( u ) sn ( u ) , 씨디 ( u ) = cn ( u ) dn ( u ) . {\displaystyle {\begin{aligned}\operatorname {sc}(u)={\frac {\operatorname {sn}(u)}{\operatorname {cn}(u)}},\qquad \operatorname {sd}(u)={\frac {\operatorname {sn}(u)}{\operatorname {dn}(u)},\qquad \operatorname {dc}(u)={\frac {\operatorname {dn}(u)}{\operatorname {cn}(u)},\qquad \operatorname {ds}(u)={\frac {\operatorname {dn}(u)}{\operatorname {dn}(u)}{\operatorname {dn}(u)}{\operatorname {d}(u)}{\operatorname {d}(u)}}{\operatorname {d}(u)}} eratorname {sn}(u)},\qquad \operatorname {cs}(u)={\frac {\operatorname {cn}(u)}{\operatorname {sn}(u)},\qquad \operatorname {cd}(u)={\frac {\operatorname {cn}(u)}{\operatorname {dn}(u)}}. \end{aligned}} 좀 더 간결하게 말하자면, 우리는
p q. ( u ) = pn ( u ) qn ( u ) {\displaystyle \operatorname {pq}(u)={\frac {\operatorname {pn}(u)}{\operatorname {qn}(u)}}} 여기서 p와 q는 s, c, d 중 하나입니다.
주기성, 극, 잔류물 12개의 자코비 타원 함수 pq(u,m)에 대한 위상 그림을 함수 복소 인수 u로 표시하고 극과 영이 표시됩니다. 그림은 실제 및 가상 방향으로 한 번의 전체 주기 이상이며 오른쪽 하단에 색상 휠에 따라 위상을 나타내는 색상 부분이 표시됩니다(이는 사소한 dd 함수를 대체함). 절대값이 1/3 이하인 영역은 검은색으로 표시되어 대략 0의 위치를 나타내고, 절대값이 3 이상인 영역은 흰색으로 표시되어 대략 극의 위치를 나타냅니다. 모든 그림은 m = 2/3을 사용하고 K = K (m ), K ' = K (1 - m ), K (·)는 첫 번째 종류의 완전한 타원 적분입니다.극의 화살표가 0 위상 방향을 가리킵니다. 오른쪽 화살표와 왼쪽 화살표는 각각 양과 음의 실제 잔여물을 의미합니다. 위쪽 화살표와 아래쪽 화살표는 각각 양과 음의 가상 잔기를 의미합니다. 주장 u 의 복소 평면에서 야코비 타원 함수는 극(및 0)의 반복 패턴을 형성합니다. 극의 잔여물은 부호만 다를 뿐 모두 동일한 절대값을 갖습니다. 각 함수 pq(u ,m )는 극과 영의 위치가 교환되는 "역함수"(곱셈적 의미에서) qp(u ,m )를 갖습니다. 반복되는 주기는 일반적으로 실제 방향과 가상 방향이 다르므로 이를 설명하기 위해 "이중 주기"라는 용어를 사용합니다.
야코비 진폭과 야코비 엡실론 함수는 준주기적입니다.
암 ( u + 2 K , m ) = 암 ( u , m ) + π , {\displaystyle \operatorname {am}(u+2K,m)=\operatorname {am}(u,m)+\pi,} E ( u + 2 K , m ) = E ( u , m ) + 2 E {\displaystyle {\mathcal {E}}(u+2K,m)={\mathcal {E}}(u,m)+2E} 여기서 E( m ) {\displaystyle E(m)} m {\displaystyle m} 번째 종류의 완전한 타원 적분 입니다.
또한.
zn u 2 i K ',m = zn ( u , ) π i K {\displaystyle \operatorname {zn} (u 2iK', operatorname {zn} (u, m {\frac {\pi i} K}}. 야코비 타원함수의 이중주기성은 다음과 같이 나타낼 수 있습니다.
p q. ( u + 2 α K ( m ) + 2 i β K ( 1 − m ) , m ) = ( − 1 ) γ p q. ( u , m ) {\displaystyle \operatorname {pq} (u+2\alpha K(m)+2i\beta K(1-m)\,,,m)= (-1)^{\gamma }\operatorname {pq}(u,m)} 여기서 α 와 β 는 정수의 임의의 쌍입니다. K (·)는 1종류의 완전한 타원 적분으로 4분주기 라고도 합니다. 음의 일치도(γ)는 다음 표에 나와 있습니다.
γ {\displaystyle \gamma } q c s n d p c 0 β α + β α s β 0 α α + β n α + β α 0 β d α α + β β 0
요인(-1)γ 통일성과 같을 때는 완전한 주기성을 표현합니다. 예를 들어, α가 짝수일 때 α만을 포함하는 엔트리에 대해서는 위 식으로 완전 주기성을 나타내고, 함수는 4K(m )와 2iK (1 - m )의 완전 주기를 가짐을 알 수 있습니다. 마찬가지로, β 만을 포함하는 항목이 있는 함수는 2K(m) 및 4iK (1 - m)의 전체 주기를 갖는 반면, α+β를 갖는 함수는 4K(m ) 및 4iK (1 - m )의 전체 주기를 갖습니다.
극과 영의 위치와 함께 위상을 나타내는 각 함수에 대해 하나의 반복 단위를 표시하는 오른쪽 다이어그램에서 다음과 같은 규칙성을 확인할 수 있습니다. 각 함수의 역수는 대각선의 반대이고 크기가 같은 단위 셀이 있고 극과 영이 교환됩니다. (0,0), (K ,0), (0,K ') 및 (K ,K ')에 의해 형성된 보조 직사각형 내의 극 및 영 배치는 상기 서론에서 설명된 극 및 영 배치의 설명에 따른 것인, 방법. 또한 극을 나타내는 흰색 타원의 크기는 해당 극에 대한 잔차의 절대값을 대략적으로 측정한 것입니다. 그림의 원점에 가장 가까운 극의 잔여물(즉, 보조 직사각형에 있음)이 다음 표에 나열되어 있습니다.
자코비 타원함수의 잔기 q c s n d p c 1 − i k {\displaystyle -{\frac {i}{k}} − 1 k {\displaystyle -{\frac {1}{k}} s − 1 k ′ {\displaystyle -{\frac {1}{k'}} 1 k {\displaystyle {\frac {1}{k}} − i k k ′ {\displaystyle -{\frac {i}{k\,k'}} n − 1 k ′ {\displaystyle -{\frac {1}{k'}} 1 − i k ′ {\displaystyle -{\frac {i}{k'}} d -1 1 − i {\displaystyle -i}
해당하는 경우 2K만큼 위로 이동하거나 오른쪽으로 2K'만큼 이동한 극은 값이 같지만 부호가 반대인 반면 대각선으로 반대인 극은 값이 같습니다. 왼쪽 및 아래쪽 가장자리의 극과 영은 단위 셀의 일부로 간주되지만 위쪽 및 오른쪽 가장자리의 극과 영은 그렇지 않습니다.
특수값 렘니시틱 값 모듈러스 k 1 2 2 ( 1 ) {\displaystyle tfrac {1}{2}}{\sqrt { 1)}
적분 K의 3분의 1에 대한 값:
sn [ 1 3 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 ( 12 4 − 3 + 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{2}}{\sqrt {2}}\, {\tfrac {1}{2}}{\sqrt {2}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt[4}]{12}}-{\sqrt {3}+1)} cn [ 2 3 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 ( 3 − 12 4 + 1 ) {\displaystyle \operatorname {cn} {\bigl [}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{,{\sqrt {3}-{\sqrt[4}]{12}+1}} cn [ 1 3 K ( 1 2 2 ) ; 1 2 2 ] = 2 3 − 3 4 {\displaystyle \operatorname {cn} {\bigl [}{\tfrac {1}{2}}{\sqrt {2}}\, ,{\tfrac {1}{2}}{\sqrt {2}\,{\bigr ]}={\sqrt[4}}{2\sqrt {3}-3}} sn [ 2 3 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 ( 27 4 + 3 4 − 2 ) 2 3 − 3 4 {\displaystyle \operatorname {sn} {\bigl[}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr]}={\tfrac {1}{2}}{,{\sqrt[4}]{27}}+{\sqrt[{4}}-{\sqrt{2}}{\sqrt{4}}-{\sqrt{2}}{\sqrt{4}}-{\sqrt{3}-3}}}. 적분 K의 5분의 1 값:
sn [ 1 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 [ 태닝한 ( 1 5 π ) + 1 − 2 태닝한 ( 3 20 π ) ] {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{2}}{\sqrt {2}}\, {\tfrac {1}{2}}{\sqrt {2}\,{\bigr ]}={\tfrac {1}{2}{\bigl [}\pi )+1-{\sqrt {2\tan ({\tfrac {3}{20}\pi )}{\bigr ]}}. sn [ 3 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 [ 태닝한 ( 1 5 π ) − 1 + 2 간이 침대 ( 3 20 π ) ] {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {3}{5}}K({\tfrac {1}{2}}\,{\tfrac {2}},{\sqrt {2}\,{\bigr ]}={\tfrac {1}{2}}{\tfrac {1}{5}\pi)-1+{\sqrt {2\cot ({\tfrac {3}{20}\pi )}{\bigr ]} cn [ 2 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 [ 간이 침대 ( 1 10 π ) − 1 − 2 태닝한 ( 1 20 π ) ] {\displaystyle \operatorname {cn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}\,{\tfrac {2}},{\sqrt {2}\,{\bigr ]}={\tfrac {1}{2}}{\cot ({\tfrac {1}{10}\pi)-1{\sqrt {2\tan ({\tfrac {1}\pi )}{\bigr ]} cn [ 4 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 [ 간이 침대 ( 1 10 π ) + 1 − 2 간이 침대 ( 1 20 π ) ] {\displaystyle \operatorname {cn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}\,{\tfrac {2}},{\sqrt {2}\,{\bigr ]}={\tfrac {1}{2}}{\cot ({\tfrac {1}{10}\pi)+1-{\sqrt {2\cot ({\tfrac {1}\pi)}{\bigr ]} 대응하는 피타고라스의 반대에 대해서는 다음 공식이 유효합니다.
cn [ 1 5 K ( 1 2 2 ) ; 1 2 2 ] = 2 5 − 2 4 죄악의 ( 3 20 π ) cos ( 1 20 π ) {\displaystyle \operatorname {cn} {\bigl[}{\tfrac {1}{2}}\,{\tfrac {2}},{\tfrac {1}{2}},{\sqrt {2}\,{\bigr]}=2{\sqrt{4}}{\sqrt {5}-2},{\sqrt {3}\pi )\cos ({\tfrac {1}{20}\pi )} cn [ 3 5 K ( 1 2 2 ) ; 1 2 2 ] = 2 5 − 2 4 죄악의 ( 1 20 π ) cos ( 3 20 π ) {\displaystyle \operatorname {cn} {\bigl[}{\tfrac {3}{5}}K({\tfrac {1}{2}},{\sqrt {2}},{\bigr]}=2{\sqrt{4}}{\sqrt {5}-2},{\sqrt {1}\pi)\cos ({\tfrac {3}{20}\pi )}} sn [ 2 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 2 태닝한 ( 1 20 π ) 4 ( 간이 침대 ( 1 10 π ) + 1 − 간이 침대 ( 1 10 π ) − 3 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[4}]{2\tan ({\tfrac {1}{20}\pi )},({\sqrt {\cot ({\tfrac {1}{10}\pi )},{\sqrt {\cot ({\tfrac {1}{10}\pi )+1}}-{\sqrt {\cot ({\tfrac {1}\pi )-3}}} sn [ 4 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 2 간이 침대 ( 1 20 π ) 4 ( 간이 침대 ( 1 10 π ) + 3 − 간이 침대 ( 1 10 π ) − 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[4}]{2\cot ({\tfrac {1}{20}\pi )},({\sqrt {\cot ({\tfrac {1}{10}\pi )+3},{\sqrt {\cot ({\tfrac {1}{10}\pi )-{\cot rt\tfrac {1}\pi )-1}} 적분 K의 7분의 1에 대한 값:
cn [ 2 7 K ( 1 2 2 ) ; 1 2 2 ] = 탄 { 1 2 아치형의 [ 1 2 2 죄악의 ( 1 7 π ) 간이 침대 ( 3 28 π ) + 죄악의 ( 1 14 π ) ] } {\displaystyle \operatorname {cn} [{\tfrac {2}{7}}, K({\tfrac {1}{2}}, {\tfrac {1}}{\sqrt {2}}, =\tbigl \{}{\tfrac {1}{2}}, \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}, {\sqrt {2\sin ({\tfrac {1}{7}\pi )},\cot ({\tfrac {3}{28}\pi )},+\sin ({\tfrac {1}{14}\pi ){\bigr \}}}, {\bigr \}} cn [ 4 7 K ( 1 2 2 ) ; 1 2 2 ] = 탄 { 1 2 아치형의 [ 1 2 2 cos ( 1 14 π ) 태닝한 ( 5 28 π ) + 죄악의 ( 3 14 π ) ] } {\displaystyle \operatorname {cn} [{\tfrac {4}{7}}, K({\tfrac {1}{2}}, {\tfrac {2}}, {\sqrt {2}}, =\tbigl \{}{\tfrac {1}{2}}, \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}, {\sqrt {2\cos ({\tfrac {1}{14}\pi )}, +\sin ({\tfrac {3}{14}\pi )}, {\bigr \}}, {\bigr \}} cn [ 6 7 K ( 1 2 2 ) ; 1 2 2 ] = 탄 { 1 2 아치형의 [ 1 2 2 cos ( 3 14 π ) 간이 침대 ( 1 28 π ) + cos ( 1 7 π ) ] } {\displaystyle \operatorname {cn} [{\tfrac {6}{7}}, K({\tfrac {1}{2}}, {\tfrac {1}}{\sqrt {2}}, =\tbigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos ({\tfrac {3}{14}\pi )}+\cos ({\tfrac {1}{28}\pi )}+\cos ({\tfrac {1}{7}\pi ){\bigr \}}} 대응하는 피타고라스의 반대에 대해서는 다음 공식이 유효합니다.
sn [ 2 7 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 { 1 2 아치형의 [ 1 2 2 죄악의 ( 1 7 π ) 간이 침대 ( 3 28 π ) + 죄악의 ( 1 14 π ) ] } {\displaystyle \operatorname {sn} [{\tfrac {2}{7}}, K({\tfrac {1}{2}}, {\tfrac {1}{2}}, {\sqrt {2}}, =\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}, \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}, {\sqrt {2\sin ({\tfrac {1}{7},\pi )\cot ({\tfrac {3}{28}},\pi )},+\sin ({\tfrac {1}{14},\pi ){\bigr \}}, {\bigr \} sn [ 4 7 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 { 1 2 아치형의 [ 1 2 2 cos ( 1 14 π ) 태닝한 ( 5 28 π ) + 죄악의 ( 3 14 π ) ] } {\displaystyle \operatorname {sn} [{\tfrac {4}{7}}, K({\tfrac {1}{2}}, {\tfrac {2}}, {\tfrac {sqrt {2}}, =\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}, \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}, {\sqrt {2\cos ({\tfrac {1}{14},\pi )}, +\sin ({\tfrac {3}{14},\pi )}, {\bigr ]}, {\bigr \}} sn [ 6 7 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 { 1 2 아치형의 [ 1 2 2 cos ( 3 14 π ) 간이 침대 ( 1 28 π ) + cos ( 1 7 π ) ] } {\displaystyle \operatorname {sn} [{\tfrac {6}{7}}, K({\tfrac {1}{2}}, {\tfrac {1}{2}}, {\sqrt {2}}, =\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}, \operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}, {\sqrt {2\cos({\tfrac {3}{14}\pi )\cot ({\tfrac {1}{28}},\pi )}}+\cos ({\tfrac {1}{7}\pi ){\bigr \}}{\bigr \} 중요 ID:
k 2 {\displaystyle tfrac 1}{2}}{\sqrt 2}}} 다음 타원 함수 sl {\displaystyle \operatorname } {\displaystyle \operatorname cl} 가)
슬 ( u ) = 1 2 2 sd ( 2 u ; 1 2 2 ) = 1 2 2 sn ( 2 u ; 1 2 2 ) dn ( 2 u ; 1 2 2 ) , cl ( u ) = cn ( 2 u ; 1 2 2 ) . {\displaystyle \operatorname {sl}(u)={\tfrac {1}{2}}\,\operatorname {sd}({\sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}\,,)={\tfrac {1}{2}}{\sqrt {2}\,u;{\tfrac {1}{2}\,u;{\tfrac {2}}{\sqrt {2}}\,u;{\tfrac {dn}({\sqrt {2}}){,u;{\tfrac {1}{2}}{\sqrt {2}\,}},\quad \operatorname {cl}(u)=\operatorname {cn}({) \sqrt {2}}\,u;{\tfrac {1}{2}}{\sqrt {2}\,,). } k {\displaystyle i} sl {\displaystyle \operatorname {sl}} cl {\displaystyle \operatorname {cl}이(
슬 ( u ) = sn ( u ; i ) , cl ( u ) = 씨디 ( u ; i ) = cn ( u ; i ) dn ( u ; i ) . {\displaystyle \operatorname {sl}(u)=\operatorname {sn}(u;i),\quad \operatorname {cl}(u)=\operatorname {cd}(u;i)={\frac {\operatorname {cn}(u;i)}{\operatorname {dn}(u;i)}}} 등하모닉 값 모듈러스 k sin 112 ( 3 ) {\displaystyle sin tfrac {1}{12}\pi 3) k cos 112 ( 13 {\displaystyle cos tfrac {1}{12}\pi tfrac {1}{3}}}) 등하모닉 케이스 의 값이라고 합니다.
cn { 2 5 K [ 죄악의 ( 1 12 π ) ] ; 죄악의 ( 1 12 π ) } = 태닝한 { 아크탄 [ 10 3 태닝한 ( 1 10 π ) + 1 3 3 ( 10 3 − 1 ) ] − 1 12 π } {\displaystyle \operatorname {cn} \{\tfrac {2}{5}}K{\bigl [}\sin ({\tfrac {1}{12}\pi ){\bigr ]};\sin ({\tfrac {1}{12}\pi )\}=\tan {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}\tan ({\tfrac {1}{10}\pi )+{\tfrac {1}{3}}{\sqrt {3}}}{({\sqrt[3}}-1){\bigr ]}-{\tfrac {1}{12}}\pi {\bigr \}} cn { 4 5 K [ 죄악의 ( 1 12 π ) ] ; 죄악의 ( 1 12 π ) } = 태닝한 { 아크탄 [ 10 3 태닝한 ( 1 10 π ) − 1 3 3 ( 10 3 − 1 ) ] + 1 12 π } {\displaystyle \operatorname {cn} \{\tfrac {4}{5}}K{\bigl [}\sin ({\tfrac {1}{12}\pi ){\bigr ]};\sin ({\tfrac {1}{12}\pi )\}=\tan {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}\tan ({\tfrac {1}{10}\pi )-{\tfrac {1}{3}}{\sqrt {3}}}{({\sqrt[3}}-1}{\bigr ]}+{\tfrac {1}{12}}\pi {\bigr \}} cn { 2 5 K [ cos ( 1 12 π ) ] ; cos ( 1 12 π ) } = 간이 침대 { 아크탄 [ 10 3 간이 침대 ( 1 5 π ) + 1 3 3 ( 10 3 − 1 ) ] − 1 12 π } {\displaystyle \operatorname {cn} \{\tfrac {2}{5}}K{\bigl [}\cos ({\tfrac {1}{12}\pi){\bigr ]};\cos ({\tfrac {1}{12}\pi)\}=\cot {\bigl \{}\arctan {\bigl [}{\cot ({\tfrac {1}{5}\pi)+{\tfrac {1}{3}}{\sqrt {3}}{({\sqrt[3}}-1){\bigr ]}-{\tfrac {1}{12}}\pi {\bigr \}} cn { 4 5 K [ cos ( 1 12 π ) ] ; cos ( 1 12 π ) } = 간이 침대 { 아크탄 [ 10 3 간이 침대 ( 1 5 π ) − 1 3 3 ( 10 3 − 1 ) ] + 1 12 π } {\displaystyle \operatorname {cn} \{\tfrac {4}{5}}K{\bigl [}\cos ({\tfrac {1}{12}\pi ){\bigr ]};\cos ({\tfrac {1}{12}\pi )\}=\cot {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}\cot ({\tfrac {1}{5}\pi )-{\tfrac {1}{3}}({\sqrt[3}}-1){\bigr ]}+{\tfrac {1}{12}}\pi {\bigr \}} 꽃은 타원형 람다 별 기능 을 표시합니다!
기초함수 k 0 {\displaystyle 0} k 1 {\displaystyle 1} .
기능. k = 0k = 1 sn ( u ; k ) {\displaystyle \operatorname {sn}(u;k)} 죄악의 u {\displaystyle \sinu} 탄 u {\displaystyle \tanhu} cn ( u ; k ) {\displaystyle \operatorname {cn}(u;k)} cos u {\displaystyle \cosu} 뒤지다 u {\displaystyle \operatorname {sech} u} dn ( u ; k ) {\displaystyle \operatorname {dn}(u;k)} 1 {\displaystyle 1} 뒤지다 u {\displaystyle \operatorname {sech} u} ns ( u ; k ) {\displaystyle \operatorname {ns}(u;k)} csc u {\displaystyle \cscu} 요람을 깔다 u {\displaystyle \cothu} nc ( u ; k ) {\displaystyle \operatorname {nc}(u;k)} 초 u {\displaystyle \secu} 으스스한 u {\displaystyle \coshu} nd ( u ; k ) {\displaystyle \operatorname {nd}(u;k)} 1 {\displaystyle 1} 으스스한 u {\displaystyle \coshu} sd ( u ; k ) {\displaystyle \operatorname {sd}(u;k)} 죄악의 u {\displaystyle \sinu} 죄스러운 u {\displaystyle \sinhu} 씨디 ( u ; k ) {\displaystyle \operatorname {cd}(u;k)} cos u {\displaystyle \cosu} 1 {\displaystyle 1} cs ( u ; k ) {\displaystyle \operatorname {cs}(u;k)} 간이 침대 u {\displaystyle \cotu} csch u {\displaystyle \operatorname {csch} u} ds ( u ; k ) {\displaystyle \operatorname {ds}(u;k)} csc u {\displaystyle \cscu} csch u {\displaystyle \operatorname {csch} u} dc ( u ; k ) {\displaystyle \operatorname {dc}(u;k)} 초 u {\displaystyle \secu} 1 {\displaystyle 1} sc ( u ; k ) {\displaystyle \operatorname {sc}(u;k)} 태닝한 u {\displaystyle \tanu} 죄스러운 u {\displaystyle \sinhu}
자코비 진폭의 경우 ( u ; 0 ) {\displaystyle \operatorname {am}(u;0 u} ( u ; 1 ) gd u {\displaystyle \operatorname {am}(u;1 operatorname {gd}u} gd {\displaystyle \operatorname {gd} ( Gudermannian 함수 입니다.
일반적으로 둘 다 p가 아니면 q는 d이고 pq u ; u displaystyle operatorname u;1) operatorname operatorname u);0) .
아이덴티티 덧셈 정리 함수는 범례 형식에서모듈러스 {\displaystyle k}
cn 2 ( u ; k ) + sn 2 ( u ; k ) = 1 , {\displaystyle \operatorname {cn} ^{2}(u;k)+\operatorname {sn} ^{2}(u;k)=1,\,}
dn 2 ( u ; k ) + k 2 sn 2 ( u ; k ) = 1. {\displaystyle \operatorname {dn} ^{2}(u;k)+k^{2}\operatorname {sn} ^{2}(u;k)=1.\,}
이로부터 우리는 (cn, sn, dn)이 위의 두 방정식에 의해 정의된 두 쿼드릭 의 교차점인 타원 곡선 을 매개 변수화한다는 것을 알 수 있습니다. 이제 자코비 함수에[3] [21]
sn ( x + y ; k ) = sn ( x ; k ) cn ( y ; k ) dn ( y ; k ) + sn ( y ; k ) cn ( x ; k ) dn ( x ; k ) 1 − k 2 sn 2 ( x ; k ) sn 2 ( y ; k ) , cn ( x + y ; k ) = cn ( x ; k ) cn ( y ; k ) − sn ( x ; k ) sn ( y ; k ) dn ( x ; k ) dn ( y ; k ) 1 − k 2 sn 2 ( x ; k ) sn 2 ( y ; k ) , dn ( x + y ; k ) = dn ( x ; k ) dn ( y ; k ) − k 2 sn ( x ; k ) sn ( y ; k ) cn ( x ; k ) cn ( y ; k ) 1 − k 2 sn 2 ( x ; k ) sn 2 ( y ; k ) . {\displaystyle {\begin{aligned}\operator name {sn}(x+y;k) &={\operatorname {sn}(x;k)\operatorname {cn}(y;k)\operatorname {dn}(y;k)+\operatorname {cn}(x;k)\operatorname {dn}(x;k) \over {1-k^{2}(x;k)\operatorname {sn}^{2}(x;k)\operatorname {sn}^{2}(y;k)},\[8pt]\operatorname {cn}(x+y;k) &={\operatorname {cn}(x;k)\operatorname {cn}(y;k)-\operatorname {sn}(x;k)\operatorname {dn}(x;k)\operatorname {dn}(x;k) \over {1-k^{2}(x;k)\operatorname {sn}^{2}(x;k)\operatorname {sn}^{2}(y;k)},\[8pt]\operatorname {dn}(x+y;k) &={\operatorname {dn}(x;k)\operatorname {dn}(y;k)-k^{2}\operatorname {sn}(x;k)\operatorname {cn}(x;k)\operatorname {cn}(y;k) \over {1-k^{2}\operatorname {sn}^{2}(x;k)\operatorname {sn}^{2}(y;k)}. \end{aligned}}
함수 sn과 cd만 처리하면 두 정리가 서로 반대칭인 다음과 같은 덧셈 정리 쌍을 설정할 수 있습니다.
sn ( x + y ; k ) = sn ( x ; k ) 씨디 ( y ; k ) + 씨디 ( x ; k ) sn ( y ; k ) 1 + k 2 sn ( x ; k ) 씨디 ( x ; k ) sn ( y ; k ) 씨디 ( y ; k ) {\displaystyle {\color {blueviolet}\operator name {sn}(x+y;k) = {\frac {{\color {blueviolet}\operatorname {sn}(x;k)\, {\color {blue}\operatorname {cd}(y;k)\color {blue}\operatorname {cd}(x;k)\, {\color {blueviolet}\operatorname {sn}(y;k){1+k^{2}\, {\color {blueviolet}\operatorname {sn}(x;k)\, {\color {blueviolet}\operatorname {sn}(y;k){\color {blue}\operatorname {cd}(y;k)}} 씨디 ( x + y ; k ) = 씨디 ( x ; k ) 씨디 ( y ; k ) − sn ( x ; k ) sn ( y ; k ) 1 − k 2 sn ( x ; k ) 씨디 ( x ; k ) sn ( y ; k ) 씨디 ( y ; k ) {\displaystyle {\color {blue}\operator name {cd}(x+y;k) = {\frac {{color {blue}\operatorname {cd}(x;k)\, {\color {blue}\operatorname {cd}(y;k)-{\color {blueviolet}\operatorname {sn}(x;k)\, {\color {blueviolet}\operatorname {sn}(y;k){1-k^{2}\, {\color {blueviolet}\operatorname {sn}(x;k)\, {\color {blueviolet}\operatorname {cd}(x;k)\, {\color {blueviolet}\operatorname {sn}(y;k)\, {\color {blue}\operator name {cd}(y;k)}}
자코비엡실론과 zn 함수는 준가산 정리를 만족합니다.
E ( x + y ; k ) = E ( x ; k ) + E ( y ; k ) − k 2 sn ( x ; k ) sn ( y ; k ) sn ( x + y ; k ) , zn ( x + y ; k ) = zn ( x ; k ) + zn ( y ; k ) − k 2 sn ( x ; k ) sn ( y ; k ) sn ( x + y ; k ) . {\displaystyle {\begin{aligned}{\mathcal {E}}(x+y;k) &={\mathcal {E}}(x;k)+{\mathcal {E}}(y;k)-k^{2}\연산자 이름 {sn}(x;k)\연산자 이름 {sn}(y;k)\연산자 이름 {sn}(x+y;k), \\\\operator name {zn} (x+y;k) &=\operatorname {zn}(x;k)+\operatorname {zn}(y;k)-k^{2}\operatorname {sn}(x;k)\operatorname {sn}(y;k)(x+y;k)입니다. \end{aligned}}
이중각 공식은 x = y 를 설정함으로써 위의 식들로부터 쉽게 유도될 수 있습니다. 반각 공식은[18] [3]
p q. ( 1 2 u ; k ) 2 = f p / f q {\displaystyle \operatorname {pq}({\tfrac {1}{2}u;k)^{2}=f_{\mathrm {p}}/f_{\mathrm {q}}}
여기서:
f c = cn ( u ; k ) + dn ( u ; k ) {\displaystyle f_{\mathrm {c} =\operator name {cn}(u;k)+\operator name {dn}(u;k)} f s = 1 − cn ( u ; k ) {\displaystyle f_{\mathrm {s} = 1-\operator name {cn}(u;k)} f n = 1 + dn ( u ; k ) {\displaystyle f_{\mathrm {n} = 1+\operator name {dn}(u;k)} f d = ( 1 + dn ( u ; k ) ) − m ( 1 − cn ( u ; k ) ) {\displaystyle f_{\mathrm {d} =(1+\operatorname {dn}(u;k))-m(1-\operatorname {cn}(u;k))}
반각 공식 다음 세 가지 공식은 반의 정리를 설명합니다.
sn ( u 2 ; k ) 2 = 1 − cn ( u ; k ) 1 + dn ( u ; k ) {\displaystyle \operatorname {sn} \left ({\frac {u}{2};k\right)^{2}={\frac {1-\operatorname {cn}(u;k)}{1+\operatorname {dn}(u;k)}} cn ( u 2 ; k ) 2 = cn ( u ; k ) + dn ( u ; k ) 1 + dn ( u ; k ) {\displaystyle \operatorname {cn} \left ({\frac {u}{2};k\right)^{2}={\frac {\operatorname {cn}(u;k)+\operatorname {dn}(u;k){1+\operatorname {dn}(u;k)}} dn ( u 2 ; k ) 2 = 1 − k 2 + dn ( u ; k ) + k 2 cn ( u ; k ) 1 + dn ( u ; k ) {\displaystyle \operatorname {dn} \left ({\frac {u}{2};k\right)^{2}={\frac {1-k^{2}+\operatorname {dn}(u;k)+k^{2}\operatorname {cn}(u;k)}{1+\operatorname {dn}(u;k)}
그리고 산술평균 의 정리는 다음 공식으로 설명됩니다.
sn ( 1 2 x + 1 2 y ; k ) 2 = 1 + sn ( x ; k ) sn ( y ; k ) − cn ( x ; k ) cn ( y ; k ) 1 + k 2 sn ( x ; k ) sn ( y ; k ) + dn ( x ; k ) dn ( y ; k ) {\displaystyle \operatorname {sn} {\bigl(}{\frac {1}{2}}\,x+{\frac {1}{2}}\,y;\,k{\bigr}^{2}={\frac {1+\operatorname {sn}(x;k)\operatorname {sn}(y;k)-\operatorname {cn}(x;k)\operatorname {cn}(y;k){1+k^{2}\operatorname {sn}(x;k)+\operatorname {dn}(x;k)}\operatorname {dn}(y;k)} K공식 반K공식
sn [ 1 2 K ( k ) ; k ] = 2 1 + k + 1 − k {\displaystyle \operatorname {sn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {\sqrt {2}}{{\sqrt {1+k}}{{\sqrt {1-k}}}}
cn [ 1 2 K ( k ) ; k ] = 2 1 − k 2 4 1 + k + 1 − k {\displaystyle \operatorname {cn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {{\sqrt {2}}\,{\sqrt[{4}]{1-k^{2}}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}
dn [ 1 2 K ( k ) ; k ] = 1 − k 2 4 {\displaystyle \operatorname {dn} \left[{\tfrac {1}{2}}K(k);k\right]={\sqrt[{4}]{1-k^{2}}}
세 번째 K 공식
또한 이 방정식은[21] K 의 3분의 1의 sn-값으로 이어집니다.
k 2 s 4 − 2 k 2 s 3 + 2 s − 1 = 0 {\displaystyle k^{2}s^{4}-2k^{2}s^{3}+2s-1=0} s = sn [ 1 3 K ( k ) ; k ] {\displaystyle s=\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]} 이들 방정식은 자코비 함수의 다른 값으로 이어집니다.
cn [ 2 3 K ( k ) ; k ] = 1 − sn [ 1 3 K ( k ) ; k ] {\displaystyle \operatorname {cn} \left[{\tfrac {2}{3}}K(k);k\right]=1-\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]} dn [ 2 3 K ( k ) ; k ] = 1 / sn [ 1 3 K ( k ) ; k ] − 1 {\displaystyle \operatorname {dn} \left[{\tfrac {2}{3}}K(k);k\right]=1/\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]-1} 지금 언급된 4차 방정식에 기초하여 우리는 4차 방정식의 일반적인 경우 에 대한 해 알고리즘을 사용하여 단순화된 공식을 만들 수 있습니다. 이 매개 변수화된 공식은 다음과 같은 방식으로 생성할 수 있습니다.
sn ⟨ 1 3 K { 태닝한 [ 1 2 아크탄 ( x 3 ) ] } ; 태닝한 [ 1 2 아크탄 ( x 3 ) ] ⟩ = 탄 [ 1 2 ln ( 2 x 4 − x 2 + 1 − x 2 + 2 + x 2 + 1 ) ] {\displaystyle \operatorname {sn} {\biggl \ langle} {\frac {1}{3}}K{\bigl \{}\tan {\bigl [}{\frac {1}{2}}\ctan {\bigl (}x^{3}{\bigr ]}{\bigr \};\tan {\bigl [}{\frac {1}{2}},\tan {\bigl (}x^{3}{\bigr}}{\bigr ]{\bigr}{\bigr}}{\biggr \rangle }=\tanh {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2}-x^{2}+2}}}+{\sqrt {x^{2}+1}}{\bigr. )}{\bigr ]}} 피타고라스의 반대는 다음과 같은 공식을 연속적으로 제시합니다.
cn ⟨ 1 3 K { 태닝한 [ 1 2 아크탄 ( x 3 ) ] } ; 태닝한 [ 1 2 아크탄 ( x 3 ) ] ⟩ = 뒤지다 [ 1 2 ln ( 2 x 4 − x 2 + 1 − x 2 + 2 + x 2 + 1 ) ] {\displaystyle \operatorname {cn} {\biggl \ langle} {\frac {1}{3}}K{\bigl \{}\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr ]}{\bigr \};\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr ]}{\bigr ]}{\biggr \rangle } =\operatorname {sech} {\bigl [}{\frac {1}}\ln {\bigl (}{\sqrt {2}-x^{2}+2}}+{\sqrt {2}}+{\sqrt {xx}}+{sqrt {x} ^{2}+1}}{\bigr )}{\bigr ]}} 이제 언급된 이 두 공식은 x 의 모든 실수 값에 대해 유효하며, 기준 R displaystyle x\in \mathbb {R}}
x 를 얻기 위해, 우리는 모듈러스의 아크탄젠트의 두 배의 접선을 취한 다음 x 가 나타나도록 입방체근 을 취합니다.
그런 다음 생성된 값 x 를 매개변수화된 방정식의 균형의 오른쪽에 삽입합니다.
이 계산 알고리즘과 관련하여 다음 세 가지 예를 제시합니다.
첫번째 예: 1 2 2 = 태닝한 [ 1 2 아크탄 ( x 3 ) ] ( x = 2 ) {\displaystyle {\frac {1}{2}}{\sqrt {2}}=\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt {2}\,) 위에 표시된 분수에 x 2 {\ displaystyle sqrt {2}\,}
sn [ 1 3 K ( 1 2 2 ) ; 1 2 2 ] = 탄 [ 1 2 ln ( 12 4 + 3 ) ] = 1 2 ( 12 4 − 3 + 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}},{\bigr )};{\frac {1}{2}},{\sqrt {2},{\bigr ]}=\tanh {\bigl [}{\frac {1}{2}},{\n{\bigl (}{\sqrt [{4}]{12}}+{\sqrt {3}{\bigr ]}={\frac {1}{2}}({\sqrt[4}}{12}-{\sqrt {3}+1)} cn [ 1 3 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 [ 1 2 ln ( 12 4 + 3 ) ] = 2 3 − 3 4 {\displaystyle \operatorname {cn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}},{\bigr )};{\frac {1}{2}},{\sqrt {2},{\bigr ]}=\operatorname {sech} {\bigl [}{\frac {1}{2}},{\ln {\bigl (}{\sqrt[{4}}},{\bigr )}{\bigr ]}={\sqrt[{4}}{2}-3}}}
제5 K공식
다음 방정식은 다음과 같은 해를 갖습니다.
4 k 2 t 6 + 8 k 2 t 5 + 2 ( 1 − k 2 ) 2 t − ( 1 − k 2 ) 2 = 0 {\displaystyle 4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0} t = 1 2 − 1 2 k 2 sn [ 2 5 K ( k ) ; k ] 2 sn [ 4 5 K ( k ) ; k ] 2 = sn [ 4 5 K ( k ) ; k ] 2 − sn [ 2 5 K ( k ) ; k ] 2 2 sn [ 2 5 K ( k ) ; k ] sn [ 4 5 K ( k ) ; k ] {\displaystyle t={\frac {1}{2}}-{\frac {1}{2}^{2}\operatorname {sn} \left[{\tfrac {2}{5}}K(k);k\right]^{2}\operatorname {sn} \left[{\tfrac {4}{5}}K(k);k\right]^{2}={\frac {4}{5}K(k);k\right]^{2}-\operatorname {sn} \left[{\frac {5}}K(k);k\right]^{2}\left[{\frac {2}{5}}K(k);k\right]^{2}{2}{2\operatorname {sn} \left[{\frac {2}{5}}K(k);k\right]\operatorname {sn} rname {sn} \left[{\frac {4}{5}}K(k);k\right]} }} sn-값을 구하기 위해 해 x를 다음 식으로 표현합니다.
sn [ 2 5 K ( k ) ; k ] = ( 1 + k 2 ) − 1 / 2 2 ( 1 − t − t 2 ) ( t 2 + 1 − t t 2 + 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}};k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1}) }}} sn [ 4 5 K ( k ) ; k ] = ( 1 + k 2 ) − 1 / 2 2 ( 1 − t − t 2 ) ( t 2 + 1 + t t 2 + 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1}) }}} 0과 반 사이의 t 해가 이들 식에 사용되어야 하는 해입니다.
지금 언급된 계산 알고리즘과 관련하여 중요한 예는 다음과 같습니다.
6도 방정식은 다음과 같이 주어집니다. 4 k 2 t 6 + 8 k 2 t 5 + 2 ( 1 − k 2 ) 2 t − ( 1 − k 2 ) 2 = 0 {\displaystyle 4k^{2}t^{6}+8k^{2}t^{5}+2(1-k^{2})^{2}t-(1-k^{2})^{2}=0} 이 1 displaystyle tfrac 2}}{\sqrt }}}
이 모듈러스 값을 입력하고 전체 방정식에 인수 4를 곱하면 다음과 같은 방정식을 얻을 수 있습니다.
8 t 6 + 16 t 5 + 2 t − 1 = 0 {\displaystyle 8t^{6}+16t^{5}+2t-1=0} 0과 반 사이에 위치한 식 fort의 해는 다음과 같습니다.
t = 1 4 ( 5 + 1 ) ( 5 4 − 1 ) {\displaystyle t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}-1)} 이 해 t와 해당 모듈러스 k는 진폭 사인 값에 대한 공식에 삽입됩니다.
sn [ 2 5 K ( 1 2 2 ) ; 1 2 2 ] = ( 1 + k 2 ) − 1 / 2 2 ( 1 − t − t 2 ) ( t 2 + 1 − t t 2 + 1 ) [ k = 1 2 2 ∩ t = 1 4 ( 5 + 1 ) ( 5 4 − 1 ) ] {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}\, {\tfrac {2}},{\sqrt {2}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1-t{t^{2}+1}) },{\bigl [}k={\tfrac {1}{2}},{\sqrt {2}},\cap \,t={\tfrac {1}{4}}({\sqrt {5}+1)({\sqrt[4}]{5}-1){\bigr ]}} sn [ 4 5 K ( 1 2 2 ) ; 1 2 2 ] = ( 1 + k 2 ) − 1 / 2 2 ( 1 − t − t 2 ) ( t 2 + 1 + t t 2 + 1 ) [ k = 1 2 2 ∩ t = 1 4 ( 5 + 1 ) ( 5 4 − 1 ) ] {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}\, {\tfrac {2}},{\sqrt {2}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1+t{\sqrt {t^{2}+1}) },{\bigl [}k={\tfrac {1}{2}},{\sqrt {2}},\cap \,t={\tfrac {1}{4}}({\sqrt {5}+1)({\sqrt[4}]{5}-1){\bigr ]}} 이렇게 하면 특수 값의 섹션에 이미 언급된 다음과 같은 결과가 나타납니다.
sn [ 2 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 2 태닝한 ( 1 20 π ) 4 ( 간이 침대 ( 1 10 π ) + 1 − 간이 침대 ( 1 10 π ) − 3 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[4}]{2\tan ({\tfrac {1}{20}\pi )},({\sqrt {\cot ({\tfrac {1}{10}\pi )},{\sqrt {\cot ({\tfrac {1}{10}\pi )+1}}-{\sqrt {\cot ({\tfrac {1}\pi )-3}}} sn [ 4 5 K ( 1 2 2 ) ; 1 2 2 ] = 1 2 2 간이 침대 ( 1 20 π ) 4 ( 간이 침대 ( 1 10 π ) + 3 − 간이 침대 ( 1 10 π ) − 1 ) {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[4}]{2\cot ({\tfrac {1}{20}\pi )},({\sqrt {\cot ({\tfrac {1}{10}\pi )+3},{\sqrt {\cot ({\tfrac {1}{10}\pi )-{\cot rt\tfrac {1}\pi )-1}} 쌍곡선 함수 를 사용하면 다음과 같은 동등한 식을 만들 수 있습니다.
sn [ 2 5 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 { 1 2 아치형의 [ 1 2 간이 침대 ( 1 10 π ) − 1 2 ] } {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}},{\sqrt {2}},{\bigr ]}=\operatorname {sech}{\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth}{\bigl [}{\tfrac {1}{2}}\cot {\bigl (}{\tfrac {1}{10}\pi {\bigr )}-{\tfrac {1}{2}}-{\bigr ]}{\bigr \}} sn [ 4 5 K ( 1 2 2 ) ; 1 2 2 ] = 뒤지다 { 1 2 아치형의 [ 1 2 간이 침대 ( 1 10 π ) + 1 2 ] } {\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}, {\bigr ]}=\operatorname {sech}{\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth}{\bigl [}{\tfrac {1}{2}}\cot {\bigl (}{\tfrac {1}{10}}\pi {\bigr}+{\tfrac {1}{2}}{\bigr}}{\bigr \}}
아벨 러피니 정리 에 따르면, 타원 모듈러스의 정칙적인 경우에 대해 완전한 제1종 타원 적분의 5분의 1의 진폭 사인 값에 대한 기본 식을 설정하는 것은 완전히 불가능합니다.
함수의 제곱 간의 관계 함수의 제곱 간의 관계는 두 가지 기본 관계에서 도출할 수 있습니다(Arguments (u ,m ) 억제됨).
cn 2 + sn 2 = 1 {\displaystyle \operatorname {cn}^{2}+\operatorname {sn}^{2}=1} cn 2 + m ′ sn 2 = dn 2 {\displaystyle \operatorname {cn} ^{2}+m'\operatorname {sn} ^{2}=\operatorname {dn} ^{2}} 여기서 m + m' = 1. 형태 nq 의 임의의 함수를 곱하면 더 일반적인 방정식이 됩니다.
cq 2 + 사각형의 2 = nq 2 {\displaystyle \operatorname {cq} ^{2}+\operatorname {sq} ^{2}=\operatorname {nq} ^{2}} cq 2 + m ′ 사각형의 2 = dq 2 {\displaystyle \operatorname {cq} ^{2}{}+m'\operatorname {sq} ^{2}=\operatorname {dq} ^{2}}
q = d일 때, 이것들은 단위 원에 대한 방정식(x y 2 r displaystyle 2} ^{ }= r ^{2 타원 (x2 m' y 2 = {\displaystyle ^{2}{} m'y^{2} = 1 }), = y = 및 r = 곱셈 규칙을 사용하면 다른 관계를 유도할 수 있습니다. 예를 들어,
− dn 2 + m ′ = − m cn 2 = m sn 2 − m {\displaystyle -\operatorname {dn} ^{2}{}+m'=-m\operatorname {cn} ^{2}=m\operatorname {sn} ^{2}-m}
− m ′ nd 2 + m ′ = − m m ′ sd 2 = m 씨디 2 − m {\displaystyle -m'\operatorname {nd} ^{2}{}+m'=-mm'\operatorname {sd} ^{2}=m\operatorname {cd} ^{2}-m}
m ′ sc 2 + m ′ = m ′ nc 2 = dc 2 − m {\displaystyle m'\operatorname {sc} ^{2}{}+m'=m'\operatorname {nc} ^{2}=\operatorname {dc} ^{2}-m}
cs 2 + m ′ = ds 2 = ns 2 − m {\displaystyle \operatorname {cs} ^{2}{}+m'=\operatorname {ds} ^{2}=\operatorname {ns} ^{2}-m}
Theta 함수를 통한 함수 값 표현 수학자 에드먼드 테일러 휘태커 (Edmund Taylor Whittaker )와 조지 네빌 왓슨(George Neville Watson [22] [23] [24] 세타 널버트 함수 의 곱 정의는 다음과 같습니다.
ϑ 00 ( w ) = ∏ n = 1 ∞ ( 1 − w 2 n ) ( 1 + w 2 n − 1 ) 2 {\displaystyle \vartheta _{00}(w)=\prod _{n=1}^{\infty}(1-w^{2n})(1+w^{2n-1})^{2}} ϑ 01 ( w ) = ∏ n = 1 ∞ ( 1 − w 2 n ) ( 1 − w 2 n − 1 ) 2 {\displaystyle \vartheta _{01}(w)=\prod _{n=1}^{\infty}(1-w^{2n})(1-w^{2n-1})^{2}} 적분 K {\displaystyle K} :
모듈의 타원 명사의 소위 세타 영값 함수를 사용하면 많은 야코비안 함수 값을 나타낼 수 있습니다.
sc [ 2 3 K ( k ) ; k ] = 3 ϑ 01 [ q ( k ) 6 ] 1 − k 2 ϑ 01 [ q ( k ) 2 ] {\displaystyle \operatorname {sc} [{\tfrac {2}{3}}K(k);k]={\frac {{\sqrt {3}}\,\vartheta _{01}[q(k)^{6}}{\sqrt {1-k^{2}}\,\vartheta _{01}[q(k)^{2}}} sn [ 1 3 K ( k ) ; k ] = 2 ϑ 00 [ q ( k ) ] 2 3 ϑ 00 [ q ( k ) 3 ] 2 + ϑ 00 [ q ( k ) ] 2 = 3 ϑ 01 [ q ( k ) 3 ] 2 − ϑ 01 [ q ( k ) ] 2 3 ϑ 01 [ q ( k ) 3 ] 2 + ϑ 01 [ q ( k ) ] 2 {\displaystyle \operatorname {sn} [{\tfrac {1}{3}}K(k);k]={\frac {2\,\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)]^{2}+\vartheta _{00}[q(k)]^{2}}={\frac {3\,\vartheta _{01}[q(k)]^{3}^{2}-\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)]^{2}+\vartheta _{01}[2}}} cn [ 2 3 K ( k ) ; k ] = 3 ϑ 00 [ q ( k ) 3 ] 2 − ϑ 00 [ q ( k ) ] 2 3 ϑ 00 [ q ( k ) 3 ] 2 + ϑ 00 [ q ( k ) ] 2 = 2 ϑ 01 [ q ( k ) ] 2 3 ϑ 01 [ q ( k ) 3 ] 2 + ϑ 01 [ q ( k ) ] 2 {\displaystyle \operatorname {cn} [{\tfrac {2}{3}}K(k);k]={\frac {3\,\vartheta _{00}[q(k)^{3}]^{2}-\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)]^{2}+\vartheta _{00}[q(k)]^{2}}={\frac {2\,\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)]^{2}+\vartheta _{01}[2}}}} 적분 K {\displaystyle K} :
sn [ 1 5 K ( k ) ; k ] = { 5 ϑ 01 [ q ( k ) 5 ] ϑ 01 [ q ( k ) ] − 1 } { 5 ϑ 01 [ q ( k ) 10 ] 2 ϑ 01 [ q ( k ) 2 ] 2 − 1 } − 1 {\displaystyle \operatorname {sn} [{\tfrac {1}{5}}K(k);k]={\biggl \{}{\frac {\sqrt {5}}\,\vartheta _{01}[q(k)^{5}}{\biggr \}{\biggl \}{\biggl \}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}{\vartheta _{01}[q(k)^{2}}-1{\biggr \}^{-1}}^{-1}. sn [ 3 5 K ( k ) ; k ] = { 5 ϑ 01 [ q ( k ) 5 ] ϑ 01 [ q ( k ) ] + 1 } { 5 ϑ 01 [ q ( k ) 10 ] 2 ϑ 01 [ q ( k ) 2 ] 2 − 1 } − 1 {\displaystyle \operatorname {sn} [{\tfrac {3}{5}}K(k);k]={\biggl \{}{\frac {\sqrt {5}}\,\vartheta _{01}[q(k)^{5}}}{\biggr \}}{\biggl \}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}}-1{\biggr \}^{-1}}^{-1}^{-1}. cn [ 2 5 K ( k ) ; k ] = { 5 ϑ 00 [ q ( k ) 5 ] ϑ 00 [ q ( k ) ] + 1 } { 5 ϑ 01 [ q ( k ) 10 ] 2 ϑ 01 [ q ( k ) 2 ] 2 − 1 } − 1 {\displaystyle \operatorname {cn} [{\tfrac {2}{5}}K(k);k]={\biggl \{}{\frac {\sqrt {5}}\,\vartheta _{00}[q(k)^{5}}}{\vartheta _{00}[q(k)]}+1{\biggr \}{\biggl \}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}}}-1{\biggr \}^{-1} cn [ 4 5 K ( k ) ; k ] = { 5 ϑ 00 [ q ( k ) 5 ] ϑ 00 [ q ( k ) ] − 1 } { 5 ϑ 01 [ q ( k ) 10 ] 2 ϑ 01 [ q ( k ) 2 ] 2 − 1 } − 1 {\displaystyle \operatorname {cn} [{\tfrac {4}{5}}K(k);k]={\biggl \{}{\frac {\sqrt {5}}\,\vartheta _{00}[q(k)^{5}}{\biggr \}{\biggl \}{\biggl \}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}{\vartheta _{01}[q(k)^{2}}-1{\biggr \}^{-1}}^{-1} 세타 영값 함수와 타원형 의 기본 조합은 합리적으로 깨진 K-적분을 넘어 왼쪽 괄호 항목의 야코비안 함수 값을 표현하기에 충분하지 않습니다. 이를 위해서는 위에서 설명한 패턴의 0이 아닌 세타 함수가 필요합니다.
자코비 타원함수는 비선형 상미분방정식의 해로 작용합니다. 세 가지 기본 야코비 타원 함수의 도함수 는 다음과 같습니다.
d d z sn ( z ) = cn ( z ) dn ( z ) , {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}\operatorname {sn}(z)=\operatorname {cn}(z)\operatorname {dn}(z),} d d z cn ( z ) = − sn ( z ) dn ( z ) , {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}\operatorname {cn}(z)=-\operatorname {sn}(z)\operatorname {dn}(z),} d d z dn ( z ) = − m sn ( z ) cn ( z ) . {\displaystyle {\frac {\mathrm {d}}{\mathrm {d} z}\operatorname {dn}(z)=-m\operatorname {sn}(z)\operatorname {cn}(z)입니다.}
아래 표와 같이 다른 모든 함수의 도함수를 유도하는 데 사용할 수 있습니다(논거(u,m) 억제됨).
파생 변수 dupq ( u , m ) {\displaystyle {\frac {\mathrm {d} }\operator {pq}(u,m)} q c s n d p c 0 -dsns -dnsn -mandsd s dcnc 0 cndn cdnd n dcsc -csds 0 mcdsd d mncsc -csns -mcnsn 0
위의 덧셈 정리들 과 0 < m < 1의 주어진 m에 대하여 주요 함수들은 따라서 다음과 같은 비선형 통상 미분 방정식에 대한 해결책입니다.
sn {\displaystyle {\operatorname {sn} (x)} d 2 y d 2 ( m y - m y 3 = {\displaystyle {\frac {d} ^{2} mathrm d} ^{2 1 )y-2my ^ {3 0} dy d x ) 2 = ( 1 y 2 {\displaystyle \l ef t frac {d} y{\mathrm {d} x}\right) ^ {2 ^{2}}) cn x {\displaystyle \operatorname {cn} (x)} 미분방정식 d y 1 2 y 2 y 3 = displaystyle mathrm {d}^{2} mathrm {d} x^{ 1 2 y my ^ = = ( 1 y 2 {\displaystyle \l ef t frac {\mathrm {d } mathrm {d} x}}\right)^{2}=(1-y^{2})(1-m+my^{2})} dn {\displaystyle {dn} (x)} y 2 2 2 y 3 = {\displaystyle {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}} m) 2y ^ {3}= dy d x ) y 1 1 displaystyle \l ef t frac {d} y{\mathrm {d} x}\right) ^ {2 y^{2}-1)(1-m-y^{2}}} 자코비 진폭은 단순한 진자 의 정확한 운동을 설명하는 미분 방정식의 사소한 해결책을 제공합니다. 특히.
θ = 2 암 ( t 2 c 2 , 2 ) → d 2 θ d t 2 + c 죄악의 θ = 0. {\displaystyle \theta = 2\operatorname {am} \left ({\frac {t{\sqrt {2c}}{2}}, 2\right)\right 화살표 {\frac {\mathrm {d}^{2}\theta }{\mathrm {d} t^{2}}+c\sin \theta = 0.} 위 진자 미분방정식을 초기 각도 θ 0 {\displaystyle \theta _{0}}
θ = 2 호신 ( k 씨디 ( c t , k 2 ) ) , k = 죄악의 θ 0 2 . {\displaystyle \theta = 2\arcsin(k\operator name {cd}({\sqrt {c}}t,k^{2}),\quad k=\sin {\theta _{0}}{2}}}. Lambert 영상 시리즈 확장(명칭) 이름 을 q exp ( '( K( ei {\displaystyle exp pi K'(m)/K(m)) = e ^{i\pi \tau }}, Im ( τ ) 0 {\displaystyle \operatorname {Im} (\ tau 0 m = k {\displaystyle = k^{2}}, = π u 2K m )) {\displaystyle = pi (2K(m))} 합니다. 그러면 함수가 Lambert 영상 시리즈 로 확장됩니다.
sn ( u , m ) = 2 π k K ( m ) ∑ n = 0 ∞ q n + 1 / 2 1 − q 2 n + 1 죄악의 ( ( 2 n + 1 ) v ) , {\displaystyle \operatorname {sn}(u,m)={\frac {2\pi}{kK(m)}\sum _{n=0}^{\infty}{\frac {q^{n+1/2}}{1-q^{2n+1}}\sin((2n+1)v),} cn ( u , m ) = 2 π k K ( m ) ∑ n = 0 ∞ q n + 1 / 2 1 + q 2 n + 1 cos ( ( 2 n + 1 ) v ) , {\displaystyle \operatorname {cn}(u,m)={\frac {2\pi}{kK(m)}\sum _{n=0}^{\infty}{\frac {q^{n+1/2}}{1+q^{2n+1}}\cos((2n+1)v),} dn ( u , m ) = π 2 K ( m ) + 2 π K ( m ) ∑ n = 1 ∞ q n 1 + q 2 n cos ( 2 n v ) {\displaystyle \operatorname {dn}(u,m)={\frac {\pi}{2K(m)}}+{\frac {2\pi}{K(m)}}\sum _{n=1}^{\infty}{\frac {q^{n}}{1+q^{2n}}\cos(2nv)} zn ( u , m ) = 2 π K ( m ) ∑ n = 1 ∞ q n 1 − q 2 n 죄악의 ( 2 n v ) {\displaystyle \operatorname {zn}(u,m)={\frac {2\pi}{K(m)}\sum _{n=1}^{\infty}{\frac {q^{n}}{1-q^{2n}}\sin(2nv)} q exp ( Im )) {\displaystyle q\exp \left operatorname Im}(v)\right
자코비 진폭의 경우,
암 ( u , m ) = π u 2 K ( m ) + 2 ∑ n = 1 ∞ q n n ( 1 + q 2 n ) 죄악의 ( 2 n v ) {\displaystyle \operatorname {am}(u,m)={\frac {\piu}{2K(m)}}+2\sum _{n=1}^{\infty}{\frac {q^{n}}{n(1+q^{2n}}}\sin(2nv)} 여기서 0 m 1 {\displaystyle 0 1}, u R {\displaystyle u in \mathbb {R}}.
이변량 멱급수 확장이 Schett에 의해 발표되었습니다.[25]
빠른 계산 세타 함수비는 야코비 타원 함수를 계산하는 효율적인 방법을 제공합니다. 산술-기하학 평균 과 Landen의 변환 에 기초한 다른 방법이 있습니다.[6]
초기화
a 0 = 1 , b 0 = 1 − m , c 0 = 1 − b 0 2 {\displaystyle a_{0}=1,\,b_{0}={\sqrt {1-m}},c_{0}={\sqrt {1-b_{0}^{2}}}} 여기서 0 m 1 {\displaystyle 0 1
a n = a n − 1 + b n − 1 2 , b n = a n − 1 b n − 1 , c n = a n − 1 − b n − 1 2 {\displaystyle a_{n}={\frac {a_{n-1}+b_{n-1}}{2}},\,b_{n}={\sqrt {a_{n-1}b_{n-1}},\,c_{n}={\frac {a_{n-1}-b_{n-1}}{2}}} 여기 1 {\displaystyle n\geq 1
φ N = 2 N a N u {\displaystyle \varphi _{N}=2^{N}a_{N}u} u {\displaystyle \ in \mathbb {R}} 고정 N displaystyle N\in N} .
φ n − 1 = 1 2 ( φ n + 호신 ( c n a n 죄악의 φ n ) ) {\displaystyle \varphi _{n-1}={\frac {1}{2}}\left(\varphi _{n}+\arcsin \left ({\frac {c_{n}}{a_{n}}}\sin \varphi _{n}\right)\right)} n 1 {\displaystyle n\geq }
암 ( u , m ) = φ 0 {\displaystyle \operatorname {am}(u,m)=\varphi _{0} N {\displaystyle N\to \infty}. 그렇다면 실제 선의{\displaystyle \operatorname {am}}
타원 함수(일반적으로 복소수를 유지하는) 및 야코비 변환에 대한 덧셈 정리와 함께 위에서 설명한 계산 방법은 전체 복소수 평면에서 모든 야코비 타원 함수를 계산하는 데 사용될 수 있습니다.
자코비 진폭의 계산을 피하여 산술 기하학적 평균을 통해 자코비 타원 함수를 빠르게 계산하는 또 다른 방법은 허버트 E. 살저에 의한 것입니다.[26]
허락하다
0 ≤ m ≤ 1 , 0 ≤ u ≤ K ( m ) , a 0 = 1 , b 0 = 1 − m , {\displaystyle 0\leq m\leq 1,\,0\leq u\leq K(m),\,a_{0}=1,\,b_{0}={\sqrt {1-m}} a n + 1 = a n + b n 2 , b n + 1 = a n b n , c n + 1 = a n − b n 2 . {\displaystyle a_{n+1}={\frac {a_{n}+b_{n}}{2}},\,b_{n+1}={\sqrt {a_{n}b_{n}},\,c_{n+1}={\frac {a_{n}-b_{n}}{2}}}. 세트
y N = a N 죄악의 ( a N u ) y N − 1 = y N + a N c N y N y N − 2 = y N − 1 + a N − 1 c N − 1 y N − 1 ⋮ = ⋮ y 0 = y 1 + m 4 y 1 . {\displaystyle {\begin{aligned}y_{ N}&={\frac {a_{N}}{\sin(a_{N}u)}}\y_{N-1}&=y_{ N}+{\frac {a_{N}c_{ N}}{y_{ N}}\y_{N-2}&=y_{N-1}+{\frac {a_{N-1}c_{N-1}}{y_{N-1}}\\vdots &=\vdots \\y_{0}&=y_{1}+{\frac {m}{4y_{1}}. \end{aligned}} 그리고나서
sn ( u , m ) = 1 y 0 cn ( u , m ) = 1 − 1 y 0 2 dn ( u , m ) = 1 − m y 0 2 {\displaystyle {\begin{aligned}\operatorname {sn}(u,m)&={\frac {1}{y_{0}}\\\operatorname {cn}(u,m)&={\sqrt {1-{\frac {1}{y_{0}^{2}}}\\\operatorname {dn}(u,m)&={\sqrt {1-{\frac {m}{y_{0}^{2}}}\end{aligned}} N {\displaystyle N\to \infty} .
쌍곡선함수에 대한 근사치 야코비 타원 함수는 쌍곡 함수 측면에서 확장될 수 있습니다. m {\ displaystyle m} displaystyle m'^{2} '{\ displaystyle '} [27] [28]
sn(u ): sn ( u , m ) ≈ 탄 ( u ) + 1 4 m ′ ( 죄스러운 ( u ) 으스스한 ( u ) − u ) 뒤지다 2 ( u ) . {\displaystyle \operatorname {sn}(u,m)\approx \tanh(u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\operatorname {sech}^{2}(u)} cn(u ): cn ( u , m ) ≈ 뒤지다 ( u ) − 1 4 m ′ ( 죄스러운 ( u ) 으스스한 ( u ) − u ) 탄 ( u ) 뒤지다 ( u ) . {\displaystyle \operatorname {cn}(u,m)\approx \operatorname {sech}(u)-{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\tanh(u)\operatorname {sech}(u).} dn(u ): dn ( u , m ) ≈ 뒤지다 ( u ) + 1 4 m ′ ( 죄스러운 ( u ) 으스스한 ( u ) + u ) 탄 ( u ) 뒤지다 ( u ) . {\displaystyle \operatorname {dn}(u,m)\approx \operatorname {sech}(u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)+u)\tanh(u)\operatorname {sech}(u).} 자코비 진폭의 경우,
암 ( u , m ) ≈ gd ( u ) + 1 4 m ′ ( 죄스러운 ( u ) 으스스한 ( u ) − u ) 뒤지다 ( u ) . {\displaystyle \operatorname {am}(u,m)\approx \operatorname {gd}(u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\operatorname {sech}(u)}
연속분수 실수 a , 0인 p {\displaystyle a,p} nome q e i {\displaystyle e^{\pi i\ }, Im ) 타원 모듈러스 k( 1 k '( ) 2 10 00 2 {\textstyle k(\ {\ sqrt {1-k'(\ )^{2 vartheta _{10}(0;\ta u )/\vartheta _{00}(0;\ta )^{2}} 만약 [ τ = τ {\displaystyle [\tau = (\tau )} , K = π / 2 1 2, 1 2; 1 ; x displaystyle K(x ) pi / 2\cdot {}_{2}F_{1}(1/2, 1/2; 1;x^{2}}} 경우 , 다음 과 같은 연속적 인 분수 확장 을 갖는 것입니다.
dn ( ( p / 2 − a ) τ K [ p τ 2 ] ; k ( p τ 2 ) ) k ′ ( p τ 2 ) = ∑ n = − ∞ ∞ q p / 2 n 2 + ( p / 2 − a ) n ∑ n = − ∞ ∞ ( − 1 ) n q p / 2 n 2 + ( p / 2 − a ) n = − 1 + 2 1 − q a + q p − a 1 − q p + ( q a + q 2 p − a ) ( q a + p + q p − a ) 1 − q 3 p + q p ( q a + q 3 p − a ) ( q a + 2 p + q p − a ) 1 − q 5 p + q 2 p ( q a + q 4 p − a ) ( q a + 3 p + q p − a ) 1 − q 7 p + ⋯ {\displaystyle {\begin{aligned}&{\frac {p\textrm {dn}}\left((p/2-a))\tau K\left[{\frac {p\tau}{2}}\right];k\left({\frac {p\tau}{2}}\right)}{\sqrt {k'\left({\frac {p\tau}{2}}\right) }}={\frac {\sum _{n=-\infty}^{\infty}q^{p/2n^{2}+(p/2-a)n}}{\sum _{n=-\infty}^{\nfty}(-1)^{n}q^{p/2n^{2}+(p/2-a)n}}\[4pt]={&-1+{\frac {2}{1-{}}\,{\frac {q^{a}+q^{p-a}}{1-q^{p}+{}}\,{\frac {(q^{a}+q^{p-a}}(q^{a}+q^{p-a}){1-q^{3p}},{\frac {q^{p}(q^{a}+q^{3p-a}){1-q^{5p}},} {\frac {q^{2p}(q^{a}+q^{4p-a})(q^{a+3p}+q^{p-a}){1-q^{7p}+{}}\cdots \end{align}} 타원 모듈러스 k {\displaystyle k} sn ), cn {\textrm {sn}}(t), textrm {cn}(t)} dn t ) {\textrm {dn}(t)}
z C {\displaystyle z\in \mathbb {C}} k 1 {\displaystyle 1}
∫ 0 ∞ sn ( t ) e − t z d t = 1 1 2 ( 1 + k 2 ) + z 2 − 1 ⋅ 2 2 ⋅ 3 k 2 3 2 ( 1 + k 2 ) + z 2 − 3 ⋅ 4 2 ⋅ 5 k 2 5 2 ( 1 + k 2 ) + z 2 − ⋯ {\displaystyle \int_{0}^{\infty}{\textrm {sn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1}{1^{2}(1+k^{2})+z^{2}-{}}\,{\frac {1\cdot 2^{2}\cdot 3k^{2}}{3}(1+k^{2})+z^{2}-{},{\frac {3\cdot 4^{2}\cdot 5k^{2}}{5^{2}(1+k^{2})+z^{}}\cdots } z C { 0 } {\displaystyle z\in \mathbb {C} \setminus \{0\}, k 1 {\displaystyle 1}
∫ 0 ∞ sn 2 ( t ) e − t z d t = 2 z − 1 2 2 ( 1 + k 2 ) + z 2 − 2 ⋅ 3 2 ⋅ 4 k 2 4 2 ( 1 + k 2 ) + z 2 − 4 ⋅ 5 2 ⋅ 6 k 2 6 2 ( 1 + k 2 ) + z 2 − ⋯ {\displaystyle \int_{0}^{\infty}{\textrm {sn}}^{2}(t)e^{-tz}\,\mathrm {d} t={\frac {2z^{-1}}{2}(1+k^{2})+z^{2}-{}}\,{\frac {2\cdot 3^{2}\cdot 4k^{2}},{4^{2}(1+k^{2})+z^{2}-{},{\frac {4\cdot 5^{2}\cdot 6k^{2}}{6^{2}(1+k^{2})+z^{2}}\cdot } z C { 0 } {\displaystyle z\in \mathbb {C} \setminus \{0\}, k 1 {\displaystyle k 1}
∫ 0 ∞ cn ( t ) e − t z d t = 1 z + 1 2 z + 2 2 k 2 z + 3 2 z + 4 2 k 2 z + 5 2 z + ⋯ {\displaystyle \int _{0}^{\infty}{\textrm {cn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1^{2}}{z+{}}\,{\frac {1^{2}k^{2}}{z+{}}\,{\frac {3^{2}}{z+{}}\,{\frac {4^{2}k^{2}}{z+{}}\,{\frac {5^{2}}{z+{}}\,{\frac {5^{2}}}{cdots } z C 0 } {\displaystyle z\in \mathbb {C} \setminus \{0\}, k 1 {\displaystyle k 1}
∫ 0 ∞ dn ( t ) e − t z d t = 1 z + 1 2 k 2 z + 2 2 z + 3 2 k 2 z + 4 2 z + 5 2 k 2 z + ⋯ {\displaystyle \int _{0}^{\infty}{\textrm {dn}}(t)e^{-tz}\,\mathrm {d} t={\frac {1}{z+{}}\,{\frac {1^{2}}{z+{}}\,{\frac {2^{2}}{z+{}}\,{\frac {3^{2}k^{2}}{z+{}}\,{\frac {4^{2}}{z+{}}\,{\frac {5^{2}k^{2}}{z+{}}\cdots} z C {\displaystyle z\in \mathbb {C}} k 1 {\displaystyle 1} pg
∫ 0 ∞ sn ( t ) cn ( t ) dn ( t ) e − t z d t = 1 2 ⋅ 1 2 ( 2 − k 2 ) + z 2 − 1 ⋅ 2 2 ⋅ 3 k 4 2 ⋅ 3 2 ( 2 − k 2 ) + z 2 − 3 ⋅ 4 2 ⋅ 5 k 4 2 ⋅ 5 2 ( 2 − k 2 ) + z 2 − ⋯ {\displaystyle \int_{0}^{\infty}{\frac {{\textrm {sn}}(t){\textrm {cn}}}{\textrm {dn}}}e^{-tz}\,\mathrm {d}t={\frac {1}{2\cdot 1^{2}(2-k^{2})+z^{}\,{\frac {1\cdot 2^{2}\cdot 3^{4}{2-k^{2}}+z^{}\frac {3\cdot 4^{2}+z^{2}-{}},{\frac {3\cdot 4^{2}\cdot 5^{4}}{2\cdot 5^{2}(2-k^{2})+z^{}\cdots } 자코비 타원 함수의 역수는 역삼각형 함수 와 유사하게 정의될 수 있습니다. x sn ) {\displaystyle operatorname sn} (\xi )}, arcsn , m ) {\displaystyle \xi operatorname {arcsn} x,m)}. 타원 적분으로 나타낼 수 있으며 [32] [33] [34] [35] [3]
호를 ( x , m ) = ∫ 0 x d t ( 1 − t 2 ) ( 1 − m t 2 ) {\displaystyle \operatorname {arcsn}(x,m)=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(1-mt^{2}}}}}} 아크엔 ( x , m ) = ∫ x 1 d t ( 1 − t 2 ) ( 1 − m + m t 2 ) {\displaystyle \operatorname {arccn}(x,m)=\int _{x}^{1}{\frac {\mathrm {d}t}{\sqrt {(1-t^{2})(1-m+mt^{2}}}}} arcdn ( x , m ) = ∫ x 1 d t ( 1 − t 2 ) ( t 2 + m − 1 ) {\displaystyle \operatorname {arcdn}(x,m)=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(t^{2}+m-1) }}}} 지도투영 피어스 퀸큐셜 투영 은 자코비안 타원 함수를 기반으로 한 지도 투영 입니다.
참고 항목 메모들 ^ u R {\displaystyle u\in \mathbb {R}} m {\displaystyle m} ( 0 , 1 ] {\displaystyle [0,1]}( dn ( u , m ) {\displaystyle \operatorname {dn}(u,m)} 1 m sin 2 am ( u , m ) . {\displaystyle {\sqrt {1-m\sin^{2}\operatorname {am}(u,m)}(}).
참고문헌 Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 16" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .조나단 M. 보르바인, 피터 B. 보르바인: 파이랑 AGM. 해석적 수론과 계산 복잡도에 관한 연구 존 와일리 & 선즈, 1987. N. I. Akhiezer , 타원함수 이론의 요소들 (1970) Moscow, AMS 로 영어 번역 수학 모노그래프 79권 (1990) AMS, Road Island ISBN 0-8218-4532-2 A. C. 딕슨 타원함수의 기본적인 성질, 예를 들어 (Macmillan, 1894)알프레드 조지 그린힐 타원함수의 응용 (런던 , 뉴욕 , 맥밀런, 1892)에드먼드 T. 휘태커, 조지 네빌 왓슨: 현대 분석 과정. 4번째. 영국 캠브리지: 캠브리지 대학 출판부, 1990. S. 469–470. H. 핸콕 타원함수 이론 강의 (New York, J. Wiley &sons, 1910) Jacobi, C. G. J. (1829), Fundamenta nova theoriae functionum ellipticarum ISBN 978-1-108-05200-9 Reinhardt, William P.; Walker, Peter L. (2010), "Jacobian Elliptic Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 (프랑스어로) P. 소인 과 E.Lacour Principes de la théori des fonctions elliptiquetic set 응용 (Paris, Gauthier Villars, 1897) (프랑스어로) G. H. H. Halphen Traité des fonctions elliptique et deleurs applications (vol. 1) (Paris, Gauthier-Villars, 1886–1891)(프랑스어로) G. H. H. Halphen Traité des fonctions elliptique et deleurs applications (vol. 2) (Paris, Gauthier-Villars, 1886–1891)(프랑스어로) G. H. H. Halphen Traité des fonctions elliptique et deleurs applications (vol. 3) (Paris, Gauthier-Villars, 1886–1891)(프랑스어 로) J. 태너리와 J. 몰크 엘레망스 드 라테오리 데 폰션 타원체 . 나에게, 소개. 차이를 계산합니다. Irepartie (파리: Gauthier-Villarset fils, 1893)(프랑스어 로) J. 태너리와 J. 몰크 엘레망스 드 라테오리 데 폰션 타원체 . 토메 2, 계산 차이를 계산합니다. IIe party (파리: Gauthier-Villarset fils, 1893)(프랑스어 로) J. 태너리와 J. 몰크 엘레망스 드 라테오리 데 폰션 타원체 . 토메 3세, 정수를 계산합니다. 이 파티, 테오렘 제네로. 반전 (파리: 고티에-빌라르 세트 필름, 1893)(프랑스어 로) J. 태너리와 J. 몰크 엘레망스 드 라테오리 데 폰션 타원체 . 토메 IV, 정수를 계산합니다. IIe party, Applications (파리: Gauthier-Villarset fils, 1893)(프랑스어로) C.브리오와 J. C. 부케 Theorie des fonctions 타원형 (파리: Gauthier-Villars, 1875) 후쿠시마 도시오: 완전 타원 적분과 자코비안 타원 함수의 빠른 계산 . 2012, 일본 국립천문대 (国立天文台 )로완, 블랜치, 호렌스타인: 자코비안 타원 함수와 관련된 q계열의 반전에 대해 .황소. 아머. 수학.사회.48,1942 H. Ferguson, D.E. Nielsen, G. Cook: 세타 함수 놈의 정수 계수에 대한 분할 공식 . 계산의 수학, 29권, 숫자 131, Juli 1975 J. D. Fenton and R. S. Gardiner-Garden: 타원 적분 및 세타 및 타원 함수를 평가하기 위한 급속 수렴 방법 . J. 오스트레일리아의 수학. Soc. (시리즈B) 24, 1982, S. 57 아돌프 크네서: Neue Untersuchungeiner Reiheus der theory elliptischen Funktionen .J. Reine u. Angew. 수학. 157, 1927. 209쪽~218쪽 외부 링크 ^ p. Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions (First ed.). Cambridge University Press. ISBN 978-0-521-78078-0 ^ a b Walker, Peter (2003). "The Analyticity of Jacobian Functions with Respect to the Parameter k" . Proceedings of the Royal Society . 459 (2038): 2569–2574. Bibcode :2003RSPSA.459.2569W . doi :10.1098/rspa.2003.1157 . JSTOR 3560143 . S2CID 121368966 . ^ a b c d e Olver, F. W. J.; et al., eds. (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)" . National Institute of Standards and Technology. Retrieved 2018-02-26 . ^ "cplot, Python package for plotting complex-valued functions" . GitHub ^ a b c d e f Neville, Eric Harold (1944). Jacobian Elliptic Functions ^ a b Sala, Kenneth L. (November 1989). "Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean" . SIAM Journal on Mathematical Analysis . 20 (6): 1514–1528. doi :10.1137/0520100 . ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Carlson, B. C. (2010), "Elliptic Integrals" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Whittaker and Watson (1990) 페이지 469-470 ^ Alvaro H. Salas, Lorenzo J. H. Martinez, David L. R. Ocampo R. (2021-10-11), "Approximation of Elliptic Functions by Means of Trigonometric Functions with Applications", Mathematical Problems in Engineering , vol. 2021, pp. e5546666, doi :10.1155/2021/5546666 ISSN 1024-123X {{citation }}: CS1 유지 : 여러 이름 : 저자 목록 (링크 ) ^ "Table of Infinite Products Infinite Sums Infinite Series Elliptic Theta" . Retrieved 2021-08-31 .^ "A002103 - OEIS" . Retrieved 2023-05-28 .^ "Series Expansion of EllipticNomeQ differs from older Mathematica Version" . Retrieved 2023-05-28 .^ R. B. King, E. R. Canfield (1992-08-01), "Icosahedral symmetry and the quintic equation", Computers & Mathematics with Applications , vol. 24, no. 3, pp. 13–28, doi :10.1016/0898-1221(92)90210-9 ISSN 0898-1221 ^ Karl Heinrich Schellbach (1864), Die Lehre von den Elliptischen Integralen und den ThetaFunctionen , retrieved 2023-06-11 ^ Adolf Kneser (1927), "Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen." , Journal für die reine und angewandte Mathematik , vol. 158, pp. 209–218, ISSN 0075-4102 , retrieved 2023-06-11 ^ D. K. Lee (1989-03-01), Application of theta functions for numerical evaluation of complete elliptic integrals of the first and second kinds doi :10.2172/6137964 , OSTI 6137964 , retrieved 2023-06-11 ^ a b c d e f "Introduction to the Jacobi elliptic functions" . The Wolfram Functions Site . Wolfram Research, Inc. 2018. Retrieved January 7, 2018 .^ Whittaker, E.T. ; Watson, G.N. (1940). A Course in Modern Analysis ISBN 978-0-521-58807-2 ^ "Elliptic Functions: Complex Variables" .^ a b Viktor Prasolov and Yuri Soloviev (1997), "Elliptic Functions and Elliptic Integrals" (PDF) , arXiv: General Mathematics , retrieved 2023-06-24 ^ Weisstein, Eric W. "Jacobi Theta Functions" . MathWorld ^ Borwein, Jonathan M.; Borwein, Peter B. (1998). Pi and the AGM: a study in analytic number theory and computational complexity (PDF) . New York: Wiley. ISBN 978-0471315155 ^ "DLMF: 20.5 Infinite Products and Related Results" . Retrieved 2022-08-13 .^ Schett, Alois (1976). "Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions". Math. Comp . 30 (133): 143–147. doi :10.1090/S0025-5718-1976-0391477-3 . MR 0391477 . S2CID 120666361 . ^ Salzer, Herbert E. (July 1962). "Quick calculation of Jacobian elliptic functions" . Communications of the ACM . 5 (7): 399. doi :10.1145/368273.368573 S2CID 44953400 . ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ N.바기스. (2020) "야코비 타원함수 관련 계열 평가", preprint https://www.researchgate.net/publication/331370071_Evaluations_of_Series_Related_to_Jacobi_Elliptic_Functions ^ a b c d H.S. 월. (1948) "연속 분수에 대한 분석이론", 반 노스트랜드, 뉴욕 ^ 페론, O. (1957) 슈투트가르트, B.G. 테우브너, 밴드 2, 레레 폰 덴 케텐브루헨 ^ Reinhardt, W. P.; Walker, P. L. (2010), "§22.15 Inverse Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Ehrhardt, Wolfgang. "The AMath and DAMath Special Functions: Reference Manual and Implementation Notes" (PDF) . p. 42. Archived from the original (PDF) on 31 July 2016. Retrieved 17 July 2013 . ^ Byrd, P.F.; Friedman, M.D. (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2nd ed.). Berlin: Springer-Verlag. ^ Carlson, B. C. (2008). "Power series for inverse Jacobian elliptic functions" (PDF) . Mathematics of Computation . 77 (263): 1615–1621. Bibcode :2008MaCom..77.1615C . doi :10.1090/s0025-5718-07-02049-2 . Retrieved 17 July 2013 . 


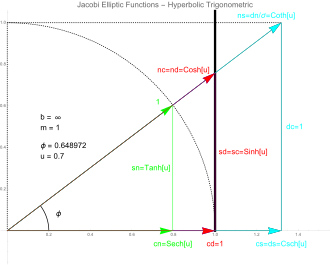










 한쪽 모서리에 형성한 직사각형인 "보조 직사각형"(일반적으로 평행사변형)을 검사하고, (
한쪽 모서리에 형성한 직사각형인 "보조 직사각형"(일반적으로 평행사변형)을 검사하고, ( 대각선으로 반대쪽 모서리인 "보조 직사각형"(일반적으로 평행사변형)을 검사하여 알 수 있습니다.그림에서와 같이 보조 사각형의 네 모서리는 원점에서 시계 반대 방향으로
대각선으로 반대쪽 모서리인 "보조 직사각형"(일반적으로 평행사변형)을 검사하여 알 수 있습니다.그림에서와 같이 보조 사각형의 네 모서리는 원점에서 시계 반대 방향으로 





 (가) 실제이고 보조 평행사변형은 실제로 직사각형이 되며 야코비 타원 함수는 모두 실제 선에서 실제 값이 됩니다.
(가) 실제이고 보조 평행사변형은 실제로 직사각형이 되며 야코비 타원 함수는 모두 실제 선에서 실제 값이 됩니다.




























![{\displaystyle u[\varphi ,k]={\frac {1}{\sqrt {1-k^{2}}}}\left({\frac {1+{\sqrt {1-k^{2}}}}{2}}\operatorname {E} \left(\varphi +\arctan \left({\sqrt {1-k^{2}}}\tan \varphi \right),{\frac {1-{\sqrt {1-k^{2}}}}{1+{\sqrt {1-k^{2}}}}}\right)-\operatorname {E} (\varphi ,k)+{\frac {k^{2}\sin \varphi \cos \varphi }{2{\sqrt {1-k^{2}\sin ^{2}\varphi }}}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/378f965ee3cc75264b4a54576250af91257e9231)





















![{\displaystyle {\begin{aligned}\operatorname {sn} (u;k)&=-{\frac {\vartheta _{00}[q(k)]\,\vartheta _{11}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\[7pt]\operatorname {cn} (u;k)&={\frac {\vartheta _{01}[q(k)]\,\vartheta _{10}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\[7pt]\operatorname {dn} (u;k)&={\frac {\vartheta _{01}[q(k)]\,\vartheta _{00}[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{00}[q(k)]\,\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6806c88afce87b86c875794c39e25fcb4e19ae7)
![{\displaystyle \vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c5acc090a4c8a2327974fa27125ca0f796ce535)
![{\displaystyle \vartheta _{01}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n-1}+w^{4n-2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05ceef12dd801305a4cf783265e8e157f4bdffde)
![{\displaystyle \vartheta _{10}(v;w)=2w^{1/4}\cos(v)\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n}+w^{4n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89a19ed41533c1761bf80ff54c7445c2518b5fe6)
![{\displaystyle \vartheta _{11}(v;w)=-2w^{1/4}\sin(v)\prod _{n=1}^{\infty }(1-w^{2n})[1-2\cos(2v)w^{2n}+w^{4n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92629da82416bb2f1c85e98624b798f5ef148eb)
![{\displaystyle {\begin{aligned}\operatorname {zn} (u;k)&={\frac {\pi }{2K}}{\frac {\vartheta _{01}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{01}[u\div {\bar {K}}(k);\,q(k)]}}\\&={\frac {\pi }{2K}}{\frac {\vartheta _{00}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{00}[u\div {\bar {K}}(k);\,q(k)]}}+k^{2}{\frac {\operatorname {sn} (u;k)\operatorname {cn} (u;k)}{\operatorname {dn} (u;k)}}\\&={\frac {\pi }{2K}}{\frac {\vartheta _{10}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{10}[u\div {\bar {K}}(k);\,q(k)]}}+{\frac {\operatorname {dn} (u;k)\operatorname {sn} (u;k)}{\operatorname {cn} (u;k)}}\\&={\frac {\pi }{2K}}{\frac {\vartheta _{11}'[u\div {\bar {K}}(k);\,q(k)]}{\vartheta _{11}[u\div {\bar {K}}(k);\,q(k)]}}-{\frac {\operatorname {cn} (u;k)\operatorname {dn} (u;k)}{\operatorname {sn} (u;k)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/920899581af5953dd66946736ebcf52a09a18b9a)



![{\displaystyle {\text{zn}}(u;k)=\sum _{n=1}^{\infty }{\frac {2\pi K(k)^{-1}\sin[\pi K(k)^{-1}u]q(k)^{2n-1}}{1-2\cos[\pi K(k)^{-1}u]q(k)^{2n-1}+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eac2343fdf578668c11bc7862154f8c4db46c85d)
![{\displaystyle \operatorname {sn} (u;k)={\frac {2\{\operatorname {zn} ({\tfrac {1}{2}}u;k)+\operatorname {zn} [K(k)-{\tfrac {1}{2}}u;k]\}}{k^{2}+\{\operatorname {zn} ({\tfrac {1}{2}}u;k)+\operatorname {zn} [K(k)-{\tfrac {1}{2}}u;k]\}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ce264e8ec4260c4bf9b81c19c20163f9d877a7b)

![{\displaystyle {\bar {q}}(\varepsilon )={\sqrt[{4}]{\varepsilon ^{-2}q(\varepsilon )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f2198727972192d1f89bd4961b72d7ca93cd1a)
![{\displaystyle \operatorname {sn} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\sin[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc87ae4bd16d376a53d099e8fcab4860db3418b6)
![{\displaystyle \operatorname {sn} (u;k)=2\,{\bar {q}}(k)\sin[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1-2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a328b02be9b321caa43ea402b97d0068a3ca5b6f)
![{\displaystyle \operatorname {cd} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {q(k)^{n-1}[1+q(k)^{2n-1}]}{1+2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db2690f90835fa4589e3e3174a0b2ab22ba80275)
![{\displaystyle \operatorname {cd} (u;k)=2\,{\bar {q}}(k)\cos[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1+2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/774f52fc2e1137e1f46efb463d797ab24aade95a)
![{\displaystyle \operatorname {cn} (u;k)=\,{\frac {4}{{\bar {K}}(k)}}\,{\bar {q}}(k)^{2}\cos[u\div {\bar {K}}(k)]\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}q(k)^{n-1}[1-q(k)^{2n-1}]}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0318250d65fdb7c97472344f089c7b07b10006)
![{\displaystyle \operatorname {cn} (u;k)=2\,{\sqrt[{4}]{1-k^{2}}}\,{\bar {q}}(k)\cos[u\div {\bar {K}}(k)]\prod _{n=1}^{\infty }{\frac {1+2q(k)^{2n}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n}}{1-2q(k)^{2n-1}\cos[2u\div {\bar {K}}(k)]+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90c0e6a7518eb6232e269a9f38f8ad21e4e2bcc6)
![{\displaystyle \operatorname {dn} (u;k)={\sqrt[{4}]{1-k^{2}}}\prod _{n=1}^{\infty }{\frac {1+2\cos[2u\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}{1-2\cos[2u\div {\bar {K}}(k)]q(k)^{2n-1}+q(k)^{4n-2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e6d604e0d59f04a5b68652c1fa1794388c9b909)
![{\displaystyle \operatorname {dn} (z;k)={\frac {\pi }{2K({\sqrt {1-k^{2}}})}}\sum _{n=-\infty }^{\infty }\operatorname {sech} {\bigl \{}\pi K({\sqrt {1-k^{2}}})^{-1}{\bigl [}K(k)n+{\tfrac {1}{2}}z{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cde2d3657222dba003ccad8dcdcdd2aac1007d2)
![{\displaystyle k'(\tau )={\sqrt {1-k^{2}}}={\biggl \{}{\vartheta _{01}[q(k)] \over \vartheta _{00}[q(k)]}{\biggr \}}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/575bf513613c0dcdfc250e96cd473755b97bc584)
![{\displaystyle q(k)=\exp {\biggl [}-\pi {\frac {K({\sqrt {1-k^{2}}})}{K(k)}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/024cce179f6fb6709a930647df3c2b6d0dcb6aea)

![{\displaystyle K(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{16^{a}(a!)^{4}}}k^{2a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ea0da33be9e1a79cff559e92a2acab4b6702c0)
![{\displaystyle {\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}={\frac {\vartheta _{00}[q(k)]-\vartheta _{01}[q(k)]}{\vartheta _{00}[q(k)]+\vartheta _{01}[q(k)]}}={\biggl [}\sum _{n=1}^{\infty }2\,q(k)^{(2n-1)^{2}}{\biggr ]}{\biggl [}1+\sum _{n=1}^{\infty }2\,q(k)^{4n^{2}}{\biggr ]}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e6e9f89499cbd8586d2bfb94cac37ac1406caaa)

![{\displaystyle q(k)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}{\biggr )}^{4n-3}=k^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{\biggr ]}{\biggr \}}^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86f60c0189474eb87cf741c03c5fd0b8d52939d1)










![{\displaystyle \mathrm {Sc} (4)={\frac {2}{3}}\sum _{m=1}^{3}\mathrm {Sc} (m)\,\mathrm {Kn} (4-m)={\frac {2}{3}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c0e2f6c8f1e9bd5a3f5eb70920b4d90fff4bc48)

![{\displaystyle \mathrm {Sc} (5)={\frac {2}{4}}\sum _{m=1}^{4}\mathrm {Sc} (m)\,\mathrm {Kn} (5-m)={\frac {2}{4}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bb6c5b6b9b4e5d44f245fc6b05b5e3b5ddb4b25)

![{\displaystyle \mathrm {Sc} (6)={\frac {2}{5}}\sum _{m=1}^{5}\mathrm {Sc} (m)\,\mathrm {Kn} (6-m)={\frac {2}{5}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (5)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (5)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1331a9d6e16d802ebaf5eb68d2d9724296a7f64)

![{\displaystyle q(x)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-x^{2}}}}{1+{\sqrt[{4}]{1-x^{2}}}}}{\biggr )}^{4n-3}=x^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}x^{2n}{\biggr ]}{\biggr \}}^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21eefe073b61084357f786b098eedee8400cd99a)



 (는) 사용되지 않습니다.)
(는) 사용되지 않습니다.) (가) 억제됨)
(가) 억제됨)



























 매개 변수
매개 변수 








![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt[{4}]{12}}-{\sqrt {3}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1fdc364c7e2f75dc1bc3262ad9d966b0a814f3e)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt {3}}-{\sqrt[{4}]{12}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aefdbe27221987f0946aabfc59783374b0c3685f)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {1}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666075f03e66bd7431da52da947bbe89ec0e65d3)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{3}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}({\sqrt[{4}]{27}}+{\sqrt[{4}]{3}}-{\sqrt {2}}){\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8980bd4033a33c16c15ae4db9171ac26aaab380d)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {1}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\bigl [}\tan({\tfrac {1}{5}}\pi )+1-{\sqrt {2\tan({\tfrac {3}{20}}\pi )}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e82ae23aa671181f00e7b128c13f5d9474a48d72)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {3}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\bigl [}\tan({\tfrac {1}{5}}\pi )-1+{\sqrt {2\cot({\tfrac {3}{20}}\pi )}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75820cbad7574dd85340af3606cd5b49ef9346f1)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\bigl [}\cot({\tfrac {1}{10}}\pi )-1-{\sqrt {2\tan({\tfrac {1}{20}}\pi )}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd7da1e4920ab7f51ccdb4e6cf9c2da377b1359b)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\bigl [}\cot({\tfrac {1}{10}}\pi )+1-{\sqrt {2\cot({\tfrac {1}{20}}\pi )}}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/631ce1bb4c8c0265b87cb69894a7a3b0888f2a3b)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {1}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=2{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {3}{20}}\pi )\cos({\tfrac {1}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78b9460db91bf4414d907524302ebf4aed1e8092)
![{\displaystyle \operatorname {cn} {\bigl [}{\tfrac {3}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=2{\sqrt[{4}]{{\sqrt {5}}-2}}\,{\sqrt {\sin({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2773939d14ee3ffa03eb1e084583776e08132ee)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\tan({\tfrac {1}{20}}\pi )}}\,({\sqrt {\cot({\tfrac {1}{10}}\pi )+1}}-{\sqrt {\cot({\tfrac {1}{10}}\pi )-3}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5f0cf3ac1b607395cabad28334c3e7648f45afe)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}={\tfrac {1}{2}}{\sqrt[{4}]{2\cot({\tfrac {1}{20}}\pi )}}\,({\sqrt {\cot({\tfrac {1}{10}}\pi )+3}}-{\sqrt {\cot({\tfrac {1}{10}}\pi )-1}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120ded864367f3cf8e24a6cc1d64c3da6735d60b)
![{\displaystyle \operatorname {cn} [{\tfrac {2}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb0eb2415db79a3ac708a4bb79dc4870a84e9304)
![{\displaystyle \operatorname {cn} [{\tfrac {4}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7d11135f13c75bfe3073d59e143d4129565baa0)
![{\displaystyle \operatorname {cn} [{\tfrac {6}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\tanh {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e093f3ab9ac45bfb41dcbb5e339f0df1a337b54d)
![{\displaystyle \operatorname {sn} [{\tfrac {2}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\sin({\tfrac {1}{7}}\pi )\cot({\tfrac {3}{28}}\pi )}}+\sin({\tfrac {1}{14}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72868376532441a20c25a7c1f916e5eebc77a011)
![{\displaystyle \operatorname {sn} [{\tfrac {4}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {1}{14}}\pi )\tan({\tfrac {5}{28}}\pi )}}+\sin({\tfrac {3}{14}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0523ef6204b4638873f74d31e3aa0aa564b1ed31)
![{\displaystyle \operatorname {sn} [{\tfrac {6}{7}}K({\tfrac {1}{2}}{\sqrt {2}});{\tfrac {1}{2}}{\sqrt {2}}]=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}{\sqrt {2\cos({\tfrac {3}{14}}\pi )\cot({\tfrac {1}{28}}\pi )}}+\cos({\tfrac {1}{7}}\pi ){\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b48e0da65be123b510690c72203f8af647331e7b)


![{\displaystyle \operatorname {cn} \{{\tfrac {2}{5}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi )\}=\tan {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}}\tan({\tfrac {1}{10}}\pi )+{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr ]}-{\tfrac {1}{12}}\pi {\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/933a02326482fbf08fef7ab17eddc278ae7808a2)
![{\displaystyle \operatorname {cn} \{{\tfrac {4}{5}}K{\bigl [}\sin({\tfrac {1}{12}}\pi ){\bigr ]};\sin({\tfrac {1}{12}}\pi )\}=\tan {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}}\tan({\tfrac {1}{10}}\pi )-{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr ]}+{\tfrac {1}{12}}\pi {\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4fb56fad7eb5017f3be857a1b3e0574c05ca45)
![{\displaystyle \operatorname {cn} \{{\tfrac {2}{5}}K{\bigl [}\cos({\tfrac {1}{12}}\pi ){\bigr ]};\cos({\tfrac {1}{12}}\pi )\}=\cot {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}}\cot({\tfrac {1}{5}}\pi )+{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr ]}-{\tfrac {1}{12}}\pi {\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21eff3a94fefa8cd1ee6dce53cffcb4155f86797)
![{\displaystyle \operatorname {cn} \{{\tfrac {4}{5}}K{\bigl [}\cos({\tfrac {1}{12}}\pi ){\bigr ]};\cos({\tfrac {1}{12}}\pi )\}=\cot {\bigl \{}\arctan {\bigl [}{\sqrt[{3}]{10}}\cot({\tfrac {1}{5}}\pi )-{\tfrac {1}{3}}{\sqrt {3}}({\sqrt[{3}]{10}}-1){\bigr ]}+{\tfrac {1}{12}}\pi {\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fb887459197ae8a7fe0eed1a3e295a58588c706)



























![{\displaystyle {\begin{aligned}\operatorname {sn} (x+y;k)&={\operatorname {sn} (x;k)\operatorname {cn} (y;k)\operatorname {dn} (y;k)+\operatorname {sn} (y;k)\operatorname {cn} (x;k)\operatorname {dn} (x;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}},\\[8pt]\operatorname {cn} (x+y;k)&={\operatorname {cn} (x;k)\operatorname {cn} (y;k)-\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {dn} (x;k)\operatorname {dn} (y;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}},\\[8pt]\operatorname {dn} (x+y;k)&={\operatorname {dn} (x;k)\operatorname {dn} (y;k)-k^{2}\operatorname {sn} (x;k)\operatorname {sn} (y;k)\operatorname {cn} (x;k)\operatorname {cn} (y;k) \over {1-k^{2}\operatorname {sn} ^{2}(x;k)\operatorname {sn} ^{2}(y;k)}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a1fe383a53d9073f8a5bde16e438abfa4f4c0f)












![{\displaystyle \operatorname {sn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {\sqrt {2}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed82907c77897c29b197ad49d191e97568af3a0f)
![{\displaystyle \operatorname {cn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {{\sqrt {2}}\,{\sqrt[{4}]{1-k^{2}}}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3438731cb1b1b39124a6e4675420fb84a8e89bba)
![{\displaystyle \operatorname {dn} \left[{\tfrac {1}{2}}K(k);k\right]={\sqrt[{4}]{1-k^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5257c49ceccef91f2fca3a910e76ee9b0271e33)

![{\displaystyle s=\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d02d4647e1efcb10a29246750edb36cd609ebdd)
![{\displaystyle \operatorname {cn} \left[{\tfrac {2}{3}}K(k);k\right]=1-\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ff147f7bba74210bfc2aecb6a7d5f1e631e593)
![{\displaystyle \operatorname {dn} \left[{\tfrac {2}{3}}K(k);k\right]=1/\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e954723c754da74da208796a92de7a6f1c12ee3)
![{\displaystyle \operatorname {sn} {\biggl \langle }{\frac {1}{3}}K{\bigl \{}\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}{\bigr \}};\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}{\biggr \rangle }=\tanh {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e199fe6311c6d0e5ff95d17e03c4640217acec42)
![{\displaystyle \operatorname {cn} {\biggl \langle }{\frac {1}{3}}K{\bigl \{}\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}{\bigr \}};\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}{\biggr \rangle }=\operatorname {sech} {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4cde4a4f16a7755a64397f2202ad146f3a20d0)
![{\displaystyle {\frac {1}{2}}{\sqrt {2}}=\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt {2}}\,)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c95b922fd46dc29f836c8bff179b5d55a320d3)
![{\displaystyle \operatorname {sn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}\,{\bigr )};{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\tanh {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt[{4}]{12}}+{\sqrt {3}}{\bigr )}{\bigr ]}={\frac {1}{2}}({\sqrt[{4}]{12}}-{\sqrt {3}}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3762e86af9f156ab8c2900432aa707544120d74)
![{\displaystyle \operatorname {cn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}\,{\bigr )};{\frac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt[{4}]{12}}+{\sqrt {3}}{\bigr )}{\bigr ]}={\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce2df85430b691b517d760b987422d69a41fa522)
![{\displaystyle {\frac {1}{2}}=\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt[{3}]{4/3}}\,)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/962b614f2fb85952b74317b8864c90d5db9c2a02)
![{\displaystyle \operatorname {sn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}}{\bigr )};{\frac {1}{2}}{\bigr ]}=\tanh {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {({\tfrac {4}{3}})^{4/3}-({\tfrac {4}{3}})^{2/3}+1}}-({\tfrac {4}{3}})^{2/3}+2}}+{\sqrt {({\tfrac {4}{3}})^{2/3}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abe4f0b9d59c430d868fa4019907f9175dff23ff)
![{\displaystyle \operatorname {cn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{2}}{\bigr )};{\frac {1}{2}}{\bigr ]}=\operatorname {sech} {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {({\tfrac {4}{3}})^{4/3}-({\tfrac {4}{3}})^{2/3}+1}}-({\tfrac {4}{3}})^{2/3}+2}}+{\sqrt {({\tfrac {4}{3}})^{2/3}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24e00daf124f0ac76d1aa08188e5bc02ea8c62c)
![{\displaystyle {\frac {1}{4}}=\tan {\bigl [}{\frac {1}{2}}\arctan {\bigl (}x^{3}{\bigr )}{\bigr ]}(x={\sqrt[{3}]{8/15}}\,)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbd88acfcc2ac3c715d94a0c4c7b445b5934430d)
![{\displaystyle \operatorname {sn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{4}}{\bigr )};{\frac {1}{4}}{\bigr ]}=\tanh {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {({\tfrac {8}{15}})^{4/3}-({\tfrac {8}{15}})^{2/3}+1}}-({\tfrac {8}{15}})^{2/3}+2}}+{\sqrt {({\tfrac {8}{15}})^{2/3}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87742a0e40658e1d84956738c686fb38e0dc72a8)
![{\displaystyle \operatorname {cn} {\bigl [}{\frac {1}{3}}K{\bigl (}{\frac {1}{4}}{\bigr )};{\frac {1}{4}}{\bigr ]}=\operatorname {sech} {\bigl [}{\frac {1}{2}}\ln {\bigl (}{\sqrt {2{\sqrt {({\tfrac {8}{15}})^{4/3}-({\tfrac {8}{15}})^{2/3}+1}}-({\tfrac {8}{15}})^{2/3}+2}}+{\sqrt {({\tfrac {8}{15}})^{2/3}+1}}{\bigr )}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d818f9267c3a0888cddb141667399758d7c7916)

![{\displaystyle t={\frac {1}{2}}-{\frac {1}{2}}k^{2}\operatorname {sn} \left[{\tfrac {2}{5}}K(k);k\right]^{2}\operatorname {sn} \left[{\tfrac {4}{5}}K(k);k\right]^{2}={\frac {\operatorname {sn} \left[{\frac {4}{5}}K(k);k\right]^{2}-\operatorname {sn} \left[{\frac {2}{5}}K(k);k\right]^{2}}{2\operatorname {sn} \left[{\frac {2}{5}}K(k);k\right]\operatorname {sn} \left[{\frac {4}{5}}K(k);k\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6faeb0bd443aec59f475154cd2e06eab433dc53e)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K(k);k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1-t{\sqrt {t^{2}+1}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6bef39ba69546de008e628b153b9ce90be21ff5)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K(k);k{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1+t{\sqrt {t^{2}+1}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8949959718e47f0d0d8b7cf5d9934406079dce99)

![{\displaystyle t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5275ee0253781ce560ab97354cadb3d37ec704e)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1-t{\sqrt {t^{2}+1}})}}\,{\bigl [}k={\tfrac {1}{2}}{\sqrt {2}}\,\cap \,t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e0cf6640df391ad4ce40ddc364f281659e355c)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=(1+k^{2})^{-1/2}{\sqrt {2(1-t-t^{2})(t^{2}+1+t{\sqrt {t^{2}+1}})}}\,{\bigl [}k={\tfrac {1}{2}}{\sqrt {2}}\,\cap \,t={\tfrac {1}{4}}({\sqrt {5}}+1)({\sqrt[{4}]{5}}-1){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed0ced0688915ff3c6713dc9795b798576089853)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {2}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}\cot {\bigl (}{\tfrac {1}{10}}\pi {\bigr )}-{\tfrac {1}{2}}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e1ee26bd9509ed87601cc87952305c57ac00f3b)
![{\displaystyle \operatorname {sn} {\bigl [}{\tfrac {4}{5}}K({\tfrac {1}{2}}{\sqrt {2}}\,);{\tfrac {1}{2}}{\sqrt {2}}\,{\bigr ]}=\operatorname {sech} {\bigl \{}{\tfrac {1}{2}}\operatorname {arcoth} {\bigl [}{\tfrac {1}{2}}\cot {\bigl (}{\tfrac {1}{10}}\pi {\bigr )}+{\tfrac {1}{2}}{\bigr ]}{\bigr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ad2224cc48ec1df3d7ac03d1ec3b14fd6f49acc)










![{\displaystyle \operatorname {sc} [{\tfrac {2}{3}}K(k);k]={\frac {{\sqrt {3}}\,\vartheta _{01}[q(k)^{6}]}{{\sqrt {1-k^{2}}}\,\vartheta _{01}[q(k)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d48eb0ba8be378538574990cf6d98f0f6837ec5)
![{\displaystyle \operatorname {sn} [{\tfrac {1}{3}}K(k);k]={\frac {2\,\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {3\,\vartheta _{01}[q(k)^{3}]^{2}-\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b5a3ba0ecfd3bcc33e24df1a5e4cab495e2a817)
![{\displaystyle \operatorname {cn} [{\tfrac {2}{3}}K(k);k]={\frac {3\,\vartheta _{00}[q(k)^{3}]^{2}-\vartheta _{00}[q(k)]^{2}}{3\,\vartheta _{00}[q(k)^{3}]^{2}+\vartheta _{00}[q(k)]^{2}}}={\frac {2\,\vartheta _{01}[q(k)]^{2}}{3\,\vartheta _{01}[q(k)^{3}]^{2}+\vartheta _{01}[q(k)]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d5c60f61392e4e9b9df28d42df2570ad12e0e67)
![{\displaystyle \operatorname {sn} [{\tfrac {1}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/488e8915c07e6ee03f05f26481954bd07f528779)
![{\displaystyle \operatorname {sn} [{\tfrac {3}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{01}[q(k)^{5}]}{\vartheta _{01}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c799d150dd580ad0f8bb830fbd2b8bb11da1e2ec)
![{\displaystyle \operatorname {cn} [{\tfrac {2}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}+1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0c2a98347634656f4c080e7c5cabcf3fcd237fd)
![{\displaystyle \operatorname {cn} [{\tfrac {4}{5}}K(k);k]={\biggl \{}{\frac {{\sqrt {5}}\,\vartheta _{00}[q(k)^{5}]}{\vartheta _{00}[q(k)]}}-1{\biggr \}}{\biggl \{}{\frac {5\,\vartheta _{01}[q(k)^{10}]^{2}}{\vartheta _{01}[q(k)^{2}]^{2}}}-1{\biggr \}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9661704fd91af89a6f6f3196aed7fe2d2e4893af)




















 m
m




![{\displaystyle {\begin{aligned}&{\frac {{\textrm {dn}}\left((p/2-a)\tau K\left[{\frac {p\tau }{2}}\right];k\left({\frac {p\tau }{2}}\right)\right)}{\sqrt {k'\left({\frac {p\tau }{2}}\right)}}}={\frac {\sum _{n=-\infty }^{\infty }q^{p/2n^{2}+(p/2-a)n}}{\sum _{n=-\infty }^{\infty }(-1)^{n}q^{p/2n^{2}+(p/2-a)n}}}\\[4pt]={}&-1+{\frac {2}{1-{}}}\,{\frac {q^{a}+q^{p-a}}{1-q^{p}+{}}}\,{\frac {(q^{a}+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}}}\,{\frac {q^{p}(q^{a}+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}}}\,{\frac {q^{2p}(q^{a}+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}}\cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef2c799ca80eecd7e2fdb629c2148326e37c57d)












