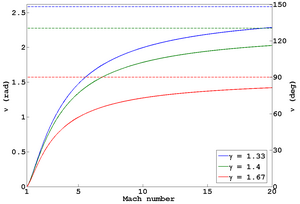
함수(M {\displaystyle  )와 마하 번호( displaystyle
)와 마하 번호( displaystyle  및 특정 열 용량의 비율
및 특정 열 용량의 비율 의 변동.파선은 마하 수가 무한대로 증가함에 따라
의 변동.파선은 마하 수가 무한대로 증가함에 따라 제한 값 을 나타낸다.
제한 값 을 나타낸다. 공기역학에서 Prandtl-Meyer 함수는 흐름이 소닉 속도(M=1)에서 1보다 큰 마하(M) 숫자로 등전적으로 변하는 각도를 설명한다.소닉(M = 1) 흐름이 볼록한 모서리를 회전할 수 있는 최대 각도는 M = {\ \에 대해 계산한다 이상적인 기체는 다음과 같이 표현된다.
이상적인 기체는 다음과 같이 표현된다.
![{\displaystyle {\begin{aligned}\nu (M)&=\int {\frac {\sqrt {M^{2}-1}}{1+{\frac {\gamma -1}{2}}M^{2}}}{\frac {\,dM}{M}}\\[4pt]&={\sqrt {\frac {\gamma +1}{\gamma -1}}}\cdot \arctan {\sqrt {{\frac {\gamma -1}{\gamma +1}}(M^{2}-1)}}-\arctan {\sqrt {M^{2}-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9274b6a4ca1b46bff29be98aacca4268665e001c)
여기서 은 (는) Prandtl-Meyer 함수, 은
(는) Prandtl-Meyer 함수, 은 (는) 흐름의 마하 수, 은
(는) 흐름의 마하 수, 은 (는) 특정 열 용량의 비율이다.
(는) 특정 열 용량의 비율이다.
관례에 따라 ( 1) = 과 같은 통합 상수가 선택된다.
마하 숫자는 1에서 까지 다양하므로  \,}은(는) 에서 최대 까지의 값을
\,}은(는) 에서 최대 까지의 값을 취한다
취한다

| 등방성 팽창의 경우, |  |
| 등방성 압축의 경우, |  |
여기서, 은 흐름이 회전하는 각도의 절대값이며, M}은
흐름이 회전하는 각도의 절대값이며, M}은 흐름 마하 수이며 접미사 "1"과 "2"는 각각 초기 조건과 최종 조건을 나타낸다.
흐름 마하 수이며 접미사 "1"과 "2"는 각각 초기 조건과 최종 조건을 나타낸다.
참고 항목
참조






![{\displaystyle {\begin{aligned}\nu (M)&=\int {\frac {\sqrt {M^{2}-1}}{1+{\frac {\gamma -1}{2}}M^{2}}}{\frac {\,dM}{M}}\\[4pt]&={\sqrt {\frac {\gamma +1}{\gamma -1}}}\cdot \arctan {\sqrt {{\frac {\gamma -1}{\gamma +1}}(M^{2}-1)}}-\arctan {\sqrt {M^{2}-1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9274b6a4ca1b46bff29be98aacca4268665e001c)
 (는) Prandtl-Meyer 함수,
(는) Prandtl-Meyer 함수, 



 흐름이 회전하는 각도의 절대값이며,
흐름이 회전하는 각도의 절대값이며, 
