회전

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '회전'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2014년 3월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

회전은 물체가 시계방향 또는 시계반대방향으로 회전축을 중심으로 원을 그리며 움직이는 것입니다.3차원 물체는 무한대의 회전축을 가질 수 있다.

회전축이 몸 자체의 질량 중심을 내부적으로 통과하면 몸은 자동 회전 또는 회전하고 있으며, 축의 표면 교점은 극이라고 할 수 있다.태양 주위의 행성 지구와 같이 완전히 외부 축을 중심으로 한 회전은 일반적으로 중력에 의해 생성될 때 회전 또는 공전이라고 하며 회전 축의 끝은 궤도 극이라고 할 수 있습니다.

수학

수학적으로 회전은 번역과 달리 점을 고정시키는 강체 운동이다.이 정의는 2차원 및 3차원(각각 평면 내 및 공간 내)에서의 회전에 적용됩니다.

모든 강체 이동은 회전, 변환 또는 둘의 조합입니다.

회전은 단순히 공통점에 대한 점진적인 반지름 방향입니다.그 공통점은 그 움직임의 축 안에 있다.축은 움직임의 평면에 대해 90도 수직입니다.

점 또는 축을 중심으로 회전한 후 동일한 점/축을 중심으로 두 번째 회전을 수행하면 세 번째 회전이 발생합니다.회전의 역방향(역방향)도 회전입니다.따라서 점/축 주위의 회전은 그룹을 형성합니다.그러나 점 또는 축을 중심으로 회전하고 다른 점/축을 중심으로 회전하면 변환과 같은 회전 이외의 결과가 발생할 수 있습니다.

x, y 및 z 축 주위의 회전을 주 회전이라고 합니다.모든 축을 중심으로 회전하려면 x 축을 중심으로 회전한 후 y 축을 중심으로 회전한 다음 z 축을 중심으로 회전합니다.즉, 모든 공간 회전이 주 회전의 조합으로 분해될 수 있습니다.

비행 역학에서 주요 회전은 요, 피치 및 롤(Tait-Bryan 각도)로 알려져 있습니다.이 용어는 컴퓨터 그래픽스에서도 사용됩니다.

천문학

천문학에서 회전은 흔히 관찰되는 현상이다.별, 행성, 그리고 이와 유사한 물체들은 모두 축을 중심으로 회전한다.태양계 행성의 자전 속도는 시각적인 특징을 추적함으로써 처음 측정되었다.별의 자전은 도플러 이동 또는 활성 표면 특징을 추적하여 측정됩니다.

이 회전은 지구의 기준 프레임에 원심 가속을 유발하여 적도에 가까운 중력의 영향을 약간 상쇄시킵니다.지구의 중력은 두 가지 질량 효과를 결합하여 물체가 극지방보다 적도에서 약간 덜 무게가 나간다.또 다른 이유는 시간이 지나면서 지구가 약간 타원형 구형으로 변형된다는 것입니다; 비슷한 적도 팽대부가 다른 행성에도 생겨납니다.

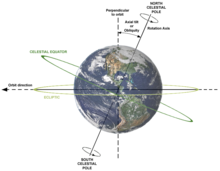
행성 회전의 또 다른 결과는 세차 운동 현상이다.자이로스코프처럼, 전체적인 효과는 행성의 축 이동에서 약간의 "흔들림"이다.현재 지구축의 궤도면 기울기는 23.44도이지만(황도의 기울기) 이 각도는 천천히 변화한다(수천년에 걸쳐).(분점과 북극성의 세차 운동을 참조하십시오.)

혁명

회전은 회전의 동의어로 종종 사용되는 반면, 많은 분야, 특히 천문학 및 관련 분야에서는, 한 물체가 다른 물체의 주위를 이동할 때 종종 궤도 회전으로 언급되는 회전은 축 주위의 움직임을 의미하기 위해 사용된다.달은 행성 주위를 돌고, 행성은 별 주위를 돌고, 별들은 은하 중심 주위를 천천히 돈다.은하 구성 요소의 움직임은 복잡하지만 일반적으로 회전 구성 요소를 포함합니다.

역회전

지구를 포함한 태양계의 대부분의 행성들은 태양 주위를 도는 것과 같은 방향으로 회전한다.금성과 천왕성은 예외이다.금성은 천천히 뒤로 회전하는 것으로 생각될 수 있다.천왕성은 궤도에 비해 거의 옆으로 회전한다.현재 추측으로는 천왕성은 전형적인 순행 방향에서 출발하여 역사 초기에 큰 충돌로 인해 옆으로 넘어졌을 것으로 추측된다.왜소행성 명왕성은 옆으로 회전한다는 점 등 여러 가지 점에서 특이하다.

물리

회전 속도는 각 주파수(rad/s) 또는 주파수(시간당 회전 수) 또는 주기(초, 일 등)로 지정됩니다.각 주파수의 시간 변화율은 토크에 의해 발생하는 각 가속도(rad/s²)입니다.둘의 비율(회전 시작, 정지 또는 기타 변경 시 무게)은 관성 모멘트에 의해 결정됩니다.

각속도 벡터(축방향 벡터)는 회전축의 방향도 나타냅니다.마찬가지로 토크는 축방향 벡터입니다.

고정 축을 중심으로 한 회전의 물리학은 회전의 축-각도 표현으로 수학적으로 설명된다.이 오른손 법칙에 따르면 관찰자로부터 멀어지는 방향은 시계방향 회전에, 반대방향 회전에 의한 관찰자 방향은 나사처럼 대응된다.

우주론적 원리

물리 법칙은 현재 어떤 고정 회전에서도 불변하는 것으로 여겨진다. (비록 회전하는 관점에서 보면 변하는 것처럼 보이지만: 회전하는 기준 틀 참조)

현대 물리 우주론에서, 우주론적 원리는 충분히 큰 규모로 볼 때 우주의 물질의 분포가 균질하고 등방적이라는 개념이다, 왜냐하면 힘은 우주 전체에 걸쳐 균일하게 작용하고 선호되는 방향이 없기 때문에, 따라서, 관찰할 수 있는 불규칙성을 만들어내지 않아야 하기 때문이다.n 빅뱅이 초기에 설정한 물질 분야의 진화 과정에 걸친 대규모 구조.

특히, 공간에서의 방향에 관계없이 동일하게 동작하는 시스템의 경우, 라그랑지안은 회전 불변합니다.노에터의 정리에 따르면, 만약 물리계의 작용(시간 경과에 따른 라그랑지안의 적분)이 회전 중에 변하지 않는다면, 각운동량은 보존된다.

오일러 회전

오일러 회전은 회전에 대한 다른 설명을 제공합니다.이것은 오일러 각도 중 하나를 바꾸고 다른 두 개의 각도를 일정하게 유지함으로써 얻어진 운동으로 정의된 세 개의 회전의 구성이다.오일러 회전은 외부 프레임이나 함께 움직이는 회전체 프레임으로 표현되지 않고 혼합된 형태로 표현됩니다.이들은 혼재된 회전 시스템을 구성하는데, 첫 번째 각도는 외부 축 z를 중심으로 노드 라인을 이동하고, 두 번째 각도는 노드 라인을 중심으로 회전하며, 세 번째 각도는 움직이는 체내에 고정된 축을 중심으로 한 고유 회전입니다.

이러한 회전을 세차운동, 교락 및 고유 회전이라고 합니다.

비행 역학

비행 역학에서 위의 오일러 각도로 설명된 주요 회전을 피치, 롤링 및 요라고 합니다.회전이라는 용어는 항공기에서 특히 이륙 후 상승 출발할 때 항공기의 상승 피치(노즈 이동)를 지칭하기 위해 사용된다.

주 회전은 짐벌 및 조이스틱과 같은 여러 물리적 시스템을 모델링할 수 있는 장점이 있으므로 쉽게 시각화할 수 있으며 회전을 저장하는 매우 작은 방법입니다.그러나 회전 조합과 같은 간단한 작업도 비용이 많이 들고 특정 회전의 각도를 고유하게 계산할 수 없는 짐벌 잠금 형태에 시달리기 때문에 계산에 사용하기 어렵습니다.

놀이 기구

많은 놀이 기구들이 회전을 제공합니다.관람차는 중력 또는 기계적으로 회전하는 각 곤돌라마다 수평 중심축과 평행축을 가진다.그 결과, 곤돌라의 방향은 항상 직립(회전하지 않음)하고, 단지 번역됩니다.변환 벡터의 끝은 원을 나타냅니다.회전목마는 수직축을 중심으로 회전합니다.많은 놀이기구가 여러 축을 중심으로 회전하는 조합을 제공합니다.Chair-O-Plane에서 수직 축에 대한 회전은 기계적으로 제공되며, 수평 축에 대한 회전은 구심력에 의한 것이다.롤러코스터 역방향에서 수평축에 대한 회전은 관성이 사람들을 자리에 있게 하는 하나 이상의 전체 주기입니다.

스포츠

보통 스핀이라고 불리는 공이나 다른 물체의 회전은 테니스, 영국, 당구와 풀장에서의 탑스핀과 백스핀, 야구에서의 커브볼, 크리켓에서의 스핀볼링, 플라잉디스크 스포츠 등을 포함한 많은 스포츠에서 역할을 한다.탁구 패들은 플레이어가 공에 많든 적든 회전량을 부여할 수 있도록 다른 표면 특성을 가지고 제조된다.

선수가 세로축을 중심으로 1회 이상 회전하는 것을 피겨스케이팅에서는 스핀, 바톤 회전에서는 바톤 회전, 스노보드 등에서는 360, 540, 720 등으로 부른다.선수나 연주자가 수평축을 중심으로 1회 이상 회전하는 것을 체조, 수상스키, 기타 많은 스포츠에서는 플립, 롤, 공중제비, 헬리 등이라고 하며, 다이빙에서는 1.5, 2.5, 게인(물로부터 멀어지는 방향)이라고 한다.수직 회전과 수평 회전의 조합(360°의 백 플립)수상스키 프리스타일 점프에서는 뫼비우스라고 불린다.

일반적으로 180도에서 360도 사이의 수직 축을 중심으로 하는 플레이어의 회전을 스핀 무브라고 부를 수 있으며, 기만 또는 회피 기교, 또는 공이나 퍽 등을 플레이, 패스 또는 수신하려는 시도 또는 골이나 다른 플레이어의 시야를 제공하기 위해 사용됩니다.하키, 농구, 다양한 코드의 축구, 테니스 등에서 자주 볼 수 있다.

고정축 대 고정점

고정된 점을 중심으로 한 물체의 회전 시퀀스의 최종 결과는 항상 축을 중심으로 한 회전과 동일합니다.그러나 물체는 둘 이상의 축에서 동시에 고정점을 중심으로 물리적으로 3D로 회전할 수 있으며, 이 경우 고정점만 있는 단일 고정 회전 축이 없습니다.그러나 이러한 두 가지 설명은 조정될 수 있습니다. 이러한 물리적 움직임은 물체에 대한 축의 방향이 시시각각 변경될 수 있는 경우 항상 단일 회전 축의 관점에서 다시 기술될 수 있습니다.

2차원 회전축

2차원 회전은 3차원 회전과 달리 회전 축이 없습니다.이것은 선형 변환의 경우, 2차원 회전에 의해 변하지 않는 방향은 물론 동일성을 제외하고 존재하지 않는다는 것과 같습니다.

이러한 방향의 존재에 대한 질문은 회전을 나타내는 행렬 A에 대한 고유 벡터의 존재에 대한 질문이다.원점을 중심으로 시계 반대 방향으로 각도$\theta {\displaystyle }$(\$displaystyle \theta)$를 통해 2D 회전할 때마다 다음과 같은 행렬로 간단하게 나타낼 수 있습니다.

$(\displaystyle A=bmatrix\cos \theta &-\sin \theta &\cos \theta \end {bmatrix})$

표준 고유값 결정은 특성 방정식으로 이어집니다.

${\displaystyle {\lambda \mathrm{}}^{}2}$ - ${\displaystyle 2}$ ${\displaystyle \mathrm{\lambda }}$ cos${\displaystyle }$ + 1$=$ $0$ \$displaystyle$ \$displayda$^ {$2$} - $2$\ $cos$ \$theta$+ 1$=$0 ,

가지고 있다

$(\displaystyle\cos\theta\pm i\sin\theta)$

고유값으로 사용합니다.따라서 cos ${\displaystyle 1}$ ±$$1 { $displaystyle \cos \theta \neq$ \pm 1$$}에는 항상 실제 고유값이 없습니다.즉, 평면 내의 실제 벡터는 A에 의해 변경되지 않습니다.

3차원의 회전각과 축

트레이스가 불변임을 알면 적절한 직교 3x3 $회전행렬{\displaystyle }$ A$(\displaystyle$ A$)$의 $(\$$displaystyle$$\alpha)$는 다음과 같이 구할 수 있습니다.

$({displaystyle \alpha =\cos ^{-1}\leftfrac {A_{11}+A_{22}+A_{33)-1}{2}\right})$

이 공식은 주 아크 코사인에서 0${\displaystyle \le }$α , 180 ${\displaystyle {\mathrm{the}}^{}}$ { $displaystyle$ 0$\leq \leq 180^{\circ$을 만족하는 회전각을 구한다.회전 각도를 180도를 초과하지 않도록 제한하는 방향을 가리키도록 해당 회전 축을 정의해야 합니다.($축{\displaystyle }$m을 중심으로 180도 이상의 회전(\$displaystyle$ m$)$을 n $=$ -$m$으로 대체하면 항상 0${\displaystyle {\mathrm{\alpha \alpha }}^{}}$) 180${\$ {\$displaystyle 0\leq$ \$leq 180^{\$$displaystyle n=-$m$}}}$의 회전으로 쓸 수 있기 때문에 항상 가능합니다.)$$

3D 공간의 모든 적절한 $회전{\displaystyle }$ A$(디스플레이 스타일$ A$)$에는 회전 축이 있으며, 회전 축에 정렬된 $벡터{\displaystyle }$ v$(디스플레이 스타일$ v$)$는 회전의 영향을 받지 않도록 정의됩니다.따라서 A ${\displaystyle v}$ ${\displaystyle =}$ {\$displaystyle$ Av$=v$ 및 $회전축$은 고유값 1과 관련된 회전행렬의 고유벡터에 대응한다.$(\displaystyle \alpha)$가 0이 아닌 한(즉, 회전은 항등 텐서가 아님) 그러한 방향은 하나뿐입니다.A에는 실제 성분만 있으므로 최소 하나의 실제 고유값이 있고 나머지 두 고유값은 서로 복잡한 공역이어야 합니다(고유값 및 고유 벡터#고유값 및 특성 다항식 참조).1이 고유값임을 알고 있으면 나머지 두 고유값은 서로에 대한 복소 공역이지만, 이는 두 고유값이 복잡하다는 것을 의미하지는 않습니다. 두 고유값이 이중 다수로 실재할 수 있기 때문입니다.$회전각\alpha {\displaystyle }$ $=$ ${\displaystyle {180}^{}}$µ의 축퇴의 $경우(\displaystyle$ \$alpha$ = $180^{\$display$\}\}),$ 나머지 2개의 고유치는 모두 -1이다.회전각이 0인 축퇴의 경우 회전행렬은 항등이며, 3개의 고유치는 모두 1이다(회전축이 임의인 유일한 경우).

회전축을 찾기 위해 스펙트럼 분석이 필요하지 않다.$(\displaystyle$ n$)$이 회전축에 정렬된 단위 고유 벡터를 나타내고$$α(\$displaystyle \alpha)$가 회전각을 나타내면 ${\displaystyle 2}$ sin${\displaystyle }$δ (${\displaystyle \alpha )}$ n ${\displaystyle =}$ { ${\displaystyle {\mathrm{A}}_{}}$ 32${\displaystyle {}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle {23}_{}}$、${\displaystyle {}_{}{\mathrm{A}}_{}}$ ${\displaystyle {}_{}}$ - A ${\displaystyle {31}_{}{}_{}{}_{}}$ {$displaystyle$2 \ $sin (\alpha ） =$ 로 나타낼 수 $있습니다$.{$A_{32}-A_{23}, A_{13}-A_{311$}, $A_{214-A_{12$ 따라서 이 벡터의 크기가 0이 아닌 경우에는 단순히 정규화함으로써 고유값 분석 비용을 피할 수 있다$.$한편, 이 벡터가 0이면 sin${\displaystyle \theta }$ ${\displaystyle (}$α) $=$ ${\displaystyle 0}$(\$displaystyle$\sin(\alpha)=$0$이 된다. 즉, 이 벡터는 회전 각도가 0도 또는 180도인 경우에만 0이 되며, 이 경우 A${\displaystyle }$+ ${\displaystyle I}$(\$display$ A$+I)$의 열을 정규화함으로써 회전 축을 할당할 수 있다.진도 ^[2]0이 아닙니다.

이 설명은 적절한 회전에 적용되므로 ${\displaystyle \det }$ A ${\displaystyle =}$ $(\displaystyle \det$ A$=1$입니다. 부적절한 직교 3x3 $매트릭스{\displaystyle }$B(\$displaystyle$ B$)$는 B $=$- ${\displaystyle A}$(\$displaystyle$ B$=-A$로 표시될 수 있습니다. $여기$서 A(\$displaystyle A)$는 적절한 직교입니다.즉, 부적절한 직교 3x3 행렬은 적절한 회전(위에서 설명한 바와 같이 회전 축을 찾을 수 있음)에 이어 반전(-1의 곱셈)으로 분해될 수 있습니다.따라서$A의$$$회전축은 $-1$의 고유값에 대응하는$B의$고유벡터이기도 합니다.

회전면

모든 3차원 회전에는 회전축이 있듯이, 모든 3차원 회전에는 회전축에 수직인 평면이 있으며 회전축에 의해 변하지 않습니다.이 평면으로 제한된 회전은 일반적인 2D 회전입니다.

증명은 위의 논의와 유사하게 진행됩니다.먼저 3D 회전 행렬 A의 모든 고유값이 실재한다고 가정합니다.즉, 해당 고유 벡터(필연적으로 직교)에 의해 만들어지는 직교 기저가 있으며, 그 위에 회전 행렬의 효과가 직교 기저를 늘립니다.이 기준에서 A를 쓰면 대각선이지만 대각선 직교 행렬은 대각선 입력에 +1과 -1로만 구성됩니다.그러므로, 우리는 제대로 된 회전을 가지고 있지 않지만, 일련의 성찰의 결과나 동일성을 가지고 있다.

따라서 적절한 회전은 몇 가지 복잡한 고유값을 가집니다.v를 대응하는 고유 벡터라고 하자.$이전{\displaystyle \stackrel{}{}}$ 항목에서 설명한 것처럼 v ${\(\$도 고유 벡터이며 $v{\displaystyle }$+ ${\displaystyle v\stackrel{}{}}${\(\$displaystyle$ v$+{\bar {v}})$ $및$ i${\displaystyle (v}$- $))$ {$displaystyle$ i$(v-{\bar {v}})$도 스칼라 곱이 사라집니다.

$\displaystyle i(v^){T}+{\bar {v}^{T}(v-{\bar {v}})=i(v^{T}v-{\bar {v}}^{T}{\bar {v}}+{\bar {v}}^{T}v-v^{T}{\bar {v}})=0}$

왜냐하면 v t${\displaystyle {\stackrel{}{}t}^{}}$ ${\displaystyle {}^{}\stackrel{}{}}$ {\$display{\displaystyle {\stackrel{}{}}^{}}$ display display display display v v 、 { $display$style { $v$$}^{$$T}{\bar {v}}$은(는) 실재합니다.복잡한 $켤레{\displaystyle {}^{}}$ ${\displaystyle v^{}}$ T$$ {\$displaystyle$$$v$^{T$$v{\displaystyle {\stackrel{}{}}^{}}$ 및 v$t$ T$$v ${\displaystyle$ {$v}^{$$T}v$$}$ 및 ${\displaystyle V^{}}$ ${\displaystyle {}^{}\stackrel{}{}}$ ${\$ { \ $display style$ v$$$}$ { \$bar$ { $v$}$$are$$ 、$$v { \ $display style$ v$$ }와 v ${\$ { \ $display$ style { $v$} 사이의 $동일$한 스칼라 곱을 나타냅니다.

$즉{\displaystyle ,}$ v + ${\displaystyle v\stackrel{}{}}$ ${\$ { $display$ v + { \$bar$ { $v$} $i$ (${\displaystyle }$i (${\displaystyle v}$ - ${\displaystyle v\stackrel{}{}}$ ${\displaystyle ¯}$) { $display style$i ( v - { \$bar$ { $v$} )는$$ 직교 벡터입니다.또한, 둘 다 구조상 실재 벡터이다.이러한 벡터는$$v\$displaystyle$$$v$$ 및 $v$${\\$와 $동일$한 부분 공간에 걸쳐 있습니다.이것은 A의 적용에 따른 불변 부분 공간입니다.따라서 이들은 불변 평면에 걸쳐 있습니다.

이 평면은 A의 고유 벡터의 직교성 때문에 고유 값이 1인 A의 나머지 고유 벡터에 해당하는 불변 축과 직교합니다.

「 」를 참조해 주세요.

레퍼런스

외부 링크

• "Rotation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• cut-the-knot.org 로테이션 제품 (Cut-the-Rotations at Cut-the-Rotations cut-the-knot.org
• 삼각형이 Equilateral인 경우. cut-the-knot.org
• 극좌표를 사용한 점 회전, howtoproperly.com
• Roger Germundsson의 작업 후 Sergio Hannibal Mejia의 2차원 회전과 Roger Germundsson의 3D 회전 이해, 울프램 시연 프로젝트.데모를 실시합니다.wolfram.com
• 회전, 반사 및 프레임 변경: IOP 퍼블리싱 컴퓨터 엔지니어링 역학의 직교 텐서