원대칭
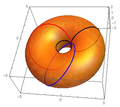
Circular symmetry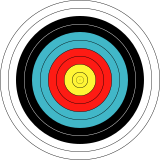 2차원에서 활쏘기 표적은 원형 대칭을 가지고 있다. |  회전면은 축을 중심으로 한 원형의 대칭을 3차원으로 가진다. |
기하학에서, 원형 대칭은 임의의 각도로 회전하고 그 위에 매핑할 수 있는 평면 물체에 대한 연속 대칭의 한 종류입니다.
회전원대칭은 복소평면 내의 원군 또는 특수직교군 SO(2) 및 유니터리군 U(1)와 동형이다.반사원대칭은 직교군 O(2)와 동형이다.
두 치수
원형 대칭을 가진 2차원 개체의 동심원과 환상 영역의 거리로 구성되었다.
회전 원형 대칭 하위 집단 대칭으로 모든 순환 대칭이 아연을 가지고 있다.반사하는 성질을 띈 원형 대칭 하위 집단 대칭으로 모든 이면체 대칭, Dihn다.
3치수
3-dimensions에서, 혁명의 표면이나 고첸 축을 중심으로 원형 대칭, 또한 원통형 대칭 또는 축대칭을 갖추고 있다.예는 올바른 원뿔.3차원으로 원형으로 된 대칭 여러 종파로 모든 피라미드의 대칭 Cnv다.
Adouble-cone, 두 원뿔을 합친 모양, 실린더, 환상 면과 회전 타원체다 원형 대칭과 외에 좌우 대칭 시스템(또는 반은 원통형 대칭)의 축에perpendular다.이 반사 원형 대칭 여러 종파로 모든 이산 프리즘 대칭 Dnh다.
4차원
 (표준) |  1:5 |  5:1 |
| 원통형 | 듀오실린드리컬 | |
|---|---|---|
4차원에서 물체는 두 개의 직교 축 평면에서 원형 대칭을 가질 수도 있고 이중 원통 대칭을 가질 수도 있습니다.예를 들어 듀오실린더와 클리포드 토러스는 2개의 직교축에서 원형 대칭을 가진다.1개의 3공간에서 구대칭, 직교방향에서 원대칭으로 이루어진 스피린더.
구면 대칭

유사한 3차원 등가항은 구면대칭이다.
회전구대칭은 회전군 SO(3)와 동일하며 데이븐포트 연쇄회전 피치, 요 및 롤에 의해 파라미터화할 수 있다.회전 구면 대칭에는 모든 이산 카이랄 3D 점 그룹이 부분군으로 포함됩니다.반사구대칭은 직교군 O(3)와 동형상이며, 3차원 이산점군을 서브그룹으로 한다.
스칼라 장은 중심력의 전위와 같이 원점까지의 거리에만 의존할 경우 구면 대칭을 갖는다.벡터장은 중심력과 같은 원점까지의 거리에만 따라 크기 및 방향(내향/외향)[citation needed]을 갖는 반경방향 내향 또는 외향일 경우 구면대칭성을 가진다.



