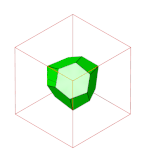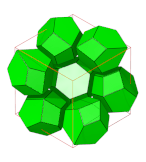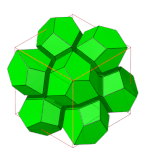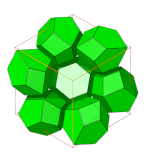
벌집(지오메트리)

기하학에서 벌집이란 다면체나 고차원 세포의 촘촘한 패킹이나 공간을 채워서 틈이 생기지 않도록 하는 것이다. 그것은 어떤 차원에서도 보다 일반적인 수학적 타일링 또는 테셀레이션의 예다. 그것의 치수는 n차원 공간의 벌집을 위한 n-허니콤으로 명확히 할 수 있다.

허니컴은 보통 유클리드("평평한") 공간에 건설된다. 그것들은 쌍곡선 벌집과 같은 비유클리드 공간에서 만들어질 수도 있다. 어떤 유한 균일 폴리토프는 구면 공간에 균일한 벌집을 형성하기 위해 그것의 원주에 투영될 수 있다.

예를 들어 벽돌 벽 패턴에서처럼 직사각형을 사용하여 모서리에서 만나지 않는 다각형으로 평면을 채우는 것이 가능하다: 이것은 모서리가 인접한 다각형의 가장자리를 따라 부분적으로 놓여 있기 때문에 적절한 타일링이 아니다. 마찬가지로, 적절한 벌집형에서는 인접한 셀의 얼굴을 따라 부분적으로 놓여 있는 가장자리나 정점이 없어야 한다. 각 벽돌면을 두 개의 내부 각도가 180도인 육각으로 해석하면 패턴을 적절한 타일링으로 간주할 수 있다. 그러나 모든 기하학자들이 그런 육각형을 받아들이는 것은 아니다.

분류

일부분만 분류된 허니컴이 무한히 많다. 더 많은 규칙적인 것들이 가장 많은 관심을 끌었고, 반면에 풍부하고 다양한 종류의 다른 것들이 계속해서 발견되고 있다.

가장 간단하게 만들 수 있는 벌집들은 비행기의 일부 테셀레이션을 바탕으로 겹겹이 쌓이거나 프리즘의 슬래브로부터 형성된다. 특히 평행한 모든 공간에 대해 복사가 공간을 채울 수 있는데, 큐빅 벌집합은 일반(유클리드) 공간에서 유일한 정기 벌집이기 때문에 특별하다. 또 다른 흥미로운 가족은 힐 사트라헤드라와 그들의 일반화인데, 이것은 공간을 타일로 만들 수도 있다.

유니폼 3-허니콤

3차원 균일 벌집이란 균일한 다면세포로 구성된 3-공간 내의 벌집형이며, 모든 정점을 가지고 있다(즉, [타일링을 보존하는 3-공간의 등각형]의 그룹은 정점에 전이된다). 유클리드 3공간에 28개의 볼록한 예가 있는데,^[1] 아르키메데스 꿀콤이라고도 한다.

꿀벌집합은 타일링을 보존하는 이소메트리 집단이 깃발에 전이적으로 작용하면 규칙적인 것으로 불리는데, 여기서 깃발은 세포 위에 누운 얼굴 가장자리에 놓여 있는 꼭지점이다. 보통의 벌집마다 자동으로 균일하다. 그러나 유클리드 3공간인 입방형 벌집에는 단 한 개의 규칙적인 벌집이 있다. 2는 준정형(일반 세포의 두 종류로 만들어짐)이다.

유형	정규 큐빅 벌집	퀘이레겔러 꿀콤
세포	큐빅	팔면체 및 사면체
슬래브 레이어

사면체-옥타면체 벌집과 계정체 사면체-옥타면체 벌집들은 각각 사면체와 옥타면체를 번갈아 가며 세포의 슬래브 층 3 또는 2 위치에 의해 생성된다. 이러한 슬래브 층을 반복하는 패턴의 높은 순서에 의해 무한히 많은 독특한 벌집들이 만들어질 수 있다.

공간을 채우는 다면체

대칭 내에서 모든 세포를 동일시하는 벌집합은 세포 전이성 또는 이소염색체라고 한다. 3차원 유클리드 공간에서는 이런 벌집형 세포가 공간을 채우는 다면체라고 한다.^[2] 다면체가 공간을 채우는 다면체가 되기 위해 필요한 조건은 그 다면체의 딘 불변성이 입방체 이외의 플라토닉 고형물을 배제한 0이어야 한다는 것이다.^[3]^[4]

5개의 공간을 채우는 폴리헤드라는 번역만으로 3차원 유클리드 공간을 테셀레이션할 수 있다. 그들은 paralleloedra라고 불린다.

큐브 (병렬)	육각 프리즘	롬빅 도데카헤드론	길쭉한 도데카헤드론	잘린 팔면체
입방 벌집	육각 프리즘 벌집	롬빅도데카헤드라속	길쭉한 도데카헤드라	잘린 옥타헤드라

3 가장자리-모서리-모양	3+1 가장자리-모서리-모서리	4 가장자리-모양	4+1 가장자리-모서리-모서리	6 가장자리-모서리-모양

공간을 채우는 다면체의 다른 알려진 예는 다음과 같다.

삼각 프리즘 벌집
회전 삼각 프리즘 벌집
3각형 벌집이 잘려나간 4각형 벌집이다. 다이아몬드에 있는 탄소 원자의 보로노이 세포는 이 모양이다.^[8]
트라페조-롬브 도데카헤드랄 벌집^[9]
등면 기울기^[10]

2개 이상의 다면체가 있는 기타 허니컴

때로는 둘 이상의 다른 다면체를 결합하여 공간을 채울 수도 있다. 많은 균일한 꿀벌들 외에도, 잘 알려진 또 다른 예는 웨이어-이다.패트레이트 하이드레이트 결정 구조에서 채택된 펠란 구조

웨이어의 주기적인 단위펠란 구조.

P8 tiling (with left and right-handed cells)

동일한 다면체의 왼손 및 오른손 버전에 의한 벌집.

논콘벡스 3허니콤

문서화된 예는 드물다. 다음 두 가지 클래스를 구분할 수 있다.

겹치지 않고 포장되는 비콘벡스 세포로, 오목한 다각형의 기울기와 유사하다. 여기에는 요시모토 큐브에서와 같이 작은 나선형 도데카헤드론의 패킹이 포함된다.
양의 밀도와 음의 밀도가 '취소'되어 균일하게 밀집된 연속체를 형성하는 셀의 중첩은 평면의 겹치는 기울기와 유사하다.

쌍곡선 허니컴

3차원 쌍곡선 공간에서 다면체의 이면각은 크기에 따라 달라진다. 따라서 정규 쌍곡선 꿀벌집에는 각 가장자리에서 도데카헤드라 미팅이 4개 또는 5개 있는 2개가 포함된다. 이들의 이면각은 thus/2와 2π/5이며, 이 두 개 모두 유클리드 도데카헤드론보다 작다. 이러한 효과와는 별개로 쌍곡선 허니콤은 유클리드 허니콤이나 폴리초라와 동일한 위상학적 제약조건을 따른다.

4개의 컴팩트하고 11개의 파라콤팩트 일반 쌍곡선 꿀컴과 많은 컴팩트하고 파라콤팩트 균일한 쌍곡선 꿀컴이 열거되었다.

일반³ 소형 허니컴 4개 H
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

11개의 파라콤팩트 일반 꿀벌집
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

3-허니콤의 이중성

모든 벌집에는 이중 벌집합이 있으며, 이는 다음과 같이 교환하여 얻을 수 있다.

정점 세포

가장자리 면

동심원 하이퍼바이저에 대한 통상적인 유한한 상호주의 방법이 문제에 부딪힐 수 있다는 점을 제외하면, 이것들은 단지 4차원 4폴리탑을 이원화하는 규칙일 뿐이다.

일반 허니컴이 깔끔하게 이중화될수록:

큐빅 벌집합은 자가이중이다.
옥타헤드라와 사트라헤드라의 그것과 Rhombic dodecheredra의 그것과 이중이다.
균일한 평면 기울기에서 파생된 슬래브 허니콤은 기울기와 동일한 방식으로 서로 이중적이다.
나머지 아르키메데스 벌집들의 이중은 모두 세포 전이적이며 인치발트에 의해 설명되어 왔다.^[13]

자가이중 벌집

허니컴은 또한 스스로 이중화 될 수 있다. Schléfli 기호 {4,3,4ⁿ⁻²}이(가) 있는 모든 n차원 하이퍼큐브 허니컴은 자체 이중이다.

참고 항목

참조

^ 그룬바움(1994년). "3공간의 균일한 기울기" Gembinatorics 4(2)
^ Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
^ Debrunner, Hans E. (1980), "Über Zerlegungsgleichheit von Pflasterpolyedern mit Würfeln", Archiv der Mathematik (in German), 35 (6): 583–587, doi:10.1007/BF01235384, MR 0604258, S2CID 121301319.
^ Lagarias, J. C.; Moews, D. (1995), "Polytopes that fill $\mathbb {R} ^{n}$ and scissors congruence", Discrete and Computational Geometry, 13 (3–4): 573–583, doi:10.1007/BF02574064, MR 1318797.
^ [1] 삼각, 사각, 육각 프리즘을 이용한 균일한 공간 채우기
^ [2] rhombo-hexangular 도데카헤드라만을 사용한 균일한 공간 채우기
^ [3] 잘린 옥타헤드라만을 사용한 균일한 공간 채우기
^ John Conway (2003-12-22). "Voronoi Polyhedron. geometry.puzzles". Newsgroup: geometry.puzzles. Usenet: Pine.LNX.4.44.0312221226380.25139-100000@fine318a.math.Princeton.EDU.
^ X. 첸, D. 스트라스와 T. 슐릭, J. Compute. 화학. 22(15) 1843–1850(2001)
^ [4] O. 델가도 프리드리히스와 M. 오키프 등면 단순 기울기: 이항 및 <16면>이 있는 타일로 한다. 액타 크리스탈로그르 (2005) A61, 358-362
^ [5] 2015-06-30년 루게로의 웨이백 머신 가브브리엘리에 보관. 치랄 카피로 공간을 채우는 13면 다면체.
^ 폴링, 리너스 화학적 결합의 특성. 코넬 대학교 출판부, 1960년
^ Inchbald, Guy (July 1997), "The Archimedean honeycomb duals", The Mathematical Gazette, 81 (491): 213–219, doi:10.2307/3619198, JSTOR 3619198.

추가 읽기

Coxeter, H. S. M.: 일반 폴리토페스.
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. pp. 164–199. ISBN 0-486-23729-X. 5장: 폴리헤드라 패킹 및 공간충전
크래틀로우, K.: 우주에서 주문하다.
피어스, P.: 자연 속의 구조는 디자인을 위한 전략이다.
Goldberg, Michael 3 무한가족 사면공간-필러 저널의 결합 이론 A, 16, 페이지 348–354, 1974.
Goldberg, Michael (1972). "The space-filling pentahedra". Journal of Combinatorial Theory, Series A. 13 (3): 437–443. doi:10.1016/0097-3165(72)90077-5.
골드버그, 마이클 더 스페이스필링 펜타헤드라 II, 저널 오브 콤비네이터얼 이론 17 (1974), 375–378.
Goldberg, Michael (1977). "On the space-filling hexahedra". Geometriae Dedicata. 6. doi:10.1007/BF00181585. S2CID 189889869.
Goldberg, Michael (1978). "On the space-filling heptahedra". Geometriae Dedicata. 7 (2): 175–184. doi:10.1007/BF00181630. S2CID 120562040.
골드버그, 마이클 볼록스 다면체 공간-12면 이상의 필러. 검. 데디카타 8, 491-500, 1979.
Goldberg, Michael (1981). "On the space-filling octahedra". Geometriae Dedicata. 10 (1–4): 323–335. doi:10.1007/BF01447431. S2CID 189876836.
Goldberg, Michael (1982). "On the Space-filling Decahedra". {{cite journal}}: Cite 저널은 필요로 한다. journal= (도움말)
Goldberg, Michael (1982). "On the space-filling enneahedra". Geometriae Dedicata. 12 (3). doi:10.1007/BF00147314. S2CID 120914105.

외부 링크

Olshevsky, George. "Honeycomb". Glossary for Hyperspace. Archived from the original on 4 February 2007.
5개의 공간을 채우는 다면체, Guy Inchbald, The Mathemical Gazette 80, 1996년 11월 페이지 466-475.
T.E.의 Raumfueller (공간에 다면체를 채우는 것) 도로진스키
Weisstein, Eric W. "Space-Filling Polyhedron". MathWorld.

v t 치수 2-9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\tilde{A}_{n-1$	${\tilde{C}_{n-1$	${\tilde{B}_{n-1$	${\tilde{D}_{n-1$	${\tilde {G}}_{2}$ ~ ${\tilde {G}}_{2}$ ${\$ G} ${\tilde {G}}_{2}$ ${\tilde {F}}_{4}$ 2}} ${\tilde {F}}_{4}$ / F ~ 4 {\ $displaystyle {\tilde{F}_{4}}$ ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$ ~ ${\tilde {E}}_{n-1}$ ${\$ }
E²	균일 타일링	{3^[3]}	δ₃	Δ₃	Δ₃	육각형
E³	균일볼록 벌집	{3^[4]}	δ₄	Δ₄	Δ₄
E⁴	제복4벌집	{3^[5]}	δ₅	Δ₅	Δ₅	24셀 벌집
E⁵	제복5벌집	{3^[6]}	δ₆	Δ₆	Δ₆
E⁶	제복6벌집	{3^[7]}	δ₇	Δ₇	Δ₇	2₂₂
E⁷	제복7허니콤	{3^[8]}	δ₈	Δ₈	Δ₈	1₃₃ • 3₃₁
E⁸	제복8벌집	{3^[9]}	δ₉	Δ₉	Δ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	제복9벌집	{3^[10]}	δ₁₀	Δ₁₀	Δ₁₀
E¹⁰	제복10벌집	{3^[11]}	δ₁₁	Δ₁₁	Δ₁₁
E^n-1	제복(n-1)-벌집합	{3^[n]}	δ_n	Δ_n	Δ_n	1_k2 • 2_k1 • k₂₁

[1] 그룬바움(1994년). "3공간의 균일한 기울기" Gembinatorics 4(2)

[2] Weisstein, Eric W. "Space-filling polyhedron". MathWorld.

[3] Debrunner, Hans E. (1980), "Über Zerlegungsgleichheit von Pflasterpolyedern mit Würfeln", Archiv der Mathematik (in German), 35 (6): 583–587, doi:10.1007/BF01235384, MR 0604258, S2CID 121301319.

[4] Lagarias, J. C.; Moews, D. (1995), "Polytopes that fill $\mathbb {R} ^{n}$ and scissors congruence", Discrete and Computational Geometry, 13 (3–4): 573–583, doi:10.1007/BF02574064, MR 1318797.

[5] [1] 삼각, 사각, 육각 프리즘을 이용한 균일한 공간 채우기

[6] [2] rhombo-hexangular 도데카헤드라만을 사용한 균일한 공간 채우기

[7] [3] 잘린 옥타헤드라만을 사용한 균일한 공간 채우기

[8] John Conway (2003-12-22). "Voronoi Polyhedron. geometry.puzzles". Newsgroup: geometry.puzzles. Usenet: Pine.LNX.4.44.0312221226380.25139-100000@fine318a.math.Princeton.EDU.

[9] X. 첸, D. 스트라스와 T. 슐릭, J. Compute. 화학. 22(15) 1843–1850(2001)

[10] [4] O. 델가도 프리드리히스와 M. 오키프 등면 단순 기울기: 이항 및 <16면>이 있는 타일로 한다. 액타 크리스탈로그르 (2005) A61, 358-362

[11] [5] 2015-06-30년 루게로의 웨이백 머신 가브브리엘리에 보관. 치랄 카피로 공간을 채우는 13면 다면체.

[12] 폴링, 리너스 화학적 결합의 특성. 코넬 대학교 출판부, 1960년

[13] Inchbald, Guy (July 1997), "The Archimedean honeycomb duals", The Mathematical Gazette, 81 (491): 213–219, doi:10.2307/3619198, JSTOR 3619198.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[13]

Search