계측 변수 추정

통계, 계량경제학, 역학 및 관련 분야에서는 통제된 실험이 불가능하거나 ^[1]무작위 실험에서 치료가 모든 단위에 성공적으로 전달되지 않을 때 인과 관계를 추정하기 위해 계측 변수 방법(IV)을 사용한다.직관적으로 IV는 관심 있는 설명 변수가 오차항과 상관되어 있을 때 사용되며, 이 경우 일반 최소 제곱과 분산 분석은 치우친 결과를 제공합니다.유효한 수단은 설명 변수의 변화를 유도하지만 종속 변수에 대한 독립적 영향은 없으므로 연구자가 종속 변수에 대한 설명 변수의 인과적 영향을 밝혀낼 수 있다.

계측 변수 방법을 사용하면 설명 변수(공변수)가 회귀 모형의 오차 항과 상관되어 있을 때 일관된 추정을 할 수 있습니다.이러한 상관관계는 다음과 같은 경우에 발생할 수 있습니다.

종속 변수의 변경은 공변량 중 하나 이상의 값을 변경합니다("변형" 원인).
종속 변수와 독립 변수 모두에 영향을 미치는 생략된 변수가 있습니다.
공변량은 비균형 측정 오차의 영향을 받습니다.

회귀의 맥락에서 이러한 문제 중 하나 이상을 겪는 설명 변수를 내생적 변수라고 부르기도 합니다.이 경우 일반 최소 제곱은 치우쳐 있고 일관되지 않은 ^[2]추정치를 생성합니다.그러나 금융상품을 이용할 수 있는 경우에도 일관된 추정치를 얻을 수 있다.계측기는 그 자체는 설명 방정식에 속하지 않지만 조건부로 다른 공변량의 값에 따라 내생적 설명 변수와 상관되는 변수입니다.

선형 모델에서는 IV를 사용하기 위한 두 가지 주요 요건이 있습니다.

계측기는 조건부로 다른 공변량을 기준으로 내생적 설명 변수와 상관되어야 합니다.이 상관관계가 강하면 계측기의 첫 번째 단계가 강하다고 합니다.상관 관계가 약하면 모수 추정치와 표준 ^[3]^[4]오차에 대해 잘못된 추론을 제공할 수 있습니다.
계측기는 조건부로 다른 공변량에 대해 설명 방정식의 오차항과 상관할 수 없습니다.즉, 기기가 원래 예측 변수와 동일한 문제를 겪을 수 없습니다.이 조건이 충족되면 계측기는 제외 제한을 충족하는 것으로 간주됩니다.

역사

악기 변수를 처음 사용한 것은 1928년 필립 G의 책이다.1900년대 초 미국에서 ^[5]^[6]식물성 기름과 동물성 기름의 생산, 운송 및 판매에 대한 뛰어난 설명으로 가장 잘 알려진 라이트는 1945년 Olav Reiersöl이 논문에서 가변 오차 모델의 맥락에서 동일한 접근방식을 적용하여 이 방법을 ^[7]명명했습니다.

Wright는 미국에서 판매되는 가격과 수량에 대한 패널 데이터를 사용하여 버터의 공급과 수요를 파악하려고 했습니다.이는 수요 또는 공급 곡선이 가격과 수요 또는 공급 수량 사이의 경로에 의해 형성되기 때문에 회귀 분석이 수요 또는 공급 곡선을 생성할 수 있다는 것이었다.문제는 관측 데이터가 수요나 공급 곡선을 형성하지 않고 다양한 시장 조건에서 다른 형태를 취하는 점 관측의 구름을 형성한다는 것이었다.데이터로부터 추론하는 것은 여전히 어려운 것 같았다.

문제는 가격이 공급과 수요 모두에 영향을 미쳐 관측 데이터에서 직접 둘 중 하나만 설명하는 함수를 구성할 수 없다는 것이었다.Wright는 수요와 공급 중 어느 쪽이든 상관관계가 있는 변수, 즉 도구적 변수가 필요하다고 올바르게 결론지었다.

심사숙고 끝에, 라이트는 지역별 강우를 그의 도구 변수로 사용하기로 결정했다: 그는 강우가 잔디 생산과 우유 생산에 영향을 미치고 궁극적으로 버터 공급에 영향을 미치지만 버터 수요에는 영향을 미치지 않는다고 결론지었다.이러한 방법으로 그는 가격과 ^[8]공급이라는 수단 변수만으로 회귀 방정식을 구성할 수 있었다.

이론.

IV 뒤에 있는 아이디어는 광범위한 모델의 클래스로 확장되지만, IV에 대한 매우 일반적인 맥락은 선형 회귀입니다.전통적으로 ^[9]계측 변수는 선형 방정식의 "오류항" U와 상관되지 않고 독립 변수 X와 상관된 변수 Z로 정의됩니다.

Y=X\beta +U

$Y는$ 벡터입니다 $.$ $(\displaystyle$ X $)$ 는 $X$ 일반적으로 1개의 열이 있는 행렬이며, 다른 공변량에는 추가 열이 있을 수 있습니다.계측기에서 $\beta$ β(\ $displaystyle\beta)$ 를 $\beta$ 복구할 수 있는 $\beta$ 을 고려하십시오. ${\widehat {\beta }}$ 는 $\operatorname {cov} (X,{\widehat {U}})=0$ ${\widehat {\beta }}$ $\operatorname {cov} (X,{\widehat {U}})=0$ {\ $displaystyle$ ${\widehat {\beta }}$ {\ $widehat$ $\operatorname {cov} (X,{\widehat {U}})=0$ } $=$ $(X,$ {\ $widehat {U}})$ = $0($ 오차의 $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ 을 최소화할 때 $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ β( $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ - $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ β) $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ $\operatorname {cov} (X,{\widehat {U}})=0$ ( $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ - X β) β $)$ β(X $\operatorname {cov} (X,{\widehat {U}})=0$ $U$ ^) ^) $\min _{\beta }(Y-X\beta )'(Y-X\beta )$ 0(X)로 ${\widehat {\beta }}$ 해결한다는 점에 유의하십시오.dition은 $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ ( $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ Y - $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ ) $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ ^ $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ { \ $display style$ X （ Y - X { \ display hat } = $X'(Y-X{\widehat {\beta }})=X'{\widehat {U}}=0$ X ' { \ $wide$ hat { U } } = $0$ ）。예를 들어 X $\displaystyle$ X $}$ 와 $X$ Y $\displaystyle$ Y 모두에 $Y$ $X$ 을 주는 생략 변수가 있는 경우 등, 실제 $\operatorname {cov} (X,U)\neq 0$ 의 cov $\operatorname {cov} (X,U)\neq 0$ ( $\operatorname {cov} (X,U)\neq 0$ , U ) $\operatorname {cov} (X,U)\neq 0$ 0 $\operatorname {cov} (X,U)\neq 0$ { $displaystyle \operatorname$ { $cov$ } ( $X$ , $U$ ) \ $neq$ 0 $\operatorname {cov} (X,U)\neq 0$ }이 $\operatorname {cov} (X,U)\neq 0$ (가) 있다고 생각되는 경우, 이 순서는 발생하지 않습니다. $Y$ $(\displaystyle$ Y $Y$ 의 $Y$ (\ $displaystyle$ X $).$ OLS는 단순히 결과오류를 X(\ $displaystyle$ X $X$ 와 무관하게 보이게 하는 파라미터를 선택합니다.

단순화를 위해 단일 변수 대소문자를 고려합니다.하나의 변수와 상수에 대한 회귀 분석을 고려한다고 가정합니다(다른 공변량이 필요하지 않거나 다른 관련 공변량을 부분적으로 제외했을 수 있음).

y=\alpha +\display x+u

이 경우, 관심 회귀체의 계수는 ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ β ^ = ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ , ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ ) var $δ$ ( ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ x ${\widehat {\beta }}={\frac {\operatorname {cov} (x,y)}{\operatorname {var} (x)}}$ ) { displaystyle ${ widehat$ } $= scfrac$ { $operatorname {cov}(x , y$ ) {\ $operatorname {var$ } ( $x$ , y ) $。$ ystyle을 $y$ $y$ 하면 됩니다.

{\displaystyle{\begin{정렬}{\widehat{\beta}}&={\frac{\operatorname{cov}(x, y)}{\operatorname{}())}}={\frac{\operatorname{cov}(x,\alpha +\beta x+u)}{\operatorname{}())}}\\[6pt]&, ={\frac{\operatorname{cov}(x,\alpha +\beta))}{\operatorname{}())}}+{\frac{\operatorname{cov}(x,u)}{\operatorname{}())}}=\beta ^{.*}와{\frac {\operatorname {cov}(x,u)}{\operatorname {var}(x)}},\end {aligned}}

$\beta ^{*}$ 서 β β $∗$ { $displaystyle$ \ $displaystyle ^{*}}$ 는 $\beta ^{*}$ x가 u와 상관관계가 없는 경우 추정 계수 벡터가 되는 값이다.이 경우, β $\beta ^{*}$ δ {\ $displaystyle \beta ^{*}}$ 는 $\beta ^{*}$ $\beta .$ β $\beta .$ . {\ $displaystyle \beta$ }의 $\beta .$ 편향되지 않은 $\beta ^{*}$ 을 알 수 있다. 만약 $\operatorname {cov} (x,u)\neq 0$ δ ( $\operatorname {cov} (x,u)\neq 0$ , $\operatorname {cov} (x,u)\neq 0$ ) ${\$ $\operatorname {cov} (x,u)\neq 0$ { $displaystyle \operatorname$ { $cov （ x$ , $u$ )\ $neq$ 0 }이면 $\operatorname {cov} (x,u)\neq 0$ OLS는 계수를 반영하지 않는다.erest. IV는x가u\ $displaystyle$ u와 $x$ $u$ 한지 $아닌$ 다른 $변수$ z $\displaystyle$ z가 $z$ u $\displaystyle$ 와 무관한지 여부에 따라 ${\beta }$ $β$ 를 ${\beta }$ 식별함으로써 이 문제를 해결하는 데 도움이 됩니다.이론에 따르면 $z$ 는 u $displaystyle$ u와 무관합니다. $\$ $displaystyle$ z는 x $($ 첫 $z$ 번째 단계)와 관련이 있지만u $($ 제한)와는 관련이 없습니다.그러면 IV는 OLS가 실패하는 원인 파라미터를 식별할 수 있습니다.선형적인 경우(IV, 2SLS, GMM)에서도 IV 추정기를 사용하고 도출하는 방법은 여러 가지가 있기 때문에 아래의 추정 섹션에 대한 자세한 설명은 생략합니다.

예

비공식적으로, 어떤 변수 X가 다른 Y에 미치는 인과적 영향을 추정할 때, 계측기는 X에 대한 영향을 통해서만 Y에 영향을 미치는 세 번째 변수 Z이다.예를 들어, 한 연구자가 흡연이 일반 ^[10]건강에 미치는 인과적 영향을 추정하려고 한다고 가정합니다.건강과 흡연의 상관관계는 우울증과 같은 다른 변수들이 건강과 흡연 모두에 영향을 미칠 수 있기 때문에, 또는 건강이 흡연에 영향을 미칠 수 있기 때문에 흡연이 나쁜 건강을 야기한다는 것을 의미하지는 않습니다.일반 인구의 흡연 상태에 대한 통제된 실험을 하는 것은 기껏해야 어렵고 비용이 많이 든다.연구자는 담배 제품의 세율을 흡연 수단으로 사용하여 관찰 데이터를 통해 흡연이 건강에 미치는 인과적 영향을 추정할 수 있다.담배 제품에 대한 세율은 흡연에 대한 영향을 통해서만 건강과 상관할 수 있다고 생각하기 때문에 기구에 대한 합리적인 선택이다.만약 연구자가 담배세와 건강 상태가 상관관계가 있다는 것을 발견한다면, 이것은 흡연이 건강에 변화를 일으킨다는 증거로 볼 수 있다.

Angrist와 Krueger(2001)는 도구 변수 ^[11]기법의 역사와 사용에 대한 조사를 제공한다.

그래픽 정의

물론 IV 기법은 훨씬 더 광범위한 비선형 모델들 사이에서 개발되었다.Pearl(2000; 페이지 248)^[12]은 반사실적 형식주의와 그래픽 형식주의를 사용하여 도구 변수에 대한 일반적인 정의를 제시하였다.그래픽 정의를 사용하려면 Z가 다음 조건을 충족해야 합니다.

\displaystyle(Z\perp\!!)\!\perp Y)_{G_{\overline {X}}\qquad(Z\not \!!\!)(웃음) (***************)\!\perp }X)_{G}

여기서 $\perp \!\!\!\perp$ wheredisplay displaydisplay $\perp \!\!\!\perp$ （ \ $displaystyle$ \ $perp$ \ $\perp \!\!\!\perp$ ! ）。 $\!\perp }$ 는 $\perp\!\!\!\perp$ d-separation, $G_{\overline {X}}$ X ${\$ {\ $displaystyle G_{\overline {X}}$ 는 $G_{\overline{X}}$ X로 들어가는 모든 화살표가 끊긴 그래프를 나타냅니다.

반사실적 정의를 위해서는 Z가 다음을 충족해야 한다.

\displaystyle(Z\perp\!!)\!\perp Y_{x}\qquad(Z\not \!!\!)(웃음) (***************)\!\perp }X)}

여기서_x Y는 X와 $⊥(\displaystyle \perp \!!)$ 일 경우 Y가 얻을 수 있는 값을 나타냅니다. $\!\perp }$ 는 $\perp\!\!\!\perp$ 독립성을 나타냅니다.

추가 공변량 W가 있는 경우, 주어진 기준이 W를 조건으로 유지되면 Z가 계측기로 적합하도록 위의 정의가 수정됩니다.

Pearl의 정의의 본질은 다음과 같습니다.

관심의 방정식은 "구조적"이지 "회귀적"이 아닙니다.
오차항 U는 X가 일정하게 유지될 때 Y에 영향을 미치는 모든 외인자를 나타냅니다.
기기 Z는 U와 독립적이어야 합니다.
X가 일정하게 유지되면 기기 Z가 Y에 영향을 미치지 않아야 합니다(제외 제한).
기기 Z가 X와 독립되어 있으면 안 됩니다.

이러한 조건은 방정식의 특정 함수 형식에 의존하지 않으므로 U가 비첨가적일 수 있는 비선형 방정식에 적용할 수 있습니다(비모수 분석 참조).X(및 기타 요인)가 여러 중간 변수를 통해 Y에 영향을 미치는 다중 방정식 시스템에도 적용할 수 있습니다.계측 변수가 X의 원인이 될 필요는 없으며, 조건 1~5를 ^[12]충족하는 경우 그러한 원인의 대리인을 사용할 수도 있다.제외 제한(조건 4)은 중복되며, 이는 조건 2와 3에 따른다.

적합한 기기 선택

U는 관측되지 않기 때문에, Z가 U로부터 독립적이라는 요건은 데이터에서 추론할 수 없으며 대신 모델 구조, 즉 데이터 생성 프로세스에서 결정되어야 한다.인과관계 그래프는 이 구조의 표현이며, 위에 제시된 그래픽 정의를 사용하여 변수 Z가 공변량 W의 집합에 주어진 도구 변수로 적합한지 여부를 신속하게 결정할 수 있다.방법을 확인하려면 다음 예를 참조하십시오.

그림 1: 라이브러리 시간에 따라 근접성이 중요한 변수로 지정됨
그림 2: $G_{\overline {X}}$ $G_{\overline {X}}$ ${\$ {\ $displaystyle G_{\overline {X$ 근접이 인스트루멘털 변수인지 여부를 판단하기 위해 사용한다.
그림 3: 라이브러리 시간이 지정된 경우 근접성이 중요한 변수로 인정되지 않음
그림 4: 근접성은 라이브러리 시간을 공변량으로 포함하지 않는 한 도구 변수로 간주됩니다.

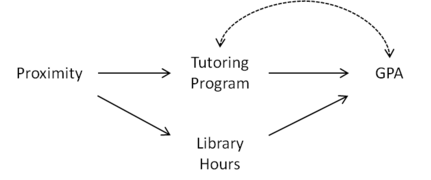
대학 과외 프로그램이 성적 평균(GPA)에 미치는 영향을 추정하려고 합니다.과외 프로그램에 참여하는 것과 GPA 간의 관계는 여러 요인에 의해 혼동될 수 있습니다.과외 프로그램에 참여하는 학생들은 그들의 성적에 더 신경을 쓰거나 그들의 일에 어려움을 겪을 수 있다.이 교란 요인은 튜터링 프로그램과 GPA 사이의 쌍방향 호를 통해 오른쪽에 있는 그림 1-3에 나타나 있다.학생들이 무작위로 기숙사에 배정된다면, 학생의 기숙사와 과외 프로그램과의 거리가 중요한 변수가 될 수 있는 자연스런 후보이다.

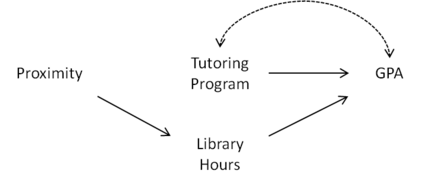
하지만, 만약 과외 프로그램이 대학 도서관에 있다면 어떨까요?이 경우 근접성으로 인해 학생들이 도서관에서 더 많은 시간을 보내게 되고 결과적으로 GPA가 향상될 수 있습니다(그림 1 참조).그림 2의 인과 그래프를 보면 근접도는 G $G_{\overline {X}}$ 의 $G_{\overline {X}}$ $\rightarrow$ {\ $displaystyle$ $\rightarrow$ $\rightarrow$ $}$ 라이브러리 $시간$ $G_{\overline {X}}$ → {\ $displaystyle$ $\$ $rightarrow$ } GPA 경로를 통해 GPA에 연결되므로 계측 변수로 적합하지 않음을 알 수 있습니다 $G_{\overline {X}}$ 단, $다음$ 과 같습니다 $G_{\overline {X}}$ Library Hours에 대한 trol을 공변량으로 추가하면 Proximity가 G $G_{\overline {X}}$ 에서 지정된 Library Hours와 분리되므로 Proximity는 도구 변수가 됩니다. G X ${\$ { \ $style G_{$ \ $overline {$ X} $G_{\overline {X}}$ ^{[citation needed]}} 。

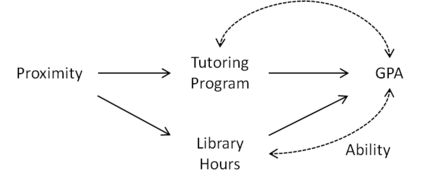
그림 3과 같이 학생의 "자연적 능력"이 도서관에서의 시간뿐만 아니라 학점에 영향을 미친다고 가정해 보자.인과 그래프를 사용하여 라이브러리 시간은 충돌형이며, 라이브러리 시간을 조건부로 설정하면 근접 $→$ $라이브러리$ 시간 $↔$ \ $displaystyle \right$ 화살표 $\leftrightarrow$ $}$ GPA $\rightarrow$ $\leftrightarrow$ 경로가 열립니다.따라서 Proximity를 도구 변수로 사용할 수 없습니다.

마지막으로 도서관에서 공부하지 않는 학생은 그림 4와 같이 다른 곳에서 공부하기 때문에 도서관 시간이 실제로 GPA에 영향을 미치지 않는다고 가정합니다.이 경우 Library Hours를 제어해도 Proximity에서 GPA로의 스플리어스 경로가 열립니다.그러나 라이브러리 시간을 제어하지 않고 공변량으로 제거하면 근접성을 다시 도구 변수를 사용할 수 있습니다.

견적

이제 IV의 메커니즘을 더 자세히 살펴보고 확장합니다.데이터가 형식의 프로세스에 의해 생성된다고 가정합니다.

\displaystyle y_{i}=X_{i}\beta +e_{i}}

어디에

i는 관찰을 색인화합니다.
$(\$ })는 $y_{i}$ 종속 변수의 i번째 값입니다.
$(\$ })는 $X_{i}$ 독립 변수의 i번째 값과 상수 값의 벡터입니다.
$e_{i}$ $X_{i}$ i $(\$ i $e_{i}$ })는 Xi $(\$ $X_{i}$ 의 $(\$ })의 $y_{i}$ 모든 원인을 나타내는 관측되지 않은 오류항의 i번째 값입니다.
$\beta$ β $(\displaystyle\displaystyle)$ 는 $\beta$ 관찰되지 않은 $\beta$ 벡터입니다.

파라미터 $(\displaystyle\beta)$ 는 $\beta$ $X_{i}$ 의 $X_{i}$ 각 요소에서 1개의 단위 변경의 $(\$ $displaystyle$ $y_$ ${i$ 에 $y_{i}$ 대한 인과관계이며 $(\$ })의 $y_{i}$ 다른 모든 원인을 일정하게 유지합니다.계량경제학적 목표는 β $(\displaystyle\beta$ 를 $\beta$ 하는 것이다. 단순성을 위해 e의 추첨은 상관관계가 없으며 동일한 분산의 분포(즉, 오차가 연속적으로 상관관계가 없고 균질하다고 가정한다).

또한 명목적으로 동일한 형태의 회귀 모형이 제안된다고 가정합니다.이 공정에서 얻은 T개 관측치의 랜덤 표본이 주어지면 일반 최소 제곱 추정치는 다음과 같습니다.

{\mathrm {OLS}}=(X^{\mathrm {T}})^{-1}X^{\mathrm {T}}y=(X^{\mathrm {T}X)^{-1}X\mathrm {T

여기서 X, y 및 e는 길이 T의 열 벡터를 나타냅니다.이 방정식은 도입부의 $\operatorname {cov} (X,y)$ θ ( $\operatorname {cov} (X,y)$ , $\operatorname {cov} (X,y)$ ){ $displaystyle \operatorname$ { $cov}(X$ , $y)}$ 과 $\operatorname {cov} (X,y)$ 관련된 방정식과 유사합니다(이것은 이 방정식의 매트릭스 버전입니다).X와 e가 상관 관계가 없는 경우, 특정 규칙성 조건 하에서 두 번째 항은 X를 조건으로 0의 기대값을 가지며 한계에서 0으로 수렴되므로 추정기는 치우치지 않고 일관됩니다.X와 다른 측정되지 않은 경우, e항으로 축소된 원인 변수는 상관관계가 있지만, OLS 추정기는 일반적으로 β에 대해 편향되고 일관성이 없다.이 경우 추정치를 사용하여 주어진 X 값 y의 값을 예측하는 것이 유효하지만 추정치가 Y에 대한 X의 인과 관계를 회복하지는 않습니다.

기본 $\beta$ 변수 $\beta$ β {\displaystyle \ $beta$ 를 복구하기 위해 X의 각 내인성 성분과 높은 상관관계를 가지지만 (기본 모델에서) e와 상관관계가 없는 변수 세트 Z를 도입한다.단순화를 위해 X는 상수의 열과 하나의 내생 변수로 구성된 T × 2 행렬이고, Z는 상수의 열과 하나의 기구 변수로 구성된 T × 2 행렬이라고 생각할 수 있다.단, 이 기술은 X가 상수, 예를 들어 5개의 내생변수로 이루어진 매트릭스이며, Z는 상수와 5개의 기기로 구성된 매트릭스입니다.다음 설명에서는 X가 T × K 행렬이라고 가정하고 이 값 K는 지정되지 않은 상태로 둔다.X와 Z가 모두 T × K 행렬인 추정기를 방금 식별된 행렬이라고 합니다.

각 내생 성분_i x와 기기 사이의 관계가 다음과 같이 주어졌다고 가정합니다.

x_{i}=Z_{i}\gamma +v_{i}

가장 일반적인 IV 규격에서는 다음 추정기를 사용합니다.

{\mathrm {IV}}=(Z^{\mathrm {T}}X)^{-1}Z^{\mathrm {T}}y

이 규격은 실제 모델에서 $Z^{\mathrm {T} }e=0$ $Z^{\mathrm {T} }e=0$ e $Z^{\mathrm {T} }e=0$ {\ $displaystyle$ Z $^{\mathrm {T} }e=0}$ 인 $Z^{\mathrm {T} }e=0$ 한 표본이 커짐에 따라 실제 파라미터에 접근합니다.

{\displaystyle {\mathrm {IV}}=(Z^{\mathrm {T}}X)^{-1}Z^{\mathrm {T}}y=(Z^{\mathrm {T}X)^{-1}Z}+BetA

데이터를 생성하는 기본 프로세스에서 $Z^{\mathrm {T} }e=0$ T $Z^{\mathrm {T} }e=0$ $Z^{\mathrm {T} }e=0$ {\ $displaystyle$ Z $^{\mathrm {T} }e=0}$ 인 $Z^{\mathrm {T} }e=0$ 한 IV 추정기를 적절하게 사용하면 이 매개변수가 식별됩니다.이는 IV가 Z $Z^{\mathrm {T} }e=0$ e $Z^{\mathrm {T} }e=0$ {\ $displaystyle$ Z $^{\mathrm {T} }e=0$ 을(를) 만족하는 고유한 파라미터를 해결하여 샘플 크기가 커짐에 따라 실제 기본 파라미터에 포함되기 때문입니다.

이제 확장: 관심 방정식의 공변량보다 더 많은 계측기가 있다고 가정합니다. 따라서 Z는 M > K인 T × M 행렬입니다.이것은 종종 과잉 식별된 경우라고 불립니다.이 경우 범용 모멘트법(GMM)을 사용할 수 있습니다.GMM IV 추정치는

{{displaystyle {\mathrm {GMM}}=(X^{\mathrm {T}}}P_{Z}X)^{-1}X^{\mathrm {T}}}P_{Z}y,

$P_{Z}$ 서 $({$ 는 $P_{Z}$ 투영 $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ $=$ ( $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ T $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ - $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ T $({$ }= $Z(Z^{\mathrm {T}}Z)^{-1}$ Z^{\ $mathrm$ {T $P_{Z}=Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T} }$ 를 나타냅니다.

이 식은 계측기 수가 관심 방정식의 공변량 수와 같을 때 첫 번째 식으로 축소됩니다.따라서 과잉 식별된 IV는 방금 식별된 IV의 일반화입니다.

방금 확인된 사례에서 β가 β로_IV 붕괴한다는 증거_GMM

$\beta _{\text{GMM}}$ GMM $\beta _{\text{GMM}}$ (\ $style$ \ $beta _{\text{\$ text $})$ $GMM}}}$ 식 $\beta _{\text{GMM}}$ :

{\mathrm {GMM}}=(X^{\mathrm {T}}}Z)^{-1}Z^{\mathrm {T}X)^{-1}X^{-1}Z

방금 확인된 경우에는 공변량만큼 계측기가 있으므로 X의 치수가 Z의 치수와 동일합니다. $X^{\mathrm {T} }Z,Z^{\mathrm {T} }Z$ X $X^{\mathrm {T} }Z,Z^{\mathrm {T} }Z$ Z $X^{\mathrm {T} }Z,Z^{\mathrm {T} }Z$ $X^{\mathrm {T} }Z,Z^{\mathrm {T} }Z$ $X^{\mathrm {T} }Z,Z^{\mathrm {T} }Z$ ${\mathrm {T} Z$ , $Z$ ^ {\ $mathrm$ { $T}$ Z $}$ $Z^{\mathrm {T} }X$ $Z^{\mathrm {T} }X$ T $Z^{\mathrm {T} }X$ X {\ $displaystyle Z^{\mathrm {T}}$ X $Z^{\mathrm {T} }X$ }는 모두 같은 차원의 제곱 행렬이다.모든 가역 n-by-n 행렬 A 및 B에 대해 (AB)⁻¹ = BA라는⁻¹⁻¹ 사실을 사용하여 역행렬을 확장할 수 있습니다(가역 행렬 #속성 참조).

{\displaystyle{\begin{정렬}{\widehat{\beta}}_{\mathrm{GMM}}&=(Z^{\mathrm{T}}X)^ᆳ(Z^{\mathrm{T}}Z)(X^{\mathrm{T}}Z)^{)}X^{\mathrm{T}}Z(Z^{\mathrm{T}}Z)^{)}Z^{\mathrm{T}}y\\&, =(Z^{\mathrm{T}}X)^ᆸ(Z^{\mathrm{T}}Z)(Z^{\mathrm{T}}Z)^{)}Z^{\mathrm{T}}y\\&, =(Z^{\mathrm{T}}X)^{)}Z^{\mathrm{T}}y\\&^{\w.idehat{\beta}}_{\mathrm {IV}}\end {aligned}}}

참고 자료: Davidson and Macinnon(1993)^[13]^{: 218} 참조

m < k의 경우 등가의 과소 식별 추정기가 있다. 매개변수는 선형 방정식 집합에 대한 해이므로 $Z'v=0$ Z $Z'v=0$ v $Z'v=0$ $(\displaystyle$ Z $'v=0)$ 세트를 $Z'v=0$ 사용하는 과소 식별 모델에는 고유한 해법이 없다.

2단계 최소 제곱으로 해석

IV 추정치를 계산하는 데 사용할 수 있는 한 가지 계산 방법은 2단계 최소 제곱(2SLS 또는 TSLS)입니다.첫 번째 단계에서 관심 방정식의 내인성 공변량인 각 설명 변수는 관심 방정식의 외인성 공변량과 제외된 도구를 모두 포함하여 모델의 모든 외인성 변수에 대해 회귀된다.이러한 회귀 분석으로부터 예측치를 얻을 수 있습니다.

스테이지 1: X의 각 열을 Z로 회귀시킨다( $X = Z$ + $X=Z\delta +{\text{errors}}$ {\ $text{delta}$ ） $X=Z\delta +{\text{errors}}$ :

{\mathrm {T}}=(Z^{\mathrm {T}}Z^{\mathrm {T}}X,}

예측값을 저장합니다.

\displaystyle\widehat {X}=Z{\widehat\widehat}=\color {프로세스}Blue}Z(Z^{\mathrm {T} }Z)^{-1}Z^{\mathrm {T}}}X=색상 {프로세스}파란색}P_{Z}}X.,}

두 번째 단계에서는 각 내생적 공변량이 첫 번째 단계의 예측 값으로 대체되는 것을 제외하고, 관심 회귀는 평상시와 같이 추정된다.

2단계: 1단계부터 Y를 예측값으로 회귀시킵니다.

Y=widehat {X}\beta +\mathrm {noise} ,,

그러면

\displaystyle \text{2}SLS}=\left(X^{\mathrm {T}}{\color {Process})파란색}P_{Z}X\right)^{-1}X^{\mathrm {T}}{\color {Process}블루}P_{Z}}Y}

이 방법은 선형 모형에서만 유효합니다.범주형 내인성 공변량의 경우 첫 번째 단계에 대한 프로빗 모형과 두 번째 단계에 대한 OLS와 같은 일반적인 최소 제곱과 다른 첫 번째 단계를 사용하고 싶을 수 있습니다.이는 2단계 IV 모수 추정치가 ^[15]특수한 경우에만 일관되기 때문에 일반적으로 계량학 문헌에서 ^[14]금지 회귀로 알려져 있다.

실증: 2SLS 추정기 계산

일반적인 OLS 추정치는 $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ ( $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ ^ $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ X $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ ) - $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ ^ $({\widehat {X}}^{\mathrm {T} }{\widehat {X}})^{-1}{\widehat {X}}^{\mathrm {T} }Y$ ({\ $wide hat {X}^{\mathrm {T} }$ {\ $wide hat$ {X $})^{-1}$ {\ $wide hat$ {X $}^{\mathrm$ {T $}}$ Y 입니다 ${\widehat {X}}=P_{Z}X$ X X ${\widehat {X}}=P_{Z}X$ ${\widehat {X}}=P_{Z}X$ 를 ${\widehat {X}}=P_{Z}X$ 합니다.P $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ Z $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ Z { $displaystyle P_{Z}^{\mathrm {T}$ } $P_{Z$ } = $P_{Z}$ 가 $P_{Z}^{\mathrm {T} }P_{Z}=P_{Z}P_{Z}=P_{Z}$ 하는 이텐트 매트릭스 $P_{Z}=P_{Z}}$

\displaystyle \text{2}SLS}}=slot\widehat {X}^{\mathrm {T}}{-1}{\widehat {X}{\mathrm {T}}Y=\left(X^{\mathrm {T}}}}P_{Z}{\mathrm {T}}{X}_Z}

β $(\displaystyle\beta)$ 의 $\beta$ 결과 추정치는 위에 표시된 식과 수치적으로 동일합니다. $(\displaystyle \beta)$ 의 $\beta$ 공분산 행렬을 올바르게 계산하려면 2단계 적합 모델의 제곱합 잔차를 약간 보정해야 합니다.

비모수 분석

구조 방정식의 형태를 알 수 없는 경우에도 다음 방정식을 통해 계측 $변수$ Z $(\displaystyle$ Z)를 $Z$ 정의할 수 있습니다.

x=g(z,u),

y=f(x,u),

$f$ 서f { $displaystyle$ f $}$ 와g { $displaystyle$ g $}$ 는 $f$ $g$ 두 개의 임의 $Z$ 이고Z { $displaystyle$ Z $Z$ $}$ 는 U {\ $displaystyle$ U $U$ 와 독립적입니다. 그러나 선형 모델과 달리 $,$ X 및 $(\displaystyle$ Y $)$ $측정$ 에서는 $Z, X$ $평균$ $Y$ 인과 관계를 식별할 수 없습니다.X $(X$ )의 $X$ Y $(Displaystyle$ Y $Y$ ACE로 표시)

디스플레이 스타일ACE}=\Pr(y\mid {text {do}}(x)=\operatorname {E} _{u}[f(x,u)]}

Balke and Pearl[1997]은 ACE의 엄격한 경계를 도출하여 ACE의 ^[16]기호와 크기에 대한 귀중한 정보를 제공할 수 있음을 보여주었다.

선형 분석에서 Z $(\displaystyle$ Z $)$ 가 $Z$ 쌍 $,$ $(X,Y)$ 에 대해 중요한 것으로 가정하는 테스트는 없습니다. 그러나 X $(\displaystyle$ X $)$ 가 $X$ 이산형인 경우에는 그렇지 $않습니다$ .Pearl(2000)은 모든 $f$ {\ $displaystyle$ f $}$ $및$ g {\ $displaystyle$ g $g$ 에 대해Z {\ $displaystyle$ Z $}$ 가 $Z$ 위의 ^[12]두 방정식을 만족할 $Z$ 마다 "계기적 불평등"이라고 불리는 다음 제약 조건을 충족해야 함을 보여 주었다.

\displaystyle \max _{x}\sum _{y}[\max _{z}\Pr(y,x\mid z)]\leq 1.

치료 효과 이질성 하에서의 해석

위의 설명에서는 관심의 인과적 영향이 관찰에 따라 달라지지 않는다고 가정한다. 즉, $\beta$ β(\ $displaystyle \beta)$ 는 $\beta$ $\beta$ 이다.일반적으로 피험자마다 "치료" x의 변화에 대해 다른 방식으로 반응한다. 이 가능성이 인정되면, x의 y 변화 모집단의 평균 효과는 주어진 부분 모집단의 효과와 다를 수 있다.예를 들어, 직업 훈련 프로그램의 평균 효과는 실제로 훈련을 받는 그룹과 훈련을 받지 않기로 선택한 그룹에 따라 크게 다를 수 있습니다.이러한 이유로 IV 방법은 행동 반응에 대한 암묵적 가정, 또는 치료에 대한 반응과 치료를 ^[17]받는 성향 사이의 상관관계에 대한 가정을 호출한다.

표준 IV 추정기는 평균 치료 효과(ATE)^[1]가 아닌 국소 평균 치료 효과(LATE)를 복구할 수 있습니다.Imbens와 Angrist(1994)는 약한 조건에서 선형 IV 추정치를 국소 평균 치료 효과의 가중 평균으로 해석할 수 있으며, 여기서 가중치는 계측 변수의 변화에 대한 내생적 회귀체의 탄성에 의존한다.대략적으로, 이는 변수의 영향이 관측된 계측기의 변화에 의해 영향을 받는 하위 모집단에 대해서만 드러나고 계측기의 변화에 가장 많이 반응하는 하위 모집단이 IV 추정치의 크기에 가장 큰 영향을 미친다는 것을 의미한다.

예를 들어, 연구원이 소득 회귀에서 대학 교육을 위한 수단으로 토지 조성 단과대학의 존재를 사용하는 경우, 그녀는 모집단의 소득에 대한 대학 효과를 파악한다. 모집단은 대학이 있으면 대학 학위를 취득하지만 대학이 없으면 학위를 취득하지 않는다.이러한 경험적 접근은, 더 이상의 가정 없이, 지역 대학이 존재하는지 여부에 관계없이 항상 또는 결코 대학 학위를 취득하지 않을 사람들 사이의 대학 효과에 대해 연구자에게 어떤 것도 말해주지 않는다.

약한 계측기 문제

Bound, Jaeger 및 Baker(1995년)가 지적했듯이, 문제는 1단계 ^[18]방정식에서 내생적 질문 예측 변수의 빈약한 예측 변수인 "약한" 계측기를 선택함으로써 발생한다.이 경우 계측기에 의한 질문 예측 변수의 예측은 빈약하고 예측 값의 변동은 거의 없습니다.결과적으로, 2단계 방정식의 질문 예측 변수를 대체하기 위해 사용될 때, 최종 결과를 예측하는 데 큰 성공을 거두지 못할 것 같다.

위에서 논의한 흡연과 건강 사례의 맥락에서, 흡연 상태가 세금 변화에 대부분 반응하지 않는다면, 담배세는 흡연에 대한 약한 수단이다.만약 높은 세금이 사람들로 하여금 담배를 끊도록 유도하지 않는다면, 세율의 변화는 우리에게 흡연이 건강에 미치는 영향에 대해 아무것도 말해주지 않는다.세금이 흡연에 미치는 영향이 아닌 다른 경로를 통해 건강에 영향을 미치는 경우, 해당 상품은 무효이며, 수단 변수 접근법은 잘못된 결과를 초래할 수 있다.예를 들어, 상대적으로 건강에 관심이 있는 인구가 많은 장소나 시간대는 높은 담뱃세를 부과하고 흡연율을 일정하게 유지해도 더 건강해질 수 있기 때문에 흡연이 건강에 영향을 주지 않는다고 해도 건강세와 담뱃세의 상관관계를 관찰할 수 있다.이 경우 담배세와 건강의 상관관계에서 흡연이 건강에 미치는 인과관계를 추론하는 것은 잘못이다.

약한 기기 테스트

내생 공변량과 계측기가 모두 관측 ^[19]가능하기 때문에 계측기의 강도를 직접 평가할 수 있습니다.단일 내인성 회귀 분석기가 있는 모델에 대한 일반적인 경험 규칙은, 1단계 회귀 분석에서 제외된 계측기가 무관하다는 Null에 대한 F-통계치는 10보다 커야 한다는 것이다.

통계적 추론 및 가설 검정

공변량이 외생적인 경우 X를 조건으로 추정기의 모멘트를 계산하여 OLS 추정기의 소표본 속성을 간단한 방법으로 도출할 수 있습니다.일부 공변량이 내생적이어서 도구 변수 추정이 구현되면 추정기의 모멘트에 대한 간단한 식을 얻을 수 없습니다.일반적으로 계측 변수 추정기는 유한 표본이 아닌 바람직한 점근적 특성만 가지며 추론은 추정기의 표본 분포에 대한 점근적 근사치를 기반으로 합니다.계측기가 관심 방정식의 오류와 상관관계가 없고 계측기가 약하지 않은 경우에도 계측 변수 추정기의 유한 표본 특성은 불량할 수 있다.예를 들어 정확하게 식별된 모형은 모멘트가 없는 유한 표본 추정기를 생성하므로 추정기는 편향되지도 않고 편향되지도 않으며 검정 통계량의 공칭 크기가 상당히 왜곡될 수 있으며 추정치는 일반적으로 ^[20]모수의 실제 값과 멀리 떨어져 있을 수 있다.

제외 제한 테스트

계측기가 관심 방정식의 오차항과 상관 관계가 없다는 가정은 정확히 식별된 모형에서는 검정할 수 없습니다.모형이 과대 식별된 경우 이 가정을 검정하는 데 사용할 수 있는 정보가 있습니다.사르간-한센 검정이라고 불리는 이러한 과잉 식별 제한에 대한 가장 일반적인 검정은 계측기가 정말로 ^[21]외생적인 경우 잔차가 외생 변수 집합과 상관관계가 없어야 한다는 관찰에 기초한다.사르간-한센 검정 통계량은 잔차의 OLS 회귀에서 외생 변수 집합으로 T $TR^{2}$ ({ $displaystyle$ TR $^{2}})($ 관측치에 결정 계수를 곱한 수)로 계산할 수 있다.이 통계량은 오차항이 계측기와 상관되지 않는다는 null 아래의 m - k 자유도와 점근적으로 카이 제곱됩니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Imbens, G.; Angrist, J. (1994). "Identification and estimation of local average treatment effects". Econometrica. 62 (2): 467–476. doi:10.2307/2951620. JSTOR 2951620. S2CID 153123153.
^ Bullock, J. G.; Green, D. P.; Ha, S. E. (2010). "Yes, But What's the Mechanism? (Don't Expect an Easy Answer)". Journal of Personality and Social Psychology. 98 (4): 550–558. CiteSeerX 10.1.1.169.5465. doi:10.1037/a0018933. PMID 20307128. S2CID 7913867.
^ https://www.stata.com/meeting/5nasug/wiv.pdf^{[인용필수]}
^ Nichols, Austin (2006-07-23). "Weak Instruments: An Overview and New Techniques". {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ Epstein, Roy J. (1989). "The Fall of OLS in Structural Estimation". Oxford Economic Papers. 41 (1): 94–107. doi:10.1093/oxfordjournals.oep.a041930. JSTOR 2663184.
^ Stock, James H.; Trebbi, Francesco (2003). "Retrospectives: Who Invented Instrumental Variable Regression?". Journal of Economic Perspectives. 17 (3): 177–194. doi:10.1257/089533003769204416.
^ Reiersøl, Olav (1945). Confluence Analysis by Means of Instrumental Sets of Variables. Arkiv for Mathematic, Astronomi, och Fysik. Vol. 32A. Uppsala: Almquist & Wiksells. OCLC 793451601.
^ 울드리지, J:계량 입문남서부, 스카버러, 카나다, 2009년
^ Bowden, R.J.; Turkington, D.A. (1984). Instrumental Variables. Cambridge, England: Cambridge University Press.
^ Leigh, J. P.; Schembri, M. (2004). "Instrumental Variables Technique: Cigarette Price Provided Better Estimate of Effects of Smoking on SF-12". Journal of Clinical Epidemiology. 57 (3): 284–293. doi:10.1016/j.jclinepi.2003.08.006. PMID 15066689.
^ Angrist, J.; Krueger, A. (2001). "Instrumental Variables and the Search for Identification: From Supply and Demand to Natural Experiments". Journal of Economic Perspectives. 15 (4): 69–85. doi:10.1257/jep.15.4.69.
^ ^a ^b ^c Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press. ISBN 978-0-521-89560-6.
^ Davidson, Russell; Mackinnon, James (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. ISBN 978-0-19-506011-9.
^ 울드리지, J. (2010)단면 및 패널 데이터의 계량 분석.단면 및 패널 데이터의 계량 분석.MIT ^{[page needed]}프레스
^ Lergenmuller, Simon (2017). Two-stage predictor substitution for time-to-event data (Thesis). hdl:10852/57801.
^ Balke, A.; Pearl, J. (1997). "Bounds on treatment effects from studies with imperfect compliance". Journal of the American Statistical Association. 92 (439): 1172–1176. CiteSeerX 10.1.1.26.3952. doi:10.1080/01621459.1997.10474074. S2CID 18365761.
^ Heckman, J. (1997). "Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations". Journal of Human Resources. 32 (3): 441–462. doi:10.2307/146178. JSTOR 146178.
^ Bound, J.; Jaeger, D. A.; Baker, R. M. (1995). "Problems with Instrumental Variables Estimation when the Correlation between the Instruments and the Endogenous Explanatory Variable is Weak". Journal of the American Statistical Association. 90 (430): 443. doi:10.1080/01621459.1995.10476536.
^ Stock, J.; Wright, J.; Yogo, M. (2002). "A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments". Journal of the American Statistical Association. 20 (4): 518–529. CiteSeerX 10.1.1.319.2477. doi:10.1198/073500102288618658. S2CID 14793271.
^ Nelson, C. R.; Startz, R. (1990). "Some Further Results on the Exact Small Sample Properties of the Instrumental Variable Estimator". Econometrica. 58 (4): 967–976. doi:10.2307/2938359. JSTOR 2938359. S2CID 119872226.
^ Hayashi, Fumio (2000). "Testing Overidentifying Restrictions". Econometrics. Princeton: Princeton University Press. pp. 217–221. ISBN 978-0-691-01018-2.

추가 정보

Greene, William H. (2008). Econometric Analysis (Sixth ed.). Upper Saddle River: Pearson Prentice-Hall. pp. 314–353. ISBN 978-0-13-600383-0.
Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 711–736. ISBN 978-0-07-337577-9.
Sargan, Denis (1988). Lectures on Advanced Econometric Theory. Oxford: Basil Blackwell. pp. 42–67. ISBN 978-0-631-14956-9.
Wooldridge, Jeffrey M. (2013). Introductory Econometrics: A Modern Approach (Fifth international ed.). Mason, OH: South-Western. pp. 490–528. ISBN 978-1-111-53439-4.

참고 문헌

Woldridge, J. (1997):계수 데이터에 대한 준우도 방법, 응용 계량 핸드북, 제2권, ED. H. 페사란 및 P.슈미트, 옥스퍼드, 블랙웰, 페이지 352-406
Terza, J. V.(1998): "내생 스위칭에 의한 카운트 모델 추정: 샘플 선택과 내생 치료 효과"계량경제학 저널(84), 129–154페이지
Woldridge, J. (2002) :MIT Press, 매사추세츠, 캠브리지, "단면 및 패널 데이터의 계량 분석"

외부 링크

대니얼 맥패든의 교과서 장
Mark Thoma의 YouTube에서의 계량경제학 강의(주제: 도구 변수)
Mark Thoma의 YouTube에서의 계량경제학 강의(주제: 2단계 최소 제곱)

[Imbens:00-1] Imbens, G.; Angrist, J. (1994). "Identification and estimation of local average treatment effects". Econometrica. 62 (2): 467–476. doi:10.2307/2951620. JSTOR 2951620. S2CID 153123153.

[Bullock:00-2] Bullock, J. G.; Green, D. P.; Ha, S. E. (2010). "Yes, But What's the Mechanism? (Don't Expect an Easy Answer)". Journal of Personality and Social Psychology. 98 (4): 550–558. CiteSeerX 10.1.1.169.5465. doi:10.1037/a0018933. PMID 20307128. S2CID 7913867.

[3] ttps://www.stata.com/meeting/5nasug/wiv.pdf^{[인용필수]}

[4] Nichols, Austin (2006-07-23). "Weak Instruments: An Overview and New Techniques". {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[5] Epstein, Roy J. (1989). "The Fall of OLS in Structural Estimation". Oxford Economic Papers. 41 (1): 94–107. doi:10.1093/oxfordjournals.oep.a041930. JSTOR 2663184.

[stock:trebbi03-6] Stock, James H.; Trebbi, Francesco (2003). "Retrospectives: Who Invented Instrumental Variable Regression?". Journal of Economic Perspectives. 17 (3): 177–194. doi:10.1257/089533003769204416.

[7] Reiersøl, Olav (1945). Confluence Analysis by Means of Instrumental Sets of Variables. Arkiv for Mathematic, Astronomi, och Fysik. Vol. 32A. Uppsala: Almquist & Wiksells. OCLC 793451601.

[Wool-8] 울드리지, J:계량 입문남서부, 스카버러, 카나다, 2009년

[bowden:turkington84-9] Bowden, R.J.; Turkington, D.A. (1984). Instrumental Variables. Cambridge, England: Cambridge University Press.

[Leigh:00-10] Leigh, J. P.; Schembri, M. (2004). "Instrumental Variables Technique: Cigarette Price Provided Better Estimate of Effects of Smoking on SF-12". Journal of Clinical Epidemiology. 57 (3): 284–293. doi:10.1016/j.jclinepi.2003.08.006. PMID 15066689.

[angrist:00-11] Angrist, J.; Krueger, A. (2001). "Instrumental Variables and the Search for Identification: From Supply and Demand to Natural Experiments". Journal of Economic Perspectives. 15 (4): 69–85. doi:10.1257/jep.15.4.69.

[Pearl:00-12] Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press. ISBN 978-0-521-89560-6.

[13] Davidson, Russell; Mackinnon, James (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. ISBN 978-0-19-506011-9.

[14] 울드리지, J. (2010)단면 및 패널 데이터의 계량 분석.단면 및 패널 데이터의 계량 분석.MIT ^{[page needed]}프레스

[15] Lergenmuller, Simon (2017). Two-stage predictor substitution for time-to-event data (Thesis). hdl:10852/57801.

[balke:pearl97-16] Balke, A.; Pearl, J. (1997). "Bounds on treatment effects from studies with imperfect compliance". Journal of the American Statistical Association. 92 (439): 1172–1176. CiteSeerX 10.1.1.26.3952. doi:10.1080/01621459.1997.10474074. S2CID 18365761.

[17] Heckman, J. (1997). "Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations". Journal of Human Resources. 32 (3): 441–462. doi:10.2307/146178. JSTOR 146178.

[18] Bound, J.; Jaeger, D. A.; Baker, R. M. (1995). "Problems with Instrumental Variables Estimation when the Correlation between the Instruments and the Endogenous Explanatory Variable is Weak". Journal of the American Statistical Association. 90 (430): 443. doi:10.1080/01621459.1995.10476536.

[Stock:00-19] Stock, J.; Wright, J.; Yogo, M. (2002). "A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments". Journal of the American Statistical Association. 20 (4): 518–529. CiteSeerX 10.1.1.319.2477. doi:10.1198/073500102288618658. S2CID 14793271.

[Nelson_1990:00-20] Nelson, C. R.; Startz, R. (1990). "Some Further Results on the Exact Small Sample Properties of the Instrumental Variable Estimator". Econometrica. 58 (4): 967–976. doi:10.2307/2938359. JSTOR 2938359. S2CID 119872226.

[21] Hayashi, Fumio (2000). "Testing Overidentifying Restrictions". Econometrics. Princeton: Princeton University Press. pp. 217–221. ISBN 978-0-691-01018-2.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[15]

[14]

[16]

[17]

[18]

[19]

[20]

[21]

Search

계측 변수 추정

네임스페이스

더

목차

역사

이론.

예

그래픽 정의

적합한 기기 선택

견적

2단계 최소 제곱으로 해석

비모수 분석

치료 효과 이질성 하에서의 해석

약한 계측기 문제

약한 기기 테스트

통계적 추론 및 가설 검정

제외 제한 테스트

「」를 참조해 주세요.

레퍼런스

추가 정보

참고 문헌

외부 링크

Search

계측 변수 추정

역사

이론.

예

그래픽 정의

적합한 기기 선택

견적

2단계 최소 제곱으로 해석

비모수 분석

치료 효과 이질성 하에서의 해석

약한 계측기 문제

약한 기기 테스트

통계적 추론 및 가설 검정

제외 제한 테스트

「 」를 참조해 주세요.

레퍼런스

추가 정보

참고 문헌

외부 링크

「」를 참조해 주세요.