가로 메르카토르 투영법

가로 메르카토르 지도 투영은 표준 메르카토르 투영을 개작한 것이다. 가로판은 만국횡단 메르카토르를 비롯한 전 세계 국가 및 국제 지도 시스템에서 널리 사용되고 있다. 적절한 측지 측지 기준과 쌍을 이루면 횡방향 메르카토르는 동서 범위에서 몇 도 미만의 구역에서 높은 정확도를 전달한다.

표준면 및 가로면

횡방향 메르카토르 투영은 표준(또는 일반) 메르카토르 투영의 횡단면이다. 이들은 동일한 기초 수학 구조를 공유하며, 결과적으로 가로 메르카토르는 일반 메르카토르로부터 많은 특성을 물려받는다.

• 두 투영 모두 원통형이다. Normal Mercator의 경우 실린더의 축은 극축과 적도와의 접선선과 일치한다. 횡단 메르카토르의 경우 실린더의 축이 적도면에 위치하며, 접선의 선은 선택된 자오선이라 하여 중심 자오선을 지정하였다.
• 두 투영 모두 제2의 형태로 수정될 수 있으며, 이는 저울이 축소되어 원통이 모델 지구본을 통과하도록 함을 의미한다.
• 둘 다 구형과 타원형 버전에서 존재한다.
• 두 투영 모두 일치하므로 점 척도가 방향과 독립적이며 국소 모양이 잘 보존된다.
• 두 투영 모두 접선(정상 메르카토르의 적도와 횡단의 중심 자오선)에 일정한 척도를 가지고 있다.

가로 메르카토르의 중심 자오선을 마음대로 선택할 수 있기 때문에 지구상의 어느 곳에서도 (좁은 폭의) 매우 정확한 지도를 제작하는 데 사용할 수 있다. 가로 메르카토르(Mercator)의 세컨트 타원형(secant, 타원형)은 정확한 대규모 지도를 위해 모든 투영 중에서 가장 광범위하게 적용된다.

구면 횡축 메르카토르

어떤 투영에 지도를 만들 때, 지도된 영역의 범위가 양차원에서 수백 km를 초과할 때, 일반적으로 지구를 모형화하기 위해 구를 선택한다. 더 작은 영역의 지도에서 더 높은 정확도가 필요한 경우 타원형 모델을 선택해야 한다. 다음 섹션을 참조하십시오. 가로 메르카토르 투영법의 구형은 요한 하인리히 램버트가 1772년에 제시한 7개의 새로운 투영법들 중 하나이다.^[1][2] (본문은 현대 영어 번역으로도 볼 수 있다.)^[3] 램버트는 그의 예상에 이름을 붙이지 않았다; 메르카토르라는 이름은 19세기 후반부터 유래되었다.^[4] 가로 투영의 주요 특성은 일반 투영의 특성과 비교하여 여기에 제시된다.

정규 및 횡단 구면 투영

타립소달 횡축 메르카토르

가로 메르카토르 투영의 타원형 형태는 1825년^[5] 칼 프리드리히 가우스에 의해 개발되었고, 1912년 요한 하인리히 루이 크뤼거에 의해 추가로 분석되었다.^[6]

투영법은 미국의 메르카토르 횡단 (엘리프소이달); 유럽의 가우스 컨포멀 또는 가우스-크뤼거; 또는 가우스-크뤼거 횡단 메르카토르 횡단 (Gauss-Krüger) 등 여러 이름으로 알려져 있다. 타원형 횡방향 메르카토르 지도 투영에 대한 동의어 외에 가우스-크뤼거라는 용어는 약간 다른 방법으로 사용될 수 있다.

• 때때로 이 용어는 Mercator 가로에 대한 특정한 계산 방법, 즉 위도/경도와 투영 좌표 사이에서 변환하는 방법에 사용된다. 지구가 타원체로 모델링될 때 그렇게 하는 단순한 폐쇄 공식은 없다. 그러나 가우스-크뤼거 방법은 적어도 중심 자오선 부근에 충분히 있는 경우, 즉 경도 100도 미만의 다른 방법과 동일한 결과를 준다. 더 멀리, 어떤 방법들은 부정확해진다.
• 이 용어는 또한 적어도 독일, 터키, 오스트리아, 슬로베니아, 크로아티아, 보스니아-헤르체고비나, 세르비아, 몬테네그로, 북마케도니아, 핀란드, 아르헨티나에서, 유럽과 남아메리카의 좁은 지역에서 사용되는 특정한 일련의 메르카토르 돌출부에도 사용된다. 이 가우스-크뤼거 시스템은 범용 횡단 메르카토르 시스템과 유사하지만 가우스-크뤼거 구역의 중심 경맥은 UTM의 6°와는 달리 3°밖에 차이가 나지 않는다.

투영은 중심 자오선에 일정한 척도로 일치한다.(구체에서 타원체까지 횡단 메르카토르의 다른 등정 일반화가 있지만 중심 자오선에는 가우스-크뤼거만이 일정한 척도를 가지고 있다) 20세기에 걸쳐 가우스-크뤼거 횡단 메르카토르는 여러 국가(및 국제 기구)에 의해 어떤 형태로든 채택되었다.^[7] 또한 그것은 범용 횡단 메르카토르 일련의 예측에 대한 기초를 제공한다. 가우스-크뤼거 투영은 현재 정확한 대규모 매핑에서 가장 널리 사용되는 투영법이다.^{[citation needed]}

가우스와 크뤼거에 의해 개발된 이 투영은 구면 버전에서와 정확히 같이 동서로 분화한다고 가정된 저순위의 동력계열로 표현되었다. 1976년 L. P. Lee가 보고한 정확한 (폐쇄형) 투영본의 미발표 버전인 영국의 지도제작자 E. H. 톰슨은 타원형 투영이 유한(아래)임을 보여 주었다.^[8] 이것은 가로 메르카토르 투영법의 구형과 타원형 투영법 사이의 가장 현저한 차이점이다: 가우스-크뤼거는 중심 자오선에 대한 "접근"을 정밀하게 표시하는 것이 주된 응용이지만 전체 타원체를 평면에 합리적으로 투영하는 것이다.^{[citation needed]}

특징들

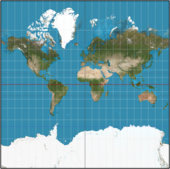
• 중심 자오선 부근(위의 예에서 그리니치)에서는 돌출부의 왜곡이 적고 아프리카, 서유럽, 영국 섬, 그린란드, 남극의 형상이 지구와 비교가 잘 된다.
• 구면 투영과 타원체의 횡단 투영의 중심 영역은 여기에 표시된 작은 규모의 투영에서 구별할 수 없다.
• 선택된 중심 자오선의 동서로 90°에 있는 경맥들은 극을 통해 수평선에 투영된다. 더 먼 반구는 북극 위와 남극 아래에 투영된다.
• 적도는 아프리카를 이등분하고 남아메리카를 가로지른 다음 투영의 완전한 바깥 경계까지 계속된다. 위와 아래 가장자리와 오른쪽과 왼쪽 가장자리는 반드시 식별되어야 한다(즉, 지구상에서 동일한 선을 나타낸다). (인도네시아는 이등분되어 있다.)
• 왜곡은 투영의 좌우 경계를 향해 증가하지만 무한대로 증가하지는 않는다. 왼쪽 하단에서 90° 서경 자오선과 적도가 만나는 갈라파고스 섬에 주목하십시오.
• 지도는 일치한다. 타원형 프로젝트에서 지정된 각도에서 교차하는 선과 투영에서 동일한 각도에서 교차하는 선입니다. 특히 평행과 경맥은 90°에서 교차한다.
• 점 척도 계수는 어느 지점에서 방향과 독립적이어서 작은 지역의 형상이 합리적으로 잘 보존된다. 필요한 조건은 해당 지역에 걸쳐 규모 인자의 크기가 너무 크게 달라서는 안 된다는 것이다. 남아메리카는 크게 왜곡되어 있지만 실론섬은 중심 자오선으로부터 멀리 떨어져 있음에도 불구하고 합리적으로 형성될 만큼 작다는 점에 유의한다.
• 중심 자오선의 선택은 투영의 모양에 큰 영향을 미친다. 90°W를 선택하면 아메리카 대륙 전체가 합리적이다. 145°E를 선택하면 극동이 좋고 호주는 북향이다.

대부분의 적용에서 가우스-크뤼거 좌표계는 구면과 타원형 버전의 차이는 작지만 정확한 매핑에 중요한 중심 경혈 근처의 좁은 스트립에 적용된다. 척도, 수렴 및 왜곡에 대한 직계 열은 타원체 위도와 경도의 함수다. 역계열은 편심 함수와 투영에서 모두 x와 y의 함수다. 2차 버전에서 투영된 실제 척도의 선은 더 이상 중심 자오선에 평행하지 않고 약간 휘어져 있다. 투영된 경혈과 x 상수 격자선 사이의 수렴각은 더 이상 0이 아니므로(적도를 제외하고) 진정한 북쪽으로부터 방위각을 얻기 위해 격자 베어링을 교정해야 한다. 그 차이는 작지만, 특히 높은 위도에서 무시할 수는 없다.

Gauss-Kruger 투영법 구현

크뤼거는^[6] 1912년 논문에서 두 가지 뚜렷한 해결책을 제시했는데, 여기서 확장 매개변수로 구별된다.

• 크뤼거-n (5~8항): 좌표를 x와 y로 하는 직접 투영을 위한 공식은 세 번째 평탄화, n(타원체의 주축과 부축의 차이와 합계의 비율) 측면에서 네 번째 순서 확장이다. 계수는 위도(위도), 경도(경도), 주축(a) 및 편심(e) 단위로 표현된다. φ과 λ에 대한 역 공식도 n의 네 번째 순서 확장이지만 x, y, a, e 단위로 계수가 표현된다.
• 크뤼거-제13항과 제14항: 투영 좌표 x와 y를 주는 공식은 경도 λ의 관점에서 확장(각각 순서 5와 4)이며, 라디안으로 표현된다: 계수는 φ, a, e의 단위로 표현된다. φ과 λ의 역투영법은 비율에 있어 여섯 번째 순서 확장이다. x/a, 계수가 y, a 및 e 단위로 표현됨(횡단 메르카토르: Redfearn 시리즈 참조)

Krüger-them 시리즈는 가장 먼저 시행되었는데, 아마도 20세기 중반의 수동 계산기로 평가하는 것이 훨씬 쉬웠기 때문일 것이다.

• 리-레드펀-OSGB: 1945년 L. P. 리는^[9] 크루거의 확장을 확인하고 OSGB에 의해^[10] 채택을 제안했지만, 레드펀(1948)은 ^[11](a) 영국의 상대적으로 높은 위도와 (b) 10도가 넘는 지도상의 넓은 넓이 때문에 정확하지 않다고 지적했다. Redfearn은 시리즈를 8번째 순서로 확장하고 1mm의 정확도를 얻기 위해 필요한 항(지면 측정)을 조사했다. Redfearn 시리즈는 여전히 OSGB 지도 예측의 기초가 된다.^[10]
• 토마스-UTM: 크뤼거의 팽창은 1952년 폴 토마스(^[13]Paul Thomas)에 의해 확인되었는데, ^[12]스나이더(Snyder)에서는 쉽게 구할 수 있다. 레드펜이 제시한 것과 완전히 동등한 그의 투영 공식은 미국 국방지도국에 의해 UTM의 근거로 채택되었다.^[14] 그것들은 또한 미국 국립 지리공간정보국이 이용할 수 있도록 만든 지오트란스^[15] 좌표 변환기에 통합되어 있다[3].
• 기타 국가: Redfearn 시리즈는 많은 국가에서 측지학적 매핑의 기초가 된다. 호주, 독일, 캐나다, 남아공, 몇 개만 언급할 것. (목록은 Stuifbergen 2009의 부록 A.1에 제시되어 있다.)^[16]
• 레드펀 시리즈의 많은 변종들이 제안되었지만 국가 지도 기관에서 채택한 변종들만 중요하다. 이 상태가 아닌 수정의 예는 횡축 메르카토르: Bowring 시리즈)를 참조하십시오. 이러한 모든 수정은 현대 컴퓨터의 파워와 아래에 요약된 고차 n 시리즈 개발로 인해 생략되었다. 정밀한 레드펀 시리즈는 비록 순서가 낮지만 OSGB, UTM 등의 준법적 정의에 여전히 담겨 있기 때문에 무시할 수 없다.

크뤼거-n 시리즈는 다음 국가들에 의해 (n의 네 번째 순서로) 이행되었다.

• 프랑스^[17]
• 핀란드^[18]
• 스웨덴^[19]
• 일본^[20]

크뤼거-n 시리즈의 고차 버전은 엔사게르와 포더가^[21] 7번째 순서로, 카와세가 10번째 순서로 이행했다.^[22] 위도와 등위도의 변형을 위한 시리즈 확장과는 별도로 카니는 시리즈를 30번째 순서로 구현했다.^[23]

정확한 가우스-크뤼거 및 절단 시리즈의 정확도

E. H. 톰슨의 정확한 해결책은 L. P. Lee에 의해 설명된다.^[8] 타원함수(NIST^[24] 핸드북 19장과 22장에서 정의)의 관점에서 구성되는데, 맥시마와 같은 대수적 계산 시스템을 사용하여 임의의 정확도로 계산할 수 있다.^[25] 이와 같은 정확한 해결책의 구현은 카니(2011년)가 기술하고 있다.^[23]

정확한 용액은 잘린 n과 λ 시리즈의 정확도를 평가하는 데 귀중한 도구다. 예를 들어, 원래의 1912년 크뤼거-n 시리즈는 정확한 값과 매우 유리하게 비교된다. 즉, 중심 자오선의 1000km 이내에서 0.31μm 미만으로, 그리고 6,000km에서 1mm 미만으로 차이가 난다. 반면, Geotrans가 사용하는 Redfearn 시리즈와 정확한 용액의 차이는 1 mm에서 3도의 경도 차이에 이르며, 적도의 중심 자오선으로부터 334 km 떨어져 있지만 UTM 구역의 북방한계에서는 35 km에 불과하다. 따라서 크뤼거-n 시리즈는 레드펀 λ 시리즈보다 훨씬 낫다.

레드펀 시리즈는 구역이 넓어질수록 훨씬 더 나빠진다. 카니는 그린랜드에 대해 교훈적인 예로 논한다. 길고 얇은 육지 질량은 42W에 집중되며, 가장 넓은 지점에서 경도의 범위가 거의 50도에 이르는 동안 경도로부터 750km 이상 떨어져 있지 않다. 크뤼거-n은 1mm 이내로 정확하지만, 크뤼거-시퀀스 시리즈의 레드펜 버전은 최대 1km의 오차를 가진다.

카니가 자체 개발한 8차(n) 시리즈는 중심 자오선의 3900km 이내에서 5nm까지 정확하다.

구면횡 메르카토르 공식

구면 정상 메르카토르 재방문

일반적인 원통형 돌출부는 구의 극축을 따라 축이 있는 적도의 원통 접선을 기준으로 설명된다. 원통형 돌출부는 자오선의 모든 점이 x = aλ 및 y의 규정된 함수인 지점에 투영되도록 구성된다. 접선 Normal Mercator 투영의 경우, 일치성을 보장하는 (유일) 공식은 다음과 같다.^[26]

${\displaystyle x=a\lambda \,,\qquad y=a\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right]={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right].}$

일치성은 점 척도 k가 방향과 무관하다는 것을 의미한다: 그것은 위도의 함수일 뿐이다:

${\displaystyle k(\varphi )=\sec \varphi .\,}$

투영의 2차 버전의 경우, 이 모든 방정식의 오른쪽에₀ k의 인수가 있다. 이것은 적도에서 척도가 k와₀ 동일함을 보장한다.

정규 및 횡단 격자

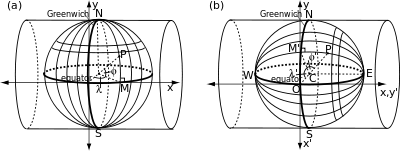
왼쪽의 그림은 가로 실린더가 구의 전통적인 눈금과 어떻게 관련이 있는지를 보여준다. 그것은 임의로 선택된 몇몇 자오선과 접하고 그것의 축은 구의 자오선과 수직이다. 그림에 정의된 x축과 y축은 적도와 중심 자오선과 정확히 연관되어 있으며, 정상 투영과 동일하다. 오른쪽 그림에서 회전 눈금은 일반 실린더가 표준 눈금에 관련된 것과 같은 방식으로 횡단 실린더와 관련된다. 회전된 눈금의 '동등', '폴레'(E와 W), '메리디아인'은 선택된 중심 자오선, 중심 자오선 동쪽과 서쪽 90도의 적도에 있는 점, 그리고 그 지점을 통과하는 원형으로 식별된다.

표준 눈금에 대한 임의 점(φ, λ)의 위치도 회전 눈금의 각도에서 확인할 수 있다: φ′(각도 M′CP)는 유효 위도이고 -λ′(각도 M′CO)는 유효 경도가 된다. (마이너스 부호는 (φ′,λ′)이 ( gr,λ)이 표준 눈금과 관계되는 것과 같은 방법으로 회전 눈금에 관련되도록 필요하다. 카르테시안(x′,y′) 축은 축(x,y) 축이 표준 눈금에 관계되는 것과 같은 방식으로 회전된 눈금에 관련된다.

접선 횡방향 메르카토르 투영은 접선 일반 메르카토르 투영의 변환 공식에 의해 좌표(x′,y′)를 -λ′ 및 φ′ 단위로 정의한다.

${\displaystyle x'=-a\a\qquad y'={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi '}}{1-\sin \varphi '}}}\right].}$

이 변환은 중심 자오선을 유한 길이의 직선으로 투영하는 동시에 E와 W(적도를 포함)를 통해 대원(大原)을 중심 자오선에 수직인 무한 직선으로 투영한다. 진정한 평행과 경맥(적도와 중심 자오선 제외)은 회전하는 눈금에 단순한 관계가 없으며 복잡한 곡선을 투영한다.

결절 사이의 관계

두 격자의 각도는 원점을 통하여 참 자오선에 의해 정의된 구형 삼각형 NM meridianP에 구면 삼각형 NM′P, 임의점을 통한 참 자오선, MPN, 대원 WM′PE를 사용하여 관련된다. 결과는 다음과 같다.^[26]

${\displaystyle {\regated}\sin \varphi '&=\sin \sin \coses \varphi,\\tan \varpi '&=\sec \tan \varphi.\ended}}}}}$

직접변환식

데카르트 좌표(x,y)를 제공하는 직접 공식은 위에서부터 바로 이어진다. x = y′ 및 y = -x′(및 secant 버전을 수용하도록 k의₀ 요인 복원)

${\displaystyle {\begin{aligned}x(\lambda ,\varphi )&={\frac {1}{2}}k_{0}a\ln \left[{\frac {1+\sin \lambda \cos \varphi }{1-\sin \lambda \cos \varphi }}\right],\\[5px]y(\lambda ,\varphi )&=k_{0}a\arctan \left[\sec \lambda \tan \varphi \right],\end{aligned}}}$

위의 표현은 램버트(Lambert^[1])와 스나이더(^[13]Snyder), 말링(Maling^[27]), 오스본^[26](Osborn)에서도 제시된다.

역변환식

위의 방정식을 뒤집으면 다음과 같은 결과를 얻을 수 있다.

${\displaystyle {\begin{aligned}\lambda (x,y)&=\arctan \left[\sinh {\frac {x}{k_{0}a}}\sec {\frac {y}{k_{0}a}}\right],\\[5px]\varphi (x,y)&=\arcsin \left[{\mbox{sech}}\;{\frac {x}{k_{0}a}}\sin {\frac {y}{k_{0}a}}\right].\end{정렬}}}$

점 척도

회전 눈금에 대한 좌표 측면에서 점 척도 계수는 k = sec ′′로 주어진다. 이는 지리적 좌표 또는 투영 좌표의 측면에서 표현될 수 있다.

${\displaystyle {\begin{aligned}k(\lambda ,\varphi )&={\frac {k_{0}}{\sqrt {1-\sin ^{2}\lambda \cos ^{2}\varphi }}},\\[5px]k(x,y)&=k_{0}\cosh \left({\frac {x}{k_{0}a}}\right).\end{정렬}}}$

두 번째 표현은 축척 인자가 투영의 중심 자오선으로부터 거리의 함수일 뿐이라는 것을 보여준다. 축척 인자의 일반적인 값은 k₀ = 0.9996이므로 x가 약 180 km일 때 k = 1이다. x가 약 255km이고₀ k = 1.0004인 경우: 스케일 계수는 약 510km 폭의 스트립에서 0.04%의 균일성 내에 있다.

수렴

투영 지점의 수렴각 γ은 진실 북부를 정의하는 투영 자오선으로부터 상수 x의 격자선까지 측정한 각도로 정의되며, 그리드는 북쪽을 정의한다. 따라서 γ은 적도의 북쪽 사분면과 중심 자오선의 동쪽, 적도의 남쪽과 중심 자오선의 서쪽 사분면에 양성이 있다. 정합성은 그리드 베어링에 추가되어야 진정한 북쪽으로부터 베어링을 얻을 수 있다. Secant 횡방향 Mercator의 경우 수렴은 지리적 좌표 또는 투영 좌표 중 하나로 표현될^[26] 수 있다.

${\displaystyle {\begin{aligned}\gamma (\lambda ,\varphi )&=\arctan(\tan \lambda \sin \varphi ),\\[5px]\gamma (x,y)&=\arctan \left(\tanh {\frac {x}{k_{0}a}}\tan {\frac {y}{k_{0}a}}\right).\end{정렬}}}$

타원형 횡축 메르카토르 공식

실제 구현 상세 내역

• 가우스-크루거 시리즈(경도): 횡축 메르카토르: 레드펜 시리즈
• 가우스-크루거 시리즈(n)(세 번째 평탄화): 횡축 메르카토르: 직렬 평탄화
• 정확한(닫힌 형태) 가로 메르카토르 투영: 횡축 메르카토르: 정확한 솔루션
• 네 번째 순서 간결한 공식에 의한 Redfearn 시리즈(예: 가로 메르카토르: Bowring 시리즈

좌표, 그리드, 동동 및 북향

타원형 횡축 메르카토르의 다양한 발달에 따른 투영 좌표는 중심 자오선이 x축에, 적도는 y축에 해당하는 데카르트 좌표다. x와 y는 모두 λ과 values의 모든 값에 대해 정의된다. 투영은 그리드를 정의하지 않는다: 그리드는 임의로 정의될 수 있는 독립적인 구조물이다. 실제로 국가 구현 및 UTM은 투영의 데카르트 축에 맞춰 정렬된 그리드를 사용하지만, 중심 자오선과 적도 사이의 교차점에는 일치할 필요가 없는 기원을 가진 유한한 범위의 그리드를 사용한다.

진정한 격자 원점은 항상 중심 자오선에서 취하여 격자 좌표가 중심 자오선의 서쪽으로 음이 되게 한다. 그러한 음의 격자 좌표를 피하기 위해, 표준 관행은 격자 원점의 서쪽(그리고 북쪽 또는 남쪽)에 대한 거짓 원점을 정의한다: 거짓 원점에 상대적인 좌표는 항상 양성이 될 동동과 북동을 정의한다. 거짓 동그라미 E는₀ 거짓 원점에서 동쪽에 있는 참 격자 원점의 거리다. 거짓 Northing(N₀)은 거짓 원점에서 북쪽의 참 격자 원점 거리다. 그리드의 실제 기원이 중심 자오선 위도 φ이고₀ 중심 자오선이 k인₀ 경우, 이 정의는 다음과 같이 동동과 북동을 나타낸다.

${\displaystyle {\reasoned}E&=E_{0}+x(\lambda ,\varphi ),\\[5px]N&=N_{0}+y(\lambda ,\varphi )-k_{0}m(\varphi _{0}).\end{정렬}}}$

"동측"과 "북측"이라는 용어는 엄격한 동서남북 방향을 의미하지 않는다. x축과 y축을 제외한 가로 투영의 격자선은 평행과 경맥에 의해 정의된 대로 남북 또는 동서로 흐르지 않는다. 이것은 위에서 보여진 전지구적 예측에서 명백하다. 중심 자오선 부근에서는 차이가 작지만 측정할 수 있다. 남북 격자선과 참된 경맥의 차이는 수렴각이다.

참고 항목

• 지도 투영 목록
• 메르카토르 투영법
• 척도(지도)
• 사선 메르카토르 투영법

참조

외부 링크

• 이 기사를 설명하기 위해 사용된 예상은 http://www.mapthematics.com에서 제공하는 Geocart를 사용하여 작성되었다.