General Perspective 프로젝션

이 기사는 검증을 위해 추가적인 인용이 필요합니다. 신뢰할 수 있는 자료에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. 출처가 밝혀지지 않은 자료에 이의를 제기하여 제거할 수 있습니다.출처 찾기 : "일반적 관점 프로젝션" – 뉴스 · 신문 · 서적 · 학자 · JSTOR (2021년 1월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

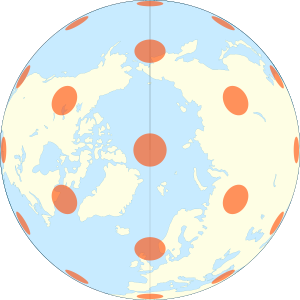
General Perspective 투영은 지도 프로젝션은 지도 프로젝션입니다.지구가 우주에서 촬영되면 카메라는 투시 투영으로 그 모습을 기록합니다.카메라가 지구의 중심을 향할 때 그 결과로 나타나는 투영을 수직 원근법이라고 합니다.다른 방향을 겨냥한 경우 결과 투영을 기울어진 원근법이라고 합니다.

관점과 사용법

수직 원근법은 입체 투영, 지노모닉 투영 및 정사 투영과 관련이 있습니다.이것들은 모두 진정한 관점의 투영이며, 이는 어느 시점에서 지구를 보는 것에서 비롯된다는 것을 의미합니다.이들은 또한 방위각 투영이며, 투영 표면이 구에 접하는 평면임을 의미합니다.그러면 중앙에서 다른 모든 지점으로 정확한 방향이 나타납니다.General Perspective Projection(일반 원근법 투영)의 원근법 시점(vantage point)은 유한한 거리에 있습니다.이 그림은 지표면 위의 비교적 짧은 거리, 일반적으로 몇 백에서 몇 만 킬로미터 정도 떨어진 곳에서 지구가 나타나는 모습을 묘사하고 있습니다.

기울어지면 기울어진 원근법 투영이라고도 하는 일반 원근법 투영은 방위각이 아닙니다(아래 두 번째 그림 참조). 중심점에서 방향이 참이 아니며 투영 평면이 ^[1]구와 접하지 않습니다.기울어진 원근법은 일반적으로 수직 원근법의 전형적인 수백 또는 수천 킬로미터가 아니라 일반적으로 수 킬로미터에서 수 백 킬로미터로 측정된 높이에서 찍은 항공 및 저궤도 사진에서 일반적입니다.하지만, Richard Edes Harrison은 제2차 세계대전 동안 군사 극장을 보여주는 전략 지도에 이 투영을 사용하는 것을 개척했습니다.일부 저명한 인터넷 매핑 도구들도 기울어진 원근법 투영법을 사용합니다.예를 들어, 구글 어스와 나사 월드 윈드는 우주에서 지구의 모습을 보여줍니다.이러한 애플리케이션을 사용하면 비행기나 우주선에서 휴대용 카메라로 찍은 사진이나 영화를 모방하거나 플라이스루 시뮬레이션 등 다양한 대화형 팬과 줌 작업을 할 수 있습니다.

역사

투영의 일부 형태는 2000년 전에 그리스인들과 이집트인들에게 알려져 있었습니다.그것은 18세기와 19세기에 몇몇 프랑스와 영국 과학자들에 의해 연구되었습니다.그러나 당시에는 투영이 실질적인 가치가 거의 없었습니다. 대신 계산적으로 단순한 비원시 방위각 투영법을 사용할 수 있었습니다.

우주 탐험은 원근법 투영에 대한 새로운 관심으로 이어졌습니다.이제 관심사는 왜곡을 최소화하는 것이 아니라 우주에서 바라본 그림을 보는 것이었습니다.우주선의 창문에서 핸드헬드 카메라로 찍은 사진은 기울어진 수직의 원근법을 가지고 있어서, 승무원인 제미니와 아폴로 우주 임무는 이 투영에 대한 관심을 불러일으켰습니다.

수학

일반적인 원근법 투영 공식은 삼각법을 사용하여 유도됩니다.그것들은 구면에서 경도(λ度)와 위도(φ度)로 표기됩니다.구 R의 반지름과 투영의 중심점(및 원점)을₀ 정의합니다(θ, θ₀).(x, y) 접선 평면에 대한 정사 투영 방정식은 ^[2]다음과 같이 줄어듭니다.

${\displaystyle {\begin{aligned}x&=R\,k'\cos \varphi \sin \left(\display -\display _{0}\right)\\y&=R\,k'{\big(}\cos \varphi _{0}\sin \varphi _{0}\cos \varphi \left(\cos -\cos _{0}\right){\big}}\\\end{aligned}}$

어디에

${\displaystyle {\display{aligned}k'&={\frac {d-R}{d-R\cos c}}\\cos c&=\sin \varphi +\cos \varphi _{0}\cos \varphi \left(\display -\cos _{0}\end{aligned}}$

${\displaystyle }$c$${\$displaystyle$ c$}$는 각도 거리이고 $d{\displaystyle }${\$displaystyle$ d$}$는 원근점에서 지구 중심까지의 거리를 ${\displaystyle \mathrm{나타냅니다}}$.투영의 중심 방향("공간에서 보는 뷰"의 경우)에서는 양수이고 반대 방향에서는 음수입니다.입체 투영의 경우 d = - ${\displaystyle R}$ ${\displaystyle$ d=-$R$이고, 그로노닉 투영의 경우 d = ${\displaystyle 0}${\$displaystyle$ d=$0$입니다.

역 공식은 다음과 같이 제공됩니다.

${\displaystyle {\display{aligned}\phi &=\arcsin \left(\cos c\sin \phi _{0}+{\frac {y}{\rho}}}\sin c\cos \phi _{0}+\arctan \left)\displaystyle {\cos {\display{aligned}\pi &=\displaystyle {\cos {{0}-y\sin c\right)\end{aligned}}$

어디에

${\displaystyle {\display{aligned}\rho &={\sqrt {x^{2}+y^{2}}}}\c&=\arcsin {\frac {P-{\sqrt {1-{\frac {\rho ^{2}(P+1)}{R^{2}(P-1)}}}}{{\frac {R(P-1)}}{{\rho}}}}}{{\frac {\rho}}}}}}\end{aligned}}}$

$P$ ${\displaystyle$ P$}$가 음수이고$$ρ {\$displaystyle \rho}$가 R${\displaystyle (P}$- ${\displaystyle 1)}$ / ${\displaystyle P}$ ${\displaystyle$ R$(P-1)/P$보다 크면 $적절한$ 사분면에 배치하려면 180°에서 c$${\$displaystyle$ c$}$을(를) 빼야 합니다.역 공식을 계산하려면 역 탄젠트 함수의 2 형태(아탄과 반대)에서 2개의 인수를 사용하는 것이 좋습니다.이렇게 하면 모든 사분면에서 작성된 직교 투영의 부호가 정확합니다.

참고 항목

• 지도 투영도 목록
• 지도투영

참고문헌